基于小波PWM调制的逆变器特性分析

郑春芳 米志红 张 波 丘东元 张晓慧

基于小波PWM调制的逆变器特性分析

郑春芳1米志红1张 波2丘东元2张晓慧2

（1. 广州航海学院 广州510515 2. 华南理工大学 广州 510640）

本文介绍了基于非二进制离散小波分辨率分析的小波PWM调制原理和实现方法，分析并给出了小波PWM调制中不同参数对逆变器输出性能的影响，有利于选择合理的参数。并利用谐波消除的原理，通过具体算例将小波PWM调制与SPWM技术进行比较，仿真和实验结果表明，小波PWM调制具有数字化算法实现更简单，电压利用率更高，谐波总畸变率（THD）更小的优点，但是输出电压调节范围更小以及对低次谐波的抑制能力更差，为小波PWM调制更有效的实际应用提供了理论依据。

逆变器 小波调制 SPWM

1 引言

PWM控制技术是逆变器研究和应用领域的核心技术之一，它的发展经历了一个不断进步和完善的过程，目前已经提出并得到实际应用的PWM控制方案就不下十几种[1-5]，主要可以分为四大类即载波调制PWM技术、特定谐波消除PWM技术、空间矢量PWM技术、随机PWM技术。寻求最优的PWM控制模式，力求降低逆变器输出中的谐波分量，提高逆变器输出性能，仍然是国内外学者研究的主要努力方向。近年来，加拿大学者S.A.Saleh学者在用逆变器小波PWM调制方面做了积极的探索[6-10]，于2006年在文献[6]中首次提出利用小波PWM调制（Wavelet PWM modulation，简称WM）技术来产生逆变器开关的控制信号，通过实验得出这种基于非二进制离散小波分辨率分析的控制策略具有数字化算法实现更简单，逆变器的电压利用率更高，谐波总畸变率（THD）更小的优点，从而证明了小波PWM调制在电力电子变换器中的应用是可行的。

本文在介绍小波PWM调制的原理和实现方法的基础上，主要分析小波PWM调制不同参数对逆变器输出电压利用率、谐波总畸变率（THD）以及各次谐波抑制能力等的影响，并利用谐波消除的原理，通过具体算例与SPWM技术进行比较，从理论上全面地显示出小波PWM调制的优缺点，有助于探讨小波PWM调制在实际应用中的可行性。最后通过实验验证了小波PWM调制技术理论分析的正确性。

2 小波PWM调制技术的原理和算法

基于二进制离散小波多分辨率分析的小波PWM调制是用多组采样和合成基函数组成的非均匀循环方式去采样-重组参考调制信号。采样基函数是由线性组合尺度函数φ（j,k)(t)经过伸缩和平移产生的。而且合成基函数是由线性组合合成尺度函数φ˜(j,k)(t)经过伸缩和平移产生的。在尺度j下的线性合成尺度函数定义为:

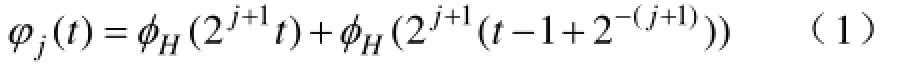
期中j=0,1,2,3,…; φH(t)是Harr尺度函数其表达式如下:

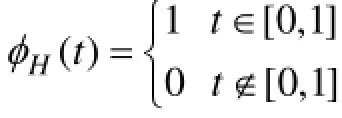
而且合成尺度函数()tφ˜与φ(t)函数之间的关系可以定义为:

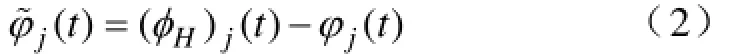
利用这两组尺度函数，连续时间信号xc(t)可以扩展为:

期中j, k为整数。这种形式的信号处理过程意味着一个连续时间信号可以从由用一组合成函数得到的采样点中恢复。

图1是j=0,1,2，k=0,1,2时的尺度函数φ(t)与φ˜(t )的图示。

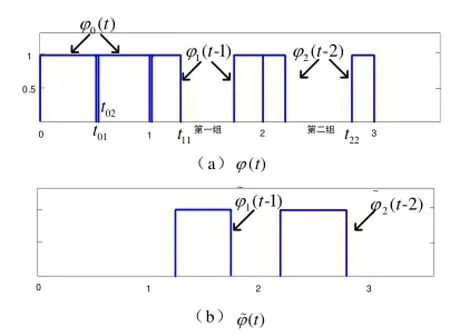
图1 j=0,1,2，k=0,1,2时的尺度函数φ(t)与()tφ˜Fig.1 Scaling functions φ(t) and ()tφ˜for j=0,1,2, k=0,1,2

如果连续时间信号xc(t)≠0，则〈xc(t)，φ1,k(t)〉的内积不为0，φj(t)对于特定的伸缩（改变j）与平移（改变k），能得到一组采样点。对xc(t)，在一周内总的采样组数是有限的，令其为D，每一组可以表示为[td1,td2]，则:

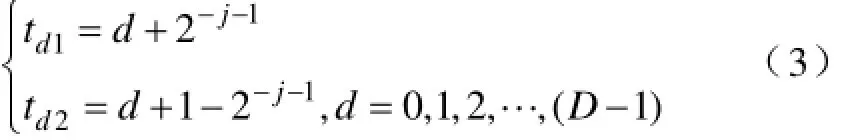
文献[6]根据拉格朗日插值原理证明了由尺度函数φˆj(t)经过平移和伸缩正好可以代替得到驱动开关器件，即将每组采样点[td1,td2]做为开关驱动脉冲的脉宽，它们是一系列的脉宽不等的脉冲，这样就得到了逆变器所需的开关驱动脉冲。从而，可以用φ(t)通过不同的尺度j产生不同的开关脉冲，通过这些不同宽度的脉冲来重新得到连续信号。

对于DC/AC逆变器，被采样的信号是正弦信号，它具有四分之一周期对称的特性。这个特性使得尺度j在区间是逐渐增加的，在

是逐渐减小的（mT是正弦信号的周期）。

因此，基于二进制离散小波多分辨率分析过程的小波PWM调制的计算步骤有:

（1）设定尺度参数j的初始值0j，并且采样组序d的初始值0d；

（2）设定一个采样点为td1=d+2-j-1，另一个采样点位t=d+1-2-j-1；d2区间

（3）在上述两个采样点内形成一个开关脉冲；

（5）如果t≥Tm，则j=j0，d=d0，否则d=d+1；

（6）返回第2步，重新计算。

图2是单相全桥逆变器的原理图，当Q1Q3闭合时，Q2Q4断开；当Q1Q3断开时，Q2Q4闭合。对于图3中的单相逆变器，取D=30、fm=50Hz、按照图2的流程图，图2中的Tst为采样频率，取Tst=1μs，利用Matlab中的Simulink可得到其Q1Q3和Q2Q4的小波PWM调制信号波形[11]，如图3所示。

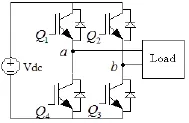
图2 单相全桥逆变器主电路Fig.2 Main circuit of a single-phase full-bridge inverter

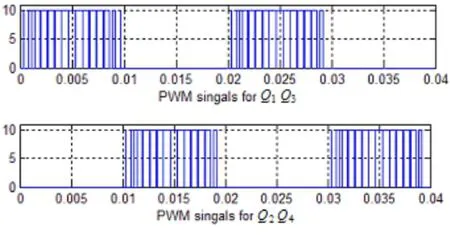
图3 D=30时Q1Q3和Q2Q4的小波PWM调制信号波形Fig.3 WPWM signal waveforms for Q1Q3and Q2Q4at D=30

3 小波PWM调制对逆变器特性的影响

逆变器输出电压波形主要取决于尺度参数j和一周内总的采样组数D。下面从电压基波幅值（即调制比或电压利用率）和总谐波电压畸变率两个方面来考查尺度参数j 和D对逆变器输出电压的响。

将每个采样组内计算得到的采样点td1，td2转换为开关角度αi,i =1,2,3,…,D ，如图4所示。

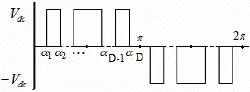
图4 单极性控制逆变器输出电压波形Fig.4 Output voltage waveform of unipolar-controlled inverters

对图5进行傅立叶分析，可得单极性单相逆变器的非线性模型为[12]

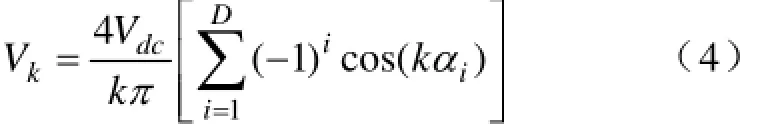
其中第kth次谐波幅值，…,7,5,3,1=k；1V为基波幅值；逆变器的调制比（或电压利用率）定义为:某次谐波抑制能力和总谐波电压畸变率THD分别定义为[13]:

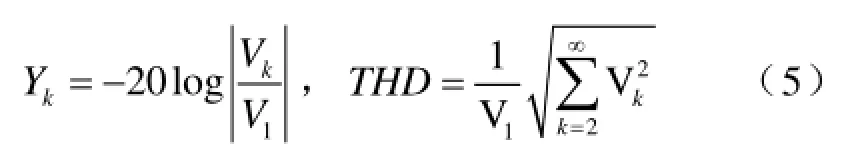
本文以频率为50Hz的正弦波为采样对象，采样组系数D从10一直到50，根据式（4）和式（5），计算出单相逆变器在不同尺度参数初始值j0=0,1,2,3下的总谐波电压畸变率THD（注:取所有前101次奇次谐波），得到THD在j0=0,1,2,3的变化情况如图5所示和逆变器调制比m在j0=0,1,2,3的变化情况如图6所示。从图5中可以看出:（1）j0＝0时在D≥20，其 THD都是最小的；（2）在同一j0值下，在D＞30后THD数值基本上变化很小；（3）在j0＞3后，不同的D值下， THD值变化很小。从图6中可以看出:（1）逆变器调制比m随着D的增大而增大，在j0=0时，m从0.6195增大到1.2149；（2）在D≥20，m＞1；（3）在同一 D值下，m随着j0的增大而增大，当j0＞7时，m接近 1.2732（此时的脉冲波形基本为方波）。（4）随着D值的增大，m可以调节的范围变小。

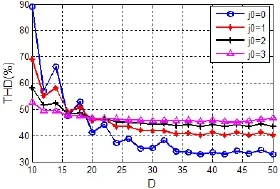
图5 j0=0,1,2,3时THD随D的变化规律Fig.5 THD vs.D of j0=0, 1, 2, 3

为了更详细地了解在不同D和j0下，单相逆变器小波PWM调制的输出特性，图7（见附录）分别给出了D=20,30,40,50下j0=0,1,2,3时逆变器的前40次谐波抑制能力。从图7综合来看，小波PWM调制在j0=0下对低次谐波的抑制能力更好些。

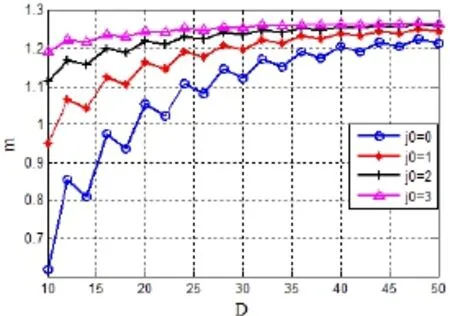
图6 j0=0,1,2,3时m随D的变化规律Fig.6 m vs.D of j0=0, 1, 2, 3

4 小波PWM调制与SPWM特性比较

文献[14]给出了自然采样单极性SPWM开关点方程分别表示为:

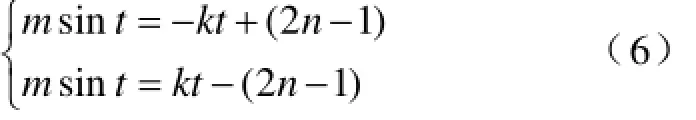
其中n=1,2,…,N ；k=2N/π；m=Urm/Ucm为调制比；Urm为正弦调制波峰值；Ucm三角载波峰值；Tc为载波周期；N为载波比，Tc=π/N。

为了将小波PWM调制与SPWM技术进行比较，需满足:单位周期内的脉冲数相等。根据小波PWM调制原理及SPWM的原理，可知这两种调制方法在单位周期内的脉冲数相等的条件是:小波PWM调制的采样组系数D与SPWM的载波比N的两倍，即D=2×N 。

本节首先根据第3节介绍的小波PWM调制算法计算出在j0=0，采样组数D=20、30、40、50下的各开关点数值。然后用常规的牛顿迭代法求解SPWM开关点方程（式（6）），迭代误差取小于1e-6（将迭代误差取得更小，则开关点就更加接近精确值），计算得到开关点的近似值。最后根据式（4）和式（5）得到其对应的THD和各次谐波抑制能力。对应的THD和调制比m的计算结果见表1中。对应的各次谐波抑制能力如图8（见附录）所示。从表1中可看出:小波PWM调制具有调制比更高和总谐波畸变率更低的优势。但从图8中可看出:小波PWM调制对低次谐波的抑制能力远远比不上SPWM技术。

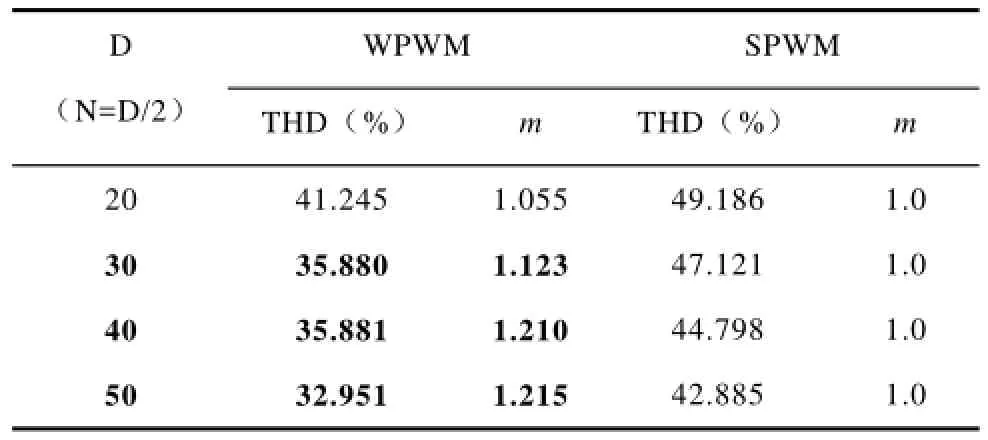
表1 小波PWM调制和SPWM技术比较结果Tab.1 The comparison results between WSPWM and SPWM

为了验证表1中算例的正确性，本文分别用小波PWM调制和SPWM技术去控制单相逆变器（见图3），取基频fm=50Hz，D=30（对小波PWM）；N=15，m=1.0（对SPWM），利用Matlab软件中的Simulink进行建模仿真，可得到其输出电压波形Uab及傅里叶频谱分析结果分别如图9a、9b所示。由图9和表1对照可知，两种分析结果基本一致，从而验证了理论分析的正确性。

因此，在实际应用小波PWM调制时，要综合考虑逆变器输出性能要求和应用场合，选择合适的采样组数D。

5 实验结果

为了验证小波PWM调制技术控制单相全桥逆变器的实际性能，本文采用DSP（TMS320LF2812）作为控制器完成小波PWM调制的算法（算法中选择j0=0, D=30、40, fm=50Hz）分别在线计算出开关点，TLP250作驱动，开关管选Mosfet IRF830，输入电压Vdc=50V ，纯电阻作负载进行实验。单相逆变器的输出电压及其频谱的实验结果如图10a、10b所示，从图中读出输出电压基波有效值分别为39.8V和43V，和小波PWM技术分别在D=30和D=40时输出电压基波的理论值50Vdc*1.123/2=39.7Vdc和50Vdc*1.210/=42.8Vdc基本一致。

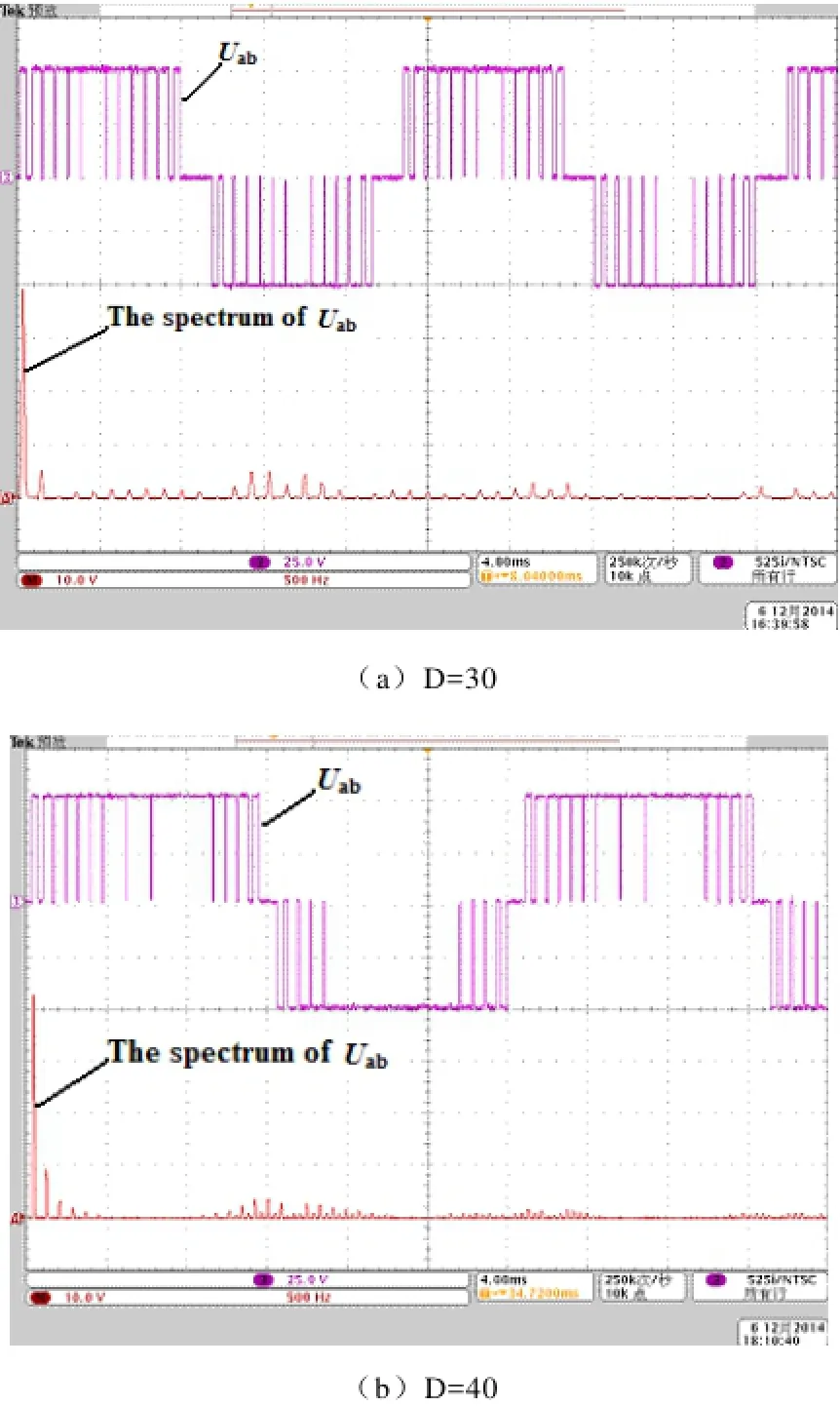
图10 WPWM控制下在j0=0, D=30/40时单相逆变器的输出电压及其频谱Fig.10 Output voltage and its spectrum for single-phase inverters controlled by WPWM at j0=0, D=30/40, fm=50Hz

6 结论

本文在介绍小波PWM调制的原理和实现方法的基础上，分析了小波PWM调制中不同参数对逆变器输出性能的影响，并通过具体算例与SPWM技术进行比较，计算仿真和实验的结果都表明:

（1）小波PWM调制在尺度参数初始值j0=0下对低次谐波的抑制能力更好些。

（2）小波PWM调制在j0=0，D≥20下，调制比m＞1。

（3）与SPWM技术相比，具有数字化实现更简单，电压利用率更高，谐波总畸变率（THD）更小的优点，但是输出电压调节范围更小以及对低次谐波的抑制能力更差。

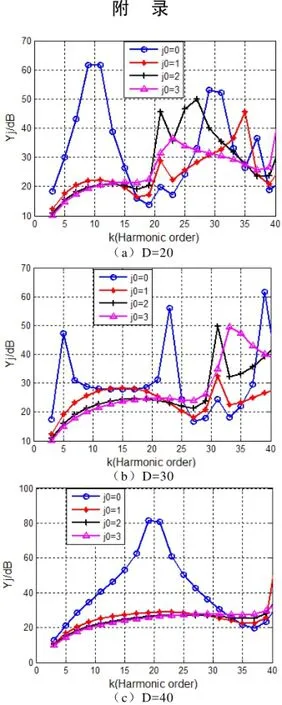
图7 D=20,30,40时小波PWM调制在j0=0,1,2,3下的各次谐波抑制能力Fig.7 The ability of eliminating harmonics for WPWM at j0=0,1,2,3 when D =20,30,40

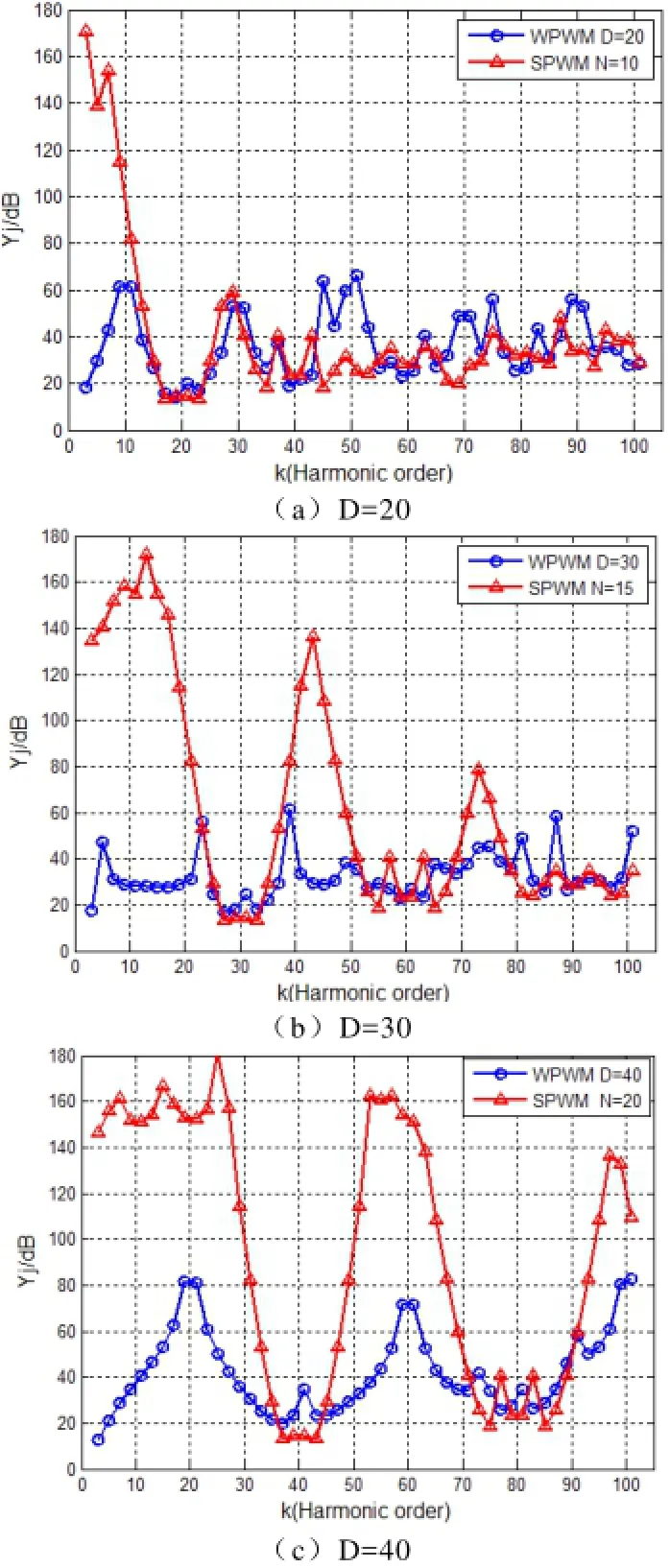
图8 D=20,30,40下小波PWM调制和SPWM的各次谐波抑制能力Fig.8 The ability of eliminating harmonics for WPWM at j0=0 when D=20, 30, 40 and SPWM

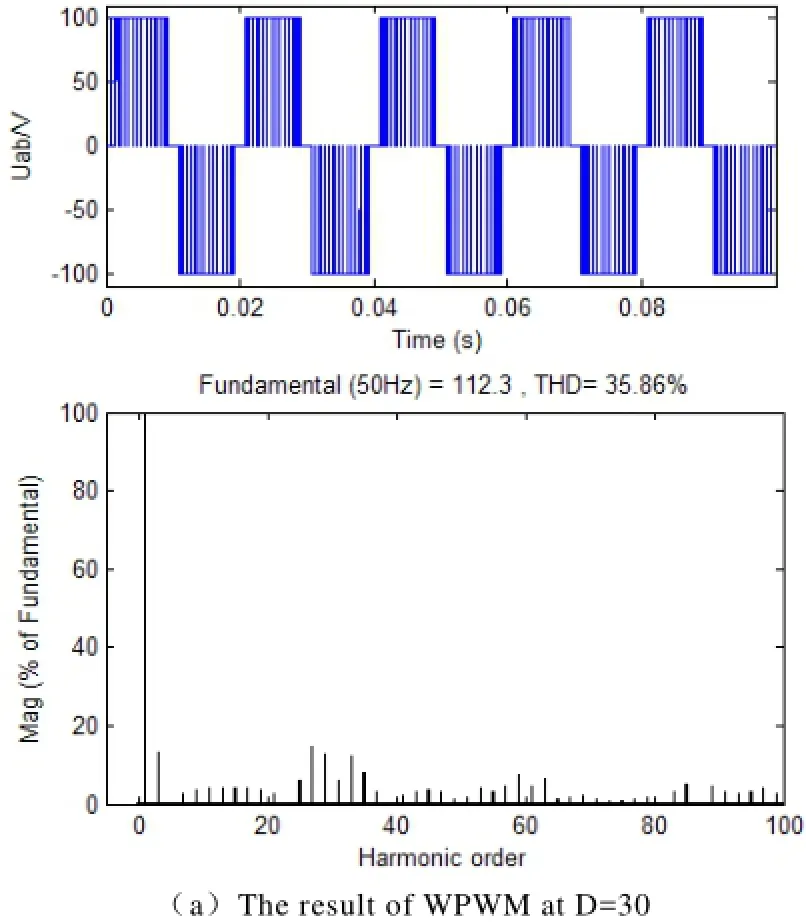
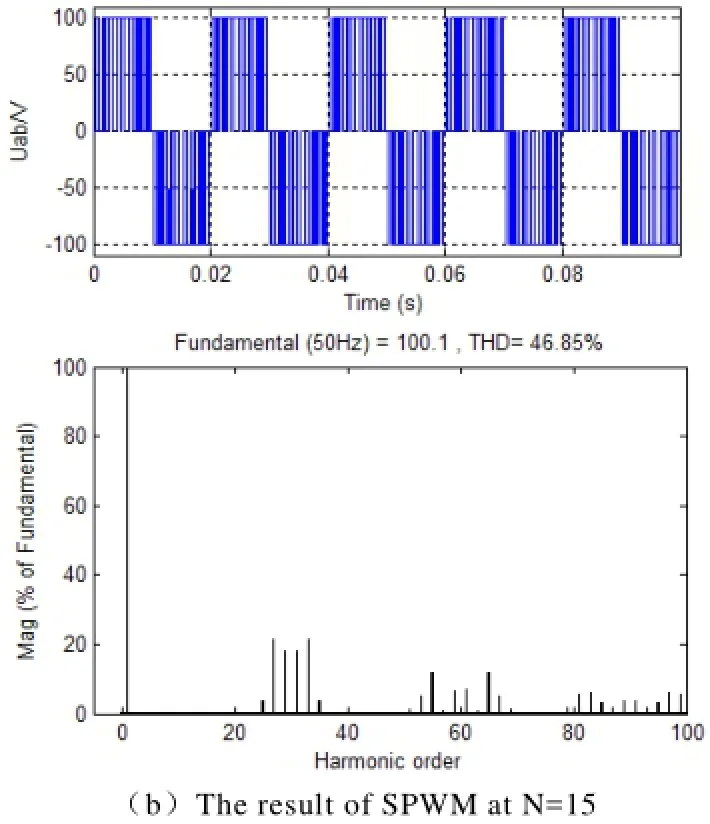
图9 D=30/N=15时在小波PWM调制和SPWM控制的单相全桥逆变器的输出电压Uab及其频谱Fig.9 Output voltage Uab and its spectrum for single-phase FB inverters controlled by WPWM and SPWM at D=30/N=15

[1] Sidney R Bowes. Simple microprocessor implementation of new regular- sampled harmonic elimination technique[J]. IEEE Trans. on Ind. Applica. , 28(1), 1992: 89-95.

[2] Chaudhari B N, Femandes B G. EPROM-based modulator for synchronized asymmetric regularsampled SPWM technique[C]. Industrial Technology 2000 Proceedings of IEEE International Conference on, 2(1), 2000: 278-283.

[3] Chiasson, L M Tolbert, K McKenzie. A complete solution to the harmonic elimination problem [J]. IEEE Trans. On Power Electronics, 19(2), 2004: 491-499.

[4] 孟超, 欧阳红林等. 双Y 移30。永磁同步电机的空间矢量调制[J]. 中国电机工程学报, 2010, 30(3): 90-99.

MENG Chao. OUYANG Honglin，etc. Space-vector PWM technique for Dual Y shift 30 degree Permanent-magnet synchronous motor[J]. Proceedings of the CSEE, 2010, 30(3): 90-99.

[5] Hamidkhan, El-Hadj Miliani, Hichame Ouzaarou, et al. Random Discontinuous Space Vector Modulation for variable speed drives[J]. IEEE Transactions on Power Electronics, 2012: 4944-4951.

[6] S. A. Saleh, C. R. Moloney, and M. A. Rahman. developing a nondyadic MRAS for switching DCAC inverters[C]. in Proc. IEEE 12th DSP Conf, Jackson Lake Lodge, WY, 2006: 544-549.

[7] S. A. Saleh, C. R. Moloney and M. A. Rahman. Development and Testing of Wavelet Modulation for Single-Phase Inverters[J]．IEEE Trans. on Industrial Electronics, 2009, 56(7): 2588-2599.

[8] S. A. Saleh, C. R. Moloney, and M. A. Rahman. Analysis and Development of Wavelet Modulation for Three Phase Voltage Source Inverters[J]. IEEE Trans. on Industrial Electronics, 2010, 99: 1-19.

[9] S A. Saleh. Resolution-Level-Controlled WM Inverter for PMG-based wind energy conversion system[J]. IEEE Transactions on Industrial Electronics, 2012, 48(2): 750-63.

[10] S. A. Saleh. The implementation and performance evaluation of three-phase VS wavelet modulated AC-DC converters[J]. IEEE Transactions on Power Delivery, 2013, 28(3): 1096-1106.

[11] 葛哲学, 沙威．小波分析理论与MATLABR2007实现[M]．北京: 电子工业出版社, 2007.

GE Zhexue, SHA Wei. The wavelet analysis theory and realization by MATLAB2007[M]. Beijing: the Electronic industry press, 2007.

[12] 郑春芳, 张波．吴方法在电力电子逆变器消谐技术中的应用[J]．中国电机工程学报, 2005, 25（15）: 40-45.

Zheng Chunfang, Zhang Bo. Application of wu method to harmonic elimination techniques[J], Proceedings of the CSEE, 2005, 25(15): 40-45.

[13] 钟福金，钱昱明，王晓军. 交流变频调速系统的SPWM波形生成方法的谐波分析[J]. 南京航空航天大学学报, 第26卷增刊, 1994: 94-98.

Zhong Fujin; Qian Yuming;Wang Xiaojun. Harmornic Analysis of methods forming SPWM wave in VVVF system[J]. Transactions of NanJing University of Aeronautics, 1994: 94-98.

[14] Zheng Chunfang, Zhang Bo, Qiu Dongyuan.Digital Natural Sampling SPWM based on Inverse Operator Method, PESC 2007, June 2007, Orlando, Florida, USA: 792-797.

Inverter’s Characteristic Analysis Based on the Wavelet PWM Modulation

Zheng Chunfang1 Mi Zhihong1 Zhang Bo2 Qiu Dongyuan2 Zhang Xiaohui2
（1. Guangzhou Maritime Institute Guangzhou 510515 China; 2. South China University of Technology Guangzhou 510640 China）

This paper presents the principle and implementation of the wavelet PWM（WPWM）technique based on dyadic-type multi-resolution analyses (MRAs) for single-phase inverters, analyzes and gives the inverter’s output features at different parameters based on WPWM technique, which is beneficial to choose suitable parameters. Then, according to the harmonic eliminating principle, compares WPWM with SPWM technique by some specific examples. The simulation and experimental results show that WPWM can get simpler realization by digital algorithm, higher fundamental component magnitudes and lower THD factors, but the range of fundamental component magnitude is smaller and the ability of eliminating lower harmonics is worse, which provide theoretical basis for the application of the WPWM efficiently in practice.

Inverters, Wavelet Modulation, SPWM

TM464

郑春芳 女，1978年出生，博士，从事电力电子及电力传动技术的研究。

国家自然科学基金重点项目（51437005）和国家自然科学基金项目（51277079）。

2015-03-25 改稿日期 2015-06-09

米志红 女，1971年出生，硕士，从事电力电子及电力传动技术的研究。