基于灰色系统理论的河南省科技进步贡献率测算
张汴生,陈东照
(1.河南省科学技术发展战略研究所,河南 郑州450008;2.河南机电职业学院,河南新郑451191)
科技进步贡献率是衡量区域科技竞争实力和科技转化为现实生产力的综合性指标,反映了科学与技术对社会经济发展的作用效果。很多学者对科技进步贡献率的测算进行了研究,并取得了不少的研究成果。国外的科技进步测定模型主要有4种:SOLOW[1]于1957提出的索洛余值法;ARROW等[2]于1961年提出的常数替代弹性(CES)生产函数;CHRISTENSEN等[3]于1973年共同提出的超越对数生产函数;DENISON[4]于1975年提出的丹尼森增长因素分析法。国内杨少华等[5]在采用索洛模型测算中国的科技进步贡献率时,把劳动、资本的产出弹性作为一个动态指标来测算;鲁亚运[6]通过构建时滞灰色生产函数,并利用灰色关联度确定时滞阶数,对生产函数的指标值进行准确的衡量;李泽星[7]和李莲靖[8]分别运用索洛余值法对辽宁省和广西省的科技进步贡献率进行了测算。这些研究成果为科学地测算科技进步贡献率提供了理论支持。但是,已有研究成果大多是把资本和劳动投入增长以外的其它因素对产出的贡献都归结到“技术进步”中,很少考虑到技术进步因素具有不确定性,这样处理不尽合理。灰色系统理论适合于解决小样本、贫信息的不确定性问题,本研究充分考虑技术进步因素的不确定性,运用灰色系统理论研究具有丰富内涵的科技进步“余值”,在确立数据收集及处理规范的基础上,建立灰色生产函数模型(G-C-D模型),进而弱化索洛余值中的非技术进步因素,试图在一定程度上提高技术进步贡献率测度的合理性。
1 灰色C-D生产函数模型
Cobb-Douglas生产函数模型的形式为

式中:Y为产出,A0为常数,r为技术进步系数,K为资本投入,L为劳动力投入,α为资本弹性,β为劳动力弹性,假设规模报酬不变,即α+β=1。
将(1)式两边同时取对数,得到
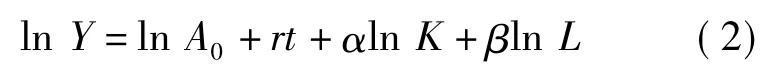
由于α+β=1,上式可变形为
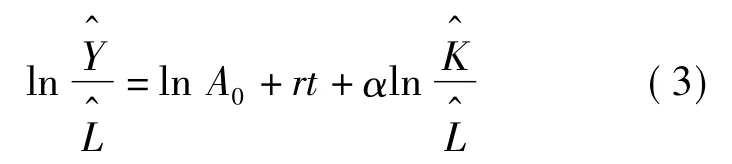
以产出Y,资本K和劳动力L为时间序列数据,对式(3)采用最小二乘原理计算出参数 A0、r、α、β。
然后采用索洛余值法可计算出技术进步速度

在基于数据进行系统行为的量化分析时,选择适当的方式解决系统的特征数据因受冲击因素干扰导致的失真问题是至关重要的。缓冲算子是灰色系统理论中克服冲击扰动系统行为数据序列影响的核心工具,它能克服冲击扰动影响,挖掘数据规律,有效地解决冲击扰动数据序列在建模预测过程中出现的定量预测与定性分析结论不符的问题。
选取适当的缓冲算子,弱化冲击扰动项对原始序列的影响,再利用GM(1,1)模型进行模拟,得到模拟序列
由此序列可得出产出与资本、劳动力和技术进步的关系,则称

为灰色生产函数模型。
由式(5)所得结果代入式(4)可求出技术进步对产出增长速度的贡献份额
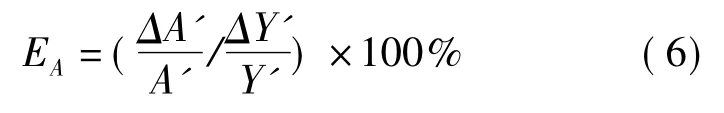
EA通常称为技术进步对经济增长速度的贡献率,简称科技进步贡献率,同理可以求出资本和劳动力对产出增长速度的贡献率EK和EL。


2 河南省科技进步贡献率的测算
2.1 数据选取
2.1.1 产出Y 产出一般用国内生产总值(GDP)来衡量。将当年价格换算为不变价格来反映生产活动成果的实际变动,考虑到数据的可操作性,最终选取以2000年为基准年。采用GDP指数将现价GDP换算为不变价格GDP,具体公式如下:GDP指数按上年等于100的可比价格计算。

2.1.2 劳动力L 理论上的劳动投入量是指实际投入的劳动量,其不仅取决于劳动的投入数量,还与劳动的利用效率、劳动者素质有关。基于实际的可操作性,本研究选用全社会从业人数作为劳动投入量的统计指标。
2.1.3 资本K 理论上,以某年的固定资产净值加该年的定额流动资金年平均余额作为这一年的资本投入量是比较合理的,由于中国没有大规模的资产普查,因此本文采用戈登史密斯(Goldsmith)在1951年开创的永续盘存法来估算当年的资本存量,计算公式为:

式中:Kt为t时期(这里为年)修正后的固定资本存量净值;It为t时期的固定资本投资额;Pt为第t期的固定资产投资价格指数,同样,将资本投入量也换算成2000年不变价数值。δ为固定资产折旧率:在折旧率的选择上,各个研究有较大的出入。本研究的经济折旧率使用张军等[9]计算得到的9.6%。
基年固定资本形成存量K0的估计:这一数据的取得采用国际常用计算方法:K0=I0/(g+δ)。其中,δ是折旧率,I0是基期的固定资本投资额,g是样本期真实投资的年平均增长率,计算公式如下:

式中:It为计算期t年的固定资本投资额;I0为基期的固定资本投资额;n为计算期和基年的间隔年份。
2.2 科技进步贡献率的测算
选取2000—2013年河南省国内生产总值、就业人数、资本存量等面板数据进行研究。考虑数据的波动性和不确定性,首先采用缓冲算子对原始数据进行处理,再利用GM(1,1)模型进行模拟,使索洛余值法计算出的技术进步更加接近实际。河南省G-C-D生产函数模型的对数形式为

利用式(12)中得到弹性系数α、β的取值,运用式(6)、(7)、(8),分别得到2000—2013年河南省1年期、5年期科技进步对产出增长速度的贡献份额EA、资本和劳动力对产出增长速度的贡献率EK和EL,结果见表1和表2。
有文献显示,资本弹性系数α取值介于0.2至0.3之间较为合理[10]。为避免建模偏差导致“余值”测算误差,对α进行适度拓展,分别取α=0.2,0.3,由式(3)和式(6)计算相应的科技进步贡献率。对2组数值进行加权平均,用处理的数值对G-C-D模型科技进步贡献率进行修正。
综合表1、表2中的科技进步贡献率和表3、表4中的科技进步贡献率,可得各科技进步贡献率灰朦胧集的取数域及其均值白化数,见表5、表6。
从表1和表2测算结果可知,在2001—2013年无论是1年期还是5年期的测算,河南省资本投入对经济增长的平均贡献率均高于科技进步对经济增长的平均贡献率,而劳动投入对经济增长的平均贡献率都是最低的。由此可见,2001年以来,推动河南经济增长的主要动力是资本投入,其次是科技投入,劳动投入的作用最小。从表5可以看出,河南省2000—2013年1年期科技进步贡献率在38% ~48%之间,总体呈上升的趋势,局部稍有波动,2013年达到最高47.76%。从表6可以看出,河南省2000—2013年5年期科技进步贡献率基本在25% ~51%之间,总体呈上升趋势,由于2008年金融危机的影响,跨越2008年的时段科技贡献率的增幅放慢,2009—2013年达到最高50.99%。
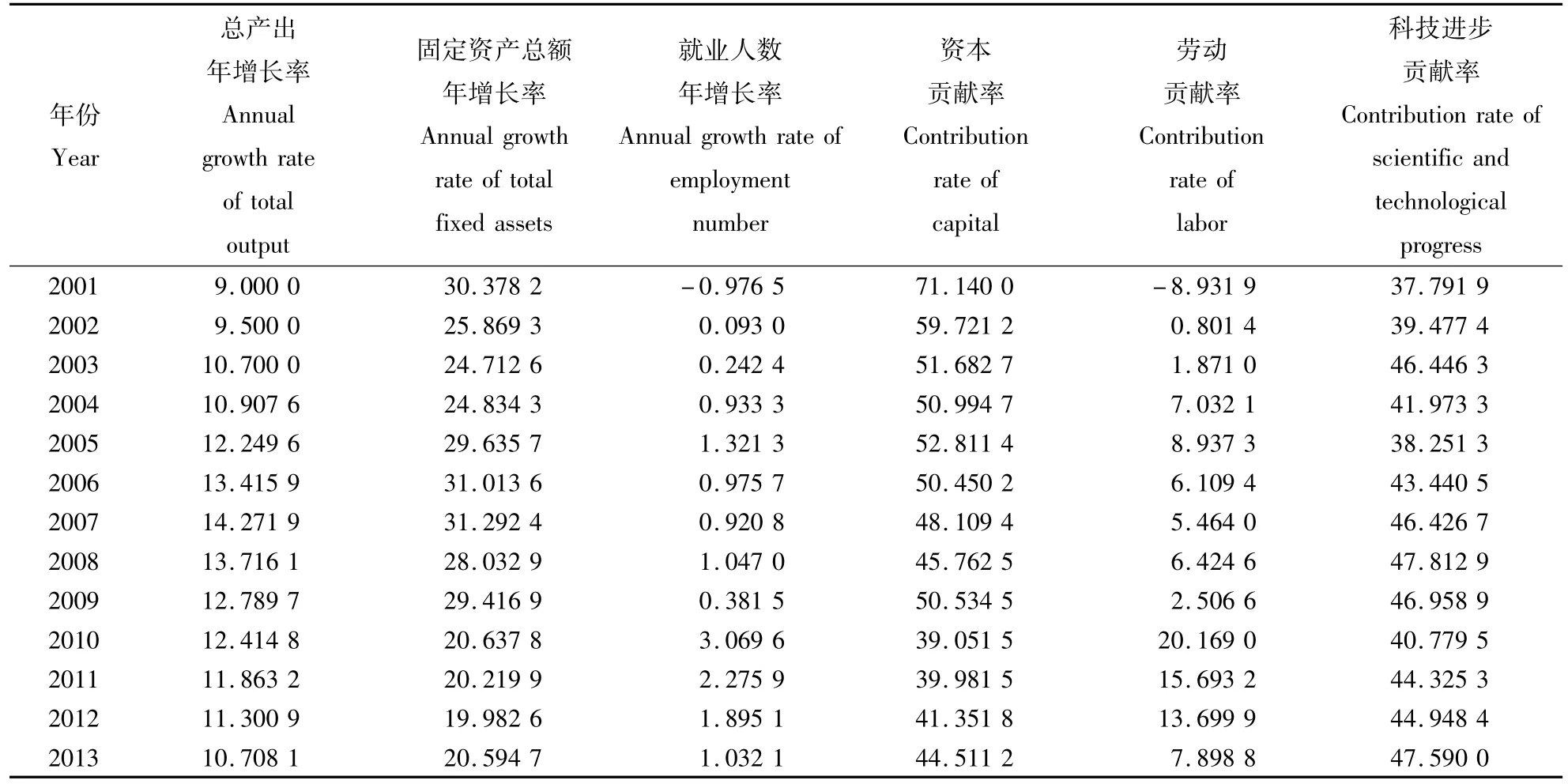
表1 基于G-C-D模型的1年期各生产要素年增长率和贡献率Table 1 Annual growth rate and contribution rate of each production factor in 1 year based on Model G-C-D %

表2 基于G-C-D模型的5年期各生产要素年增长率和贡献率Table 2 Annual growth rate and contribution rate of each production factor in 5 years based on Model G-C-D %

表 3 α =0.2,0.3;β =0.8,0.7 1 年期科技进步贡献率Table 3 α =0.2,0.3;β =0.8,0.7 Contribution rate of scientific and technological progress in 1 year %
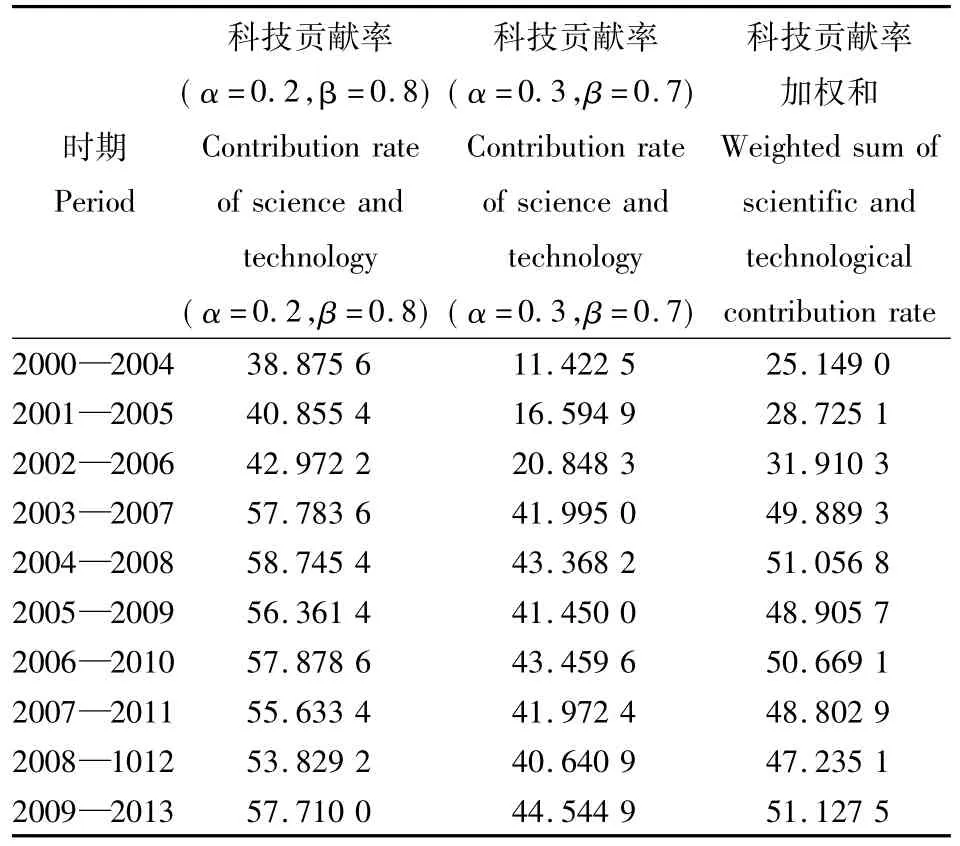
表4 α=0.2,0.3;β =0.8,0.7 5 年期科技进步贡献率Table 4 α =0.2,0.3;β =0.8,0.7 Contribution rate of scientific and technological progress in 5 years %

表5 河南省2000—2013年1年期科技进步贡献率Table 5 Contribution rate of scientific and technological progress in Henan Province 2000 to 2013 one-year%

表6 河南省2000—2013年5年期科技进步贡献率Table 6 Contribution rate of scientific and technological progress in Henan Province 2000 to 2013 five-year%
3 结论
本研究为弱化索洛余值中的非技术进步因素,运用灰色系统理论的基本原理,将灰色系统理论的思想方法和模型技术相结合,建立了灰色柯布-道格拉斯生产函数模型。运用该方法对河南省2000—2013年的科技进步贡献率进行测算。测算结果表明:河南省科技进步贡献率总体呈上升趋势,并具有阶段性特征,同时也体现了河南省经济增长还处于主要依靠大量要素投入支撑的经济增长方式阶段。从长远来看,河南省实现经济持续、健康发展,加大科技投入,依靠技术进步的力量,推进河南省经济增长是极其必要的。
科技对经济增长的贡献具有滞后性、长期性和一定的周期性。科技进步贡献率测算依据的是数学模型,易受经济增长率、资本增长率和劳动力增长率3个统计数据的影响。特别是短期内受科技进步滞后特性以及数学模型局限性的影响,当经济剧烈波动时,模型的短期测算结果往往失真。科技进步贡献率测算以中长期为主,才能取得较理想的效果。
[1] SOLOW R M.Technical change and the aggregate production function[J].The Review of Economics and Statistics,1957:39:312-320.
[2] ARROW K J,CHENERY H B,MINHAS B S,et al.Capital-Labor substitution and economic efficiency[J].The Review of Economics and Statistics,1961,43(3):225-250.
[3] CHRISTENSEN L R,JORGENSON D W,LAU L J.Transcendental logarithmic production frontiers[J].Review of Economics and Statistics,1973,55:28-45.
[4] DENISON E F.Accounting for United States Economic Growth,1929 to 1969 [J].The Economic Journal,1975,85:410-412.
[5] 杨少华,郑 伟.科技进步贡献率测算方法的改进[J].统计与决策,2011(8):22-24.
[6] 鲁亚运.基于时滞灰色生产函数的我国海洋科技进步贡献率研究[J],科技管理研究,2014(12):55-59.
[7] 李泽星.辽宁省科技进步贡献率的分析与测算[J].科技经济市场,2014(5):93-95.
[8] 李莲靖.广西科技进步贡献率测算与分析:1978—2010[J].经济研究导刊,2014(21):74-76.
[9] 张 军,吴桂英,张吉鹏.中国省际物质资本存量估算:1952—2000[J].经济研究,2004(10):35-44.
[10] 史清琪,秦宝庭,陈 警.技术进步与经济增长[M].北京:科学技术文献出版社,1985.

