河南省生态环境与经济增长关系的动态计量分析
范慧平,孟天醒,文 倩,宋文博
(河南农业大学资源与环境学院,河南郑州450002)
国外学者对经济增长与生态环境的关系研究较早。1995年美国环境经济学家 GROSSMAN等[1]以78个发达国家的面板数据采用计量经济学方法进行实证分析,结果显示,城市生态环境质量随经济水平提高呈倒“U”型演变,并提出著名的环境库兹涅茨曲线(EKC)假设。PANAYOTOU等[2]以及COPELAND等[3]分别将环境质量和环境服务看作商品,再次验证了库兹涅茨曲线即环境质量需求的收入弹性随经济收入的增加逐渐提高,当收入弹性大于1时,人们会为改善环境质量而舍弃经济利益。吴开亚等[4]、沈满洪等[5]及邢秀凤等[6]研究所得出的EKC曲线不完全符合典型的库兹涅茨假设,而呈“倒U+U”型的三次曲线形状。王长建等[7]采用熵值支持下的AHP法对新疆城市化与生态环境关系研究显示,生态环境质量指数和响应指数随城市化水平提升先下降后上升。周玄德等[8]采用协调度模型分析克拉玛依市经济增长与生态环境的关系,该市经济和生态环境均呈上升趋势,但经济增长明显快于环境改善,二者耦合协调度随时间序列整体呈增长趋势,但不绝对稳定。由于中国的工业化模式基本沿袭了发达国家“先污染后治理”的道路。因此,研究经济与环境的协调发展,对制定区域发展规划与生态环境保护措施具有重要意义。本研究采用BP神经网络与计量经济模型研究河南省经济增长与生态环境的关系,为促进经济健康发展、资源合理开发利用、生态环境保护、新型城镇化建设、以及国家粮食安全与区域可持续发展提供理论和实践指导。
1 研究区概况与数据来源
1.1 研究区概况
河南省位于中国中东部、黄河中下游,位于北纬 31°23'~36°22'、东经 110°21'~116°39',属暖温带-亚热带、湿润-半湿润季风气候;省域面积16.7万km2,矿产资源丰富;全省水资源总量413亿m3,居全国第19位。河南是中国农业大省,小麦、烟草、芝麻产量居中国第1位。2012年河南省人口10 543万人,国民生产总值29 599.31亿元、人均GDP 31 499元。在人口与城镇化的双重压力下,生态环境面临严峻挑战。
1.2 指标体系构建及数据来源
基于区域发展特点、数据有效性与可获得性,本研究以河南省人均GDP(PCG)作为经济增长指标,选取工业废水排放达标率、人均环境污染治理投资额、平均每人生活消费能源等9类指标综合反映该区生态环境水平(EC)的指标(表1),所有数据均来源于《河南统计年鉴》(1994—2013年)。
2 研究方法与模型
2.1 基于BP神经网络的河南省生态环境水平测度
BP(Back Propagation)神经网络是人工神经网络的一种,具有自学习、自组织与自适应性,它由大量基本神经元相互联接构成高度并行的非线性系统,具有大规模并行性处理特征,用以模拟人脑思维[9]。BP神经网络是一种多层次前馈型网络,包括输入层(input)、隐层(hide layer)和输出层(output layer)。主要特点是信号前向传递,误差反向传播[10],能学习和储存大量非线性映射关系,而无需事先了解描述这种映射关系的数学方程,对其后的非样本数据网络也能完成由输入空间向输出空间的正确映射;还能允许输入样本带有误差,通过不断地调整权值改善系统,使网络总误差降到最小,从而避免了人为赋予权重和相关系数的主观影响和不确定性。

表1 河南省生态环境评价指标体系Table 1 The indicator system of ecological environment in Henan province
2.2 序列平稳性检验
散点图法、自相关函数法和单位根检验是几种常用的时间序列平稳性检验方法。本研究采用ADF检验(Augmented Dickey-Fuller Test)(公式1),采用AIC准则做平稳性检验,基于模型极大似然估计对模型阶数和相应参数给出最佳估计[11]。
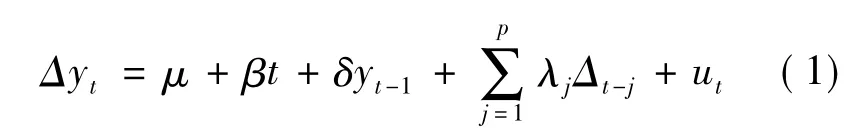
式中:yt为时间序列,ut为白噪声序列,Δ为差分运算符。
2.3 协整性检验
协整关系检验反映2变量不同时间序列间的长期均衡关系,待检验的2个序列必须具有相同的单整阶数。从随机游走序列yt=yt-1+ut可知,其一阶差分序列Δyt=yt-yt-1是平稳序列,称为“一阶单整时间序列”,记为I(1)。以此类推,若一个非平稳序列必须取d阶差分才变为平稳序列,则原序列为d阶单整时间序列,记为I(d)。本研究采用恩格尔-格兰杰法对变量做协整检验,首先求出2变量单整的阶,若2变量单整的阶相同,则用最小二乘法(OLS)估计长期均衡方程yt=bo+b1xt+ut,其中bo和b1表示回归系数的估计值,并保存残差et,作为均衡误差ut的估计值,若et是平稳的,则yt与xt协整、反之不协整。
2.4 格兰杰因果性检验
格兰杰因果性检验假定了有关y和x每一变量的预测信息全部包含在这些变量的时间序列之中。检验要求估计以下方程:

若公式2中x的系数估计值在统计整体的显著不为0,同时公式3中y的系数估计值在统计整体的显著为0,则称x是引起y变化的Grange原因。
2.5 脉冲响应函数
脉冲响应函数能够描述一个内生变量对误差冲击的反应,主要描述当期以及未来远期内生变量受误差冲击的影响力度,由此来判断变量间的动态关系[12]。
向量自回归模型研究序列间的长期动态关系,用于分析系统受到随机扰动项带来的动态冲击影响。

式中:yt为内生变量;xt为外生变量;p为滞后阶数;T为样本数;et为扰动变量。
2.6 方差分解分析
方差分解是分析影响内生变量结构冲击的贡献度,即将系统的均方误差(Mean Square Error)分解成各变量冲击所产生的影响。单个变量对yi的方差贡献率见公式5。

式中:yit表示y的第i个变量,k是变量个数。相对方差贡献度(RVC)描述第j个变量扰动项的冲击方差相对于第i个变量yi的方差贡献度,以此衡量第j个变量对第i个变量的影响程度。
3 生态环境与经济增长关系的动态计量分析实证研究
3.1 河南省生态环境综合水平测度
根据计算工作的特点,网络训练数据通常是由各研究对象的评价标准构成,如人均固定资产投资和人均公共绿地面积等。由于区域可持续发展评价研究尚没有统一的判断标准,本研究使用线性内插法[13],通过构建指标原始数据的最大值和最小值区间,线性设定影响等级。生态环境综合指数为10分,梯度为0.2,由0到10分别表示生态环境综合指数由低到高([0,2]、[2,4]、[4,6]、[6,8]和[8,10]分别表示水平最低、较低、一般、较高和最高)。
将梯度为0.2的51个得分值作为BP神经网络的输出数据,并将评价指标通过线性内插法分为51个等级,最后得到9组共459个训练用的样本数据,作为输入数据。结合前述BP神经网络计算流程,设置隐含层神经元个数为19个,神经网络的拓扑结构为9×19×1。隐含层和输出层网络分别采用Sigmoid型激活函数和Purelin型激活函数,学习速率 Lr设置为0.01,最大循环次数设置为2 000,均方误差MSE为10-4。
经4次训练后网络均方误差达到设定精度(图1-A),采用Scaled共轭梯度算法对BP网络进行仿真验证,考察网络输出结果和期望结果(图1-B)。
将标准化后的河南省生态环境评价指标数据导入训练好的网络,得到1993—2012年河南省生态环境水平综合指数(表2)。除2003年和2007年生态环境水平出现小幅下降外、1993—2012年河南省生态环境水平总体上升。1993—2000年,河南省生态环境水平普遍偏低,原因为此时期居民经济收入较低,政府工作重心放在工业、投资等方面,生态环境保护工作薄弱。2001—2012年,生态环境水平指数由4.646 5增长到9.800 7,这一时期人民收入和生活水平得到持续改善,河南省在发展经济的同时认识到资源开采和环境破坏问题,并开始注重对生态环境的保护。
生态环境整体水平不断上升,其包含的各方面却变化各异。根据标准化后的生态环境各分量指标变化得出生态环境水平分量时序图(图2)。从图2可以看出,人均环境污染治理投资额自2004年起涨幅最为明显,这与近些年经济的快速发展关系密切,经济的快速发展很大程度上拉动了生态环境改善。人均耕地面积整体比较稳定,除2002、2005和2006年达到0.08 hm2·人-1外,其他年份均在0.07 hm2·人-1。森林覆盖率指数波动较多,但整体仍呈现明显上升趋势。生活垃圾无害化处理率在2001—2007年波动下降,2007年后缓慢上升。城市建成区绿化覆盖率除1994、1995年较前一年降低外,其他年份均缓慢上升。人均公共绿地面积、工业固体废弃物综合利用率、工业废水排放达标率均为缓慢上升趋势。生活垃圾无害化处理率先缓慢上升,后几乎保持稳定,偶有波动。平均每人生活消费能源数量显著上升,对生态环境产生负面效应故标准化后的曲线为下降趋势。

图1 BP神经网络训练过程(A)和输出期望相应图(B)Fig.1 Training process of BP NN(A)and the response and expected output of BP NN(B)

表2 河南省生态环境水平综合指数Table 2 The composite score of ecological environment level in Henan Province

图2 生态环境水平各分量时序图Fig.2 Component sequence diagram of ecological environment
3.2 河南省生态环境与经济增长关系的动态计量分析
3.2.1 平稳性和协整检验 利用EViews计量经济学软件,对河南省1993—2012年生态环境(EC)和人均GDP(PCG)2列时间序列进行单位根的稳定性检验(最优滞后期根据AIC准则确定)。时间序列的原始序列、一阶差分和二阶差分ADF检验EViews输出结果见表3。
由表3可知,上述检验统计量值大于5%水平下的DW临界值,EC序列存在单位根,是非平稳序列。对序列EC进行一阶差分并进行ADF检验,依然得出AI的检验统计量大于5%水平下的DW临界值,为非平稳序列。需对AI进行二次差分,得出AI的检验统计量小于5%水平下的DW临界值,序列EC为平稳序列,且EC具有二阶单整性,即EC~I(2)。同理,可得出PCG为二阶单整序列,PCG ~I(2)。
因EC和PCG属同阶单整,采用恩格尔-格兰杰两步法检验判断它们之间是否存在协整关系。对EC和PCG进行OLS回归,得到方程PCG=8.175 449+0.658 7 ×EC,t=(46.267)(6.039)。
对OLS回归方程残差时间序列做单位根平稳性检验,检验统计量的值均小于在5%显著性水平下的DW临界值。说明模型不存在谬误回归,二者存在协整关系;随着EC每提高1个单位,会引起PCG提高0.658 7个单位。
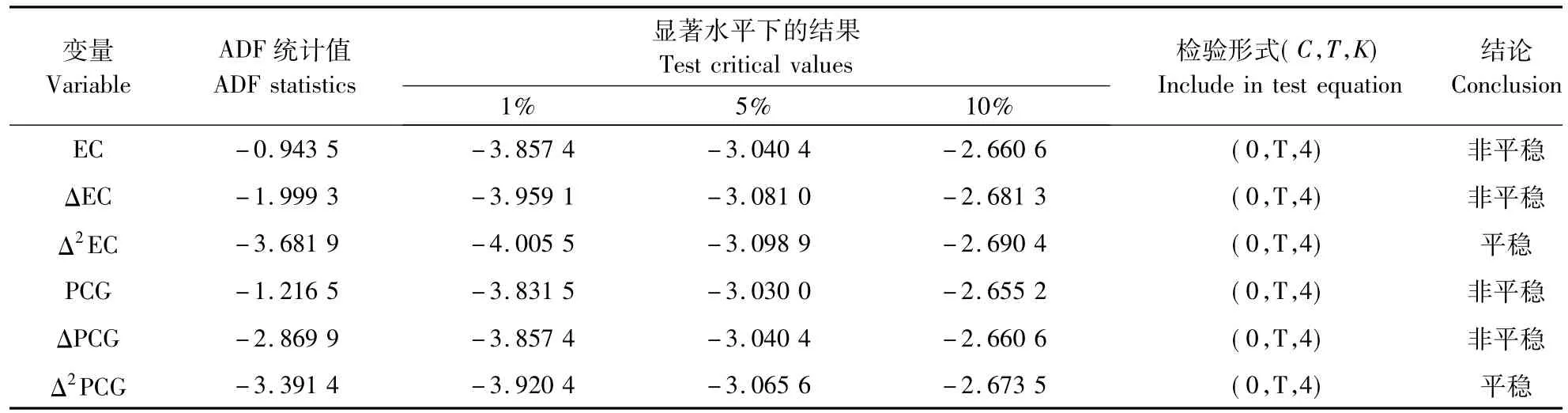
表3 序列平稳性检验结果Table 3 Result of serial stability test
3.2.2 Granger因果关系检验 对EC和PCG进行Granger因果关系检验,结果显示:当滞后期为2时,在5%的概率下接受了“EC不是PCG的格兰杰原因”的原假设,而拒绝了“PCG不是EC的格兰杰原因”的原假设;滞后期为3时,在5%的概率下接受了“EC不是PCG的格兰杰原因”的原假设;滞后期为4时,5%的概率下拒绝了“EC不是PCG的格兰杰原因”的原假设。以上结果表明,经济增长在第2滞后期就是环境变化的Granger原因,经济增长对环境水平有着直接的影响;在滞后期为2、3时生态环境水平均不是经济发展的Granger原因,直到第4期才是经济发展的原因,表明环境对经济有影响但存在滞后性,主要由于生态环境改善所能带来的社会经济效益需要一定的时间才能转换为企业的外部效益。
3.2.3 脉冲响应函数和方差分解 在验证EC和PCG存在Granger因果关系的基础上,运用Eviews建立EC和PCG的自回归模型,最优滞后阶数根据AIC和SC最小标准准则确定。

基于自回归模型建立它们之间的脉冲响应模型,作用时间为10年。检验结果见图3。生态环境水平对经济增长新息的一个标准差扰动在第1期为0,第2期达到负向最大值-0.2,第3、4期逐渐趋于0,在第4期之后呈现稍稳定伴有波动的正向响应(图3-A)。说明随着社会经济水平的提高,生态环境水平将不断提高,经济增长使公众对于上层建筑和生活环境改善的需求不断提高,同时有能力将更多的财力物力投入到生态环境的保护和改善中,并依靠科技进步不断开发新能源、减少环境污染、保护自然资源;而初期经济增长对生态环境水平产生负向效应,主要由于社会发展水平较低时,科技达不到相应水平,要发展经济就需要牺牲相应的资源环境条件。
经济增长对生态环境水平新息的一个标准差扰动在第1、2期达到负向最大值-0.04~0,第3期基本为0而后缓慢上升,总体维持稳定的正向响应、波动较小(图3-B)。说明随生态环境水平的提高,经济增长呈现先负向后正向的变化;因生态环境的保护和改善需要投入大量财力和人力,而环境优化需要一定时间的积累才能产生经济效益。
图4对EC和PCG的预测均方误差进行分解,第1期生态环境波动仅受自身变化影响,第2期降低至85.04%后出现小幅缓慢下降,第10期达到76.39%;经济增长对生态环境变化的冲击在第2期开始显现并逐步增长,第10期增至23.61%(图4-A)。
第1期经济增长受自身波动的影响为85.17%、第4期逐渐上升至94.33%;后缓慢下降至第9、10期开始稳定。第1期生态环境对经济增长的冲击最大为15.86%,后缓慢下降至第四期达到最小值 5.67%,后又逐渐上升至最大值15.86%,并有逐渐增长的趋势。总体上生态环境水平与经济增长均是自身预测误差方差的主要来源,但长期来说,二者对彼此预测误差方差的贡献都将越来越大,当社会发展达到一定水平后,二者将同步上升。

图4 生态环境水平预测及经济增长预测方差分解图Fig.4 The results of variance decomposition
4 结论
本研究应用BP神经网络分析研究了1993—2012年河南省生态环境与经济增长的关系。结果表明:(1)1993年后河南生态环境水平总体呈上升趋势,生态环境综合指数与经济增长长期均衡,生态环境综合指数每提高1个单位,引起人均GDP增长0.658 7个单位。(2)河南生态环境水平与经济增长互为Granger原因,短期内生态环境水平对经济增长的冲击响应为负向,第4期后变为相对稳定伴有小幅波动的正向响应。(3)生态环境水平与经济增长均是自身预测误差方差的主要来源,在达到一定程度后,二者方表现为同步增长;经济增长有助于生态环境的改善并最终促进经济可持续发展。
应当注意到,伴随生态环境整体水平上升,人均公共绿地面积、工业固体废弃物综合利用率、工业废水排放达标率、生活垃圾无害化处理率、人均环境污染治理投资额都呈总体上升趋势,但人均耕地面积稍有下降,平均每人生活消费能源数量显著上升。因此,河南省应在发展经济的基础上,继续实施在城市城绿化方面的有效措施、进一步优化对废水、固体废弃物及垃圾的处理的基础上,更加注重耕地面积减少和耕地质量下降等问题,切实保护耕地,提高资源利用效率、加快新能源的开发利用、大力发展低耗能高产出的集约化产业。同时大力发展多功能生态农业,优化产业结构、加大科技和经济投入,实现经济与环境的可持续发展。
[1] GROSSMAN G,KRUEGER A.Economic growth and the environment[J].Journal of Economics,1995,110:353-377.
[2] PANAYTOU,T.Environment for growth in central America:environmental management for sustainability and competitiveness[M].Cambridge,MA:Harvard Press,2001.
[3] BRAIN R COPELAND,M SCOTT TAYLOR.Trade,growth,and the Environment[J].Journal of Economic Literature,2004,42(1):7-71.
[4] 吴开亚,陈晓剑.安徽省经济增长与环境污染水平关系研究[J].重庆环境科学,2003,25(6):9-12.
[5] 沈满洪,许云华.一种新型的环境库兹涅茨曲线——浙江省工业化进程中经济增长与环境变迁的关系研究[J].浙江社会科学,2004,20(4):53-57.
[6] 邢秀凤,刘颖宇.山东省经济发展与环境保护关系的计量分析[J].中国人口·资源与环境,2006,16(1):58-61.
[7] 王长建,张小雷,杜宏茹,等.近30a新疆城市化与生态环境互动关系的动态计量分析[J].中国沙漠,2012,32(6):1794-1802.
[8] 周玄德,孜比布拉·司马义,严 姗,等,克拉玛依市经济增长与生态环境关系的计量分析[J].水土保持通报,2013,33(2):236-240.
[9] 韩力群.人工神经网络理论、设计及应用[M].北京:化学工业出版社,2007:14-54.
[10] 杜 东,庞庆华,吴 炎.现代综合评价方法与案例精选[M].北京:清华大学出版社,2008:87-97.
[11] ENGLE R F,GRANGER C W J.Cointegration and error correction:representation,estimation and testing[J].Econometrica,1987,55(2):251-276.
[12] 朱红根,卞琦娟,王玉霞.中国出口贸易与环境污染互动关系研究——基于广义脉冲响应函数的实证分析[J].国际贸易问题,2008(5):80-86.
[13] 刘 哲.Bernstein-Bézier系数及径向基函数神经网络的插值与收敛性研究[D].银川:宁夏大学,2013.

