火电厂SCR烟气脱硝系统建模与喷氨量最优控制

周 鑫， 吴 佳

（浙江浙能台州第二发电有限责任公司，浙江 台州 317109）

火电厂SCR烟气脱硝系统建模与喷氨量最优控制

周 鑫， 吴 佳

（浙江浙能台州第二发电有限责任公司，浙江 台州 317109）

SCR（选择性催化还原）是发电厂目前普遍采用的烟气脱硝方法，脱硝系统的喷氨量不仅影响烟气脱硝的效率，过量喷氨也会造成氨逃逸率升高，导致环境的二次污染。SCR系统反应机理复杂，具有非线性、大惯性等特点，传统PID控制方法无法实现喷氨量的精确控制。将KPLS（核偏最小二乘方法）与GA（遗传算法）结合，提出了GA-KPLS建模方法，并建立了SCR系统模型。仿真结果表明，模型具有较好的学习及泛化能力。将SCR模型应用于模型预测控制方法中，实时计算最优喷氨量，实现了对喷氨量的精确控制。实验结果表明，此方法与传统PID控制方法相比，显著提高了脱硝率，同时降低了氨逃逸率。

选择性催化还原；烟气脱硝；核偏最小二乘；遗传算法；最优控制

0 引言

发电厂锅炉燃烧产生的NOX排放到大气中会对环境造成严重污染[1]。降低NOX排放的措施分为2种：一是燃烧中减排，即采用分级燃烧或改进燃烧器等方法使燃煤产生的NOX量减少；二是燃烧后减排，即通过加装脱硝装置对尾部烟气进行脱硝处理。SCR（选择性催化还原方法）烟气脱硝系统反应机理复杂，脱硝效率受到喷氨量、反应温度、烟气速度、催化剂活性等因素影响，其中喷氨量对脱硝效果影响最大，是关键的可调因素。喷氨量过少会导致烟气NOX含量超标；喷氨量过多，不仅会提高氨逃逸率造成二次污染，同时也会增加脱硝成本。

随着预测控制、核偏最小二乘、神经网络以及支持向量机等技术的发展和在工业上的成功应用，可以充分利用发电厂历史运行数据建立SCR烟气脱硝系统模型，同时采用先进控制算法，实现喷氨量的最优控制，在降低NOX排放的同时减少脱硝成本。采用KPLS（核偏最小二乘）方法建立SCR烟气脱硝系统模型，利用遗传算法优化核函数参数，从而提高模型的学习和泛化能力，将SCR模型与预测控制方法相结合，设计出基于GA-KPLS的喷氨量最优控制系统。利用发电厂实际运行数据进行仿真验证，实验结果表明GAKPLS喷氨量最优控制系统在显著降低NOX排放量的同时减少了氨逃逸率。

1 SCR喷氨烟气脱硝系统装置

某1 000 MW超超临界机组SCR烟气脱硝系统结构如图1所示。

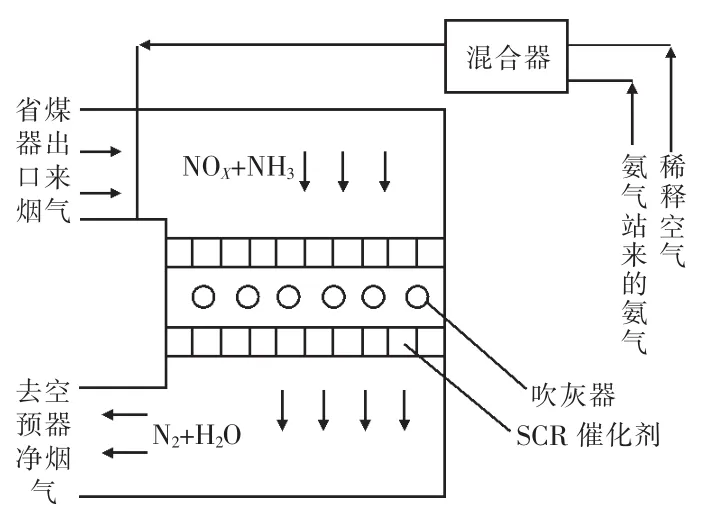
图1 SCR烟气脱硝系统示意

该SCR喷氨烟气脱硝系统采用TiO2作为催化剂。稀释空气与来自氨气站的氨气混合，经喷氨控制阀调整喷氨流量后通过喷嘴喷出，并与烟气充分混合。混合气体在TiO2的催化作用下发生选择性催化还原反应，烟气中的NOX与NH3发生反应，生成无害的氮气和水，从而达到烟气脱硝的目的[2]。SCR脱硝系统主要反应过程如下：

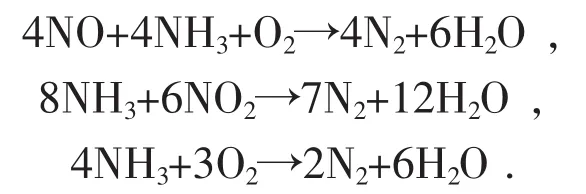
实际运行中同时会发生一些副反应并产生一些有害副产物：

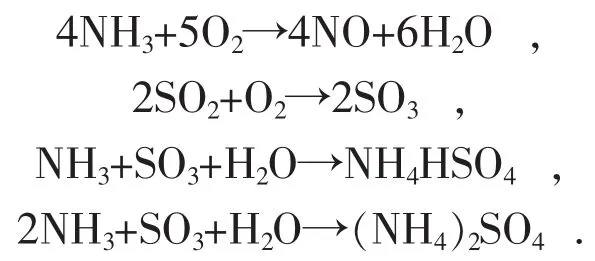
过量喷氨不仅会增加SCR系统中氨气浓度，提高副反应速度，导致重新生成NOX，影响脱硝效率，同时，过量的NH3与SO3反应生成硫酸氢氨等有害副产物，这些副产物会导致催化剂失活或者堵塞催化剂孔板，从而降低脱硝效率，还会腐蚀管道影响机组的安全运行，同时，氨逃逸也会造成二次污染[2]。

机组运行工况的不断变化会导致烟气中NOX浓度产生剧烈波动，传统PID（比例-积分-微分）控制效果并不理想。因此，必须设计更优的自动控制系统控制喷氨量，以最合理的喷氨量保证脱硝效率，同时减少不利副产物的生成，避免二次污染。

2 SCR烟气脱硝系统模型

2.1 GA-KPLS模型

KPLS是将核函数技术与偏最小二乘算法结合，利用非线性函数提高输入变量的维度，把输入空间映射到高维特征空间并应用偏最小二乘求解，从而构建出一种解决非线性问题的算法。核函数是核偏最小二乘算法中的关键因素，但如何选择、确定核函数目前尚无理论参考。通常认为径向基函数一般情况下优于其他常用的核函数，因此选用径向基函数作为核函数。

径向基核函数中包含一个参数σ，它的确定尚无统一方法，采用GA（遗传算法）对其进行寻优。遗传算法按照适者生存和优胜劣汰的原理，经过迭代计算求取最优近似解，具有良好的全局搜索能力且计算速度快。

设变量X∈Rn×p，Y∈Rn，p为自变量个数，n为观测样本个数，对数据进行归一化处理。KPLS算法描述如下：

（1）计算核矩阵K。核矩阵元素计算公式为：

（2）随机初始化Y的得分向量u。

（3）计算X的得分向量t并归一化。

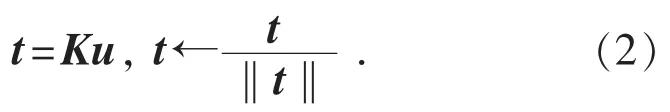
（4）计算权值向量c。

（5）计算Y的得分向量u并进行归一化。

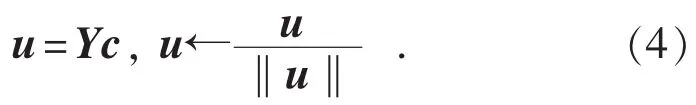
（6）重复步骤（2）—（5）直至t收敛。

（7）缩小K与Y，重复步骤（2）—（5）直至提取p个t与u。

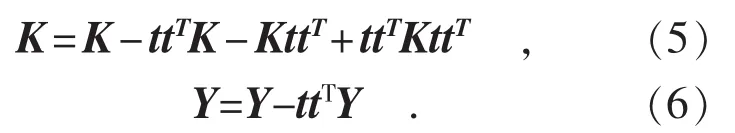
训练样本拟合公式为：

式中：T与U为得分向量t与u构成的矩阵。

预测样本拟合公式为：

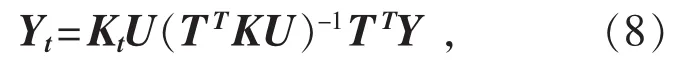
式中：Kt为预测核矩阵；Yt为模型预测结果。

2.2 仿真试验与结果分析

根据工程实际和理论分析，选取SCR入口NOX浓度、喷氨量、烟气温度和机组负荷4个影响脱硝效率的因素作为SCR烟气脱硝系统模型的输入量，SCR出口NOX浓度作为输出量。从运行历史数据中选取150组作为样本，其中100组作为训练样本，50组作为预测样本。采用遗传算法对参数σ进行寻优，寻优结果为σ=0.01。模型训练及预测效果如图2与3所示。

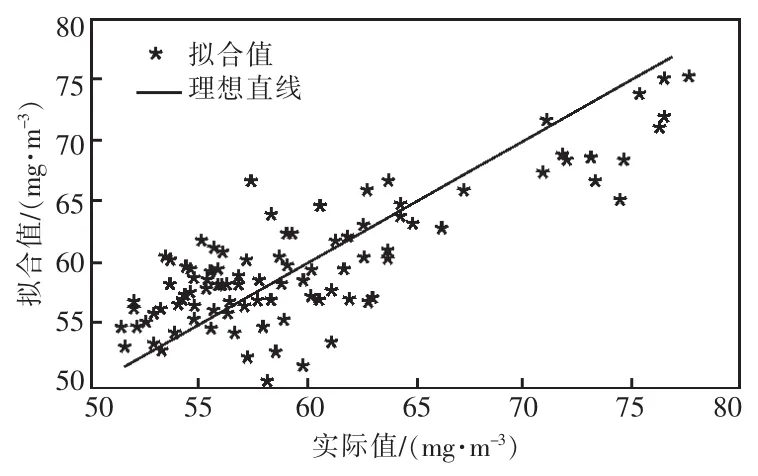
图2 KPLS模型训练效果

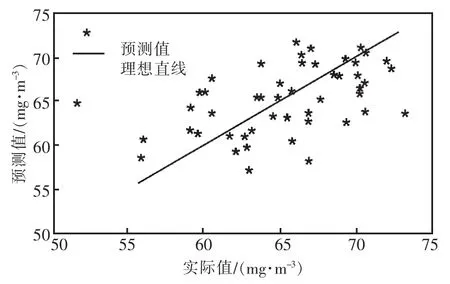
图3 KPLS模型预测效果

模型精度评价指标采用RMSE（均方根误差）和MAPE（平均绝对百分比误差），计算公式如下：

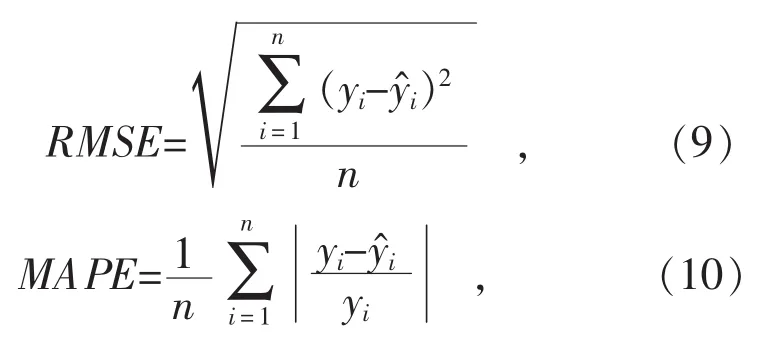
式中：yi为测量值为预测值；n为预测样本的个数。

SCR系统KPLS模型的训练及预测精度分别为RMSET=3.958 4 mg/m3，RMSEP=4.499 5 mg/m3，MAPET=5.41%，MAPEP=5.71%，其中下标T和下标P分别代表训练和预测评价指标。从图2与3中可以看出，拟合值和预测值分布在理想直线附近，说明拟合及预测效果较好，模型具有较强的学习能力和泛化能力。

3 喷氨量最优控制的仿真

3.1 模型预测控制

模型预测控制是一种智能控制算法，根据模型预测的输出相应调整输入量，通过极小化目标函数求解输入量的变化量，从而使实际输出与设定值保持一致。模型预测控制算法被转化为求解非线性优化问题：

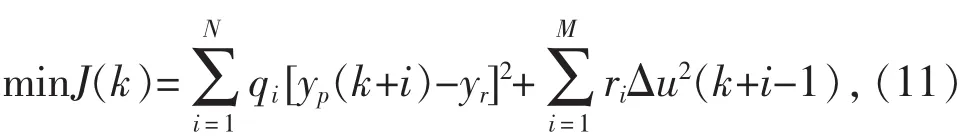
式中：yp为模型输出；yr为设定值；Δu为输入量的变化量；N与M分别为预测长度和控制长度；q与r分别为输入输出的权重系数。

针对上面的非线性优化问题，采用PSO（粒子群优化）算法求取最优解。PSO算法具有简单、容易实现、调整参数少的优点。混沌是非线性系统中普遍存在的现象。混沌运动具有内在随机性、非规则有序性和遍历性等特点。采用Logistic映射xn+1=4xn（1-xn）产生混沌变量，其中n为迭代次数；初始值x0∈（0，1）且x0≠0.25，0.5，0.75。采用这种方法生成PSO算法的初始种群，可以使种群内粒子分布较为均匀，具有多样性、遍历性的特点，有利于全局搜索。

基于以上建模方法以及预测控制算法，提出一种SCR喷氨量最优控制方法。首先应用GAKPLS方法建立SCR系统模型，再利用模型以及粒子群算法对喷氨量进行优化，通过改变喷氨量来提高脱硝效率，达到最优控制目的。控制算法流程如图4所示。

3.2 实验结果和分析

以某1 000 MW超超临界锅炉SCR烟气脱硝系统作为研究对象，选取150组运行历史数据作为训练及预测样本，其中训练样本个数为100，预测样本个数为50。对训练及预测样本进行预处理，利用遗传算法对核函数参数进行寻优，建立SCR烟气脱硝系统的KPLS模型。喷氨量最优控制采用粒子群算法求解非线性优化问题。其中，设定惯性因子 ω=0.729，学习因子 c1=c2=1.494 45，种群大小为15，迭代次数为50，喷氨量改变量的范围设为0～100 kg/h，根据国家相关规定SCR出口NOX浓度设定值设为50 mg/m3。仿真实验结果如图5与6所示。

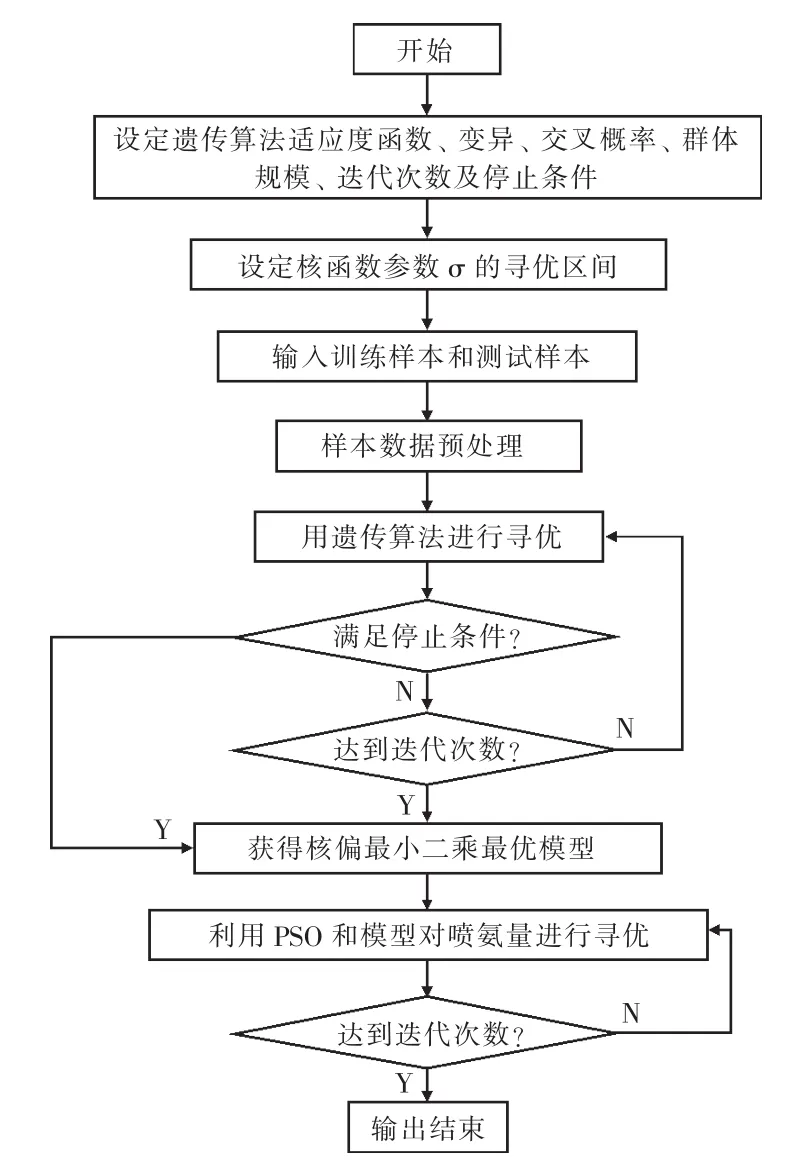
图4 喷氨量最优控制算法流程

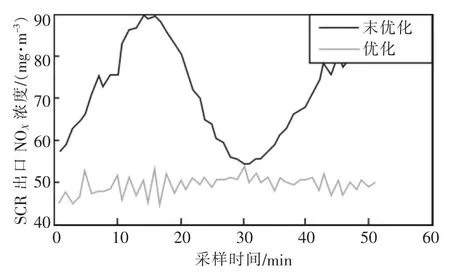
图5 SCR出口NOX浓度

SCR脱硝系统反应机理复杂，具有大惯性、非线性等特征，传统PID方法无法取得良好的控制效果。从图5—6可知，采用传统PID控制时平均脱硝率只有61.45%，SCR出口NOX平均浓度为71.630 6 mg/m3。相比之下，模型预测控制不需要深入了解被控对象的内部机理，有效提高了系统的鲁棒性。同时，模型预测控制对喷氨量进行滚动寻优，具有较好的动态控制效果。对喷氨量进行最优控制后，平均脱硝率为73.13%，SCR出口NOX平均浓度为49.578 5 mg/m3，脱硝效果有了显著提升。

由于模型预测控制的性能指标中引入了喷氨量的变化量，使得SCR出口NOX浓度在跟踪设定值的同时尽量减少喷氨量的变化，实现喷氨量的精确控制，避免阀门频繁调整带来的损耗及安全隐患。仿真实验结果如图7与8所示。

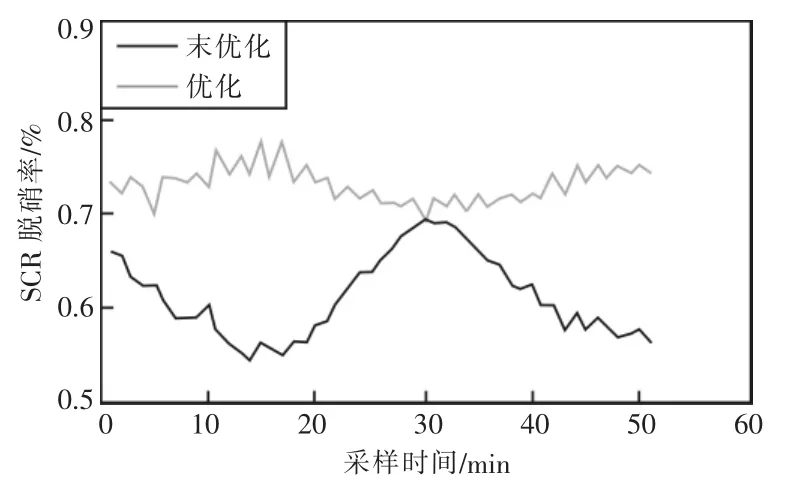
图6 SCR脱硝率

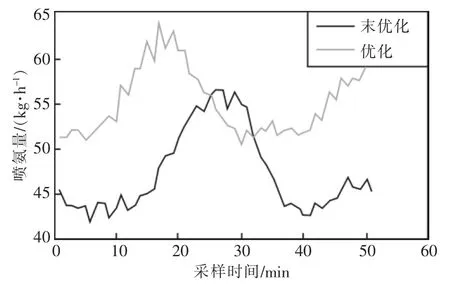
图7 喷氨量

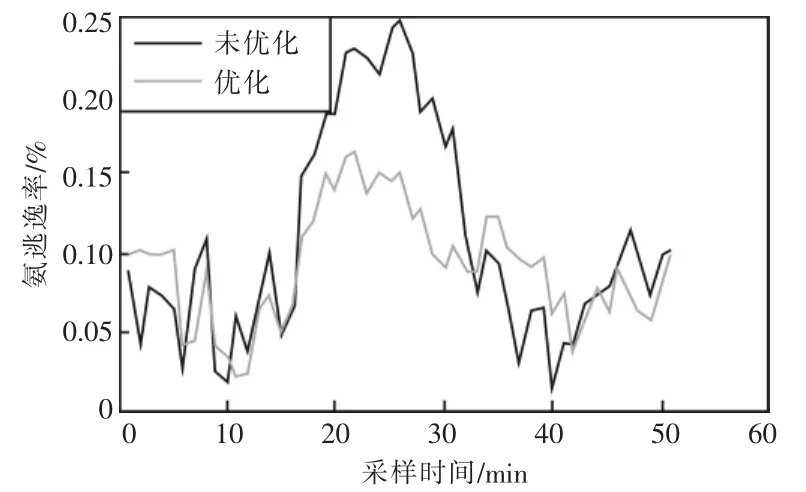
图8 氨逃逸率

传统PID控制方式仅利用SCR出口NOX浓度进行反馈控制，很难解决工况波动情况下SCR系统的非线性和大惯性问题，结果造成过量喷氨，导致氨气逃逸，对环境造成了二次污染。采用传统PID控制时，平均喷氨量为47.266 4 kg/h，平均氨逃逸率为10.79%。采用最优控制后，喷氨量得到了精确控制，平均喷氨量为55.598 0 kg/h，平均氨逃逸率为9.89%。平均氨逃逸率有所下降，说明过量喷氨的情况得到了改善。同时，平均喷氨量有所上升，因为脱硝率有了显著提高，脱硝反应所需的氨气量也随之上升，导致了喷氨量的增加。

4 结语

利用GA-KPLS方法建立了SCR烟气脱硝系统模型，模型具有较好的学习及泛化能力，充分反映了SCR系统的非线性过程。将模型与预测控制方法相结合，利用PSO算法对喷氨量进行最优控制。仿真实验结果表明，模型预测控制在显著提高脱硝率的同时减小了氨逃逸率，避免了过量喷氨，实现了喷氨量的最优控制。模型预测喷氨量最优控制具有一定的工程应用价值，为喷氨量的精确控制提供了一种有效方法。

[1]王春林，周昊，李国能，等.基于遗传算法和支持向量机的低NOX燃烧优化[J].中国电机工程学报，2007（11）∶40-44.

[2]周洪煜.超临界锅炉烟气脱硝喷氨量混结构-径向基函数神经网络最优控制[J].中国电机工程学报，2011（5）∶108-113.

[3]阎纲.基于最小二乘支持向量机的铝电解过程建模与控制研究[D].长沙：中南大学，2012.

[4]杜振，钱徐悦，何胜，等.燃煤电厂烟气SCR脱硝成本分析与优化[J].中国电力，2013，46（10）∶124-128.

[5]梁川，沈越.1000MW机组SCR烟气脱硝系统优化运行[J].中国电力，2012，45（1）∶41-44.

[6]董建勋，王松岭，李永华，等.选择性催化还原烟气脱硝过程数学模拟研究[J].热能动力工程，2007，22（5）∶569-573.

[7]周响球,杨晨.选择性催化还原脱硝反应器数学模型及仿真[J].重庆大学学报：自然科学版，2007，30（6）∶39-43.

[8]曹志勇，谭城军，李建中，等.燃煤锅炉SCR烟气脱硝系统喷氨优化调整试验[J].中国电力，2011，44（11）∶55-58.

[9]NOVA I，LIETTI L，TRONCONI E，et al.Transient response method applied to the kinetic analysis of the De-NOX-SCR reaction[J].Chemical Engineering Science，2001，56（4）∶1229-1237.

[10]赵乾.SCR烟气脱硝系统模拟优化及喷氨量最优控制[D].重庆：重庆大学，2012.

[11]LIETTI L，NOVA I，CAMURRI S，et al.Dynamics of the SCR-DeNOXreaction by the transient-response method[J]. Aiche Journal，1997，43（10）∶2559-2570.

[12]周荔丹.广义预测控制算法及应用研究[D].长沙：湖南大学，2002.

[13]黄山，蒋鹭，王天才，等.神经网络与遗传算法结合的球团竖炉燃烧优化[J].东南大学学报：自然科学版，2012，42（1）∶88-93.

[14]董建勋.燃煤电厂SCR烟气脱硝试验研究及数学模型建立[D].保定：华北电力大学，2007.

[15]穆朝絮，张瑞民，孙长银.基于粒子群优化的非线性系统最小二乘支持向量机预测控制方法[J].控制理论与应用，2010，27（2）∶164-168.

（本文编辑：陆 莹）

Modeling of SCR Flue Gas Denitration System and Optimal Control of Spraying Ammonia Flow in Thermal Power Plant

ZHOU Xin，WU Jia
（Zhejiang Zheneng Taizhou Second Electric Power Generation Co.，Ltd.，Taizhou Zhejiang 317109，China）

Selective catalytic reduction（SCR）method is usually used for flue gas denitration in thermal power plant.Spraying ammonia flow of denitration system can affect the efficiency of flue gas denitration And excess ammonia spraying results in higher rates of ammonia escape which cause secondary pollution of the environment.Reaction mechanism of SCR system is very complex and it has the characteristics of nonlinearity and large inertia.Therefore，it is difficult for the traditional PID control methods to achieve precise control of the amount of ammonia injection.Combining the kernel partial least squares（KPLS）and genetic algorithm（GA），GA-KPLS modeling method is proposed and the SCR system model is established.The simulation results show that the learning and generalization abilities of the model are both better.In order to precisely control the amount of ammonia spraying，model predictive control method is used to calculate the real-time optimal amount of ammonia spraying.Experimental results show that compared with traditional PID control this method significantly improves the denitration rate as well as reduces the ammonia escape rate.

selective catalytic reduction；flue gas denitration；kernel partial least squares；genetic algorithm；optimal control

X701.3

B

1007-1881（2015）11-0015-05

2015-09-17

周 鑫（1990），男，助理工程师，从事发电厂机组运行工作。