拉曼光频移对原子干涉测量中原子数的影响
李超辰,王宇,武腾飞,茹宁,季俊云
(中航工业北京长城计量测试技术研究所,北京100095)
0 引言
随着激光冷却技术的不断发展,冷原子干涉技术在重力加速度精密测量等领域获得成功应用[1],展示出了极大的发展潜力。在冷原子干涉测量过程中,影响测量结果精度的因素众多,激光相对原子运动的多普勒频移是其中一项。在原子受重力自由下落过程中,由于速度以重力加速度变化,因此感受的激光频率也相应发生变化。普遍情况下,原子的自由下落过程中会受到三次脉冲激光照射,各个冷原子干涉测量研究小组都会对这三次激光脉冲的频率进行精确的多普勒频移补偿。但是,由于作用于原子的脉冲激光持续时间极短(μs 量级),在这段极短时间内,原子依然产生速度变化,如果用固定频率激光脉冲照射,即使进行了多普勒频移补偿,原子真实感受到的激光频率仍会因多普勒频移效应而存在啁啾。对这一光频率变化的处理,各个研究团队的做法并不一致[1-6]。在原子整个下落过程中,用扫频方式补偿多普勒频移是普遍的做法,但扫频的具体参数,决定了光脉冲时间内,频移是否以及如何被补偿,当扫频间隔超过拉曼脉冲持续时间(10 μs 量级)时,脉冲持续时间内的多普勒频移无法被补偿,这一点在绝大部分文献中都没有被明确分析过。例如,S.Chu 曾在文章[7]中提到过脉冲持续时间内的多普勒效应问题,但主要为定性描述,没有具体的过程介绍或结果影响分析。国内中科院数物所曾研究过专门用于冷原子干涉的声光调制器信号驱动,提及其扫描步进时间为6.6 ns,信号调节响应时间107 μs,但公开发表的文章中并未给出微秒量级的微波扫频信号信息,以及关于扫频脉冲过程中的多普勒补偿问题。
本文就拉曼激光脉冲持续时间内,原子相对运动产生的多普勒频移展开研究,通过分析频移对原子团跃迁概率的影响,计算有效原子的损失,推算其对干涉测量条纹对比度产生的影响。
1 基本原理
1.1 冷原子干涉测量原理
干涉是波动性的结果,常见的光波、机械波都存在干涉。由量子力学预言,实物粒子也具有波动性,即人们熟知的德布罗意物质波,因此,实物粒子也同样可以发生干涉现象,并被用于干涉测量。
原子物质波的干涉分外态与内态干涉,这里讨论内态干涉,即利用原子能级跃迁产生的干涉[6]。将原子模型简化为忽略自发辐射的二能级系统,原子内态干涉操作采用普遍的拉曼脉冲型干涉方式,如图1所示。
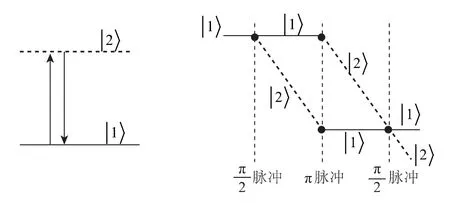
图1 原子干涉的能级跃迁过程
原子波函数初始处于1 态,经过一束拉曼π/2 脉冲作用,原子波函数分裂,原子拥有50%的概率处于1 态,50%的概率处于2 态。经过一段时间T 的自由飞行后,原子再次与一束拉曼π 脉冲作用,处于1态的波函数附加拉曼光相位信息后跃迁到2 态,处于2 态的波函数同样附加拉曼光相位信息后跃迁回到1态,由于两部分波函数所处空间位置不同,其携带的拉曼光相位信息也因而不同。再经过一段时间T 的自由飞行后,原子与第三束拉曼π/2 脉冲作用,两部分波函数分别产生分裂,得到4 部分波函数。其中,同处于同一能态的两个波函数相干叠加,叠加干涉的结果体现在原子在不同态上的存在概率。因此,通过探测原子处于1,2 态概率即可获得不同路径原子波函数携带的拉曼激光相位信息,进而得到重力加速度量值。
1.2 原子与拉曼激光的作用[7]
考虑常用的87Rb 原子,其三能级跃迁如图2所示,其中基态(S1/2)具有两个超精细能级(F=1 及F=2),激发态为P3/2。
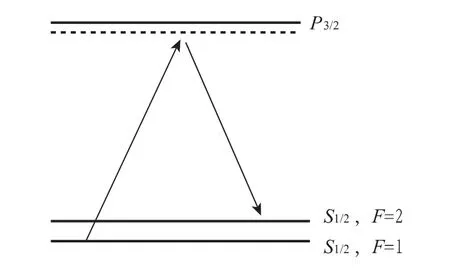
图2 87Rb 拉曼跃迁能级
在实际过程中,原子向P3/2的跃迁存在一个失谐Δ,以抑制自发辐射。将该三能级系统简化为二能级系统,原子状态由波函数| ψ〉定量描述,则该系统内的任意原子波函数可表示为
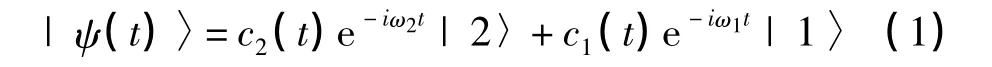
式中:c1,c2模的平方代表原子处于1 态、2 态的概率,| 1〉,| 2〉为原子处于1,2 能级的本征波函数,ω1,ω2为能级本征角频率。考虑到对于二能级系统,拉曼激光将等效为微波,其微波角频率ω 为两激光的角频率ω1r与ω2r之差,有
当原子受到拉曼光照射时,系统哈密顿量中应存在定态项H0和相互作用项Hi,用来定量表示激光对原子的作用,于是哈密顿量整体成为
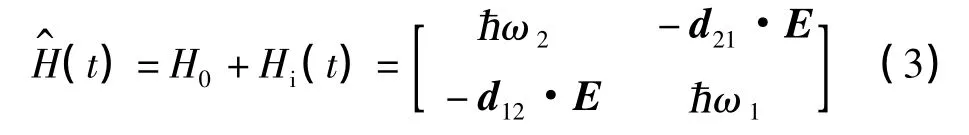
式中:d21与d12分别为1,2 能级间跃迁电偶极矩;ħ为普朗克常数;E 为激光的光电场,是位置矢量r 和时间t 的函数。有

式中:E0为光电场振幅;φ0为初相位。一般的,若d=d21=d12,分别定义拉比频率Ω 及其复数共轭Ω*、共振角频率和激光失谐δ,有

一并代入薛定谔方程,并利用旋波近似得到最终的微分方程为
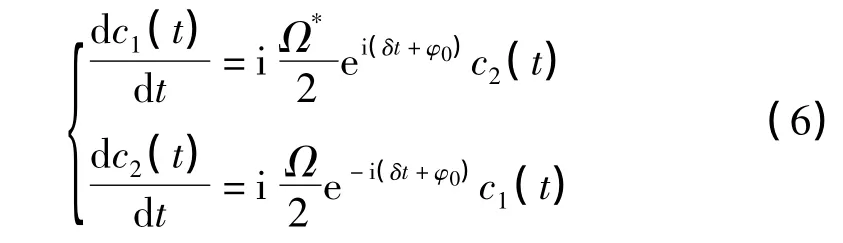
上述二元微分方程组可化为一元二次齐次微分方程,求解得到通解并代入两态初始条件c1(0)=1,c2(0)=0得到
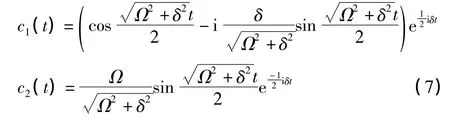
则1 态、2 态的分布概率分别为

公式(8)表示拉曼光与原子作用时,原子在1,2能级的分布概率p1,p2的定量关系。易知,随着拉曼光的持续照射,原子将在1,2 能级间不停地振荡。
2 拉曼光多普勒频率啁啾
在实际情况中,因为光子本身具有动量,当原子(核外电子)吸收光子由低能级跃迁至高能级;或放出光子,由高能级跃迁至低能级,必然伴随自身速度的变化。另外,一团原子气体即使经过激光冷却,温度达到μK 量级,也具有约100 mm/s 的平均速度,这些都会使原子感受到的激光频率受到多普勒效应的影响。
因此,当考虑到原子速度的改变时,将动量作为一个新指标引入波函数,相应的二能级系统本征波函数表示为| 1,p-ħk1r〉,| 2,p +ħk2r〉,表示在动量p 附加了一个光子反冲动量。经过类似推导,得到原子能级跃迁概率[8]为

其中,
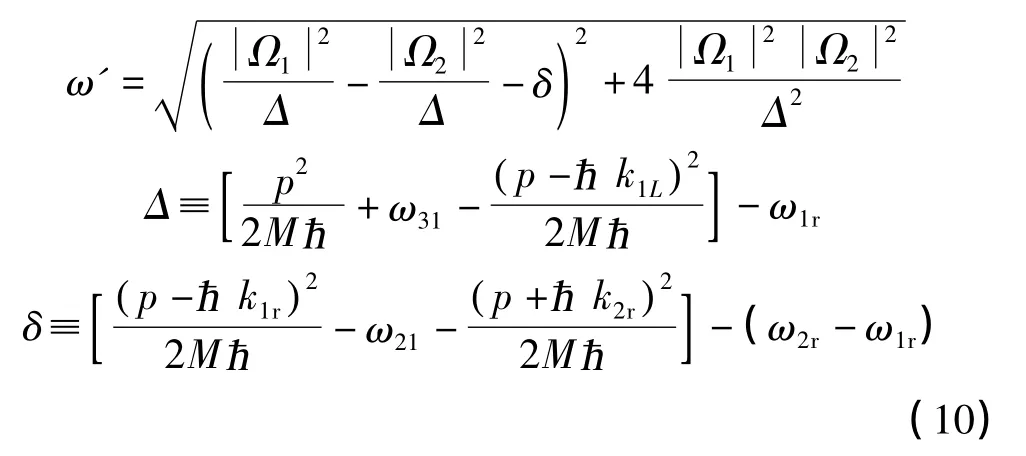
式中:M 为Rb 原子质量;Δ 为中间能级的失谐;ωij表示i,j 能级间本征频率差;Ω1,Ω2为从两个超精细基态跃迁至中间态的拉比频率。式(9)的物理含义是,当原子初始处于[c1(t0),c2(t0)]状态时,若存在一组角频率为ω、光电场振幅为E 的拉曼激光稳定作用于原子,则原子将以式(9)所述的规律在1,2 两能级间跃迁。
现在考虑冷原子团在干涉测量过程中与激光相互作用存在的多普勒频移情况。首先,假设拉曼脉冲作用时间极短,忽略脉冲持续过程中原子的速度变化,在三次拉曼激光照射冷原子团的时刻,原子因为自由落体运动(不考虑上抛,初始时刻速度为0 m/s),速度一直在增加。不妨设脉冲间隔时间T=1s,当地重力加速度g=9.801 m/s2,则原子在三个时刻的速度分别为0,9.801,19.602 m/s。原子感受到的由两束对射激光组成的拉曼光频率为
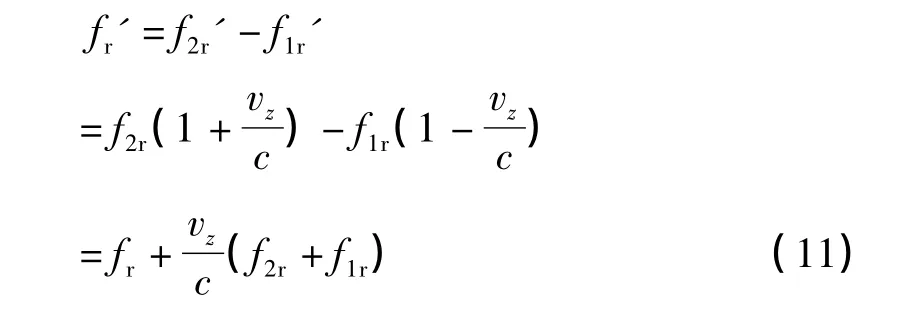
式中:vz为原子纵向速度(沿z 轴);f2r',f1r'为拉曼光两频率各自的多普勒频移;fr为无多普勒频移时的基础频率,f1r,f2r为拉曼激光频率。以图2 中的87Rb 跃迁为例,对应原子三个时刻速度的拉曼光多普勒频移fr'分别为0 Hz,25.1 MHz 和50.2 MHz。实验上,可以通过声光晶体等光学移频方法,对上述多普勒频移进行补偿。
激光的精确移频需要微波频率源产生标准信号,这个信号的质量越高,对整个测量系统引入的误差就越小。因为激光直接与原子相互作用,因此,光学噪声应予以尽量降低。在拉曼激光脉冲的数十微秒量级的持续时间内,精确调节标准微波信号并压制噪声,需要额外的电学设计。如果使用固定频率标准微波信号,即固定拉曼激光频率,本节后半部分将计算脉冲持续时间内,多普勒频移效应对原子跃迁影响的大小。
由于式(9)给出的是固定频率拉曼激光作用下原子的跃迁规律,而原子感受到的是频率存在啁啾变化的拉曼光,因此文本采用类似微分的方式对其进行数值迭代计算。
设任意时刻t0,原子处于[c1(t0),c2(t0)]态,经角频率差为ω 的拉曼光作用dt 时间,原子处于[c1(t0+dt,ω),c2(t0+dt,ω)]态。若dt 趋于零,则ω 趋于ω0,可以利用ω0替代ω,原子态表示为[c1(t0+dt,ω0),c2(t0+ dt,ω0)]。利用上述方法,采用Matlab数值迭代计算拉曼光频率啁啾下的原子跃迁概率变化规律,过程如图3所示,只要选择dt 的大小,控制数值偏差在允许范围即可。

图3 拉曼光频率啁啾下的原子跃迁过程
代入实际参数进行计算,设拉曼光光强Ⅰ=1 mW,光斑半径R=10 mm,脉冲持续时间T=1.5×10-4s(约1.5 倍拉比周期),迭代时间间隔dt=T/1000,拉曼光频率f=384.23×1012Hz。
分别在补偿多普勒频移拉曼光和定频率拉曼光作用下的不同速度原子跃迁概率如图4所示。其中图4(a)和(b)为原子态随时间的变化,横轴表示时间演化,灰度表示原子态的分布,初始时刻t=0,原子全部处于1 态,在拉曼光作用下,靠近中心速度处原子被激发跃迁(白色表示)。图4(c)描述了第一个π 脉冲周期时刻,不同速度原子的跃迁概率分布。
由于脉冲持续时间内,原子速度的增加,原子感受到的激光频率在相互作用过程中发生了改变,导致跃迁到2 态原子的中心速度也相应发生了改变,偏移量为-0.24kħ(如图4(c)所示,文中动量单位统一取单光子反冲动量kħ)。由拉曼脉冲速度选择效应所决定的,跃迁原子的动量分布半峰宽度为,FWHM=0.37kħ,可见即便在极短的脉冲持续时间内(10μs 量级),由重力加速度g 造成的原子速度改变,进而引起的多普勒频移效果也是不可忽视的。
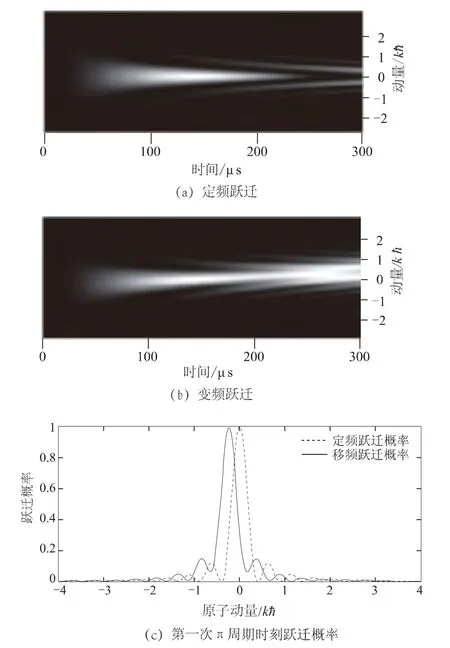
图4 存在频移时原子的拉比振荡
我们以拉曼脉冲型重力仪中的典型干涉操作为例进行分析。当原子经拉曼速度选择被挑选出来后,设中心速度为0,20 ms 后作用π/2 脉冲,100 ms 后作用π 脉冲,再经100 ms 后作用第二束π/2 脉冲完成干涉。原子团速度变化如图5所示。按照原子自由落体过程补偿多普勒频移,则在第一个π/2 脉冲起始时刻的激光多普勒频移补偿对应速度为20 ms·g,π 脉冲起始时刻的多普勒频移补偿对应速度为120 ms·g,第二个π/2 脉冲时刻激光多普勒频移补偿对应速度为220 ms·g。
按照普遍情况,设计脉冲持续时间为10 μs 量级。按上述的数值计算方法,对不同速度原子跃迁概率进行计算。当原子经过速度选择后,分布如图5(a)a1。
首先,原子团经π/2 脉冲激励拉比振荡跃迁,1态、2 态原子跃迁概率如图5(a)中a2 和a3,各自偏移-0.12kħ。末态原子数量分布如图5(a)中a3,1 态原子中心速度比无啁啾偏大,2 态原子正好相反,两态原子分布与定频脉冲基本保持一致。
在上个脉冲末态的基础上(初始原子分布如图5(b)中的b1),再经π 脉冲作用,1,2 态跃迁概率各自偏移中心速度(动量)-0.24kħ,如图5(b)中b2,最终原子分部如图5(b)中b3。易见,1,2 两态的有效原子数量个下降约1/2,且中心速度偏离虚线所示的定频模式。
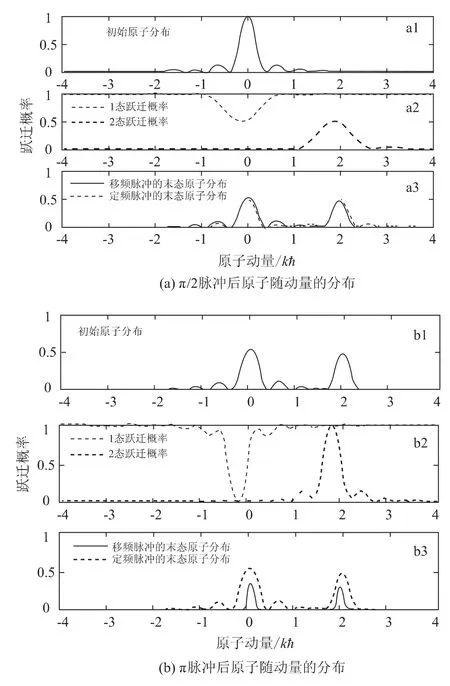
图5 有效原子在动量上的分布率
由上述分析可见,经过拉曼光分束、翻转后的有效原子,在中心速度附近的总数量下降了50%左右。另外,两条路径最终干涉时的原子数量也存在明显的数量差,占中心速度处总原子数约34%-30%=4%,因此,两条路径分束干涉仍将再次损失8% 左右对比度。
3 结论
由于脉冲持续时间内(10 μs 量级)的多普勒频移,原子团中心速度改变,大量原子偏离拉曼光作用范围,造成有效原子损失;另外,干涉两路的原子数量也产生了差别,两者共同导致干涉条纹对比度理论下降约60%。本文仅就有效原子数量这一个角度,估算了原子干涉条纹对比度在拉曼光不能补偿脉冲持续时间内多普勒频移的情况,最终的条纹对比度、测量灵敏度以及系统误差还应考虑频率啁啾造成的相移等因素。可以推测,实际综合测量能力的降低,有可能远超60%。因此,拉曼光作用时间内的多普勒频效应不能忽略;如果采用定频拉曼激光,应通过本文给出的数值方法,对激光的中心频率点位置,及多普勒频移进行精确计算补偿。
[1]DickersonS M,Hogan J M,Sugarbaker A,et al.Multiaxis Inertial Sensing with Long-Time Point Source Atom Interferometry[J].Physics Review Letters,2013,111(8):083001.
[2]Torsten Petelski.Atom Interferometers for precision gravity measurements[D].Paris:Université Paris 6,2005.
[3]周敏康.原子干涉重力测量原理性实验研究[D].武汉:华中科技大学,2011.
[4]徐周翔.冷原子干涉实验的激光频率以及过程的自动控制[D].杭州:浙江大学,2012.
[5]KasevichMark,Chu Steven.Atomic interferometry using stimulated Raman transitions[J].Physics Review Letters,1991,67(2):181-184.
[6]王义遒.原子的的激光冷却与陷俘[M].北京:北京大学出版社,2007.
[7]PetersA,Chung K Y,Chu S.High-precision gravity measurements using atom interferometry[J].Metrologia,2001,38(1):25-61.
[8]Kathryn Moler,David S.Weiss,Mark Kaservich,et al.Theoretical analysis of velocity-selective Raman transitions[J].Physics Review Letters,1992,45(1):342-348.

