±500kV 同塔双回直流输电线路的电晕损失分析

范军华

（中国南方电网超高压输电公司广州局，广东 广州510670）

0 引言

国家经济的快速发展对电力建设提出了更高的要求。高压直流输电不仅造价低、可靠性高，还具有调节快速、电能损失小等优点，从而在长距离架空输电、海底输电等场合得到了广泛使用。而同塔双回直流输电线路不仅具有单回线路的优点，还能够实现单位面积走廊上线路输电能力的提升以及占用土地的减少，从而有效提高电力建设水平［1］。

线路的电晕会产生电晕损失，带来电能损失，从而增加输电成本。虽然不能够完全消除线路电晕，但可以通过改变极导线的排列方式、增加导线尺寸等手段来减少电晕损失，从而实现更好的经济效益。本文通过分析500kV 同塔双回直流输电线路的极导线在不同排列方式下的电晕损失，选出最优排列方式，希望能为工程建设提供有益参考。

1 计算方法

直流线路电晕损失的计算方法分为两种［2］：数值计算法和经验计算法。

1.1 数值计算法

假设导线周围分布着N 根电力线，对于导线表面的任意一点而言，电力线在其上所产生的电荷浓度分别为ρ＋和ρ－，那么，这点的电流密度J 为：

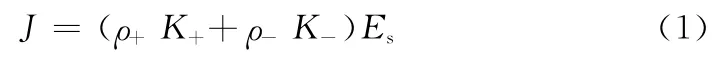
式中，K＋和K－分别为正负离子的迁移率；Es为空间电荷影响下地面合成场强。

根据式（1）就可得到每根电力线在导线表面起始点的电流密度，通过对电流密度进行积分，就可得到流入或流出导线的总电流。令每根导线的电压与总电流分别为｛Ui｝i≥1和｛Ii｝i≥1，那么线路总的电晕损失P 为：

1.2 经验计算法

Anneberg公式是在大量实验数据基础上总结出的一种计算良好天气下直流线路电晕损耗的经验公式，其表达式为：

2 仿真场景

图1给出了±500kV 同塔双回直流输电线路的极导线排列方式。从图1可以看出，4种方式极导线的相对位置不同，这将会影响导线表面的电场强度，从而造成线路电晕损失的不同。为便于分析线路的电晕损失，本文假设了如表1和表2所示的计算条件。

图1 极导线的.种排列方式

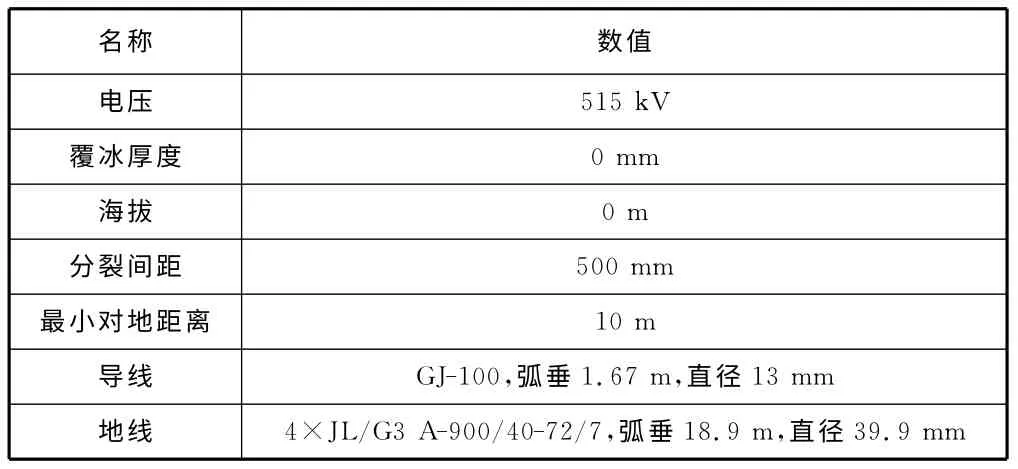
表1 计算条件

表2 线路空间坐标

3 电晕损失计算

经计算，方式A、B、C 和D 的地线表面电场强度分别为9.1kV/cm、13.5kV/cm、25.6kV/cm、25.6kV/cm。方 式A的电场强度是最低的，这是由于在方式A 中，极性不同的导线是错位排列，从而有助于电场的相互消除。虽然方式B 的同极性导线都位于线路同一侧，但离地线最近的极导线极性是相反的，因此，其电场强度仍低于方式C 和方式D。由Peek公式可知，地线起晕场强为20.6kV/cm，而方式C和方式D 的电场强度都大于20.6kV/cm。虽然通过增加极导线和地线的距离或增粗地线能够降低方式C 和方式D 的电场强度，使其低于20.6kV/cm，但上述方式会额外增加铁塔重量或地线重量，因此在实际应用中并不使用方式C 和方式D。故以下计算电晕损失时，仅计算方式A 和方式B。

3.1 经验计算法

图2（a）给出了方式A 的电晕损失图，从图中可以看出，方式A 的电晕损失PA是由上层回路电晕损失P1、下层回路电晕损失P2和回路间电晕损失P3构成。

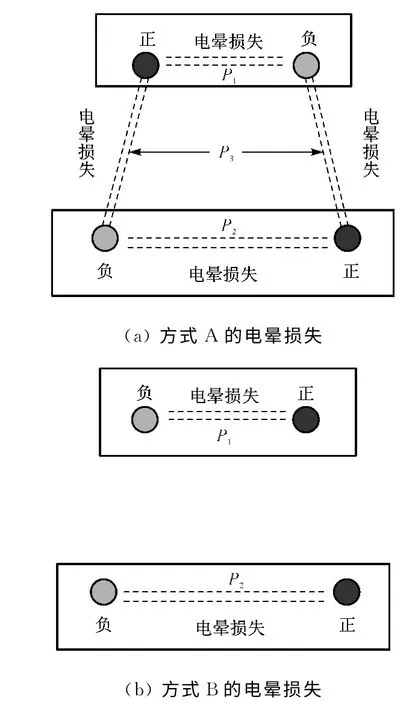
图2 方式A和方式B 的电晕损失图

根据式（3）可得：

根据式（3）可得：

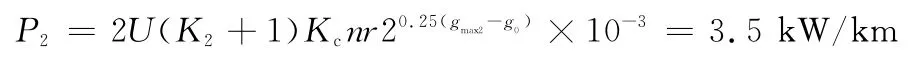
同理：

其中，K ＝K1，gmax＝（gmax1＋gmax2）/2。

因此，PA＝P1＋P2＋P3＝9.8kW/km。

图2（b）给出了方式B的电晕损失图，从图中可以看出，方式B的电晕损失PB仅由上层回路电晕损失P1和下层回路电晕损 失P2构成。根据式（3）可得，P1＝2.07 kW/km，P2＝2.09kW/km，那 么PB＝P1＋P2≈4.2kW/km。由此可以看出，方式A 的电晕损失要高于方式B。

3.2 数值计算法

在第2节的仿真场景设定下，方式A 和方式B在不同粗糙系数下的电晕损失如表3所示。从表3可以看出，方式B 的电晕损失始终小于方式A 的，并且随着粗糙系数变大，两种方式的电晕损失都变小。

表3 数值计算法下方式A和方式B的电晕损失

4 结论

根据以上计算结果可知，方式B 的电晕损耗要小于方式A。因此，在实际使用中应采用方式B的排列方式，从而达到减少能耗的目的。

［1］别睿，涂莉，周全，等.同塔双回直流输电线路的感应电压仿真研究［J］.陕西电力，2014，42（5）：11－16.

［2］Parekh H，Chow Y L，Srivastava K D.A Simple Method of Calculating Corona Loss on Unipolar DC Transmission Lines［J］.IEEE Transactions on Electrical Insulation，1980，15（6）：455－460.