含微型燃气涡轮机的中低压微电网动态仿真

霍雪松 李云鹏

（1.国网江苏省电力公司，江苏 南京210024；2.国网南通供电公司，江苏 南通226001）

0 引言

近年来，分布式发电系统并网运行相关理论与技术研究日益受到关注。微电网作为一种新型的电力系统，连接着低压配电网的诸多小型模块，可有效解决分布式电源对电网的影响。微电网存在两种典型的运行模式：正常情况下微电网与常规配电网并网运行，称为联网模式；当检测到电网故障或电能质量不满足要求时，微电网将及时与电网断开而独立运行，称为孤岛模式［1］。微型发电机是功率小于100kW 的小单元，并且绝大部分包含电力电子接口，主要使用可再生能源或者矿物燃料［2］，在当地热电联产模式中应用。微电网技术可以有效缓解当前的能源危机，对于自然环境的保护和经济、社会、生态的可持续发展来说至关重要。

当微电网使用单相电路并配单相负载时，微电网与包括感应电动机在内的动态负载相互作用会出现一些不平衡的状况［3］，这就给电力系统的安全稳定运行带来了不利。对于微电网运行的稳态模型和动态模型，有必要进行系统的研究。为了模拟这些效果，分析工具必须能模拟系统的三相状况、中性线、地面指挥和接地线路。该工具应当具备稳态和动态模型，以应对多种形式的微电源和其接口［4］。

本文介绍了用于均匀三相感应发电机、微型燃气涡轮机和风力发电机的模型［5－6］，单相感应发电机、光伏系统、燃料电池、电网侧逆变器和其他模型被集成在仿真平台中［7－8］。本文展示了微电源模型和发展于微电网项目框架的仿真平台，该平台可以对包含微型发电机的低压三相网络的稳态和动态操作进行仿真，这涉及到充足的微电源、机器（感应电机和同步电机）和逆变器模型在毫秒时间内的发展。通常，这些设备被直接耦合到电网，因而对电网电压和频率产生直接影响。用于分析的仿真工具能够表现微电网在光伏并网和独立操作过程中的动态行为，包括平衡状态和不平衡状态。

1 微电源模型

1.1 三相对称感应发电机

感应发电机在任意参考系中都是用四阶模型来表示，采用发电机惯例的定子电流：

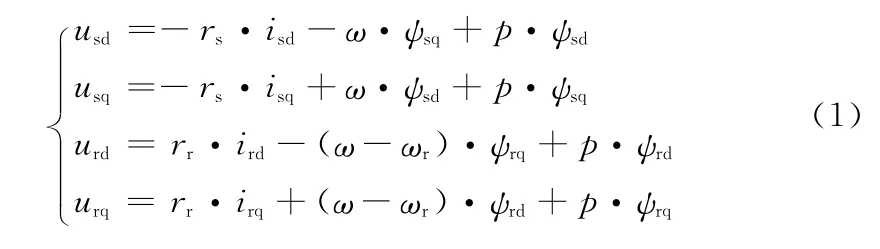
通量与定子、转子绕组电流有关，关系如下：

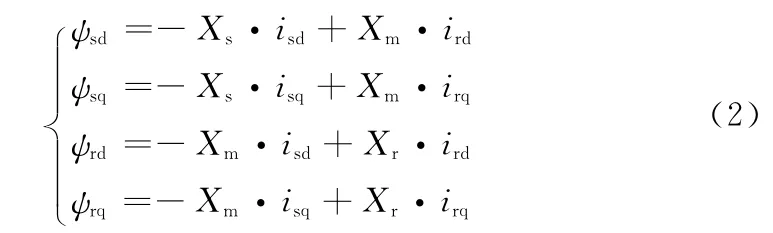
电磁转矩表达式如下：

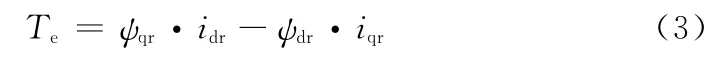
1.2 微型燃气涡轮机

微型燃气涡轮机通常指输出范围为25～300kW 的小而简单循环的燃气涡轮机，它们是燃气涡轮机技术演变的一部分。在典型的微型燃气涡轮机设计中，该微型发电系统包括涡轮、换热器、发电机和电力电子设备。

本研究中主要关注的是网络的动态特性，采用的微型燃气涡轮机模型基于以下假设：（1）换热器不包含在模型中；（2）燃气涡轮机的温度控制和加速控制对正常工作条件没有影响。

图1是分析微型燃气涡轮机负荷动态行为的简化框图。实际功率控制可以被描述成一个比例积分（PI）控制功能，图1中，Pdem是要求的功率，Pref是基准功率，Pin是施加到所述涡轮机的功率控制变量，Kp是比例增益，Ki是PI控制器的积分增益。

图1 微型燃气涡轮机的主要模块与负荷跟踪控制系统

图2为GAST 涡轮机模型，Pin是机械功率，Dtur是涡轮机的阻尼，T1是燃油系统滞后时间常数1，T2是燃油系统滞后时间常数2，T3是负载极限时间常数，Lmax是负载限度，KT是温度控制回路增益。

1.3 风力发电机

风力发电机包含几个独立建模的子系统，子系统的设计基于空气动力学和机械动力学等理论。其中，变速率风力发电机还涉及发电机和功率转换器系统。下面是各子系统的模型介绍。

图2 涡轮机模型

1.3.1 空气动力学系统

空气动力系数曲线被用于叶片动力学的研究：

式中，Pa为气动功率；ωr为叶片旋转速度；Tw为气动扭矩；ρ为空气密度；A 为转子区域，A＝πR2；Cp（λ，β）为无量纲的性能系数，λ为叶尖速比，β为桨距角；vw为风速。

1.3.2 机械子系统

可以选择3个或者6个弹性相连的质量等价物用于模拟风力发电机的机械系统，对于低速轴扭转模式，至少需要使用2个质量等价物，下式是系统使用3个质量等价物的状态空间方程：

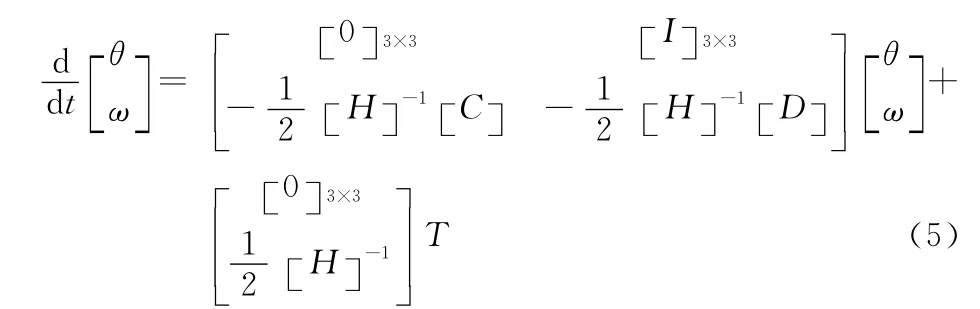
式中，θT＝ ［θR，θGB，θG］，为角位置矢量；ωT＝ ［ωR，ωGB，ωG］，为角速度矢量；TT＝ ［TW，0，TG］，为外转矩矢量，由空气动力学和电磁转矩组成；［0］3×3和［I］3×3分别为三阶零矩阵和单位矩阵；［H ］＝diag （HR，HGB，HG）是只保留对角线的矩阵；C是刚度矩阵；D 是阻尼矩阵。

C 矩阵代表高低速轴的弹性，定义如下：

D 矩阵代表内摩擦损耗和转矩损失，定义为：

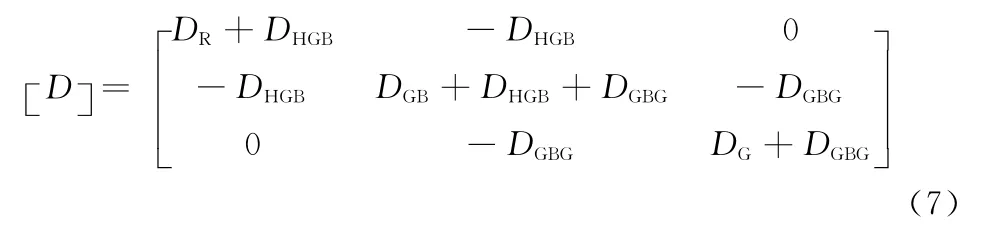
其中，下标｛H｝、｛GB｝、｛G｝分别表示风机叶片、变速箱和发电机。弹性系数矩阵C 中，CHGB表示风机叶片和变速箱之间的弹性系数，CGBG表示变速箱和发电机之间的弹性系数；阻尼矩阵D 中，DR、DGB、DG分别代表3个质量块的自阻尼系数，其余为相互之间的互阻尼系数。

2 仿真平台构建

在微电网实现的低压网络中，导体的电阻比电抗大，单相线路配单相负载时，微电网与感应电动机不平衡，可以将低压网络从整个网络中区分开来。

一个典型的符合拥有三相和中性线的线路或电缆的网络构建如图3所示。

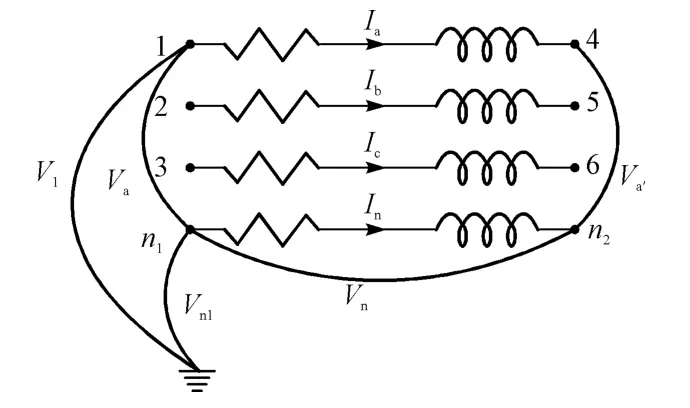
图3 微电网低电压馈线实例

a相的基尔霍夫方程可以记作：

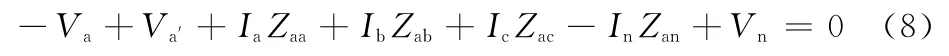
考虑到Vn＝ （Ia＋Ib＋Ic）Zn，为了简化，a相的网格方程省略互耦参数，得到如下方程：

据此，我们得到其他两相和反相方程，最终得到包含联系三相电流与电压的中性线的导纳形式的方程：

式中，Yabc（n）是原始导纳矩阵，字母n表示中性线也包含其中；电压下标表示节点之间的电势差。

以电流注入作为分支电流，分支电压作为节点电压，可以得到如下两式：

结合方程组（10）、（11）、（12），得到线路或电缆的节点方程：

如果连接或关联矩阵A 可以写成2个三阶单位矩阵AT＝［I －I］ ，那么节点方程可以记作：

含有4条导线的线路或电缆被看成一个含有负荷分支导纳Yabc（n）的整体。利用这种方法代替各个四线制的线路，关联矩阵用三阶单位矩阵表示，结合节点导纳矩阵，以此来建立网络方程。如果我们用同样的方法处理复合支路导纳，用单导纳来表示网络的过程是一样的，用星形连接的恒阻抗负荷将有如下形式的复合导纳：

中低压变压器的建模遵循类似的程序，在这种情况下，关联矩阵A 展示了相互耦合的分值是联系在一起的。不考虑电源定子的瞬态，定子阻抗变为网络的一部分，并且电源看作是电抗后的电动势，例如旋转电机的瞬时电压在瞬时电抗后面。每个时间步，电动势的大小和相角都会作为网络的输出被微分方程求出。特别要说的是，对于3 匹或者1 匹的电压逆变器，需要的大小和相角是指a相的大小和相角——Ea∠θe（t），其中，相角θe（t）为：

这和在固定框架下提供Ed和Eq一样，只需要d轴对准a相轴，因为它也是旋转机械直接耦合到电网的情况。网络代数方程的解返回到电源，定子的正序电流和为了控制而需要的其他值作为下一次迭代时的初值，例如定子终端电压。

显然，在只考虑正序分量的情况下，电源提供的内部电势是平衡的，因此，求取时域解只是为了求得正序分量值。考虑负序分量时，假定电源只与其负序阻抗作用，因而网络导纳矩阵中包含定子阻抗。

整个仿真工具建立于Matlab和Simulink，采用频域表示（向量法）以提高仿真效率，合理处理中性线并使用自然相量（a—b—c）。微电源和动态负载通过其“定子阻抗后面的电动势”等效接到网络求解器，电网、负载和电源的不平衡可以被简单处理。

3 微电网运行仿真测试

所有的仿真都涉及一个低电压网络研究案例，其节点带有电源。考虑的干扰包括突然从主网脱落、负载改变、网络单元（电池逆变器）的缺失和非可调电源产量水平的改变。

图4是一个低电压网络研究案例，用来测试仿真工具的性能。

利用仿真工具对许多干扰信号都进行了检查，主要包括以下几个方面：（1）从主电网隔离；（2）微电网负荷的逐步改变；（3）分散电源产量的改变；（4）电网形成单元的损失（电池逆变器）。

从仿真结果中选出典型的图作分析，图5、图6和图7分别是电网在0.8s断开时，电池逆变器产量的改变、电网供应电缆的电流和负载节点的相电压，图中，有功功率P 和无功功率Q分别用实线和虚线表示。

仿真工具已经建立了网络解算器代码，仿真基于Matlab运行，它能解决稳定状态和动态条件下的平衡和不平衡问题。

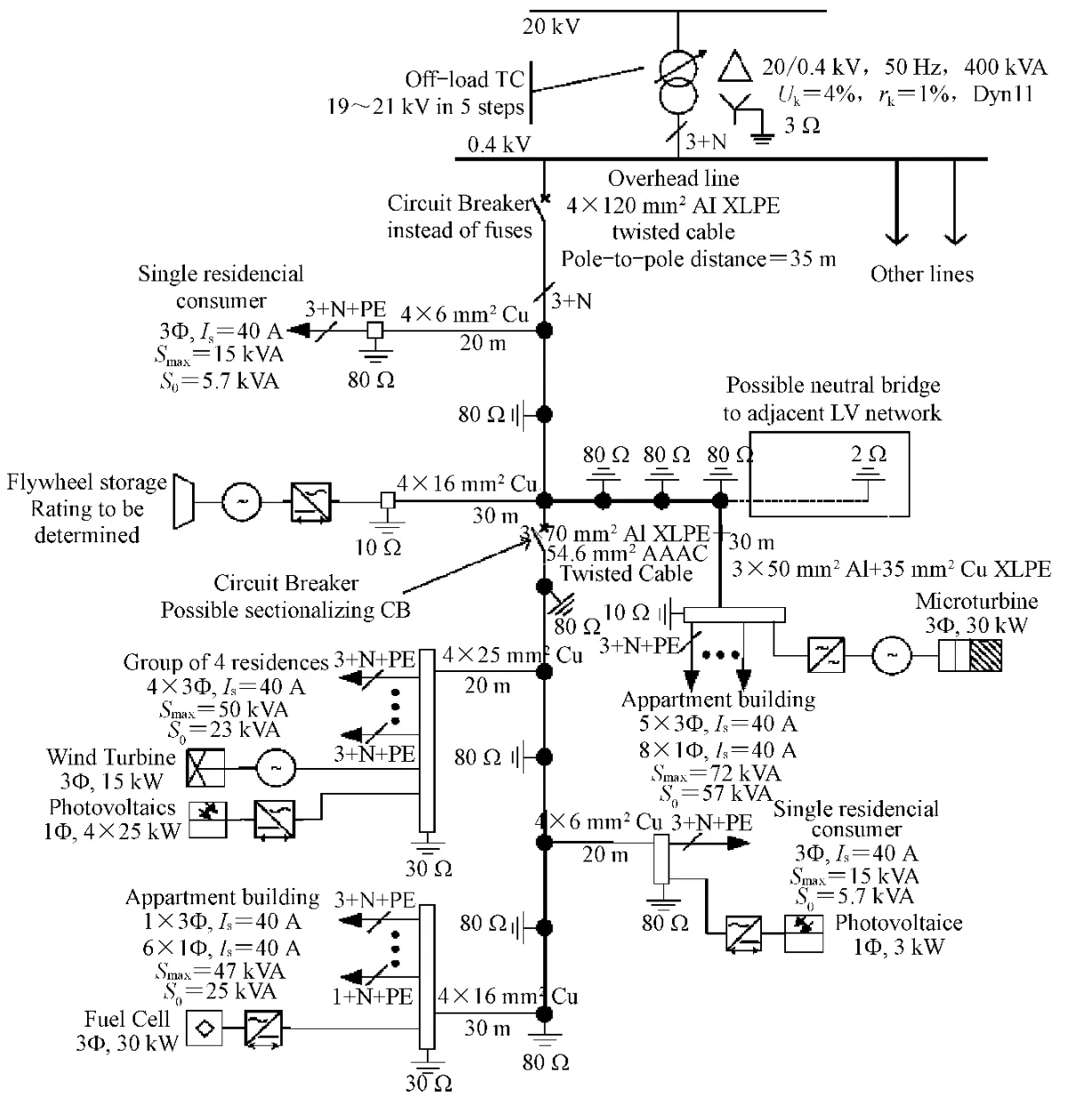
图4 微电网低压系统研究案例

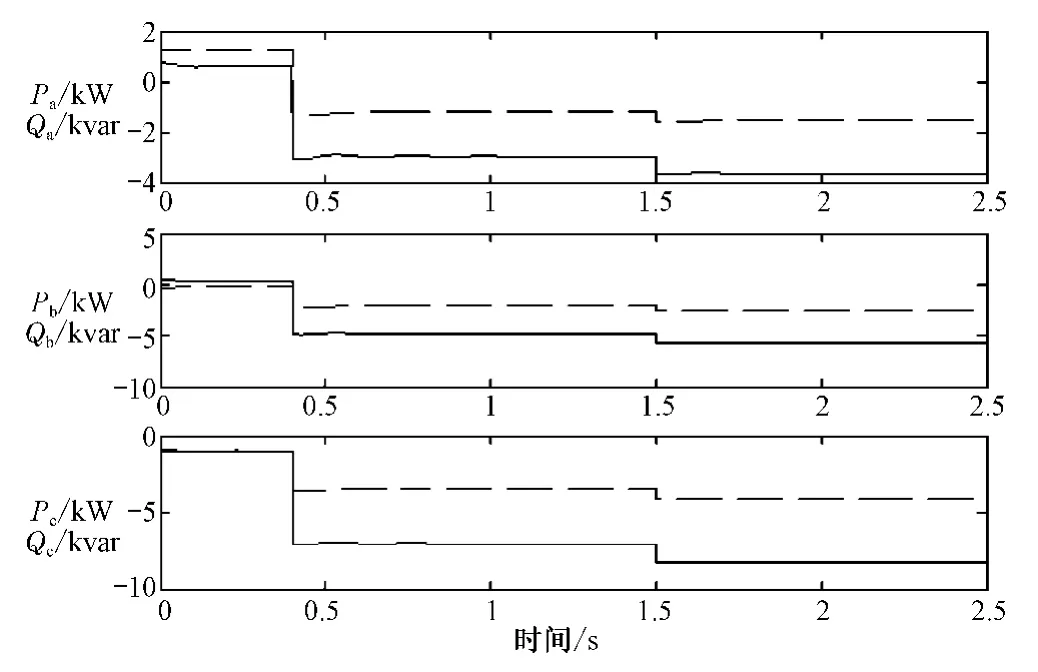
图5 电池逆变器产量的改变

图6 电网供应电缆的电流变化

图7 负载节点的相电压变化

4 结语

对于微电网并网的稳定运行和动态运行问题，传统的手段很难进行分析和解决，本文利用仿真技术，对中低压微电网进行模拟运行和验证，结果表明了仿真平台的有效性。仿真工具建立的解算器代码已经在多种网络环境和干扰条件下测试过，其完善性也在案例中得到证实。在仿真过程中，电网、负载和电源的不平衡可以被简单处理了，这可能会带来一些误差，在后续研究中要合理考虑这些因素。

［1］彭克，王成山，李琰，等.典型中低压微电网算例系统设计［J］.电力系统自动化，2011，35（18）：31－35.

［2］王成山，高菲，李鹏，等.可再生能源与分布式发电接入技术欧盟研究项目述评［J］.南方电网技术，2008，2（6）：1－6.

［3］李鹏.分布式发电微网系统暂态仿真方法研究［D］.天津：天津大学，2010.

［4］王小单.微网建模及电磁暂态仿真研究［D］.武汉：华中科技大学，2012.

［5］闫根弟.动态电力系统数字仿真模型的研究［D］.太原：太原理工大学，2005.

［6］许寅，陈颖，梅生伟.风力发电机组暂态仿真模型［J］.电力系统自动化，2011（9）：100－107.

［7］Hatziargyriou N，Kariniotakis G，Jenkins N，et al.Modelling of micro－sources for security studies［C］//CD－Rom Proceedings of the 2004CIGRE Session.Paris，2004.

［8］徐青山，孙鄞，丁茂生，等.采用下垂控制的微电网小干扰稳定性分析［J］.华南理工大学学报：自然科学版，2013，41（12）：56－62.