复杂高层建筑结构TLD 减震数值模拟①

徐龙江

(上海同设建筑设计院有限公司，上海200092)

0 引 言

由于环境振动及地震地面运动引起的建筑物结构水平振动导致居住在内的居民舒适感降低的例子在近些年出现不少，迫切需要寻找一种经济、安全且可行的解决办法.已有学者对调频液态阻尼器(简称TLD)在高层建筑结构振动控制中做过研究［1］，结果表明，在TLD 选择理想的情况下，对建筑结构水平振动有很好的控制作用.本文在以上研究结果的基础上，以一幢带裙房的大型复杂具有低频自振周期的结构为对象，选取不同卓越频率的地震波对安装TLD 和未安装TLD 的结构模型进行了动力时程分析，在对比分析结果数据的基础上，论证TLD 的减振效果及可行性.

1 TLD 原理简介

TLD(Tuned Liquid Dampers)是利用装在水箱或者容器内的流体，在目标物体发生晃动或者震动的时候，流体惯性作用下，与目标减振物体产生相反方向的运动而达到耗能减振的目的［2］.TLD 受底部传来的激励时，其晃动耗能示意图见图1 所示，其原理是内部晃动的流体与结构形成反向共振，达到耗能减振的目的.当结构带动TLD 一起沿x 向运动时，TLD 内水体晃动形成波浪，对水箱壁产生动水压力即构成了对结构的减振力，y 向同理.一般将TLD 中液体的第一阶自振频率调至结构需要控制方向的第一阶自振频率的95% ～98%，才会取得最满意的控制效果.此外，TLD 中流体质量需达到所需控制结构模态有效参与质量的1%～3%才能发挥最大的减振效果.根据容器的形状、大小以及内部液面的高低来调节两个水平方向的震荡频率与被控制结构两个主方向的自振频率一致，以达到结构双向减振的目的.假定，TLD 容器为矩形容器，其两个方向的尺寸分别为L 和B，液面禁禁止时候的高度为h，长边边长L 与短边边长B 之比小于8 时，TLD 振荡的第一阶振荡频率为可由下式计算.图2 给出了TLD 不同宽度a 对应的f与TLD 静止液面高度h 关系曲线.

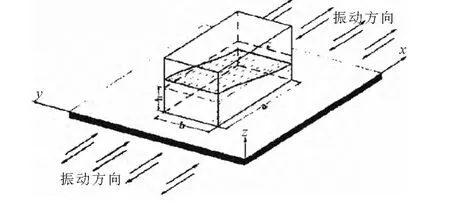
图1 TLD 耗能减震示意图

2 工程概况及有限元模型的建立

2.1 工程概况

该高层模型位于某市，是一个集高档公寓、商业于一体的高层建筑，其中裙房4 层.工程总建筑面积25980m2.主楼地上22 层，总高度约80m.地下层为消防池、泵房、柴油发电机房、锅炉房等设备用房和汽车库;1 ～4 层为大空间商业用房，包括超市、健身会所、餐饮等，层高为4.20m;5 ～22 层建筑面积18800m2，为商务住宅用房，层高为3.30m.

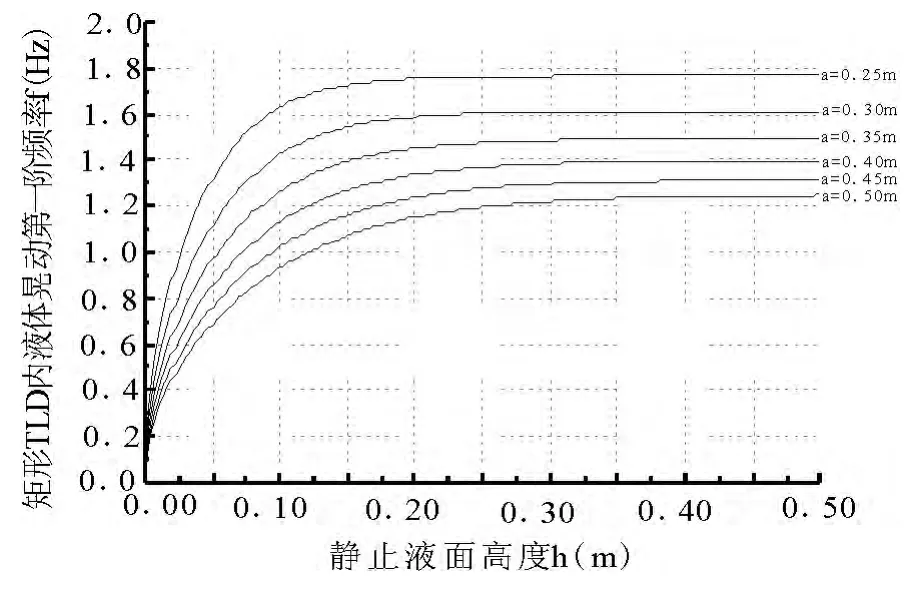
图2 TLD 第一阶自振频率随液面高度的变化曲线

图3 结构三维有限元数值模型

图4 结构的前四阶振型图

主楼抗侧力体系为现浇钢筋混凝土框架－剪力墙结构，楼、屋盖结构为现浇钢筋混凝土主次梁板.该结构高宽比为3.93，接近《高层建筑混凝土结构技术规程》对A 级高度钢筋混凝土框架剪力墙结构的最大高宽比最大为4 的规定［3］.

图5 本文选用的4 条地震波时程曲线

2.2 基本参数及有限元模型的建立

结构分析采用主楼的三维整体计算分析模型，主体结构采用框架－剪力墙结构，楼面为普通的混凝土梁板体系.建筑抗震设防烈度为8 度，场地类别为Ⅲ类，设计地震分组为第一组，设计基本加速度为0.20g，场地土的特征周期0.35s，结构的阻尼比为0.05.

采用大型通用有限元计算软件ANSYS 对该复杂高层建筑结构进行建模.采用beam188 梁单元模拟柱子和梁且均选择矩形截面，1 ～4 层柱截面选择900mm×900mm，5 ～22 层柱截面选择700mm×700mm.楼层梁截面可以根据具体的位置不同而选择450mm×700mm，400mm×700mm，350mm×700mm 三种截面.楼板和剪力墙结构采用壳单元Shell63 来模拟.模型共采用4854 个空间梁单元和1848 个壳单元.有限元模型如图3 所示，结构构件截面特性如表1 所示.

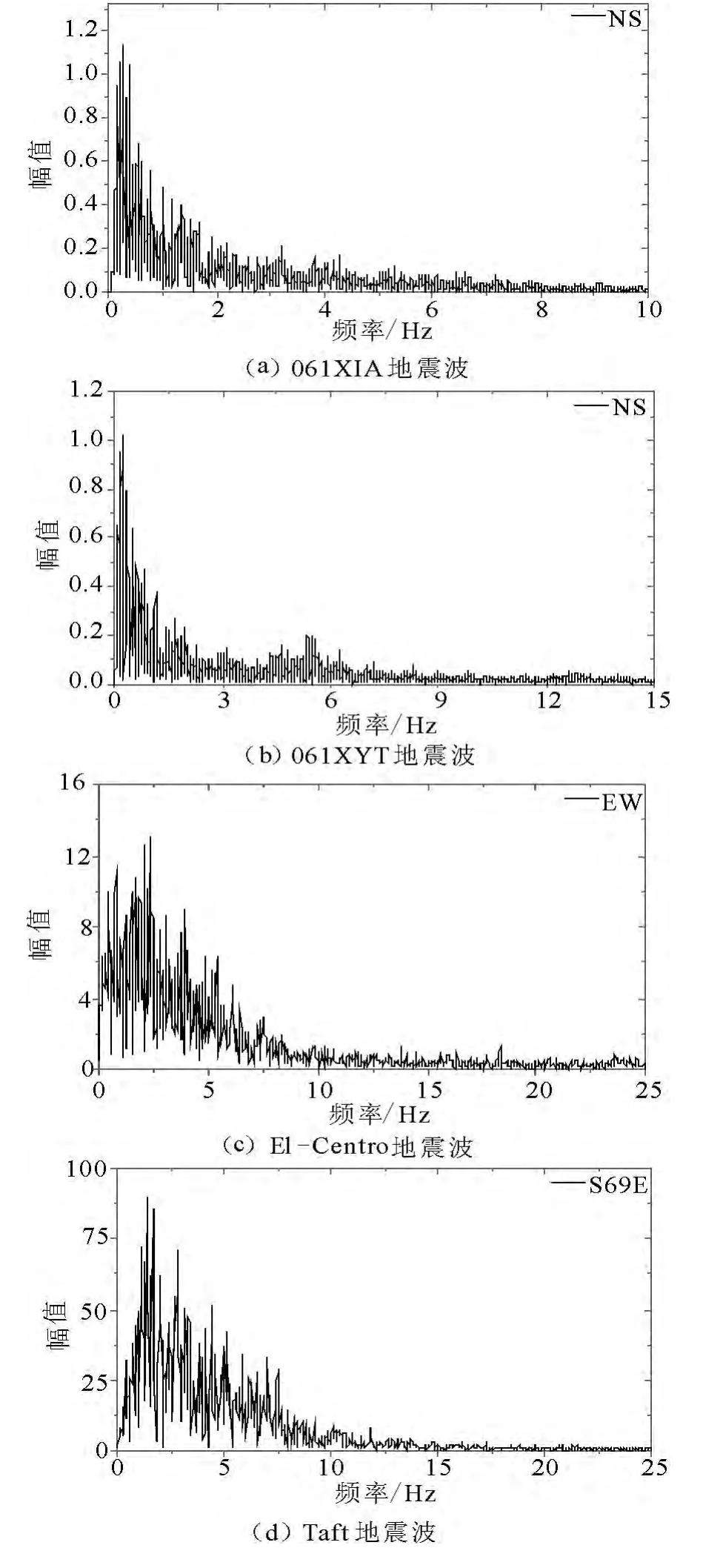
图6 对应4 条地震波傅里叶谱

2.3 有限元模型动力特性分析

采用ANSYS 分析软件中的Lanczos 法进行结构动力特性分析［4］，求取结构前20 阶自振频率，见表1 所示.图4 列出了结构前四阶振型图.

表1 结构动力特性

由以上图表可以看出，结构第1 阶振型为Y 方向水平振动，第2 阶振型为X 方向水平振动，第三阶振型扭转振动，第四阶振型为局部振动.前两阶结构自振周期较为接近，说明结构两个方向抗侧力刚度基本一直.结构以平动为主的第一自振周期2.11s，以扭转为主的第一自振周期Tt=1.82s，其比值Tt/T1 =0.86，略大于规范对周期比规定的限值0.85 的要求，说明结构的扭转效应较明显，但具有足够的抗扭刚度.

图7 对应4 条地震波反应谱

3 结构地震反应分析

3.1 输入地震波的选取

为了分析不同类型地震波对复杂高层结构的地震反应影响，本文分别从2008 年墨汶川8.0 级大地震中选取2 条具有典型长周期信息的地震波(台站编号为:061XIA 和061XYT)进行分析，并选取1940 年美国Imperial Valley 地震时记录到的EL－Centro 地震波和1952 年美国加利福尼亚Kern County 地震时记录到的Taft 地震波作为常用普通地震波作对比参考.图5 为所选的4 条地震波加速度时程图.

3.2 地震波的频谱特性分析

地震记录的频谱分布对结构的响应有很大影响，可以从傅里叶谱和反应谱显现出来.分别计算所选4 条地震波的傅里叶谱和反应谱，分别见图6和图7.

对比长周期地震波和普通地震波的傅里叶谱可以看出，长周期地震波的频带较普通地震波的频带更低，主要分布在下雨2Hz 的范围内，长周期特征表现得更明显;两条普通地震波高频成分都比较丰富，主要分布在1 ～6Hz，频带分布集中在相对较高的频率部分.

从四条地震波的反应谱可以看出，长周期地震波在长周期部分明显比两条普通地震波的谱值要大，即向长周期部分延伸，对应的谱值集中在0 ～7秒内，分布比较广泛.而普通地震波对应的谱值主要集中在0 ～2 秒内，对短周期结构地震反应影响较大.

3.3 结构动力反应分析

分别以前面4 条地震波(两条长周期地震波和两条普通地震波)作为输入激励，对第二节所建立的有限元数值模型进行动力时程反应分析，分析过程中，阻尼模型选取工程上常用的瑞丽阻尼模型［5］，取结构第一阶自振频率和输入激励的卓越频率为瑞丽阻尼的控制频率，整体结构的阻尼比取为5%.

图8 结构在地震作用下最大响应图

分别选取楼层水平加速度放大系数、楼层最大 位移、楼层最大剪力和楼层最大弯矩作为参考变量，对不同频谱特性地震波作用下的结构响应进行 了分析对比，具体结果见图8.

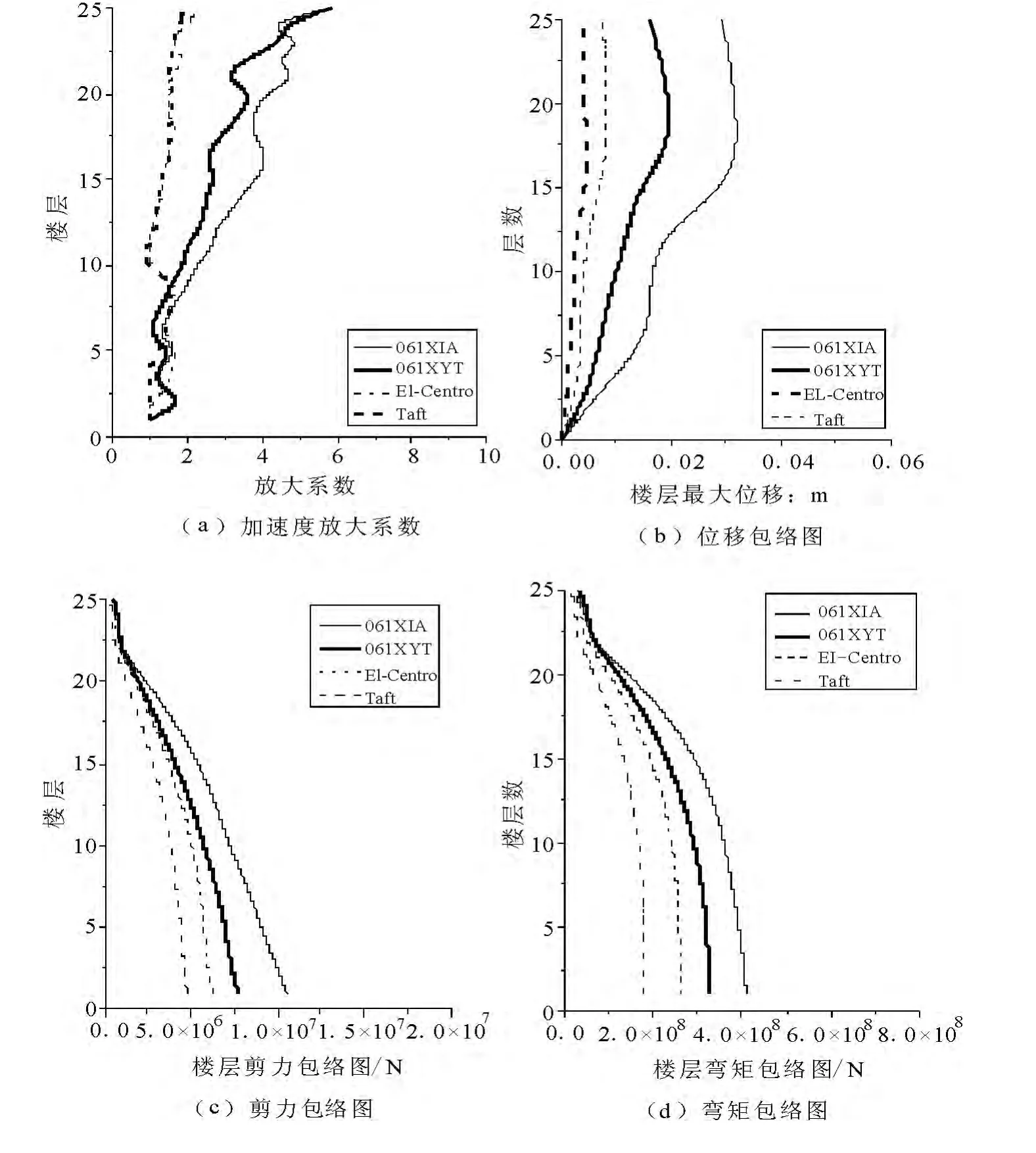
图9 结构在地震作用下最大响应图

对比不同地震波作用下结构的最大响应，可以看出，不同类型地震波作用下，结构的最大响应有显著的不同:结构在具有长周期特征的地震波作用下高层结构的位移响应值、加速度响应值和内力响应值均明显大于普通地震波作用下的结果;两者对应的结构最大位移响应相差达5 倍左右，最大加速度响应相差约3 倍左右，基底剪力平均值和弯矩平均值相差1 倍左右.

4 结构TLD 减震效果分析

TLD 方案的确定

由第二节模态分析结果可以看出，结构沿东西方向第一阶自振频率为0.47Hz，结构沿南北方向的第一阶自振频率为0.50Hz;根据TLD 减震原理，将TLD 水箱两个方向的自振频率调整到与结构的两个水平方向自振频率相接近，以达到同时对结构两个方向振动控制的目的.本文采用ANSYS 有限元软件中的Fluid80 单元模拟TLD 流体.

为了对比分析TLD 减震效果，分别将前面4条地震波(两条长周期地震波和两条普通地震波)作为输入激励，对第二节所建立的有限元数值模型添加TLD 后进行动力时程反应分析，分别选取楼层水平加速度放大系数、楼层最大位移、楼层最大剪力和楼层最大弯矩作为参考变量，对不同频谱特性地震波作用下的结构响应进行了分析对比，具体结果见图9，TLD 减震前后的结果地震反应对比误差见表2.

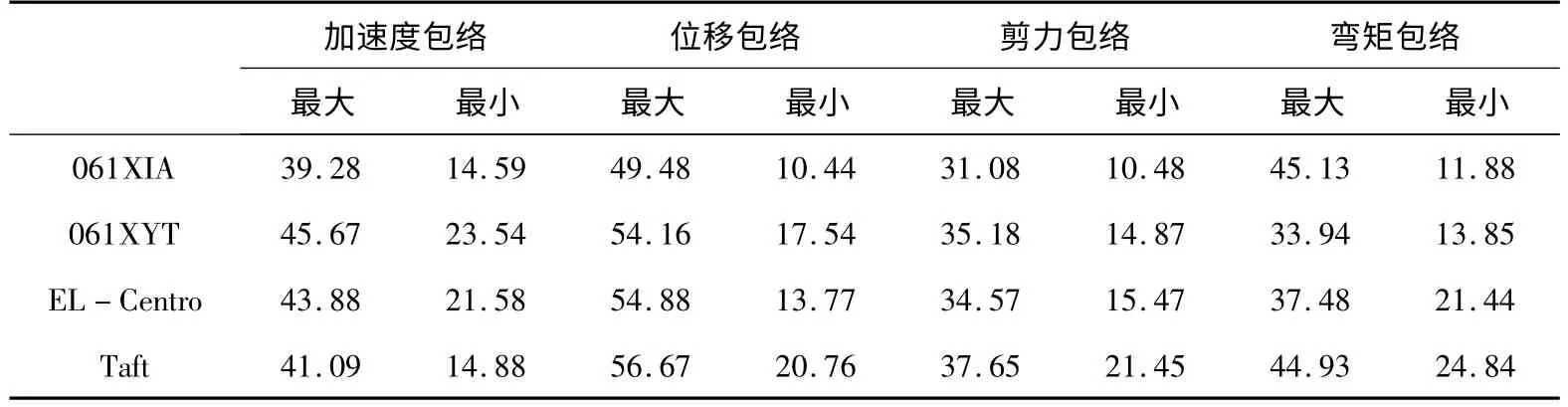
表2 TLD 减震前后结构地震反应相对误差(%)

从以上图表的对比可以看出，TLD 减震效果比较明显，最大减震效果达到与60%;不同类型地震波作用下，结构减震效果有明显的不同.对比不同响应之间的减震效果，可以看出，TLD 对加速度和位移的减震效果要明显大于对剪力和弯矩的减震效果，由此可以看出，TLD 在结构水平方向振动控制、提高居民居住舒适度上有很好的控制效果.

5 结 论

本文在将TLD 减震控制应用于一幢带裙房的大型复杂结构振动控制中，以数值模拟为手段，采用动力时程分析方法，选取不同卓越频率的地震波对安装TLD 和未安装TLD 的结构模型进行了动力时程分析，在对比分析结果数据的基础上，论证TLD 的减振效果及可行性.具体结论如下:

(1)可以通过合理控制TLD 水箱两个方向的尺寸及内装液体的液面高度，可以达到同时对结构两个水平方向振动控制的目的，一般将TLD 中液体的第一阶自振频率调至结构需要控制方向的第一阶自振频率的95%～98%，才会取得最满意的控制效果.

(2)本文复杂高层结构在具有长周期特征的地震波作用下高层结构的位移响应值、加速度响应值和内力响应值均明显大于普通地震波作用下的结果;两者对应的结构最大位移响应相差达5 倍左右，最大加速度响应相差约3 倍左右，基底剪力平均值和弯矩平均值相差1 倍左右.

(3)通过对安装TLD 和未安装TLD 的模型地震反应结果对比分析可以看出，TLD 对于结构两个水平方向的振动控制都有良好的控制效果，

［1］ 韩博宇.TLD 应用于不同自振特性结构的振动控制研究［D］.上海:同济大学，2012.

［2］ 王翎羽，陈星等.矩形TLD 减振作用的定量分析方法［J］.建筑结构学报，1995，16(3):29－36.

［3］ GB 50011－2010，建筑抗震设计规范［S］.北京:中国建筑工业出版社.

［4］ 王新敏.ANSYS 工程结构数值分析［M］.北京:人民交通出版社，2007.

［5］ Clough R W，Penzien J.Dynamics of Structures［M］.New York:Mc Graw－Hill，1993.