基于免疫算法的无线传感网络覆盖研究*

马敬思，史旭华，何婷婷，李潇

（宁波大学信息科学与工程学院，浙江 宁波 315211）

1 引言

微机电系统、片上系统、无线通信和低功耗嵌入式技术的飞速发展，孕育出无线传感器网络（WSN，Wireless Sensor Networks），并以其低功耗、低成本、分布式和自组织的特点带来了信息感知的一场变革。由于传感器节点能量有限，覆盖范围和形状不稳定，在进行高密度部署时容易造成传感器节点分布不均匀，节点严重冗余，因此如何对网络覆盖进行优化，以较少传感器节点获得较高网络覆盖率，成为当前WSN研究中的关键课题。

针对WSN覆盖优化问题，大量学者对其进行研究并取得较多的成果，但大部分的成果都是基于0-1感知模型和概率模型。0-1感知模型是一种离散的理想模型，适用于理论研究和数学证明。概率感知模型是一种连续模型，探测概率为目标到传感器的欧氏距离成指数关系。当用网格数学模型建模时，这种概率感知模型在计算时会产生大量数据，对实验结果并没有明显提升。文献[1]中使用了混合感知模型，在覆盖率一样的情况下比0-1模型使用更少的传感器节点，虽然在一定程度上减少了冗余覆盖，但是采取的算法属于单目标优化，不能同时使覆盖率和节点利用率达到最优。

本文采用混合感知模型，能较为实际地反映真实网络。网格化建模后能较大地简化概率计算数据，且能很好地处理联合侦测概率的计算，同时采用基于浓度的克隆选择多目标优化算法（CCSMOA），完成对可行解区域的全面搜索。另外，还区别个体的性能，在进化过程中加大优良个体的克隆倍数的同时也不放弃较差个体，以此来保证算法的优良性能，使区域覆盖率和节点利用率同时达到最优。

2 无线传感器的基本模型

2.1 0-1感知模型

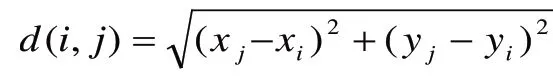
根据上述描述，可以建立数学模型如下：

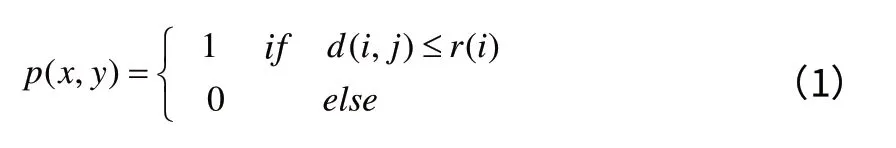
2.2 概率感知模型

随着传感器与监控目标间距离的增大，传感器对目标的感知概率也逐渐减小直至无法感知，称为“概率感知模型”[3]。概率模型的探测概率函数可以表示为：

由式（2）可得，概率模型是一个感知概率随着目标节点j 与传感器节点欧氏距离d(i,j)增大而成指数衰减的模型，λ是传感器节点的衰减系数，只有当d(i,j)为0时，p(x,y)才等于1。

2.3 混合感知模型

由于感知概率在靠近模型处一定范围内接近于1，在距离节点较远处接近为0，这种模型兼具0-1模型和概率模型的特点，所以也称作混合感知模型[1]。

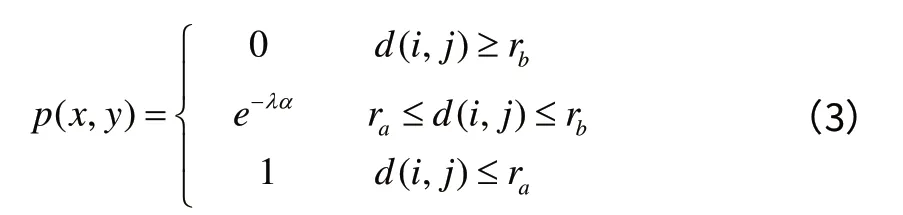
其中，λ是衰减系数，参数α=d(i,j)-rα。

2.4 节点的联合感知

在随机部署中，一个目标可能被2个或以上的传感器节点覆盖，这个目标的叠加的覆盖概率为：

其中，n 为传感器节点个数，Pri为传感器i 的覆盖概率。如果监测目标与两个传感器节点的任何一个的距离越近，则累积覆盖概率也会增加[4]。

3 网格化平台及编码方案

设检测区域为一个二维矩形区域，覆盖区域的面积为A，将传感器节点有计划地投放到监测区域中。本文首先对所投放的N 个传感器节点的工作状态进行二进制编码：S=(s1,s2,…,sN)，则：

如图1 所示，设定投放的节点有2 0 个，将它们进行二进制编码，分成多组：10101 01010 10101 01010。

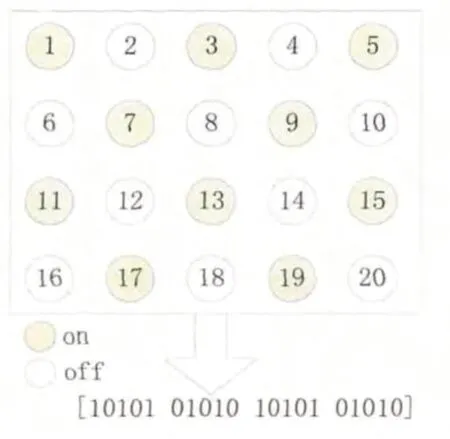
图1 二进制编码

将长为m、宽为n 的矩形监测区域离散化成m×n 个网格，每个网格的面积均为1。任何网格被一个传感器节点覆盖到就认为是被该传感器节点探测到，并且假设此网格被任意节点覆盖是独立的，任意节点之间对目标的覆盖互不干扰。总的覆盖率R 可以表示为：

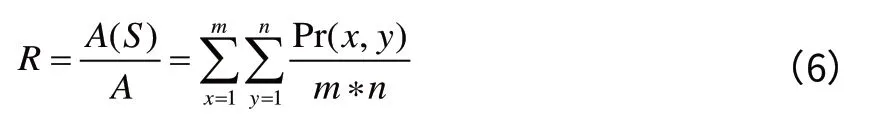
其中，A 是面积为m×n 的检测区域，A(S)是传感器节点集合S=(s1,s2,…,sN)所监测到的目标区域面积，Pr(x,y)是处于第x 行、第y 列的网格点被侦测到的概率。则节点利用率的公式为：

其中，n 为点亮的传感器节点数，N 为总的节点数。

对于0-1感知模型来说，网格点只要被任何一个或者多个传感器节点覆盖到，无论网格点被节点覆盖的面积大小，就认为此网格点100%被感知到了，而混合感知模型则不同。如图2所示，将矩形区域离散化，小圆区域内无论网格点被覆盖的面积大小，被感知概率为100%，如网格点（4,4）；大圆区域以外的感知概率为0，如网格点（1,10）。大小圆之间的环形区域的网格点被感知概率随着目标距离传感器节点越远而变得越小，具体见式（4）。

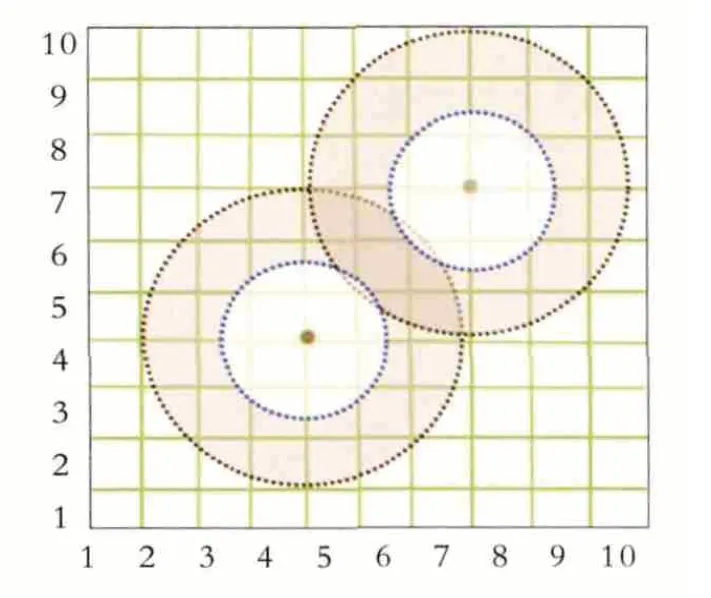
图2 混合感知模型的网格化

4 人工免疫多目标算法

4.1 人工免疫算法

使用免疫算法解决多目标优化问题，从高度抽象的角度来看，在逻辑上生物免疫系统与免疫多目标优化的映射关系如表1所示：

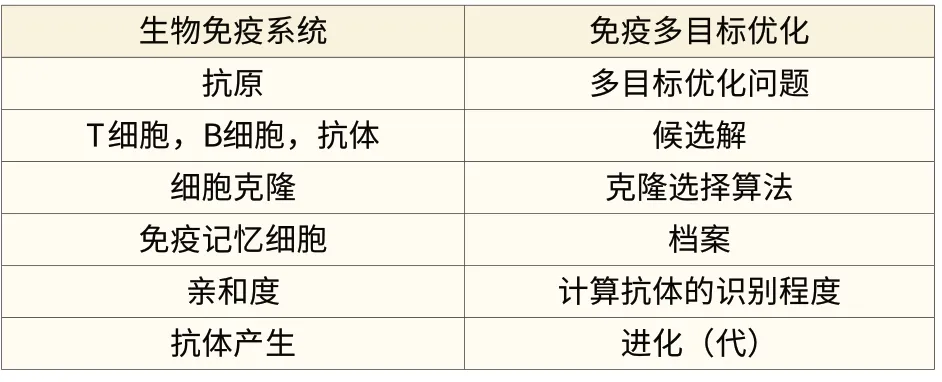
表1 生物免疫系统与免疫多目标优化的映射关系

抗体总是试图以最佳的形态识别抗原，类似于线性规划中求解最优解，所以抗原可以被视为多目标优化的问题[1]。在这里抗原对应覆盖率和节点利用率；抗体被看作是多目标优化的候选解，对应为传感器节点的二进制编码；抗体鉴别抗原的程度可以被视为抗体的亲和度，对应的问题可以描述为：在点亮不同数目以及不同位置的传感器节点情况下，覆盖率和节点利用率的函数关系。

4.2 CCSMOA算法

本文采用基于浓度的克隆选择多目标优化算法（CCSMOA）。该算法的关键在于将每代抗体的克隆次数与抗体浓度更新关联，同时兼顾抗体-抗原亲和力和抗体-抗体亲和力的影响，使抗体浓度的计算转化为一个关于抗体-抗原亲和力和抗体-抗体亲和力的函数，在进化过程中加大对较好解的克隆倍数的同时也不放弃较差解，以此来保证算法的优良性能。

CCSMOA算法流程图如图3所示，其中Pa为初始抗体浓度为C的抗体群。

（1）抗体-抗原亲和力和抗体-抗体亲和力的计算

抗体-抗原亲和力的计算参考了SPEA2算法，因此使CCSMOA算法所求得的解更接近真实的Pareto前沿，也更均匀地分布在Pareto前沿上[5-6]。公式如下：

其中，fiAg表示抗体i 的抗体-抗原亲和力，fSPEA2(i)代表抗体i 在SPEA2算法中的抗体-抗原亲和力。对于抗体-抗原亲和力小于1的非支配解，这时fiAg的值越小表示该抗体和抗原的匹配程度越高，而且密度也小，此抗体越优秀。

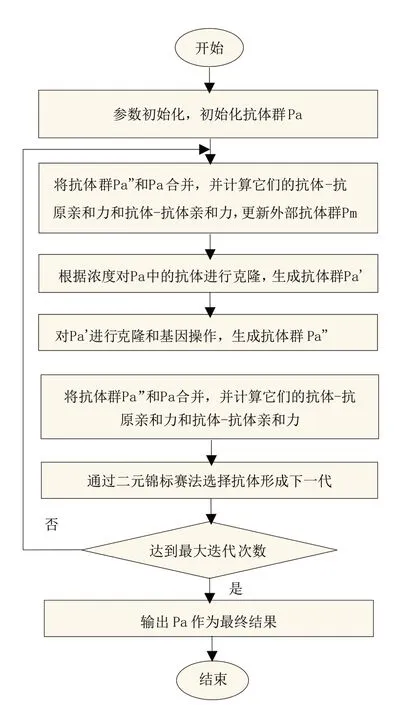
图3 CCSMOA算法流程图

抗体-抗体亲和力主要是为了评估抗体之间的相似性，CCSMOA算法中计算抗体i 与其欧氏距离小于或等于阈值σs的抗体间的相似程度的函数为fiAb(t)，其计算公式如下：

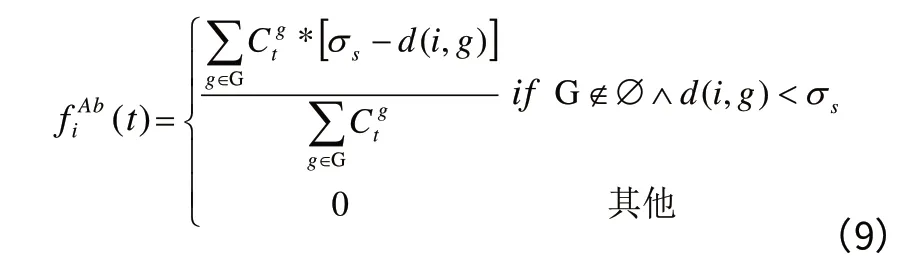
其中，fiAb(t)表示抗体i 在t 代时的抗体-抗体亲和力，G是欧氏距离小于或等于σs的抗体集合，表示抗体g 在t 代时的浓度，d(i,g)表示抗体i 和抗体g 之间的欧氏距离[6]。从式（9）可以看出，只有存在比抗体i 优秀的抗体，抗体i 的抗体-抗体亲和力才不为0，并且只将与其距离在σs范围内的抗体纳入抗体-抗体亲和力的计算，有效保留了在进化过程中相对较差的解，也不至于使得较好的解很快地占据进化过程。

（2）抗体浓度的更新

该算法中抗体浓度的更新取决于抗体-抗原亲和力和抗体-抗体亲和力。抗体的浓度同时又影响了抗体的克隆次数，基于以上把抗体浓度的更新定义为上一代的抗体浓度和抗体-抗原亲和力的函数，计算公式如下：

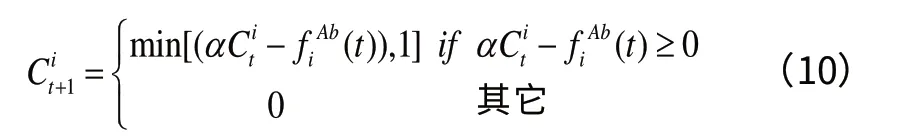
其中，Cit1和Cit的范围都是[0,1]，且分别代表抗体i 的新旧浓度。比例系数α 决定了抗体浓度所占的比重，这个比重又取决于抗体的抗体-抗原亲和力，其计算公式如下：

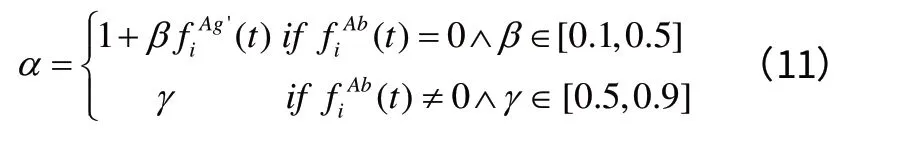
（3）克隆基因操作和外部记忆抗体群更新

在每次迭代中，每个抗体都有自己的克隆倍数，此算法中每个抗体的克隆倍数取决于自身的抗体浓度。那么，浓度为 Cit抗体i 的克隆倍数为：

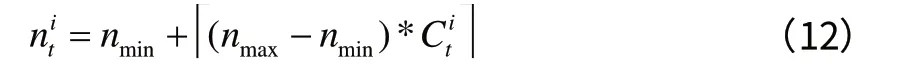
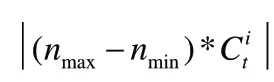
随后对克隆后的抗体群实施交叉和变异操作。交叉操作采用模拟二进制交叉，它的数学描述为：

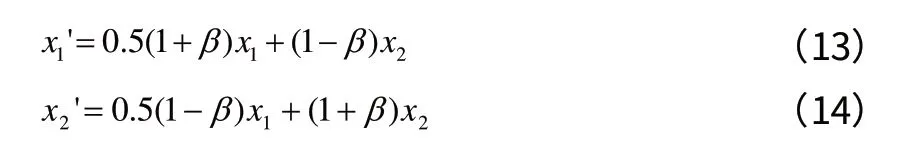
式（13）、式（14）分别表示抗体 x1和抗体 x2经过交叉得到的抗体 x1'和抗体 x2'的计算公式。其中β的数学描述为：

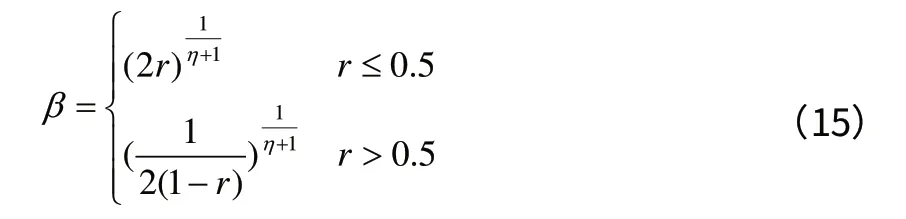
其中，r 是[0,1]的随机数，η 为分布指数。η 越大，则通过交叉操作产生的子代抗体就与父代抗体越相近；反之，则会越远[9]。

变异操作采用由Deb提出的多项式变异[10]。多项式变异是目前多目标优化算法中常用的一种变异方法，它的数学描述是：

其中β 的数学描述为：

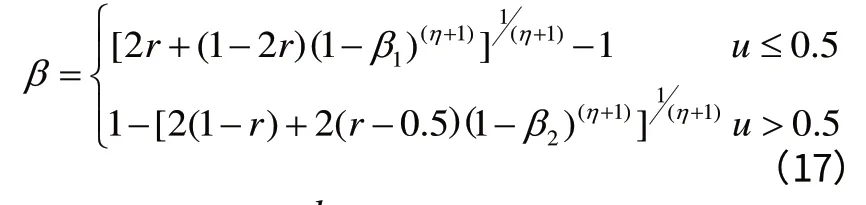
5 仿真及结果分析

设定检测区域为200m*200m的矩形区域，混合感知模型的ra为10m、rb为15m，衰减系数λ 为0.01，分别部署1 5 0 个节点到此区域，CCSMOA 算法和NINA算法的参数指标：变异概率β 为0.1，抑制阈值σs为0.06，算法迭代次数为100。则得到的仿真图如图4所示：

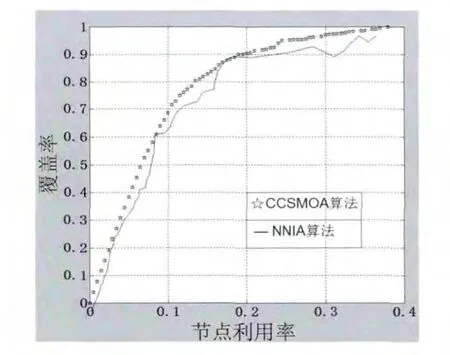
图4 2种算法的混合感知模型仿真图

由图4可以看出，CCSMOA算法的曲线比NINA算法的平滑，而且覆盖率超过0.8曲线部分，CCSMOA算法的点数明显比NINA算法的密集，这是由于NINA加强了对所谓精英区域的搜索，而放弃对那些可能存在好的解的区域的搜索，从而导致过早地局部收敛，很难达到全局最优。而CCSMOA算法能对可行解区域全面搜索，同时也要区别好的和坏的个体，在进化的过程中加大对较好解的克隆倍数的同时也不放弃较差解，以此来保证算法的优良性能，使区域覆盖率和节点利用率同时达到最优。

设定检测区域为100m*100m的正方形区域，0-1感知模型的r(i)为12m，得到的仿真图如图5所示：

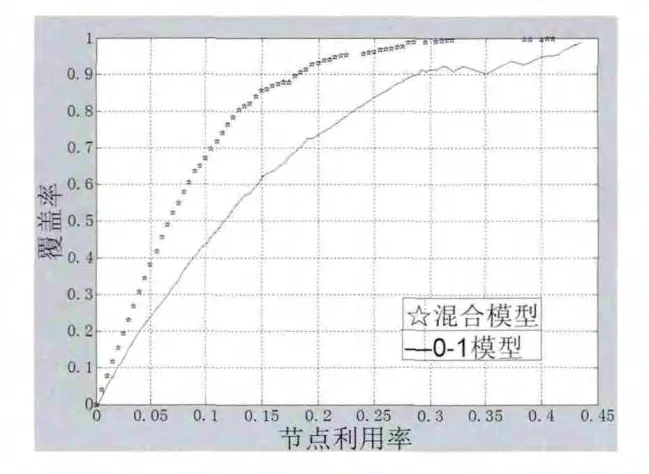
图5 0-1感知模型和混合感知模型100m*100m区域覆盖

从图5可知：当节点利用率为0.1时，0-1感知模型覆盖率为45%，而混合感知模型能达到将近70%；当利用率为0.2时，混合感知模型已经达到90%，而0-1感知模型不到75%。

如图6所示，将覆盖区域改为200m*200m，投放的节点数目改为300，其他参数不变。CCSMOA算法在覆盖率和节点利用率上的优化并没有什么改进，但是100m*100m区域覆盖在节点利用率从0.3到0.4之间出现了缺失或者曲线波动较大，这个情况在200m*200m的区域覆盖时并没有出现。这是由于100m*100m的解空间较小，算法的收敛出现问题，没有找到最优解。虽然混合感知模型的曲线由于CCSMOA算法的收敛性还不够优秀而呈现出些许曲折，但是在覆盖率和节点利用率这2个目标的优化上，混合感知模型比0-1感知模型在仿真中表现得更优异。

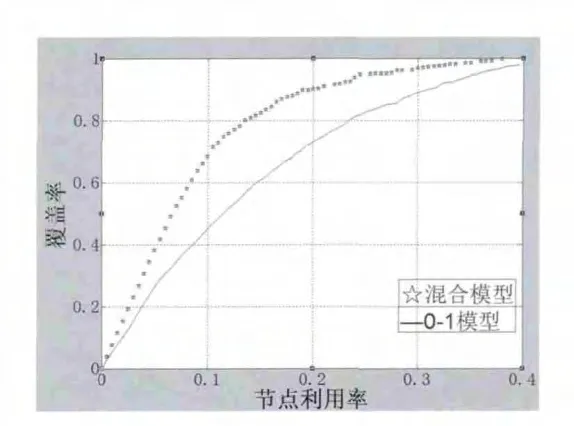
图6 0-1感知模型和混合感知模型200m*200m区域覆盖

6 结束语

本文将基于浓度的克隆选择多目标优化算法（CCSMOA）用于无线传感网络的网格化平台，通过对抗体浓度的控制，完成对可行解区域的全面搜索，同时也要区别不同的个体，在进化的过程中加大对较好解的克隆倍数的同时也不放弃较差解，以此来保证算法的优良性能。仿真结果表明，CCSMOA算法能使区域覆盖率和节点利用率达到较好的平衡。

[1] 王震,陈云芳. 基于人工免疫的多目标优化研究综述[J]. 计算机应用研究, 2009(7): 2422-2426.

[2] Chakrabarty K, Iyengar S S, Qi H, et al. Grid Coverage for Sutveillance and Target Location in Distributed Sensor Networks[J]. IEEE Transactions on Computers, 2002,51(12): 1448-1453.

[3] Dhillon S S, Chakrabarty K, Iyengar S S. Sensor Placement for Effective Coverage and Surveillan in Distributed Sensor Networks[A]. IEEE Wireless Communication and Networking Record[C]. Piscataway: IEEE, 2003: 1609-1614.

[4] Cao Qing, Yan Ting. Analysis of Target Detection Performance for Wireless Sensor Networks[A]. International Conference on Distributed Computing in Sensor Systems[C]. 2005: 276-292.

[5] 雷德明,严新平. 多目标智能优化算法及其应用[M]. 北京: 科学出版社, 2009.

[6] 刘楠楠,史旭华. 基于抗体浓度的克隆选择多目标优化算法及其应用[J]. 宁波大学学报: 理工版, 2013(3): 57-61.

[7] 焦李成,尚荣华. 多目标优化免疫算法、理论和应用[M]. 北京: 科学出版社, 2010.

[8] 曾广朴,仲元昌,范会联. 混合无线传感网络覆盖优化的粒子群算法[J]. 微电子学与计算机, 2011(8): 105-107.

[9] 崔逊学. 多目标进化算法及其应用[M]. 北京: 国防工业出版社, 2006.

[10] 焦李成,杜海峰. 人工免疫进展与展望[J]. 电子学报, 2003(10): 1540-1548.

[11] 程博,郭振宇,王军平,等. 一种并行免疫进化策略算法研究[J]. 控制与决策, 2007(12): 1395-1398.★