羽绒蓬松度测定结果不确定度的评定
赵金晶 董爱林 陈惠敏
(江苏省纺织产品质量监督检验研究院,江苏南京 210007)
测量不确定度表征合理地赋予被测量之值的分散性,是与测量结果相联系的参数[1]。在ISO /IEC 17025《检测和校准实验室能力认可准则》[2]中规定,测试报告需有评估测量不确定度的声明(适用时),如果不确定度与测试结果的有效性或应用有关,或客户说明中提出要求,或不确定度影响与规范限量的符合性时,测试报告中需加入有关不确定度的信息。测试结果包含不确定度信息后,可使测试结果的表达更科学、完整。另外,测量不确定度在实验室数据比对、方法确认、标准设备校准、量值溯源以及实验室质量控制和管理等方面具有重要的意义。
冬季常见防寒保暖的羽绒服,消费者最关注的是保暖功能。蓬松度是指羽毛羽绒的弹性程度[3],羽绒蓬松度越好,滞留的空气量越多,保暖性越好。因此,蓬松度是羽绒产品重要的检验项目,国家标准对其也做了相应规定,国内对于羽绒蓬松性能相关因素之间关系的研究也正逐步展开。本文通过对羽绒蓬松度测量不确定度的来源进行分析探讨,定量表征测量结果的质量,确定羽绒蓬松度测定结果的可信程度。
本文主要按照GB/T 14272-2011开展试验并进行不确定度评定,同时FZ/T 80001-2002、GB/T 10288-2003等标准[4,5]亦规定了完全相同或相似的羽绒蓬松度的检测方法,本文的分析方法和结果具备一定的普适性。
1 试验
1.1 试验方法及原理
依据GB/T 14272-2011《羽绒服装》附录C中蓬松度的测定方法,其原理是通过测量在一定口径的容器内一定量的羽绒羽毛在恒重的压力下所占的体积来计算蓬松度。
1.2 试验样品
实验选取含绒量标称为 80% (x%为样品的含绒量)的灰鸭绒作为实验样品。
1.3 试验条件及仪器
样品在恒温箱(50℃±5℃)内恒温处理1h后,用手逐把抖入前处理箱内,在温度20℃±2℃及相对湿度65% ±4%的标准大气中静置24h使其疏松,恢复原状备用。
仪器设备有天平、秒表、前处理箱、蓬松度仪(桶壁两对面有刻度的有机玻璃圆筒,桶高75cm,内径为24cm,桶底为有机玻璃活络底。桶内有直径为24cm,质量为68.4g的可以在桶内上下自由滑动的圆形铝质压板)、恒温箱。
1.4 试验步骤
1.4.1 从在前处理箱内已放置24h的羽毛、羽绒样品中,称取两个28.5g试样,逐把抖入蓬松仪内,再用硬质玻璃棒充分搅拌并铺平。
1.4.2 铺平后,将铝质压板盖在羽毛、羽绒上面,在松手放下压板的同时按下秒表,任压板缓缓下压。1 min 后记录压板压在蓬松仪桶壁的两边刻度值,取其平均值。同一试样重复做三次。
1.4.3 结果计算。按式(1)计算三次试验结果的平均值,作为试样蓬松度的测定值。计算结果按GB/T 8170[6]修约至小数点后一位。

(1)式中:h1为第一次试验结果的刻度平均值(cm);h2为第二次试验结果的刻度平均值(cm);h3为第三次试验结果的刻度平均值(cm)。最终结果取两个试样的平均值,计算结果按GB/T 8170修约至小数点后一位。
2 不确定度来源分析和评定
根据羽绒蓬松度测定的程序步骤,分析羽绒蓬松度不确定度的来源的因素,具体关系如图1所示:
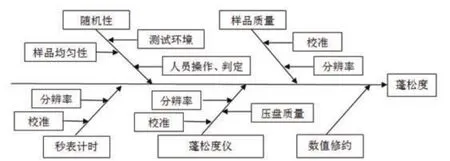
图1 蓬松度测定不确定来源图
2.1 随机效应导致的不确定度
从测试方法可以看出,羽绒蓬松度的测量主要靠人工操作,因此测量不确定度将部分来自于试样取样、前处理和实验进行过程中环境因素(温度、湿度等)的随机性和实验人员操作、判定的随机性。
按照1.4所述方法,我们将一组相同样品在不同的实验时间,由不同的实验人员分别进行取样、前处理和实验测定,得到蓬松度测量数据见表1。

表1 样品蓬松度测量结果及偏差计算
单次测量的不确定度(试验标准偏差)由以下贝塞尔公式计算:

(2)式中Xi为第i次蓬松度的测定值,X为n次测量蓬松度的平均值,n为测量总次数,S(x)为单次测量的不确定度。
采用肖维勒准则剔除异常值,对于测量次数为10次时,异常界限系数k=1.96,则

据此检查表1中10组测量数据,均为有效测量值。
在日常分析中,测定两份样品报告平均值,故平均值的标准偏差为:

此标准偏差相对于15.2cm的蓬松度而言,测量的随机效应产生的相对不确定度为
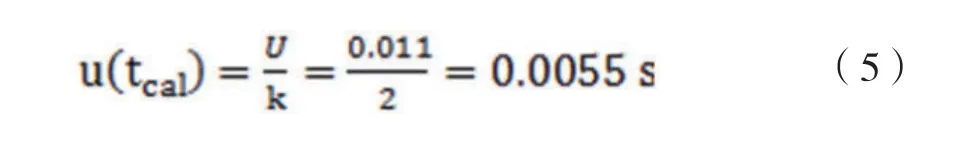
2.2 样品质量测量引入的不确定度
a. 天平称量的校准
实验室所用天平为梅特勒-托利多PL2002型电子天平。由检定证书可知.天平偏载误差±0.02g,重复性误差±0.01g,示值误差±0.02g (0≤m≤500g)、±0.02g(500<m≤2000g)、±0.02g (2000<m≤2100g),样品质量约为28.5g,假定分布均匀(矩形分布),则由天平校准引起的不确定度分量可表示为:

b. 天平称量的读数精度(分辨率)
试验实际使用的天平分度值为0.1g,假设为矩形分布的半宽,则由天平称量读数引起的不确定度分量可表示为:
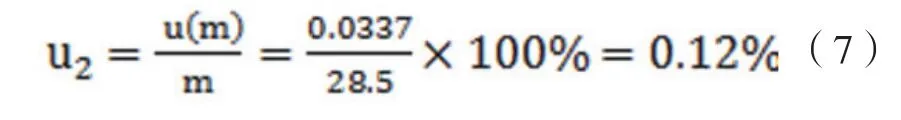
上述2种分量合成得到样品质量测量的标准不确定度为:
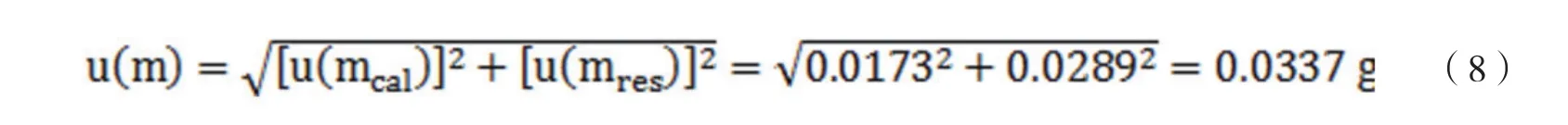
对于28.5g样品而言,样品质量测量的相对不确定度为:
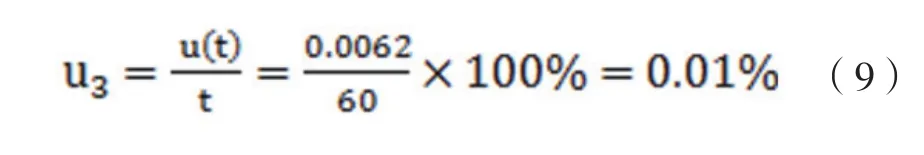
2.3 时间测量引入的不确定度
a. 秒表计时的校准
用于计时的秒表,根据检定证书标明其在测量范围1~120s条件下,扩展不确定度U=0.011s,k=2,则其标准不确定度为:
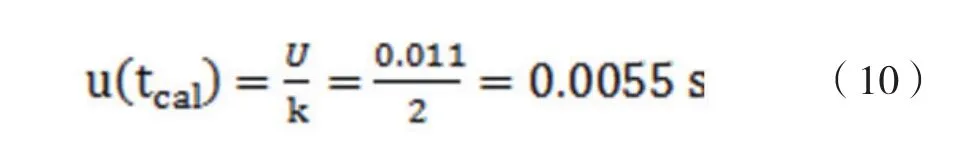
b. 秒表计时的读数精度(分辨率)
使用的秒表分度值为0.01s,假设为矩形分布的半宽,则有
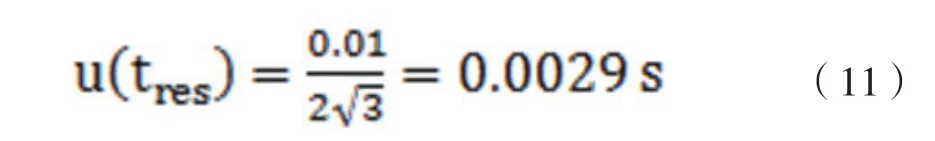
上述2种分量合成得到时间测量的标准不确定度为:

对于60s样品实验时间而言,时间测量的相对不确定度为:
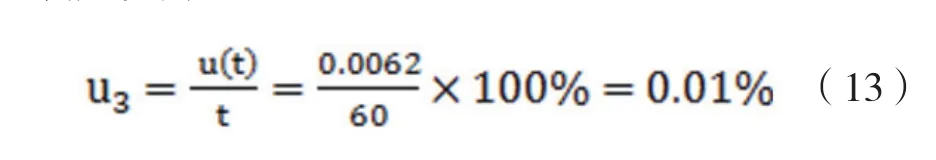
2.4 蓬松度仪引入的不确定度
本实验所用蓬松度仪存在两方面主要的不确定因素,一是蓬松度仪体积测量,二是蓬松度仪所用压盘质量。
2.4.1 蓬松度仪体积测量
a. 蓬松度仪体积的校准
根据计量证书提供的结果,在符合要求的实验环境下,实验所用仪器容积为16000±104.2cm3(计量中已考虑容器底面积的变化,故后续不再重复计算底面积变化引起的不确定度),但并未给出置信水平或分布情况信息,为此假设符合三角形分布,则有:
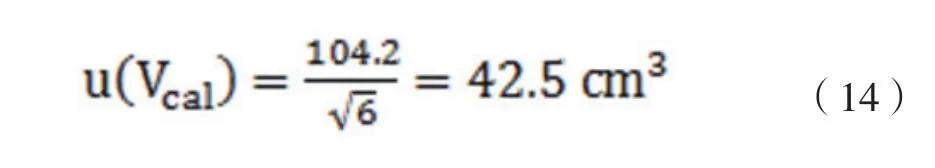
b. 蓬松度仪的读数精度(分辨率)
实验所用仪器分度值为 200cm3,假设为矩形分布的半宽,则有:

上述2种分量合成得到体积的标准不确定度为:
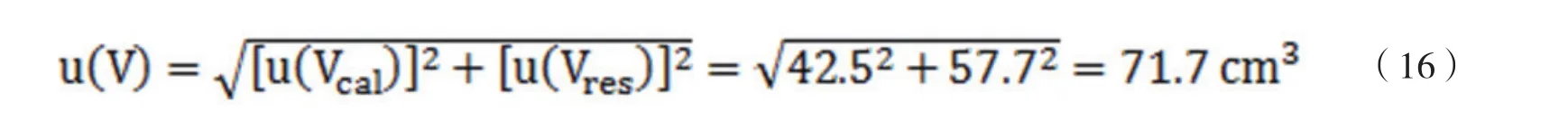
相对于15.2cm的蓬松度(对应体积V=15.2*3.14*122=6872.8 cm3),蓬松度仪测量的相对合成不确定度为:
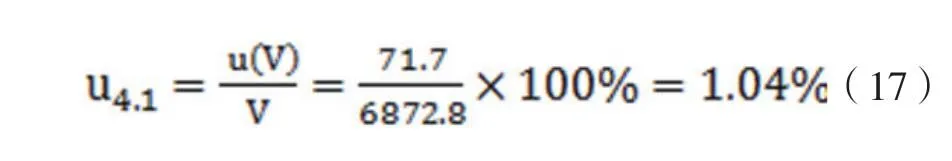
2.4.2 蓬松度仪压盘质量
根据仪器计量证书提供的结果,压盘质量为68.4±0.3g,假设为矩形分布,压盘质量相对不确定度为:

2.5 数值修约引入的不确定度
按照GB/T 14272-2011试验方法的规定,计算结果修约到0.1cm。根据JJF1059-1999[7]规定,计算平均值修约导致的不确定度:
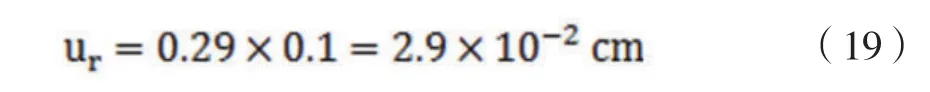
相对于15.2cm的蓬松度,修约导致的相对不确定度为:

2.6 合成不确定度
有上述分析可知,相对合成不确定度的计算为:

合成标准不确定度为:
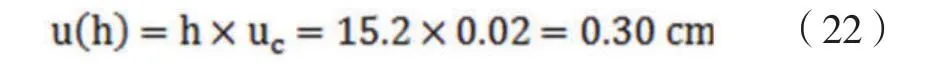
2.7 扩展不确定度
取包含因子k = 2 ( 近似95%置信概率) ,则扩展不确定度为:
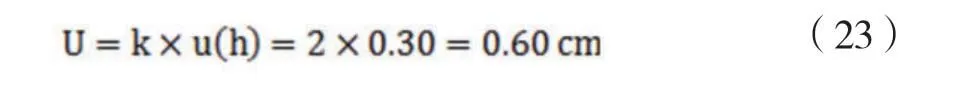
2.8 不确定度报告与表示
综上,实验羽绒蓬松度的结果可表示为: k = 2。
3 结论
分析显示,在本文所采用的试验方法和测量条件下,各不确定度分量对羽绒的蓬松度的影响不同。总体来说,测量的随机效应u1和蓬松度仪的精准程度u4对不确定度总量影响最大。其中,随机效应导致的不确定度占据了最大的部分,这除了与样品均匀性、测试环境等客观因素有关之外,也与实验人员的操作、判定有直接联系。与此同时,蓬松度仪作为本项实验所用到的最为重要的仪器,它也是很重要的一个不确定度分量,其精密程度很大程度上制约了羽绒蓬松度测量的准确性。
所以在检测过程中要严格按照操作程序,使用精度高、稳定性好的仪器设备,并在试验前认真校准,减少人为因素和判定的不当,遵守数值修约的规定,同时注意应用测量技巧也可有效减少羽绒蓬松度测量中的不确定度。
[1] ISO/lEC Guide 99: 2007 International vocabulary of basic and general terms in metrology (VIM) [s].
[2] ISO/IEC 17025 : 2005.检测和校准实验室能力认可准则[s].
[3] GB/T 14272-2011.羽绒服装[s].
[4] FZ/T 80001-2002.水洗羽毛羽绒试验方法[s].
[5] GB/T 10288-2003.羽绒羽毛检验方法[s].
[6] GB/T8170-2008 数值修约规则与极限数值的表示和判定[s].
[7] JJF 1059-1999. 测量不确定度的评定与表示[s].

