网络考试系统中组卷算法比较及应用

龚 利

(郧阳师范高等专科学校，湖北十堰442000)

在网络考试系统中，组卷模块是核心模块，一份试卷组合是否科学，是否难易适中都由组卷模块来实现，因此，组卷模块算法的优劣将决定该网络考试系统的开发成败。

1 几种算法比较

在网络考试系统中，智能组卷技术通常有以下三种算法:回溯试探法、随机选取法及遗传算法。

1.1 回溯试探法

该算法将随机产生的每一状态类型都记录下来，系统在搜索时，当遇到失败时，就会释放掉上次随机产生记录的状态类型，然后，依据一定的策略，再将其转变成一种新的状态类型进行记录和试探，在通过不断的回溯试探搜索，直到我们的试卷生成完成，或者搜索本次失败。这种算法对于状态类型少，或者组卷题量较小的试题库时，它们生成的试卷组卷成功率是比较高的，但通过实际应用分析可以看到，这种算法有以下几个缺点:程序结构复杂、内存消耗量大、不能随机的选取试题。

1.2 随机选取法

该算法可以根据目标需求的控制指标，从试题库中随机的抽取试题生成到试卷内，经过循环，一直到组卷生成完毕。或者组卷模块无法从系统试题库中，提取到满足控制指标的题目而终止。随机选取法的优点就在于其结构简单，抽取试题速度较快，但对于整个组卷过程来说，组卷成功率低，通常要花费相当长的时间，才能完成试卷的生成。

1.3 遗传算法

这是一种并行的、智能优化的算法，其模拟了达尔文自然进化论中“优胜劣汰、适者生存”的进化法则。其随机的以一定规模在试题库中初始化一个种群，然后算法自动按照约束，在试题库中，寻找符合约束条件的组卷，遗传算法的优点就在于其可以在试题库中有效的搜索满足控制指标的试卷信息，因此，网络考试系统系统选用遗传算法来完成试卷的自动组卷技术。

2 遗传算法在组卷模块中的应用

在组卷模块中，主要从组卷模块的业务处理流程、组卷算法、遗传算法及改进和组卷数学模型四个方面进行介绍。

2.1 组卷模块业务流程

组卷模块的主要业务流程如图1所示。

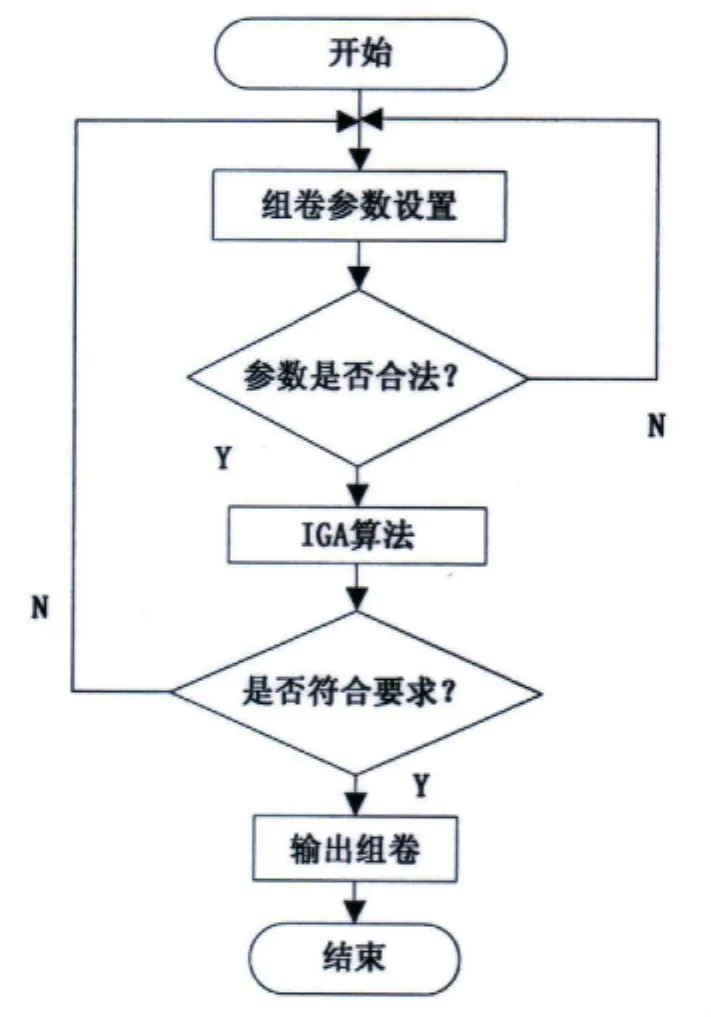
图1 组卷模块业务处理流程

通过图1，我们可以看到组卷模块流程:开始需要对组卷参数进行设置，其遗传算法参数设置有:交叉概率(PC)、种群规模(Popsize)及变异概率(Pm);组卷参数应该有:总分数，题型分数、试卷难易度、考试知识点覆盖度、试卷区分度以及考试起始时间。然后点击生成试卷，系统对用户输入的参数进行合法化检查，不合法提示用户，并让用户重新设置参数，否则，继续下一步，进入遗传算法(IGA)算法处理流程，等待IGA生成组卷，选择符合要求的试卷，并保存，否则返回组卷参数设置界面，重新设置组卷参数［1］。

2.2 组卷算法

组卷算法流程伪代码如下:

(1)Step1:随机初始化种群规模为popsize大小的种群P，并初始化一个大小为「popsize/2」的外部归档集NDSet;

(2)Step2:分析种群中有多少个染色个体，然后对染色个体进行解码，通过对第i个组卷指标值Fi的利用，计算出Fi和个体的指标值它们之间的绝对误差值fi，并根据第i个指标的权重Wi，进行个体适应值评价，计算出种群P中个体的适应度;

(3)Step3:迭代计数器gen=1;

(4)Step4:如果gen=1，则在种群P中，选择适应度较高的前「popsize/2」个体保存至归档集NDSet中，否则在种群P中，选择适应值较高的前「popsize/2」个体后，与当前归档集NDSet中的个体比较，选择适应值高的前「popsize/2」个个体保存至外部归档集NDSet中;

(5)Step5:利用自适应遗传算子使种群P进行遗传操作，并使得种群P的个体规模2*popsize;

(6)Step6:分析种群P中有多少个染色个体，然后对染色个体进行解码，通过对第i个组卷指标值Fi的利用，计算出Fi和个体的指标值它们之间的绝对误差值fi，并根据第i个指标的权重Wi，进行个体适应值评价，计算出种群P中个体的适应度;然后按个体适应度的高低进行排序，选择popsize个个体保存到种群P;

(7)Step7:gen=gen+1;

(8)Step8:若 gen＜ Gen，则跳转至 Step4，否则输出种群P和归档集中，选择出符合要求的生成试卷进行输出。

2.3 遗传算法及改进

遗传算法具有并行性和智能优化算法等特点，它为解决复杂优化问题提供了一个良好的框架，然而由于遗传算法的随机性，导致算法出现波动性或容易陷入停滞现象。因此，对遗传算法做出以下两点的改进。

(1)自适应遗传算法

遗传算法在进行到早期时，在种群中个体之间的差异比较大，有较大的交叉概率和较小的变异概率，这时的遗传操作，它有助于保存种群的遗传基因;然而，随着演化过程的变化，种群中个体之间的差异越来越小，交叉概率和变异概率越小，有利于增加种群个体的多样性，增强了全局搜索能力的途径，克服算法的容易出现早熟现象。所以，系统可以采用自适应交叉变异概率，其算法如式1所示［2］。

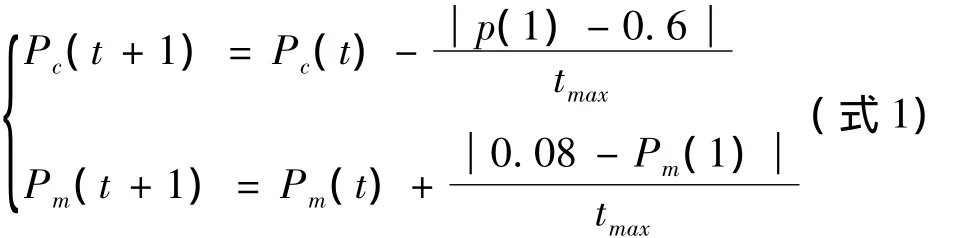
(2)精英保持策略

遗传算法是基于随机演化选择的算法，导致其搜索出来的结果一般具有波动性特点，为减少算法的波动性，使得算法加快收敛，通过对遗传算法改进，加入了精英策略(Elitism)。精英策略算法的实现方式有两种:

第一是对新旧群体进行合并，选择下一代种群的方式，增大了适应度较高个体(精英个体)在后代种群中出现的概率，来实现种群中的精英保持。

第二是在种群之外，设置一个独立的伴随种群(archive)，其作用是保留与更新算法演化过程中搜索到的优良个体，进而实现精英保持。

通过上面的分析，自适应遗传算法及精英保持策略加入遗传算法进行改进。也可称为改进的遗传算法，即IGA算法。

2.4 智能组卷模块数学模型

生成一份科学、规范、合理的试卷是我们组卷的目标，具有一定的性能要求及约束条件，一般来说，组卷应包括:总分数、章节分数、题型分数、试卷难易度、试卷区分程度、考试起始时间等。通过实地调研考察，组卷数学模型需要完成的如下目标:

(1)试卷的总分必须达到规定的分值，如100分;

(2)各个题型的分值比例需要符合规定的比例;

(3)使得同一试题在连续几次的组卷中被选取的频率尽可能的低;

(4)试卷的难度、区分度适当，应该满足所设定的平均分与不及格率。

因此，通过对试卷组卷目标的分析，我们可以确定试题的状态特征，对于网络考试系统中的试题库，它的每道试题通过建立目标状态矩阵 ，如式2所示。

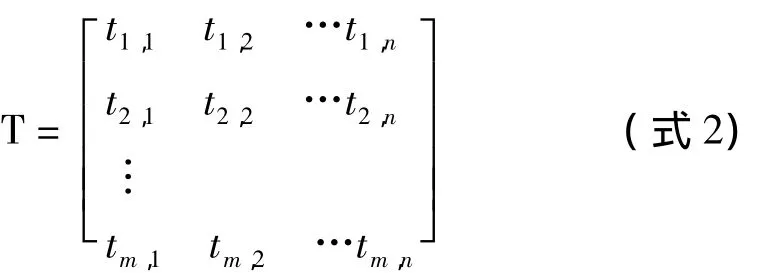
其中，m表示试卷题目的数目，n为试卷是每个题目的属性参数(在系统生成试卷时，组卷对题目的属性参数需求最大值为 n=7)。tij表示第 i题的第j个属性。j=1表示第i题的分值，j=2表示第i题的章节编号，j=3表示第i题的题型，j=4表示第i题的难度，j=5表示第i题的答题时间，j=6表示第i题的知识点编号，j=7表示第i题的试卷区分度。

在矩阵中，每一行表示一个测试题目和其属性，每一列代表所有测试的题目的相关属性。组卷流程解决问题:根据用户输入或默认生成试卷的要求，找到矩阵中满足生成试卷的行组合，其结果是在矩阵T中，搜索确定出全部行状态的多变量(K1，K2，…，Km)。变量Kt是矩阵中第i行的状态变量(即试题库中第 道测试题目)，若Ki=0，则说明第i行没有选中，若Ki=1，则说明第i行选中。

在实际应用中，为了克服算法的盲目性和随机性，我们需要构造出相应的适应值评价函数(式3所示)，就可求解一般约束优化问题。

通过适应值评价函数可以看到，为了使得整个试卷指标f最小化，fi参数为:第i个指标和用户需求之间的的误差绝对值，ωi参数为:第i个指标所对应的权重。而测试题目的权重ωi的参数确定是根据测试题目第i个参数的确定的，这个由用户来输入，可以得到权重之和，即第 i个权重0≤ωi≤1。因此，改进的遗传算法IGA的适应值评价函数为式3所示。

3 结束语

遗传算法在组卷过程中，其在优化搜索方法方面和整体搜索策略方面，可以不用依靠其它辅助信息，只要构造出相应的适应值评价函数，就可以求解出一般约束优化问题，并在组卷过程中较好地克服算法随机性及盲目性等缺点。另外，遗传算法能够应对网络考试系统随时更新的试题题库以及相关组卷要求，所以在网络考试系统中，组卷模块选择遗传算法是能够实现科学公正组卷的目的。

［1］蒋国瑞.开放式远程教育智能考试管理系统［J］.计算机工程，2004，30(21):190-192.

［2］张兴军，钱德沛，张然.一种实现Web应用服务器安全的新方法［J］.计算机工程与应用，2001(19):16-17.