自励式液冷电磁缓速器的数值模拟与实验研究*

张 凯,李德胜,尹汪雷,郑 然

(北京工业大学机械工程与应用电子技术学院，北京 100124)



2015123

自励式液冷电磁缓速器的数值模拟与实验研究*

张 凯,李德胜,尹汪雷,郑 然

(北京工业大学机械工程与应用电子技术学院，北京 100124)

为克服传统电涡流缓速器持续制动时制动转矩热衰退严重的问题和节约能源，提出一种新型自励式电磁液冷缓速器结构。运用有限元法分别对该缓速器电磁场和制动性能进行分析，应用有限体积法对缓速器瞬态流场-热场进行数值模拟。通过台架试验对缓速器特性进行测试，结果表明，仿真结果与实测数据吻合较好，制动转矩可达1 600N·m，且在持续工作时制动转矩热衰退在5%以下，满足车辆需求。

电磁缓速器；液冷；自励式；数值模拟；实验研究

前言

目前电涡流缓速器已经成为一些重型车辆和客车的标准配置[1]。自励式双凸极电涡流液冷缓速器在节约能源和制动性能方面比其他的辅助制动装置更有优势[2]。

日本泽藤电机株式会社[3-4]设计了一种自励式电涡流缓速器，风冷结构，制动转矩不超过1 000N·m。文献[5]中提出一种双转子盘式自励式电涡流缓速器，可以实现自励，但其质量和体积大，制动转矩衰退达到40%，不能胜任山区道路运营的要求。

在理论研究方面，国内外学者运用有限元法对缓速器模型进行三维稳态涡流分析和瞬态温度场与应力场分析，取得了很好的效果。文献[6]中采用A、φ-A法和库伦规范建立和求解了列车制动时涡流分布模型，即把涡流场分为涡流区和非涡流区，分别对两个区域进行分析。文献[7]和文献[8]中运用基于移动坐标系的有限元法对缓速器三维瞬态涡流场进行分析，并对缓速器结构参数进行优化。文献[9]和文献[10]中应用有限元法对轨道辅助制动系统做了深入研究，获得了很好的计算效果。文献[11]中对缓速器转子的疲劳寿命进行预测，应用有限元法对瞬态温度场和应力场进行了分析，并讨论了转子钢蠕变疲劳性能。文献[12]中利用试验数据拟合得到了缓速器制动转矩-速度-电流之间的关系式，并利用该关系式对缓速器制动力矩进行控制。文献[13]中利用电磁场有限元法对缓速器制动性能进行了参数化分析，对以后缓速器制动特性分析有一定的指导意义。有些学者在内表面涡流区镀金属层来分析涡流深度对制动特性影响。文献[14]中在分析铜质和铁质圆柱的制动特性时考虑了集肤效应影响。文献[15]中采用傅里叶变换法和有限元法对3mm厚旋转铝盘在磁场作用下的制动特性进行分析。文献[16]中运用有限元法进行瞬态电磁场分析，运用磁热耦合方法对瞬态温度场进行分析，得出永磁水冷缓速器涡流场与温度场的分布规律，取得了良好的制动性能。在磁场分析中大多数学者均忽略漏磁和不考虑磁路的磁滞损耗和杂散损耗的影响,忽略涡流场中位移电流和磁场的空间高次谐波。

为克服传统电涡流缓速器热衰退严重的问题和节约能源，本文中提出一种新型自励式电磁液冷缓速器结构，采用无电刷结构和液冷散热方式，该结构简单实用、可靠性好，解决了自励缓速器持续工作时制动转矩热衰退严重的问题，同时在持续制动时对汽车电源不造成冲击，并且通过大量测试缓速器的制动特性和自然特性。

1 结构与工作原理

新型自励式电磁液冷缓速器由内置水道的定子、线圈和转子组成，其结构如图1所示。线圈绕组固定在定子内侧，转子是H型齿状转盘，与主轴相连。永久磁铁嵌在转子内侧作为发电系统的转子。当缓速器工作时，主轴拖动转子旋转，发电机发出的电通过控制系统给缓速器线圈供电，提供励磁电流。根据电磁感应理论，缓速器转子、定子之间的相对运动使气隙磁通密度发生周期性变化，在每个凸极处对应的定子内表面切割磁力线，产生交变磁场，并在定子内侧感生涡流电势，从而产生制动转矩。涡流产生的热由定子内部的循环水带走。

图2为缓速器的磁路分布图。其中，图2(a)为缓速器工作状态时的磁路分布，由图可见，制动系统的磁路为轴向，而发电系统的磁路为周向，二者相互垂直，互不影响。图2(b)为缓速器非工作状态时的磁路分布，此时只有永久磁铁产生的磁场，在进行有限元分析时缓速器无制动转矩产生，说明发电机磁场对缓速器磁场不产生影响，样机试验也验证了该磁路的合理性。

2 数值分析

通过对缓速器模型制动系统的磁场、温度场、制动特性和发电系统的发电量进行分析，给出整个系统的理论分析结果。图3为缓速器的1/12分析模型。转子的凸极数为12，永久磁铁为12块，定子材料为低碳钢，转子材料为电工纯铁。仿真所使用的材料特性是当温度为100℃时所标定的特性。

2.1 制动系统

为了便于制动系统的分析，做出以下假设：(1)忽略曲率及涡流场中位移电流；(2)忽略磁路中的磁滞损耗和杂散损耗；(3)忽略由温度引起的材料特性的变化。

图4为制动系统分析模型。在瞬态分析中，线圈中励磁电流设为10～40A，转子转速为250～1 500r/min，简化的磁路图如图5所示。缓速器模型的主要几何参数见表1。

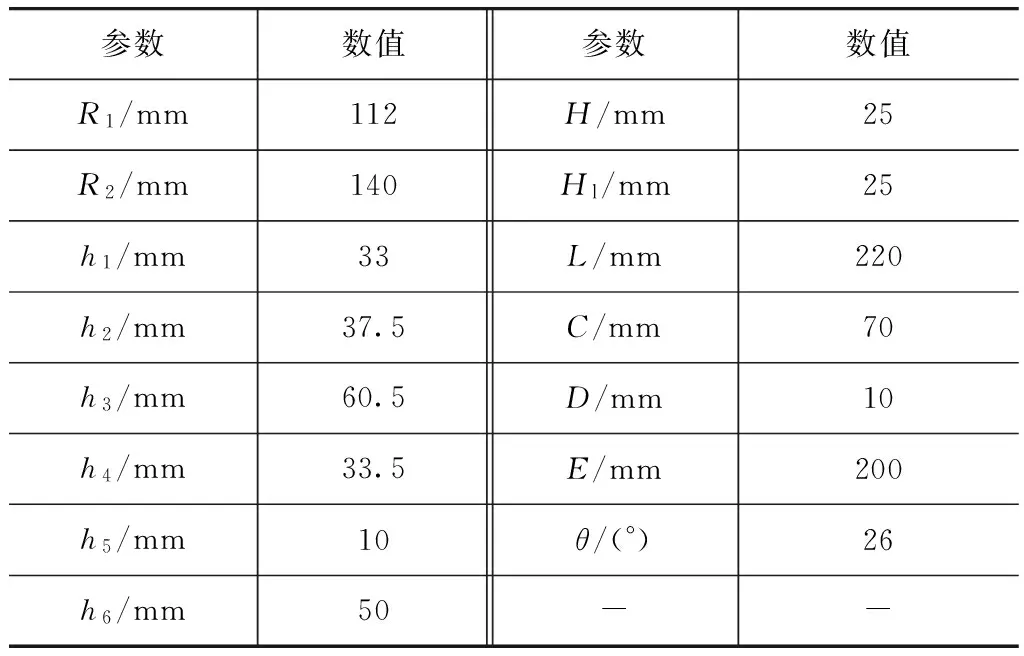
表1 缓速器主要参数表

经过简化后磁路的总磁阻ΣR为

∑R=2(Rab+Rbc+Rcd+Rde+Rfa)

(1)

产生的磁场强度B为

(2)

式中：B为磁场强度；F为磁动势；S为截面面积。

根据电磁感应定律，y处的感应电场强度为

Ez=ωBy

(3)

电流密度Jz为

Jz=σEz=ωσB0y

(4)

由此可知，定子内表面的电流密度与角频率ω=2π/f和B有关。

由于集肤效应，涡流主要集中产生在定子内表面，集肤深度δ为

(5)

式中：μ为磁导率；σ为电导率；ω为磁场变化的角频率。

气隙中磁场分布和磁场强度决定了制动转矩的大小[17]，气隙磁场的强度与转子转速、截面面积以及励磁电流有关，采用有限元法分析气隙磁场分布。图6是缓速器制动系统模型的磁场分布,励磁电流为26A，转速为1 500r/min。分析结果说明，凸极处和定子截面(cd处)易出现饱和，设计时应避免此处在未达到设计要求前发生饱和。分析结果同时显示，气隙磁通密度最大可达1.9T，满足设计要求。

从式(4)可以看出，涡电流密度与磁场强度近似成正比关系，因此在瞬态仿真时须分析气隙磁通密度的影响因素。图7为当转速为1 000r/min时励磁电流对气隙磁通密度的影响曲线。由图可见：当励磁电流小于10A时，励磁电流和气隙磁通密度呈线性关系，当励磁电流继续增加时，气隙磁通密度的增加变缓，且磁路趋于饱和；同时，制动转矩变化趋势与气隙磁通密度相同，这也验证了要获得较大的制动转矩，必须得到较大的气隙磁通密度，但同时也要考虑空间条件的限制。

图8(a)为静态仿真时不同励磁电流下气隙磁通密度分布。由图可见，气隙磁通密度受到涡电流的影响，在凸极端面所对应的气隙平面的中间部分略有削弱，也说明此处涡流密度最大，当电流为26A时达到最大值1.9T。

图8(b)为不同速度时三维模型的气隙磁通密度分布。由图可见，气隙磁通密度一边减少，一边略有增加。原因是随着转速升高，由于涡流增大，涡流磁动势增大，导致气隙磁通密度减小部分更明显，平均气隙磁通密度就减小。

当励磁电流为26A时缓速器磁路达到饱和状态，励磁电流从26A增加至40A时其饱和程度不断增加，但是制动转矩仍缓慢增加。图9为励磁电流分别为40和26A时，饱和程度对磁场和制动转矩的影响。由图可见，当转速较低时(低于500r/min)，26和40A励磁电流下的制动转矩非常接近；随着转速的升高，涡电流密度增大，其反磁势亦增加，此时，两种励磁电流下的制动转矩区别明显，说明涡电流反磁势对于不同饱和程度的气隙磁通密度的削弱程度不同。

2.2 温度场分析

在温度场分析中，热源主要来自涡流损耗[18]，热源的边界条件为在集肤深度内热源强度，即生热率：

Q=P/V

(6)

式中：P为制动功率；V为涡流等效集肤深度的体积。

引入k-ε湍流模型[19]，湍动能k和耗散率ε的方程分别为

(7)

(8)

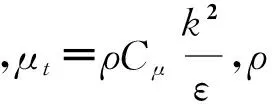
分析定子中的固体域，其能量方程[20]为

∂(ρh)/∂t=·(λT′)+SE

(9)

式中：h为定子的焓；λ为定子的导热率；T′为温度；SE为内热源；为梯度函数。

由于缓速器定子对称，所以建立了1/4模型，图10为瞬态定子共轭传热数值分析模型和对称边界条件。图11为制动时间为30s、制动功率为160kW、入口水的质量流量为4.5kg/s时瞬态温度分布，其定子内壁面的最高温度已达280℃。水道内水温达到90℃。约有90%的热量是通过水道底部的传导区域将热量传递给水，通过水散发出去。

2.3 发电系统

2.3.1 设计

发电机额定数据是按缓速器制动转矩为1 600N·m时设定的，以下主要对发电机主要参数确定、转子结构和励磁绕组的设计等进行论述与探讨。该永磁发电机利用缓速器内部空间，其永久磁铁安装于缓速器转子内壁。主要额定数据如表2所示。

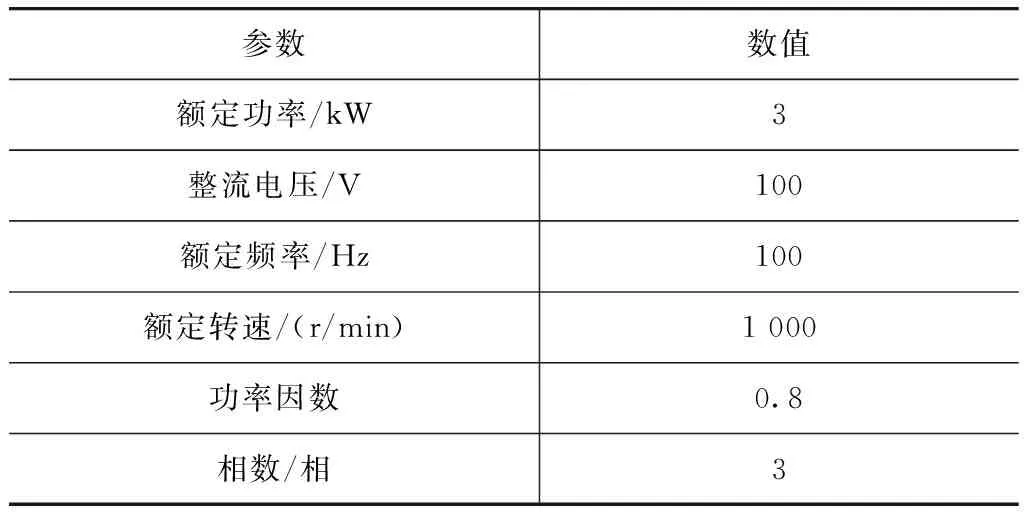
表2 发电机额定数据表

由发电机额定参数，可以计算得到其额定相电压Uφ=42V，额定相电流IN=30A，电机极对数pp=6。

发电机的转子铁芯内径R2和铁芯的长度l1与发电机的视在功率Sc、转速nN和发电机利用系数C有关。可根据式(10)估算出R2和l1。

(10)

式中：发电机视在功率Sc=mEIN×10-3；考虑到电机的用铜量，选取合理的主要尺寸比λ=l1/τ值，τ为极距。

该发电机为缓速器提供电源，其工作状态处于间断且短期。综合考虑发热和用铜量等因素，根据式(11)对每串联导体数，发电机转子内径等进行反复校正。

(11)

式中：m为永磁发电机相数；N为永磁发电机每相串联导体数；IN为永磁发电机电流；R2为永磁发电机转子内径。

发电机绕组采用单层同心式绕法，转子每极每相槽数q=1。q选定后根据式Z1=2pmq计算槽数。选择β=1，并由式(12)～式(14)算得绕组节距y1、绕组短距系数Kp和绕组分布系数Kd。

(12)

(13)

(14)

(15)

得每槽导体数，然后选取适当的漆包线，3根并绕。

再根据式(16)核算其绕组电流密度

(16)

式中：qa为单根导线截面积；Nt为导线总匝数。然后由AJ=Aja可得电机发热参数，选择漆包线的绝缘等级。

2.3.2 模型分析

由于永磁发电机磁力线在其内部径向闭合，因此采用二维瞬态数值模拟即可对其电磁场进行准确分析，占用计算机内存较小、用时较短。对永磁发电机部分取模型的1/12进行分析，边界条件采用反对称周期边界。图12为发电机数值模拟模型。

图13(a)为永磁发电机数值模拟外部电路。由于永磁发电机的外部负载为缓速器线圈，其阻值为3Ω，因此在数值模拟外电路中负载简化为3Ω电阻，模型设定转速n=1 000r/min。图13(b)和图13(c)分别为发电机空载和负载时的磁通密度分布云图。结果显示发电机气隙磁通密度为1.06T，验证了在发电机主体设计中，各部分磁通密度在合理范围之内。

3 实验研究

基于以上的分析结果，制作了缓速器样机，如图14所示。为测试缓速器制动特性、发电特性及自然特性，构建了试验平台，如图15所示。

3.1 制动特性

测试制动特性的目的是检测缓速器持续制动的能力，以便于进行分级控制。励磁电流由外部电源提供。图16为不同速度、不同电流下制动转矩仿真和实测结果。可以看出，仿真值与实测值误差在5%以内，验证了理论分析的正确性，而误差来源为模型简化、加工误差和温度上升的影响。制动转矩在转速为750r/min时基本达到稳定值，之后，制动转矩增加缓慢。

图17为持续制动特性。它显示了在持续制动一定时间时，温度和电流的变化对制动转矩的影响。图17(a)为励磁电流为30A时缓速器持续工作过程中温度和制动转矩随时间而变化的曲线。缓速器持续工作10min后，制动转矩下降了16.9%，温度由27.5℃上升到68℃。图17(b)为励磁电流恒为10A时，温度和制动转矩随时间的变化曲线。可以看出，缓速器持续工作10min后，制动转矩下降了4.7%，温度由41℃上升到85℃。图17(c)为恒温(72℃)和恒定励磁电流(10A)时，制动转矩随时间变化的曲线，可以看出，缓速器持续工作10min后，制动转矩变化很小，仅下降了0.5%。上述结果表明，温度和励磁电流是影响缓速器制动转矩的关键因素。

3.2 发电机特性

图18为永磁发电机二维瞬态场计算结果和实测数据的对比，包括空载特性、负载特性和外特性。可以看出，空载特性的仿真结果与实测数据非常吻合；而负载特性和外特性，仿真结果与实测数据的误差稍大，但变化趋势一致。在测试负载特性时，负载使用带电感的3Ω电阻，和缓速器线圈相同。缓速器工作时须要发电机提供励磁电流，最大为40A，结果表明设计满足要求。

3.3 自然特性

缓速器自然特性是指缓速器励磁电流由内部发电机提供时的制动特性。其仿真和实测结果如图19所示。由图可见，制动转矩随转速的升高而增大，符合设计要求。实测值与仿真值基本一致，误差在5%以内。

3.4 温度场分析

在转速为1 000r/min和制动转矩为1 600N·m的条件下测试温度场的分布。结果显示，定子内壁温度为255℃，水道中水温为72℃，仿真数据与实测结果相差约8.6%。缓速器工作产生的热量主要是从内表面向内部水道传递。缓速器制动转矩受电流大小的影响，当线圈通电时，线圈自身温度升高，而制动时由于受定子热辐射的影响，缓速器线圈温度进一步升高。

4 结论

(1) 分析发电系统和制动系统磁路结构，运用有限元法对新型自励式电磁液冷缓速器的发电系统和制动系统电磁场进行分析，应用有限体积法对缓速器瞬态流场-热场进行数值模拟，得出影响制动转矩的影响因素。

(2) 利用缓速器试验台架，对缓速器制动特性、发电系统特性和自然特性进行测试，并与仿真结果进行对比。

(3) 在持续工作时制动力矩热衰退在5%以下，制动转矩可达1 600N·m，满足重型车辆的要求。该系统已通过实车试验，效果良好。

[1]AnwarS.AParametricModelofanEddyCurrentElectricMachineforAutomotiveBrakingApplications[J].ControlSystemsTechnology,IEEETransactionsonEnergyConversion,2004,12(3):422-427.

[2] 沈海军,何仁,杨效军.自励时缓速器的设计与实验研究[J].汽车工程,2010,32(3):258-262.

[3]MogiShigeru.Retarder:Japan,JP7143732A[P].1993-11-17.

[4] 叶乐志.先进汽车缓速器与试验[M].北京:机械工业出版社,

2012:134-136.

[5]LiuCY,JiangKJ,ZhangY.DesignandUseofanEddyCurrentRetarderinanAutomobile[J].InternationalJournalofAutomotiveTechnology,2011,12(4):611-616.

[6]AlbertzD,DappenS,HennebergerG.Calculationofthe3dNonlinearEddyCurrentFieldinMovingConductorsandItsApplicationtoBrakingSystems[J].IEEETransactionsonMagnetics,1996,32(3):768-771.

[7]TakahashiN，NatsumedaM，MuramatsuK.OptimizationofPermanentMagnetTypeofRetarderUsing3dFiniteElementMethodandDirectSearchMethod[J].IEEETransactionsonMagnetics,1998,34(5):2996-2999.

[8]MuramatsuK,TakahashiN,MemberS. 3dEddyCurrentAnalysisinMovingConductorofPermanentMagnetTypeofRetarderUsingMovingCoordinateSystem[J].IEEETransactionsonEnergyConversion,1999,14(4):1312-1317.

[9]FujitaM,TokumasuT,YamadaT,etal. 3-dimensionalElectromagneticAnalysisandDesignofanEddy-currentRailBrakeSystem[J].IEEETransactionsonMagnetics,1998,34(5):3548-3551.

[10]HecquetM,BrochetP,LeeSJ,etal.ALinearEddyCurrentBrakingSystemDefinedbyFiniteElementMethod[J].IEEETransactionsonMagnetics,1999,35(3):1841-1844.

[11]NoguchiY,MiyaharaM,ImanishiK.Creep-fatigueLifePredictionforPermanentMagnetTypeEddyCurrentRetarder[J].JournaloftheSocietyofMaterialsScience,2004,53(7):795-800.

[12]AnwarS.AParametricModelofanEddyCurrentElectricMachineforAutomotiveBrakingApplications[J].ControlSystemsTechnology,IEEETransactionsonMagnetics,2004,12(3):422-427.

[13]GaySE,EhsaniM.ParametricAnalysisofEddy-currentBrakePerformancewithby3dFiniteElementAnalysis[J].IEEETransactionsonMagnetics,2006,42(2):319-328.

[14]SharifS,SharifK.InfluenceofSkinEffectonTorqueofCylindricalEddyCurrentBrake[C].InternationalConferenceonPowerEngineering,EnergyandElectricalDrives,2009:535-539.

[15]SrivastavaRK,KumarS.AnAlternativeApproachforCalculationofBrakingForceofanEddy-currentBrake[J].IEEETransactionsonMagnetics,2009,45(1):150-154.

[16]YeL,LiD,MaY,etal.DesignandPerformanceofaWater-CooledPermanentMagnetRetarderforHeavyVehicles[J].IEEETransactionsonEnergyConversion,2011,26(3):953-958.

[17]HofmannM,WerleT,PfeifferR,etal. 2Dand3DNumericalFieldComputationofEddy-CurrentBrakesforTraction[J].IEEETransactionsonMagnetics,2000,36(4):1758-1763.

[18] 叶乐志,李德胜,焦兵锋.水冷式永磁涡流制动装置的仿真与实验[J].机械工程学报,2011,47(10):101-105.

[19]LaunderBE,SpaldingDB.NumericalComputationofTurbulentFlows[J].ComputerMethodsinAppliedMechanicsandEngineering,1974,3(2):269-289.

[20]ANSYS.ANSYSCFXHelpDocument[DB/CD].2006.

Numerical Simulation and Experimental Study onSelf-excited Liquid-cooled Electromagnetic Retarder

Zhang Kai, Li Desheng, Yin Wanglei & Zheng Ran

CollegeofMechanicalEngineeringandAppliedElectronicTechnology,BeijingUniversityofTechnology,Beijing100124

In order to overcome the problem of severe thermal decay of braking torque in sustained braking of conventional eddy current retarder and save energy, a novel structure of liquid-cooled self-excited electromagnetic retarder is proposed. The electromagnetic field and the braking performance of the retarder are analyzed with finite element method and numerical simulations on its transient flow field and thermal field are conducted by using finite volume method. The characteristics of the retarder are also measured on a test bench. The results show that the simulated results well agree with test data with a braking torque up to 1,600N·m and its thermal decay less than 5% in continuous braking condition, meeting the requirements of heavy vehicles.

electromagnetic retarder; liquid-cooled; self-excited; numerical simulation; experimental study

*国家自然科学基金(51277005)资助。

原稿收到日期为2013年9月12日，修改稿收到日期为2013年12月23日。