基于声学模态的椭圆截面扩张腔声学分析*

王 伟，倪计民，李玉琦，金 晖

(1.奇瑞汽车有限公司发动机工程研究院，芜湖 241009； 2.同济大学汽车学院，上海 201804)



2015202

基于声学模态的椭圆截面扩张腔声学分析*

王 伟1，倪计民2，李玉琦1，金 晖1

(1.奇瑞汽车有限公司发动机工程研究院，芜湖 241009； 2.同济大学汽车学院，上海 201804)

利用马丢函数来求解椭圆双曲柱坐标系下的声波方程，获得声压的解析解，进而求得椭圆柱腔的声学模态，并利用声源激励法分析椭圆截面扩张腔的传递损失。与同截面积圆型扩张腔相比，椭圆截面扩张腔的传递损失在(2,1,n)偶阶模态处产生通过频率。将进、出口偏移至长轴(2,1,0)偶阶模态的波节线处，可消除(2,1,n)偶阶模态的影响；将进、出口偏移至短轴(0,2,0)偶阶模态的波节线处，可消除(0,2,n)偶阶模态的影响。

椭圆截面扩张腔；声学模态；传递损失；通过频率

前言

汽车消声器一般布置在汽车下方，它不仅要满足汽车动力性的要求，也要满足通过性的要求，在布置空间上受到限制，因此往往采用椭圆截面。对椭圆柱腔体的研究，最早源于电磁波的传播[1-3]。文献[4]中用有限元来分析椭圆截面扩张腔的声学性能。国内也有人利用有限元来研究进、出口位置对椭圆消声器传递损失的影响[5-6]。

本文中建立基于椭圆双曲柱坐标系的声波方程，利用初始条件和边界条件求解三维声学模态与频率，然后利用声源激励和模态叠加法，研究离心率和进、出口位置对传递损失的影响。

1 椭圆柱腔声学模态与传递损失

1.1 椭圆柱腔的声波方程和声学模态

为求解椭圆柱腔声波方程，引入椭圆双曲柱坐标系，如图1所示。基于椭圆双曲柱坐标系的声波方程[7]可描述为

(1)

式中：p为声压；h为半焦距；k0为波数；z为轴向变量；ξ为径向坐标，代表共焦椭圆族，0≤ξ≤∞；η为角坐标，代表共焦双曲线族，0≤η≤2π。ξ坐标与η坐标正交。定义椭圆的离心率e=h/a，a为椭圆长轴半径，而经推演得e=sech(ξ)。

利用分离变量法，声压变量可表示为

p(ξ,η,z,t)=Φ(ξ,η)Z(z)T(t)

(2)

式中：t为时间变量；Φ(ξ,η)是ξ和η的函数；Z(z)是轴向变量z的函数；T(t)是时间变量t的函数。

将式(2)代入式(1)，声波方程变为

(3)

假定Φ(ξ,η)=Ξ(ξ)Η(η)，其中Ξ(ξ)是ξ的函数，H(η)是η的函数。将Φ(ξ,η)代入式(3)，通过分离时间t和z轴变量后，可以得到：

d2H/dη2+(λ-q2cos2η)H=0

(4)

d2Ξ/dξ2-(λ-q2cosh2ξ)Ξ=0

(5)

式中：λ和q是本征值。式(4)称为马丢(Mathieu)方程，式(5)称为虚宗量马丢方程。

利用马丢方程，结合刚性壁面条件，可以得到周期方程(或称角频率方程)：

(6)

(7)

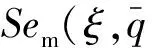
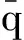
(8)

(9)

式中：c0为声速；L为柱腔的z轴向长度；n为对应z轴方向的模态阶数。

下面计算一具体椭圆截面柱腔的声学模态。椭圆截面长轴半径a=107.5mm，短轴半径b=70mm，离心率e=0.76，z轴长度L=150mm。利用式(6)和式(7)计算出偶模态和奇模态本征值，如表1所示。受篇幅所限，表1中最高本征值仅显示到(2,2)阶。在表1的基础上，利用式(8)和式(9)，计算出偶模态频率和奇模态频率，如表2所示。

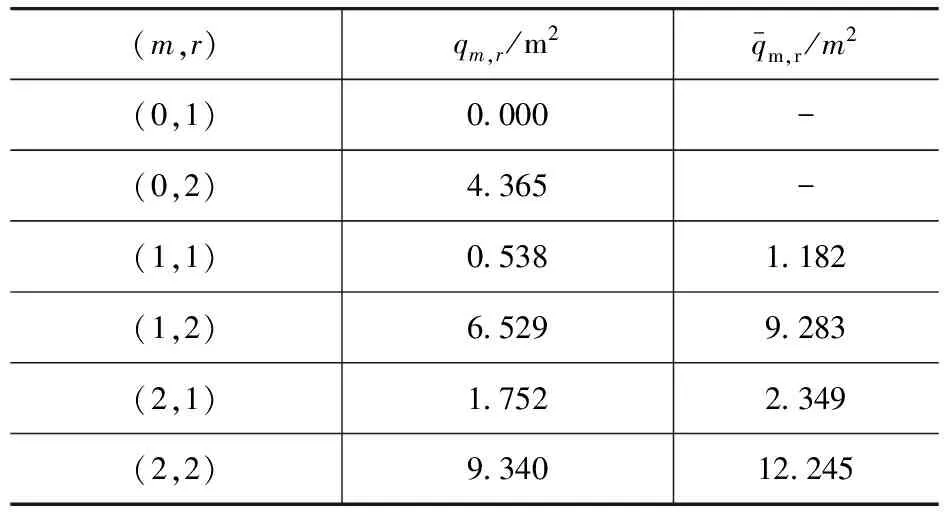
表1 本征值

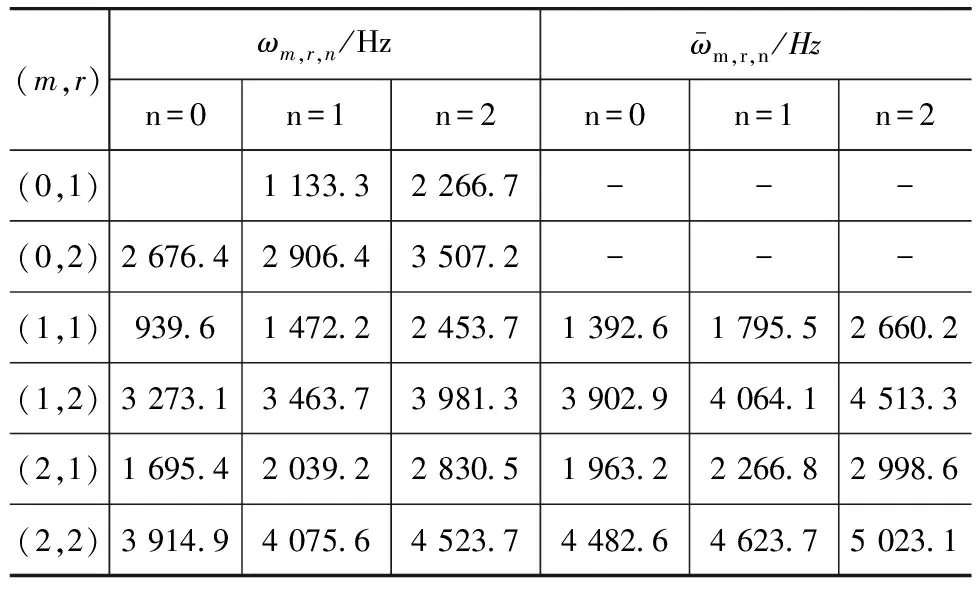
表2 模态频率

为理解椭圆截面的声学模态，利用声学有限元计算出偶、奇模态云图(振型)，分别如图2和图3所示。

1.2 基于声源激励法的传递损失

所谓点源激励就是在入口设置声源作为激励源，经过特定的声学空间，在出口获得声压值，利用出口声压和入口声源强度来计算系统的频率响应函数。一旦获得椭圆消声器的外形尺寸，那么利用模态叠加法，就可以获得椭圆腔的声学响应。根据谐波的特性，声腔入口与出口的声学变量之间的关系可以用四极子来表示：

(10)

式中：p和u分别表示声压和质点速度，下标1和2分别表示入口和出口。式(10)还可以转化为

(11)

式中Hij表示坐标i点的声压对坐标j点体积速度的频率响应函数。式(10)和式(11)中四极子参数的关系为

(12)

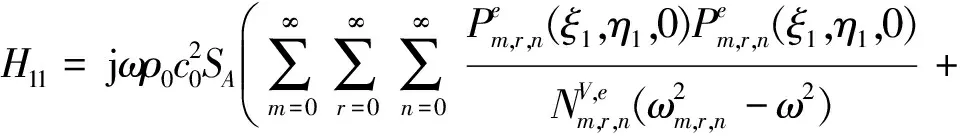
(13)

(14)

(15)

(16)

椭圆截面扩张腔的传递损失表达式为

(17)

2 椭圆截面扩张腔消声特性分析

2.1 通过频率

将1.1节提到的椭圆柱腔连接半径为20mm的进出口管后，变成椭圆截面扩张腔。利用声源激励法计算它的传递损失，结果如图4所示。为了便于分析，图4上标注了声学模态阶数，其中模态标签中的“E”指偶模态，“O”指奇模态。E(0,1,2)阶模态频率与O(2,1,1)阶模态频率重合，频率越高，这种模态频率重合现象越多，因此本文中主要研究低价模态对消声性能的影响。从图4中可以看出，E(0,1,1)阶、E(2,1,0)阶、E(2,1,1)阶和E(0,1,2)阶模态频率成为传递损失的通过频率。(1,1,0)阶和(1,1,1)阶不管偶模态还是奇模态，都未产生通过频率；(2,1,1)阶和(2,1,2)阶的奇模态也未产生通过频率。E(0,1,1)阶和E(0,1,2)阶是两个典型的轴向模态，它由腔体轴向长度决定。对照图2和图3，未产生通过频率的模态云图原点都是波节区，而(2,1,n)偶阶模态位于波腹区。结合模态理论，当扩张腔入口位于某阶模态的波节区时，该阶模态无法被激发；如果扩张腔出口位于某阶模态的波节区，则该阶模态的影响被极大衰减。

2.2 离心率对传递损失的影响

离心率是椭圆本征的一个重要参数。本节对截面积相等，离心率不同的椭圆扩张腔进行传递损失的研究。圆是椭圆的一种特殊形式，它的离心率是0，加入0.5离心率的方案，结合前文中已有0.76离心率的方案，共有3种离心率方案，详见表3。

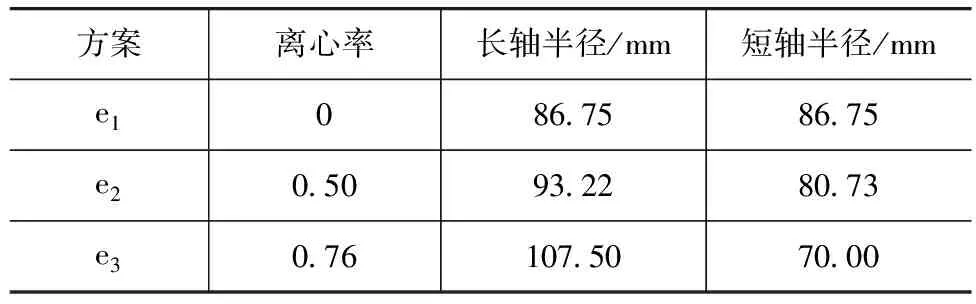
表3 离心率方案

图5对比3种不同离心率扩张腔的传递损失。E(0,1,n)模态作为轴向模态，对应的通过频率不受离心率的影响。随着离心率的降低，同阶模态频率升高，同阶偶模态和奇模态频率也越来越接近。对于e3方案，E(2,1,0)阶模态通过频率影响周围频率的传递损失；但对于e2方案，偶模态和奇模态频率由于比较接近，较窄的频率范围受E(2,1,0)阶通过频率的影响。而对于圆形截面方案，偶模态和奇模态频率完全一致，此时(2,1,0)阶模态原点完全变为波节区，此模态不会产生通过频率。如果用圆形截面代替椭圆截面进行扩张腔传递损失计算，会漏掉一些通过频率。同等截面积条件下，圆形截面扩张腔的消声性能最好。

2.3 进出口位置对传递损失的影响

根据模态理论，如果将入口或出口放置在E(2,1,0)阶或E(0,2,0)阶的波节线上，则可消除这些模态产生的通过频率。对于E(2,1,0)阶模态，位于长轴上的波节点与原点距离约为45mm；对于(0，2，0)阶模态，位于短轴上的波节点与原点的距离约为36mm[8]。图6显示4种不同的进、出口布置方式，方案1与2.2节方案e3相同。

图7对比了出口偏置对传递损失的影响。方案2的出口偏置到E(2,1,0)阶模态的波节线上，不但消除E(2,1,n)低阶模态通过频率的影响，还在E(1,1,n)低阶模态处产生共振峰值，增强消声效果。方案3的出口偏置到E(0,2,0)阶模态的波节线上，它消除了E(0,2,n)低阶通过频率的影响，同时还增强O(1,1,n)低阶模态处的消声效果。方案2对低频通过频率的消除作用明显。

图8显示了进、出口同时偏置对传递损失的影响。方案4进口偏移到(2,1,0)阶模态的波节线上，出口偏移到(0,2,0)阶模态的波节线上。它兼顾了方案2和方案3的优点，在3 000Hz范围内，消除了除E(0,1,n)轴向低阶模态之外其他模态产生的通过频率。而E(0,1,n)轴向低阶模态产生的通过频率，可通过采用内插管的方式来消除。

3 试验分析

利用消声器插入损失试验对前面的模拟结果进行分析。试验台架系统如图9所示，噪声测试仪器为ND2型精密声级计。

试验仅对2.2节的方案e1和2.3节的方案1和方案4进行对比，如图10所示。3个消声器在1 250Hz以前的中心频率带，插入损失相同。方案1中，消声器受E(2,1,0)和E(2,1,1)阶模态影响，1 600和2 000Hz中心频率处消声量降低。方案4中，提高1 600和2 000Hz中心频率的消声量，达到圆形截面消声器的水平。另外，方案4消除了传递损失在2 300～3 000Hz内的通过频率，其插入损失在2 500Hz的消声量得到提升。

4 结论

相比圆形截面，基于椭圆截面的扩张腔会产生更多的通过频率，降低消声性能。但是通过研究声学模态，如果将进、出口设置在低价通过模态频率的波节线上，则可消除该模态通过频率的影响。

[1] Wang B K, Lam K Y, et al. Elliptical Waveguide Analysis Using Improved Polynomial Approximation[J]. IEEE Proceedings, Microwaves, Antennas and Propagation,1994,141(7):483-488.

[2] Caorsi S, Pastorino M, Rafetto M. Electromagnetic Scattering by a Multilayer Elliptic Cylinder Under Transverse-magnetic Illumination: Series Solution in Terms of Mathieu Functions[J]. IEEE Transactions on Antennas and Propagation,1997,45(2):926-935.

[3] Hussein A M, Wurjaranta W. Analysis of Elliptic Conductors Using the Point Matching Method with Mathieu Functions[J]. IEEE Transactions of Magnetics,1997,33(5):4125-4127.

[4] Denia F D, Alberlda J, Fuenmayor F J, et al. Acoustic Behavior of Elliptical Chamber Mufflers[J]. Journal of Sound and Vibration,2000,241(10):401-421.

[5] 方智,季振林.进出口位置对不同形状膨胀腔消声特性的影响[J].噪声与振动控制,2011(4):160-164.

[6] 江小亮,李以农.椭圆截面扩张式消声器消声特性的有限元分析[J].汽车工程师,2013(1):27-28.

[7] Hong K, Kim J. Natural Mode Analysis of Hollow and Annular Elliptical Cylindrical Cavities[J]. Journal of Sound and Vibration,1995,183(2):327-351.

[8] 王伟.排气系统声学性能与流动性能的理论研究[D].上海:同济大学,2007.

Acoustic Analysis on the Expansion Chambers withElliptical Cross-section Based on Acoustic Modes

Wang Wei1, Ni Jimin2, Li Yuqi1& Jin Hui1

1.EngineEngineeringResearchInstitute,CheryAutomobileCompany,Wuhu241009;2.SchoolofAutomotiveStudies,TongjiUniversity,Shanghai201804

Mathieu function is used to solve the sound wave equation under elliptic-hyperbolic cylindrical coordinate with the analytical solutions of sound pressure obtained. The acoustic modes of cylindrical chambers with elliptical cross section are further acquired and sound source excitation method is employed to analyze the transmission loss of expansion chamber. Compared with expansion chamber with round cross section of same area, the transmission loss of expansion chamber with elliptical cross section generates passing frequency at even mode (2,1,n). With its inlet and outlet moving onto the nodal line of even mode (2,1,0) on the major axis of expansion chamber, the effects of even mode (2,1,n) can be eliminated; while with its inlet and outlet moving onto the nodal line of even mode (0,2,0) on the minor axis of expansion chamber, the effects of even mode (0,2,n) can be eliminated.

expansion chamber with elliptical section; acoustic modes; transmission loss; passing frequency

*国家863计划项目(2008AA11A148)资助。

原稿收到日期为2013年8月29日，修改稿收到日期为2013年12月9日。