基于天棚控制的半主动悬架建模及稳定性分析*

庞 辉，付文强,刘 凯,李 强

(西安理工大学机械与精密仪器工程学院，西安 710048)



2015199

基于天棚控制的半主动悬架建模及稳定性分析*

庞 辉，付文强,刘 凯,李 强

(西安理工大学机械与精密仪器工程学院，西安 710048)

为探究时滞因素对开关天棚控制半主动悬架动态稳定特性的影响，以含时滞的开关天棚控制半主动悬架模型和时滞微分方程理论为基础，并运用Lyapunov稳定性理论，提出该悬架控制系统失稳临界时滞求解的理论分析和数值计算方法；利用数值解法求得不同被动基值阻尼和可切换阻尼减振器阻尼系数下悬架系统的失稳临界时滞量及全(非全)时滞渐进稳定域；最后，通过建立含时滞开关天棚控制半主动悬架系统仿真模型，分析得到时滞对半主动悬架动特性的影响规律。结果表明，当时滞量达到临界值时，悬架系统稳定性将严重恶化。本研究为含时滞开关天棚控制可切换阻尼半主动悬架控制系统的时滞补偿及其稳定性控制策略的制定奠定基础。

半主动悬架；时滞；天棚控制；稳定性

前言

近年来，磁流变阻尼器半主动悬架系统的研究与应用受到国内外广泛关注。基于天棚阻尼控制的磁流变阻尼器半主动悬架因其控制简单，能耗低，阻尼可调节，性能可靠，且通过合理选择相关参数，可消除悬架系统共振现象，对改善车辆乘坐平顺性、操纵稳定性和行驶安全性均具有重要作用，在各型车辆上均有广泛应用[1]。

天棚阻尼控制是半主动悬架的经典算法[2]，可根据悬架的相对速度和车身绝对速度的符号来切换软硬阻尼设置，从而对半主动悬架进行最优的反馈控制，具有结构简单、性能可靠，能耗低、阻尼切换速度快、工程控制易于实现等优点[3]，但是，由于天棚开关控制的半主动隔振系统具有时延性，未能很好地解决操纵稳定性问题。作为控制系统不可避免的时滞问题，其时滞因素包括：由传导线和A/D、D/A转换装置产生的传输时滞、振动结构的阻尼时滞、控制器建立控制并计算控制律所引起的计算时滞和作动器的反应时滞等[4]。基于天棚开关控制，半主动悬架作为控制阻尼力可变的自反馈控制系统，时滞因素的叠加效应对悬架性能的影响更加明显，严重时可导致半主动悬架系统丧失运动稳定性，出现影响行驶安全的轮跳现象等悬架失稳问题。

目前，国内外学者对含有时滞的半主动控制悬架开展了大量研究[5-10]，主要聚焦于悬架迟滞非线性特性对汽车平顺性影响规律等方面的研究，而对考虑时滞的天棚开关控制半主动悬架系统的失稳机制和建模分析则少有讨论。为此，本文中以考虑时滞影响下的天棚开关控制1/4车辆模型为研究对象，首先建立含时滞半主动控制策略下的悬架数学模型，推导出悬架振动系统的时滞运动微分方程，通过分析得到含时滞悬架振动系统的临界失稳条件、失稳机理及其精确数值解；然后，通过数值仿真分析含时滞天棚开关控制半主动悬架系统的被动基值阻尼系数、减振器“开”状态阻尼系数和临界失稳时滞时间的变化规律；最后得到路面激励下时滞对悬架动态稳定特性的影响规律。

1 含时滞半主动悬架模型与动力学方程

1.1 含时滞1/4车辆悬架

[11]，建立了汽车1/4车辆含时滞实际天棚开关控制半主动悬架系统力学模型简图，如图1所示。半主动悬架设计的目的是改善车辆的动特性，故要求该模型可精确地模拟分析车辆的垂向动力学特性并考虑悬架系统的时滞因素，车辆及其半主动悬架相关的等效参数见表1。

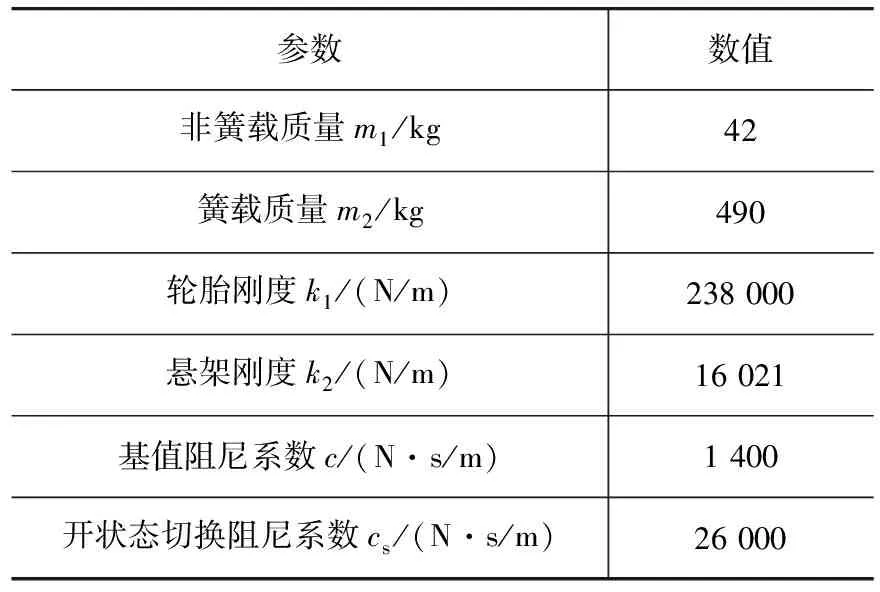
表1 2自由度半主动悬架参数

1.2 含时滞悬架动力学方程

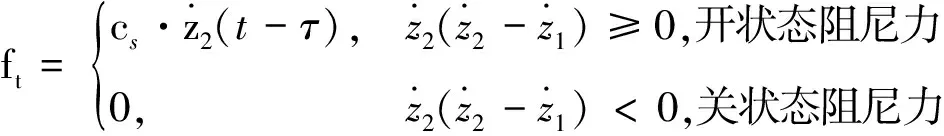
(1)

考虑时滞量τ对悬架系统的影响，式(2)加入了时滞项，由达朗伯原理可得天棚控制可切换阻尼的半主动悬架系统的“开”状态单时滞运动微分方程[7]为

(2)

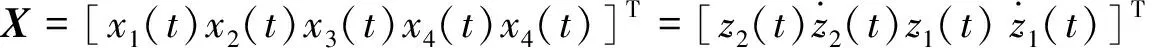
(3)

其中：

2 半主动悬架系统时滞稳定性理论分析

根据含时滞的常系数线性系统微分方程理论[12]，式(2)的通解形式为

zr(t)=Xreλt，r=1,2

(4)

式中：Xr为zr经过拉氏变换的变量解；λ为特征值。将此通解带入式(2)，推导整理得到该齐次微分方程组所对应的特征方程形式如式(5)所示，并由微分方程组式(2)非零实数解条件，得到式(5)恒等为零。

(5)

由线性常系数时不变微分方程的Lyapunov稳定性判据[13]可知，时滞系统渐进稳定的充要条件是式(5)系统特征方程的全部特征根均为负实数，或者具有负实部的共轭复根(系统传递函数所有极点必须位于[s]平面左半部，线性系统才稳定)，故系统临界失稳的条件是式(5)仅有纯虚根λ，假设λ=jω，系统将呈现以固有频率ω为基频的自激振动，将特征根λ=jω代入式(5)，并利用欧拉公式分离其实部与虚部，可得式(5)仅有纯虚根的条件为

(6)

经过化简可得

X=m1m2ω4-(m2k1+m2k2+m1k2)ω2+

k1k2=0

(7)

Y= [k1-(m1+m2)ω2]·[c+cs(sin(ωτ)-

cos(ωτ))]·ω=0

(8)

为求得时滞系统临界失稳时滞量，式(8)应满足无复数根条件，可得到仅含自激振动频率ω的最简高次多项式为

b2ω4+b1ω2+b0=0

(9)

式中：b2，b1和b0分别为与悬架等效参数相关的多项式系数。

通过Matlab数值求解得式(9)的精确实根解ω，将该ω代入式(8)中即可解出该悬架系统失稳的临界时滞量τc。由式(8)可知，适当选择一定范围的悬架系统参数，可使基频ω无实根，则系统失稳的临界条件不复存在，悬架系统对于任意时滞恒稳定，由式(9)求得系统自激振动基频为ω=+4.5227Hz，由式(8)可得

(10)

根据悬架参数表1中数值，求得该天棚阻尼控制半主动悬架系统临界失稳时滞量的精确数值解，并通过Matlab数值求解得到在基值阻尼系数(0～4 200)和天棚开状态切换阻尼系数 (0～+25000)范围内存在临界时滞量τ1=0.4266s，τ2=0.1422s和τ3=0.2415s，其分别表示满足式(10)的特征数值解。

3 数值仿真

根据所建立的含时滞悬架模型和选用的天棚控制半主动悬架控制策略，本文中通过仿真分析在Matlab中对该悬架系统的临界时滞量τc进行数值求解，分析悬架基值阻尼c与天棚开状态切换阻尼cs对时滞(非)稳定区的影响规律，并且根据求解所得临界时滞量τc，在Simulink中建立考虑时滞的1/4车辆半主动悬架模型，通过仿真分析可得：①被动悬架控制；②不考虑时滞控制(时滞量τ=0)；③临界失稳时滞量τ3=0.2415s3种情形下时滞因素对悬架系统动力特性的影响规律，最终分析可得时滞量τ与悬架稳定性的变化曲线。

3.1 基值阻尼与天棚开状态切换阻尼的悬架稳定性分析

根据式(9)和式(10)以及表1中前4个参数值，利用Matlab求解悬架系统中不同基值阻尼c和天棚开状态切换阻尼cs情形下的临界失稳时滞量[14]τc，结果如图2所示。

由图可见：

(1) 悬架系统参数范围一定时，超过时滞曲线0.426 6s的临界时滞量τc代表悬架系统是全时滞渐进稳定的，表示在时滞因素影响下，悬架系统丧失运动稳定性后重获动态稳定性的系统特征时滞量转折点，各时滞量曲线分别表示悬架系统非全时滞稳定域(0.142 2～0.426 6s)内临界失稳的边界曲线；

(2) 由式(10)和图2可得，当悬架系统参数一定，并且天棚开状态切换阻尼cs调节范围确定时，在基值阻尼c确定的情形下，天棚开状态切换阻尼cs增大，系统临界时滞量τc减小，并且对于给定的天棚开状态切换阻尼cs，随着基值阻尼c的增大，临界时滞量τc增大，当天棚开状态切换阻尼cs足够小、基值阻尼c足够大且基值阻尼c大于天棚开状态切换阻尼cs时，悬架系统将快速进入全时滞渐进稳定区域；

(3) 为了更加清晰地说明被动基值阻尼c与天棚开状态切换阻尼cs平面内的全(非全)时滞渐进稳定区域，同样基于式(9)和式(10)求解，可另外得到图3和图4的曲线。

图3示出在基值阻尼系数c，天棚开状态切换阻尼cs平面上，全时滞稳定性3个不同区域，即非全时滞渐进稳定区域Ⅰ区、全时滞非稳定区域Ⅱ区和全时滞渐进稳定多域Ⅲ区的划分，由图中可以看到基值阻尼c、天棚开状态切换阻尼cs对全时滞稳定性区域的影响[15]。

图4则示出全时滞稳定性区域在临界时滞量曲面上的划分。由图可明显看出，临界时滞量τc与基值阻尼c和天棚开状态切换阻尼cs之间的关系。天棚开状态切换阻尼cs确定时，随着基值阻尼c的增大，临界时滞量τc减小；但当基值阻尼c足够大(约大于5 000N·s/m)时，系统进入全时滞渐进稳定Ⅲ区，临界时滞量τc将随基值阻尼c的增大而迅速增加。Ⅲ区时滞量明显大于Ⅰ区，在该区域内悬架系统天棚开状态切换阻尼cs变化范围较小，时滞通道受限，而系统临界时滞量τc非线性增加并稳定存在，使得悬架系统在所属(c，cs)区域内能够避免出现振动失稳现象， 即便意外时滞失稳也能最快恢复稳定态。

图4中Ⅱ区为悬架系统全时滞非稳定区域，悬架系统Ⅱ区的时滞量最小，该区内悬架天棚阻尼开状态切换时，悬架基值阻尼c、天棚开状态切换阻尼cs比重呈此消彼长变化，而其临界失稳时滞量τc呈现出一定的非线性随机不稳定性，使悬架系统实际时滞量极易超过其最小临界时滞(量)稳定裕度，导致系统意外失稳，出现较危险的轮跳现象；同时，悬架系统也会因时滞速度通道开关状态阻尼切换而发生畸变，呈现出对微扰动极为敏感的混沌失稳现象，这都将恶化车辆操纵稳定性、行驶安全性和乘坐舒适性。

图4中Ⅰ区为悬架系统非全时滞渐进稳定区域，Ⅰ区临界时滞量大小介于Ⅱ区和Ⅲ区之间，跨度最大，区内悬架天棚开状态切换阻尼cs变化范围增大，时滞通道充分放大，而该特定区域内，悬架保持稳定性的最小临界时滞(量)稳定裕度呈类线性比例稳定存在，在各类时滞叠加影响下，悬架系统实际时滞容易大于其最小临界时滞(量)稳定裕度，因而可能出现悬架失稳现象。

3.2 路面激励下时滞对悬架动特性影响分析

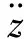
根据表1给定的悬架系统参数，可采用时域均方根法来分析汽车悬架结构振动性能的动态评价指标。通过对比分析被动悬架、不考虑时滞因素影响(时滞量τ=0)，考虑时滞因素影响(临界时滞量τ3=0.2415s)时的天棚阻尼半主动悬架控制系统的动特性时域曲线、时滞量(τ=0～0.65s)范围内时滞量与悬架运动稳定性变化曲线及数理统计结果分别如图6～图8、图9～图11和表2所示。

通过分析曲线和数据可得如下结论。

(1)时滞时间量作为影响天棚阻尼控制半主动悬架系统的客观因素，对于悬架动特性的影响表现不一。与被动控制悬架相比，时滞量τ的增加总会增大轮胎动载荷，恶化悬架系统的运动安全性；时滞对于车身加速度、悬架动行程均有一定程度地振荡衰减作用，直至渐进临界时滞量(τ3=0.2415s)，时滞将全面恶化半主动悬架系统的动态特性，导致悬架系统意外失稳。

(2)时滞能够振荡减小车身加速度，可改善车辆行驶平顺性，直至临界时滞量，时滞将使得车身加速度振动幅值剧增，严重恶化车辆的乘坐舒适性。

(3)悬架动挠度并不随时滞量τ的增大而呈现单调变化，在临界失稳时滞时刻，时滞使得悬架动挠度值激增，将严重恶化车辆操纵稳定性。

(4)时滞会恶化轮胎-路面附着效果，至临界时滞量时，轮胎附着效果变差并产生周期性跳动现象，并且随时滞量的增大，轮跳周期缩短而幅值波动变化，轮胎丧失良好的抓地性能，车辆行驶安全性被严重破坏。

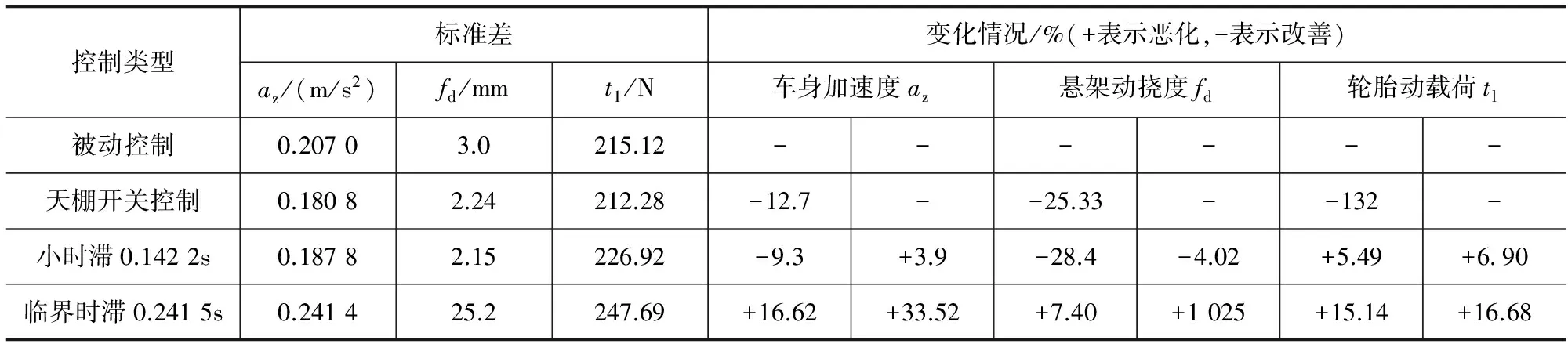
表2 随机路面激励下时滞对半主动悬架动特性影响统计

注：表中车身加速度、悬架动挠度和轮胎动载荷的变化各有两栏数据，其中，第1栏表示相对被动控制变化的百分比；第2栏则表示相对天棚开关控制变化的百分比。

(5)由图9～图11所示时滞时间与悬架运动稳定性变化曲线可知，因时滞时间的存在，车身加速度、悬架动挠度、轮胎动载荷均会随着临界失稳时滞量的出现而呈现出剧烈增加趋势直至最大，悬架运动稳定性严重破坏，当时滞量(τ≥0.4266s)为渐进稳定时滞时刻时，三者呈现周期性波动，其幅值变化周期缩短而峰值衰减，车辆悬架系统丧失运动稳定性后逐渐恢复稳定。

(6)时滞总是会恶化车辆行驶安全性，在临界失稳时滞量处，悬架系统全面丧失运动稳定性，伴随含时滞悬架系统渐进稳定时滞量(τ1=0.4266s)的出现，悬架振动系统由此重新进入渐进稳定平衡态。

(7)相较于不考虑时滞的天棚开关控制半主动悬架控制系统(τ=0)，时滞因素(临界时滞τ3=0.2415s)对悬架性能的影响遵从上述(2)～(5)保持不变；在现实条件下，时滞作为直接影响悬架运动性能的客观因素，将时滞量τ限定在较小范围内，可使悬架系统具有较好的平顺性，对改善车辆操纵稳定性、安全性及轮胎附着性能有一定的现实意义。

4 结论

本文中基于含时滞的1/4车辆天棚开关控制半主动悬架动力学模型，结合理论分析、数值求解与仿真实验，分别给出了悬架系统临界时滞量τc与基值阻尼c、天棚开状态切换阻尼cs之间的关系，讨论了含时滞天棚开关控制半主动悬架控制系统的时滞渐进稳定性机理，获得了时滞因素对天棚控制半主动悬架系统动特性及悬架动态稳定性的影响规律，为解决悬架系统时滞预估补偿策略的研究奠定了坚实基础。

参考文献

[1] 贾永枢，周孔亢，徐兴,等. 汽车单筒充气磁流变减振器特性的试验研究[J]. 汽车技术, 2013, 3(1/2): 51-54.

[2] 赵研, 寇发荣, 方宗德.汽车天棚控制半主动悬架模型仿真与性能分析[J]. 计算机仿真，2006,23(11):233-236.

[3] 任宏斌,陈思忠,冯占宗.基于天棚On-Off控制的磁流变半主动悬架研究[J]. 北京理工大学学报，2014,34(2):148-152.

[4] 汪若尘, 陈龙, 江浩斌.基于多项式判别理论时滞半主动悬架稳定性研究[J]. 中国机械工程，2006,17(24):2628-2630.

[5] 陈龙, 汪若尘, 江浩斌.含时滞半主动悬架及其控制系统[J]. 机械工程学报，2006,42(1):130-133.

[6] 闻邦椿. 机械振动学[M]. 北京：冶金工业出版社，2011.

[7] 陈龙, 汪若尘, 江浩斌,等. 半主动悬架及其控制系统的时滞控制研究[J]. 中国机械工程，2005,16(24):2249-2252.

[8] 方明霞, 谈军, 冯奇. 悬架迟滞非线性特性对汽车平顺性的影响[J]. 振动与冲击，2008,27(11):67-70,199.

[9] 董小闵, 余淼, 廖昌荣,等. 具有非线性时滞的汽车磁流变悬架系统自适应模糊滑模控制[J]. 振动与冲击，2009, 28(11):55-60.

[10] 申永军, 祁玉玲, 杨绍普,等. 含时滞的单自由度半主动悬架系统的动力学分析[J]. 振动与冲击，2012,31(24):38-40.

[11] 余志生. 汽车理论[M]. 5版.北京：机械工业出版社，2009.

[12] 秦元勋,刘永清,王联,等. 带有时滞的动力系统的稳定[M].2版. 北京: 科学出版社, 1989.

[13]KatsuhikoOgata.现代控制工程[M].4版.北京: 电子工业出版社, 2003.

[14]JanseVanRensburgN,SteynJL,ElsPS.TimeDelayinaSemi-activeDamper:ModellingtheBypassValve[J].JournalofTerramechanics, 2002, 1: 35-45.

[15]PalkovicsL,VenhovensPJT.InvestigationonStabilityandPossibleChaoticMotionsintheControlledWheelSuspensionSystem[J].VehicleSystemDynamics, 1992,21: 269-296.

Modeling and Stability Analysis of Semi-Active Suspension with Sky-hook Control

Pang Hui, Fu Wenqiang, Liu Kai & Li Qiang

SchoolofMechanicalandPrecisionInstrumentEngineering,Xi’anUniversityofTechnology,Xi’an710048

For investigating the effects of time delay factor on the dynamic stability characteristics of semi-active suspension with switch sky-hook control, based on semi-active suspension model with time-delay switch sky-hook control and the theory of delay differential equations, and by applying Lyapunov stability theory, the methods of theoretical analysis and numerical calculation are proposed to find the critical time delay of that suspension control system. Then with the methods, the critical time delay resulting in instability and the asymptotic stability region of non-arbitrary and arbitrary time delay of suspension system are obtained under different passive damping and the damping coefficients of shock absorber with switchable damping. Finally, a simulation model for the switch sky-hook control semi-active suspension with time delay is built, and the rules of the effects of time delay on the dynamic characteristics of semi-active suspension are analyzed. The results show that the stability of semi-active suspension will seriously deteriorate when time delay approaches its critical value. This study lays a foundation for setting up the strategies of time-delay compensation and stability control for the semi-active suspension control system with time delay switch skyhook damping control.

semi-active suspension; time delay; skyhook control; stability

*国家自然科学基金(51305342)、陕西省自然科学基金(2014JQ7240)、陕西省教育厅科研计划项目(2013JK1027)和校博士科研计划(102-211204)资助。

原稿收到日期为2015年7月2日，修改稿收到日期为2015年8月19日。