灰色Markov模型动态关联规则趋势度挖掘方法
张忠林,石皓尹,闫光辉
兰州交通大学 电子与信息工程学院,兰州 730070
1 引言
关联规则挖掘是数据挖掘中重要的研究方法[1],主要用于发现事物数据集中项与项之间的关系。由于事务数据通常具有时间特性[2],提出了考虑时间因素的序列模式挖掘;为了描述关联规则随时间变化的特点,提出了动态关联规则的定义[3];在以上基础上进一步改进了动态关联规则的定义及挖掘算法[4-5];对动态关联规则元规则进行挖掘[6],可以得到规则在基于时间序列上的变化情况[7];为了提高动态关联规则的挖掘质量,文献[8]提出了动态关联规则趋势度的概念,从而更好地反映规则随时间变化的动态信息。本文在以上研究的基础上提出了一种将灰色-Markov模型应用在动态关联规则趋势度挖掘的方法。该方法在避免生成无用的动态关联规则的基础上,挖掘出满足趋势度阈值的规则,提高了挖掘的效率,使挖掘出的动态关联规则更加全面可靠,并同时解决如何选取趋势度阈值的问题。
2 动态关联规则
动态关联规则能描述自身特性随时间的变化,而支持度和置信度在时间上构成的向量可以反映关联规则在时间上的变化趋势。描述如下:
设I={i1,i2,…,in}是项集合,数据集D是在时间段t内收集到的,t为相等不相交的长度为n的时间序列,即有t={t1,t2,…,tn}。根据时间段的划分,将数据集D分为n个子数据集,其中数据子集Di(i∈{1,2,…,n})是在ti(i∈{1,2,…,n})时间段内收集的项集T满足T⊆I。若A和B为项集,A⊂I,B⊂I,并且A∩B=∅ 。关联规则A⇒B在D中的支持度Support是事务集D中包含A∪B的百分比,有:Support(A⇒B)=P(A∪B),关联规则A⇒B在D中的置信度Confidence是事务集D中A事务发生的条件下B事务发生的百分比,有Confidence(A⇒B)=P(A|B)。有如下相关定义:
定义1支持度向量(SV)是动态关联规则A⇒B(或者项集A∪B)的向量,有如下表示形式:
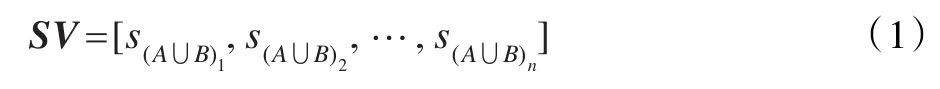
定义2设项集A∪B的支持度为s,则:

其中,M是D中的事务数。项集的支持度向量为SV=[f1,f2,…,fn]。
定义3动态关联规则A⇒B的置信度向量具有以下的表示形式:

动态关联规则可以表述为:具有支持度向量SV、置信度向量CV、支持度s、置信度c四个参数的关联规则;表示形式为:A⇒B(SV,CV,s,c)。
动态关联规则引入支持度向量以及置信度向量后,根据趋势的变化可以得到动态关联规则趋势度的定义。关于动态关联规则趋势度的具体定义本文不再阐述和说明,参见文献[8]中定义1至定义8。
3 灰色-Markov模型
3.1 GM(1,1)预测模型
邓聚龙教授于1982年首次提出了灰色系统理论。灰色系统理论是建立系统运行趋势模型的有效理论方法[9-10]。灰色系统理论适用于动态预测,且只需少量已知信息就可建立预测模型[11]。灰色GM(1,1)预测模型的具体步骤如下所示。

(2)按照GM(1,1)建模过程可得:

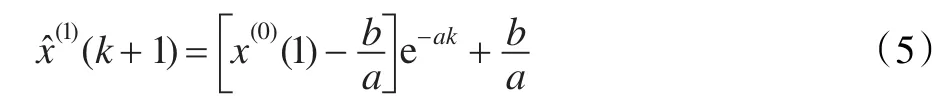

其中:
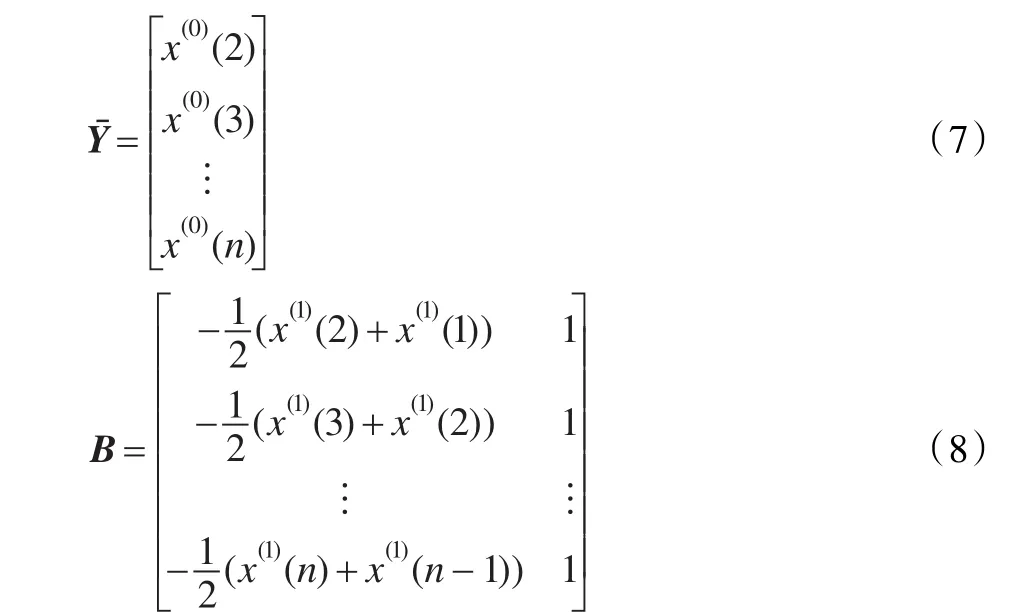
(4)把估计值a、b代入式(5)中得到时间影响方程:

当t=1,2,…,n-1时,由式(9)得到的是拟合值,而当k≥n时,得到的是预测值。
(5)对序列x^(1)(k+1)做累减还原处理可得原始数据预测。公式:



其中n为序列x(0)的长度。发展系数 -a是GM(1,1)模型适用性范围的标准,模型适用范围与发展系数 -a相关[12-13],如表1所示。

表1 GM(1,1)模型适用范围表
3.2 Markov链及其转移概率矩阵
马尔科夫链适用于波动较大的动态过程[14-15],在这一点上恰恰可以弥补灰色预测的局限性。
设{Xn,n∈T}为随机过程,若对于任意的整数n∈T和任意的状态i0,i1,…,in+1∈I,条件概率满足:P(Xn+1=in+1|X0=i0,X1=i1,…,Xn=in)=P(Xn+1=in+1|Xn=in),则 称{Xn,n∈T}为马尔科夫链。马尔科夫链具有无后效性,它表示系统未来(t=n+1)所处的状态仅与其现在(t=n)所处的状态有关,而与其过去(t≤n-1)所处的状态无关。设Ei是系统在时间t所处的状态,Xn是与状态空间相对应,并形成了Markov链。对任意的n∈T和状态i,j∈I,称pij(n)=P(Xn+1=j|Xn=i)为马尔科夫链的转移概率,表示系统在i状态条件下向状态j转换的概率。由pij可得系统状态的转移概率矩阵:


4 算法过程描述
目前最常用到的不确定性系统的研究方法主要有:概率统计、模糊数学和灰色系统理论,这三种方法的共同点是研究对象都具有某种不确定性。但是正是研究对象在不确定性上的区别,才产生了这三种各有特色的不确定性科学:模糊数学着重研究“认知不确定”的问题,主要通过借助于隶属函数进行处理;概率统计研究的是“随即不确定”现象,着重于现象的统计规律。其出发点是大样本,并且要求对象服从某种典型的分布。而本文所采用的灰色系统理论着重研究以上两种方法难以解决的“小样本”、“贫信息”的不确定性问题。灰色系统理论最重要的特点也是它最大的优点就是“少数据建模”,因此在原始数据非常少的情况下,使用灰色系统理论进行建模以及预测结果的准确度会高于其他方法,这正是本文采用灰色系统来建模的原因。
灰色系统理论中的GM(1,1)模型可以在原始数据非常少的情况下进行建模,而且还可以得到精度较高的结果。但是通过对GM(1,1)模型研究发现,GM(1,1)模型只能得到原始数据的整体变化趋势,对于数据的波动性变化则没有显现,因此利用Markov链的相关理论对其进行补充是十分必要的。Markov链理论是基于概率统计的理论,适用于具有随机变化的动态过程,通过状态转移矩阵可以得到系统在下一个时刻所处状态的概率,因此将两者结合起来可以得到更加准确的预测结果。利用灰色-Markov模型进行挖掘比单纯使用灰色G(1,1)模型预测一个值的结果要更加合理,本模型由于在灰色模型的基础上使用了Markov知识,比灰色GM(1,1)模型的应用范围要广,总体效果要优于灰色GM(1,1)模型。
本文所提出的基于灰色-Markov模型的动态关联规则趋势度挖掘方法的重点是对灰色-Markov模型的运用。在描述算法之前将算法中所用到的名词进行解释,FP-Growth算法:文献[16]提出的一种经典的关联规则的挖掘方法;ITS算法:文献[4]提出的一种动态关联规则的挖掘算法;DRI:Definition of Rule Index,趋势度阈值;SRI:Support of Rule Index,趋势度[8]。下面将本文所提出方法的具体过程以及建模的过程进行详细描述:
(1)调用FP-Growth算法挖掘出满足支持度阈值的频繁项集。
(2)再次扫描数据库,得到每个频繁项集的支持度计数。
(3)根据支持度向量的变化趋势以及支持度向量的分类计算各频繁项集的趋势度SRI。
(4)判断各频繁项集的SRI是否大于趋势度阈值DRI。
(5)将不满足DRI要求的频繁项集的支持度计数序列用GM(1,1)模型进行建模,从而得到原始数据的预测公式。
(6)由预测公式得到原始数据的拟合值,进一步得到残差和残差百分比。运用Markov链分析方法,结合实际情况进行状态划分。
(7)计算每一个状态转移到其他任何状态的转移概率pij,进而得到一步转移概率矩阵 p和k步转移概率矩阵 p(k)。
(8)通过一步转移概率矩阵预测下一状态,通过k步转移概率矩阵预测当前状态下一状态开始的第k个状态,通过预测便可得知此支持度向量下一个或第k个值的取值的概率。
(9)确定预测对象未来的状态转移后,即确定了预测值的变动灰色区间,取灰区间的中值作为最终的预测的支持度计数。
(10)将预测得到的支持度计数加入原频繁项集支持度向量,判断新的支持度序列是否满足支持度阈值要求。
(11)判断(10)中满足支持度阈值的支持度序列的趋势度是否大于DRI。
(12)将(4)和(11)中满足要求的规则作为强趋势度动态关联规则进行输出。
算法流程图如图1所示。

图1 算法流程图
5 实例分析
实验数据采用SQL Server 2005自带的某商场2004年的销售数据作为实验数据。挖掘出形如{I1,I2}频繁项集,其含义为消费者购买I1产品之后购买I2产品在2004年每个月的支持度计数,其中I1、I2为商品的编号。设最小支持度为0.4,最小支持度数为40,最小置信度为0.4,趋势度阈值DRI=0.55。
实例分析过程:
第一步 调用FP-Growth算法进行挖掘,得到频繁项集:{I1,I2},{I2,I4},{I2,I5},{I4,I5}。
第二步 扫描数据库,得到各频繁项集支持度向量SV。SV{I1,I2}=[41,40,42,41,43,44,40,41] ;SV{I2,I4}=[37,39,40,40,41,42,43,45];SV{I2,I5}=[43,39,39,42,40,43,42,40];SV{I4,I5}=[43,38,38,42,41,39,42,40]。
第三步 根据趋势度的定义[8],计算各频繁项集的趋势度。{I1,I2}支持度向量中每个元素的支持度均大于最小支持度阈值,它属于支持度稳定型向量,SRI(I2,I4)=1;{I2,I4}支持度向量属于支持度上升型频繁向量,SRI(I2,I4)=1;{I2,I5}最大上升子时间序列长度为4,最大下降子时间序列向量长度为4,可得:SRI(I2,I5)=0.5 ;{I4,I5}最大上升子时间序列长度和最大下降子时间序列向量长度均为4,可得:SRI(I4,I5)=0.5。
第四步 根据趋势度阈值{I1,I2}和{I2,I4}为强动态关联规则,{I2,I5}和{I4,I5}为非强动态关联规则。
第五步 对非强动态关联规则{I2,I5}和{I4,I5}的支持度向量,运用GM(1,1)模型进行建模。
对规则{I2,I5}和{I4,I5}的支持度序列[43,39,39,42,40,43,42,40]和[43,38,38,42,41,39,42,40]分别作为原始序列:{x(0)=(x(0)(1),x(0)(2),…,x(0)(n)),n=1,2,…,8}和 {y(0)=(y(0)(1),y(0)(2),…,y(0)(n)),n=1,2,…,8} 。按以下步骤进行:
(1)首先根据公式(11)获得级比序列。经检验级比σ(k)满足:
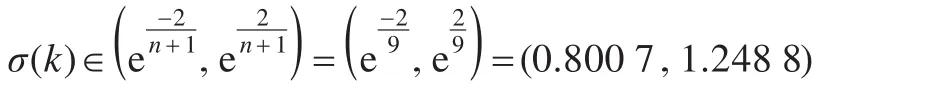
(2)不再对原序列进行预处理,直接对原始序列{x(0)=(x(0)(1),x(0)(2),…,x(0)(n)),n=1,2,…,8}建立 GM(1,1)模型。分别得到两个参数:a1=-0.008 618,b1=39.127 803;a2=-0.009 673,b2=38.245 032。根据表1可知,可以运用GM(1,1)模型对其进行中短期预测,分别得到两序列的时间影响方程:

第六步 利用时间影响方程得到模拟序列,分析规则{I2,I5}和{I4,I5}支持度的模拟值、残差和残差百分比,如表2所示。

表2 模拟值分析表
通过计算表中数据可知:序列x(1)的变化趋势是逐步减小的,根据这个灰色预测曲线方程得到的模拟值序列x的平均相对误差为2.54%,而年度最大误差为4.51%;序列y(1)的变化趋势是逐步增大的,根据这个灰色预测曲线方程得到的模拟值序列y(1)的平均相对误差为2.87%,而年度最大误差为5.71%,故此灰色模型预测的结果是可以接受的。
根据规则的支持度计数拟合结果和残差百分比划分出五种状态:E1、E2、E3、E4和E5。残差百分比小于 -8%设为E1;残差百分比大于 -8%且小于 -2%设为E2;残差百分比大于 -2%且小于2%设为E3;残差百分比大于2%且小于8%设为E4;残差百分比大于8%设为E5。
第七步 计算状态转移概率,确定状态转移矩阵。由上分析可知,规则{I2,I5},{I4,I5}各状态转移情况如表3所示。

表3 状态转移表
进一步得到一步状态转移概率矩阵和两步状态转移概率矩阵:
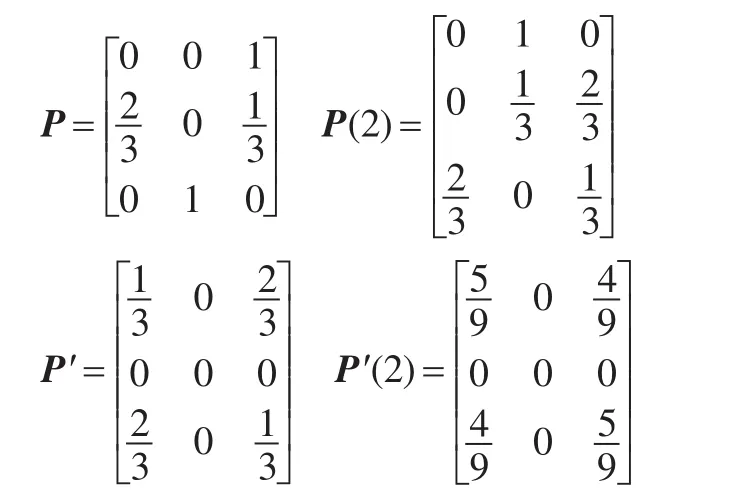
第八步 确定接下来两个月支持度计数的状态。规则{I2,I5}在第8个月处于状态E2,根据一步状态转移矩阵 P和两步状态转移矩阵 P(2),可知规则{I2,I5}在接下来两个月支持度计数分别处于E4和E2;规则{I4,I5}在第8个月处于状态E2,根据一步状态转移矩阵P′和两步状态转移矩阵 P′(2),可知规则{I4,I5}在接下来两个月支持度计数都将处于状态E4。
第九步 分别预测两规则在接下来两个月的值。得到规则{I2,I5}和{I4,I5}接下来两个月的支持度计数如表4所示。
第十步 将预测值添加到原规则支持度序列中。加入预测值后两规则的支持度向量分别为:


表4 支持度预测
第十一步 对预测之后的规则支持度向量再次计算趋势度。{I2,I5}最大上升子时间支持度序列长度为5,最大下降子时间支持度序列长度为4,根据公式(4)得:最大上升子时间支持度序列长度为6,最大下降子时间支持度序列长度为4,根据公式(4)得:SRI(I4,I5)=0.6 。
第十二步 生成规则阶段。分析规则{I1,I2}和{I2,I4},它的支持度和置信度都大于阈值,并且趋势度为1,因此它们都是强动态关联规则;频繁项集{I2,I5}的支持度和置信度都满足阈值要求,但是它的趋势度0.5<DRI=0.55,并且对支持度序列进行预测之后仍然小于趋势度阈值,因此它不是强动态关联规则;频繁项集{I4,I5}的支持度和置信度都满足阈值,且对其支持度序列进行预测之后满足阈值要求0.6>DRI=0.55,因此将{I4,I5}作为强动态关联规则输出。最终得到三组共6条高趋势度的动态 关 联 规 则 :I1⇒I2,I2⇒I1,I2⇒I4,I4⇒I2,I4⇒I5,I5⇒I4。
结果对比:
为了说明算法的有效性,本文用传统动态关联规则挖掘算法ITS算法[4]以及文献[8]中提出的基于趋势度的动态关联规则挖掘算法两种算法作对比,研究三种挖掘算法产生的规则。结果如表5所示。

表5 三种方法结果对比表
用传统的动态关联规则挖掘算法得到的强动态关联规则有8条,而用基于趋势度的动态关联规则挖掘算法可以得到4条高趋势度的动态关联规则,用本文所提出的方法可以得到6条高趋势度的动态关联规则。经过分析可知,规则I2⇒I5和I5⇒I2其支持度计数变化随机性比较大,决策者不能从中得到有效的决策信息;而对于规则I4⇒I5和I5⇒I4,研究其支持度向量序列可知,虽然现有的支持度计数变化随机性比较大,但是通过对支持度计数进行预测发现其支持度计数随机性在逐渐降低,可以从中得到有效的信息,所以将其作为强趋势度动态关联规则进行输出。因此,新的动态关联规则挖掘算法可以根据用户设定的趋势度阈值,针对动态关联规则中有一定变化趋势的规则进行挖掘,充分考虑到规则随时间而变化的特性,在一定程度上提高了规则挖掘的质量,同时也为决策者提供了更加全面、有效的信息,从而使决策更有依据、更可靠。
6 结语
本文在GM(1,1)模型和马尔科夫链理论相结合的基础上,将其组成的组合模型运用到动态关联规则趋势度的挖掘中。在动态关联规则趋势度的挖掘中运用本方法,不仅能直观了解到规则趋势度的总体的变化情况,还可以对其进行预测。结果表明本文方法能够在一定程度上提高规则挖掘的效率,为决策提供更可靠的信息。今后的主要研究方向将放在当原始数列波动性过大且无明显规律时如何保证预测的精度;对象为大数据库或者海量数据时,如何提高挖掘算法的效率和准确性[17]。
[1]Agrawal R,Imeielinksi T,Swami A.Mining association rules between sets of items in large databases[C]//Proceedings of the 1993 ACM SIGMOD Conference,1993:207-2l6.
[2]Au W H,Chan K C C.Mining changes in association rules:a fuzzy approach[J].Fuzzy Sets Syst,2005,149(1):87-104.
[3]荣冈,刘进锋,顾海杰.数据库中动态关联规则的挖掘[J].控制理论与应用,2007,24(1):129-133.
[4]沈斌,姚敏.一种新的动态关联规则及其挖掘算法[J].控制与决策,2009,24(9):1310-1315.
[5]Shen Bin,Yao Min,Wu Zhaohui,et al.Mining dynamic association rules with comments[J].Knowledge and Information Systems,2010,23(1):73-98.
[6]张忠林,许凡.基于小波变换的动态关联规则元规则挖掘方法[J].计算机应用,2012,32(7):1983-1986.
[7]刘俊,张忠林,谢彦峰,等.基于时间序列模型的动态关联规则元规则挖掘[J].计算机工程,2009(15):94-96.
[8]张忠林,曾庆飞,许凡.动态关联规则的趋势度挖掘方法[J].计算机应用,2012,32(1):196-198.
[9]Zhang Yi,Wei Yong,Zhou Ping.Improved approach of gray derivative in GM(1,1)model[J].The Journal of Grey System,2006,116(10):160-162.
[10]Sun Yanna.Optimization of grey derivative in GM(1,1)based on the discrete exponential sequence[C]//Proceedings of the 2nd International Symposium on Information Processing(ISTP2009),2009:313-315.
[11]Yang Jiangtian.Multivariable trend analysis using grey model for machinery condition monitoring[C]//Proceedings of the 11th World Congress in Mechanism and Machine Science,2004:2188-2191.
[12]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].北京:科学出版社,2004:142-146.
[13]刘思峰,邓聚龙.GM(1,1)模型的适用范围[J].系统工程理论及实践,2000,20(5):121-124.
[14]刘俊,谢彦峰,张忠林.基于灰色Markov模型动态关联规则元规则挖掘[J].计算机应用,2008,28(9):2353-2356.
[15]张忠林,刘俊,谢彦峰.AR-Markov模型在动态关联规则挖掘中的应用[J].计算机工程与应用,2010,46(14):135-137.
[16]Han J,Pei J,Yin Y.Mining frequent patterns without candidate generation[C]//Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data,Dallas,2000:1-12.
[17]Kuri-Morales A,Rodriguez-Erazo F.A search space reduction methodology for data mining in large databases[J].Engineering Applications of Artificial Intelligence,2009,22(1):57-65.

