运用Voellmy模型方法模拟泥石流运动堆积动力过程

陈 伟

(广东省环境地质勘查院，广东 广州 510000)

0 引言

泥石流灾害属于山区的一种突发性灾害，具有流速快、携带固体物质能量强和破坏力大等特点，是我国主要地质灾害类型之一(谢洪等，2006)。开展泥石流危险范围的预测工作具有重要的现实意义。

利用新一代的地理信息系统(GIS)，结合适用于泥石流两相流体分析的理论模型，综合地质、数值计算以及计算机科学等不同学科，对泥石流运动以及堆积过程进行模拟，进而为后期泥石流危险性评价区划及防治提供关键参数，是当前泥石流理论研究以及工程防治设计的研究热点和难点。从目前国内外泥石流运动堆积过程研究现状出发，探讨Voellmy连续介质模型原理以及GIS在泥石流研究中的应用，并以典型泥石流沟为例，通过模拟泥石流运动、堆积的动力过程，获取了泥石流体的最大速度、压力、过流量、堆积高度以及堆积面积等关键参数。

根据对国内外文献的分析，目前对泥石流堆积扇运动及堆积预测通常采用3种方法：经验统计方法、物理模拟方法、动力模型分析。

日本是较早也是较多研究泥石流运动及堆积预测的国家之一。池谷浩等1979年根据流域面积推算泥石流冲出量，根据冲出量推算泥石流堆积长度和堆积宽度，率先从统计学角度探讨了这一问题(池谷浩，1996);石川芳治(1999)研究了用模型实验模拟堆积区具有沟槽和隆起等微地貌时，泥石流堆积范围应如何修正以及泥石流体中细粒物质对泥石流堆积扩散的影响等。

欧美国家也很重视泥石流危险范围的研究。奥地利很早就进行了泥石流危险范围的预测工作，并引用交通信号中的红、黄、蓝3色的特定含义，将泥石流危险区分为3类(Blaikie et al，1994);Brien等开发了水力模型，模拟泥石流和流域内的堆积区;Ghilardi等(2001)开发了1个数学模型，考虑了侵蚀和堆积过程，以及不同类型的堆积物;Pasuto等(2004)采用多学科方法，从历史、地形地貌、地质结构、气象、土壤和森林管理等角度，对泥石流进行了评价。

唐川等(1992)应用泥石流堆积模型实验，将实验结果用多元回归曲线拟合，得到泥石流堆积形态函数与泥石流参数关系表达式;吴积善等(1993)根据泥石流典型地区(主要是东川小江流域)的资料，建立了泥石流最大堆积面积、最大堆积长度、最大堆积宽度和泥石流堆积幅角与流域面积、松散固体物质储量、主沟长度和流域最大相对高差的相关式。

利用动力模型进行泥石流运动及堆积预测是目前研究的热点，该模型通常采用数值方法，利用能量与运动转换法则对泥石流运移及堆积过程进行模拟。动力模型包括离散元模型、质量集中模型以及连续单元模型。其中，连续介质模型是建立在流体力学之上，利用物质－运动－能量消散的转换方程来描述泥石流的动力过程。因此，连续介质模型可以更为合理地刻画出泥石流固体物质的运动特性，从而被广泛使用(Hungr et al，1984)。

1 连续介质模型在泥石流中的应用

在连续介质模型中，泥石流流体被假设为一种非稳定以及非均质的流体，可以被2个主要流体参数来刻画(Hungr et al，2009)，即流体高度H(x，y，t)，m;平均流速U(x，y，t)，m/s：

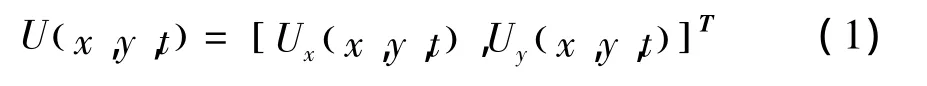
式(1)中，Ux为X方向的速度;Uy为Y方向的速度;T为平均速度的转置矩阵。速度大小可以被定义为：

式(2)中，‖U‖表示对速度U取绝对平均值，这就确保U在向量空间中为严格的正速度，流体速度的方向可以用单位向量(nU)来定义：

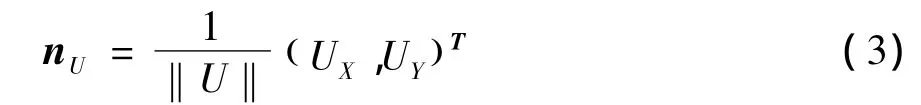
Voellmy流变模型用下列质量平衡公式来表达：

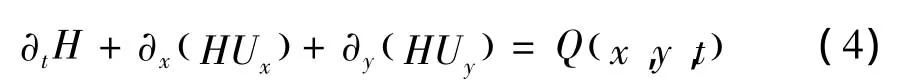
式(4)中，H为流体高度，m;Q x，y，()t，kg/(m2·s)为质量源，当Q=0时，表示没有物质沉积。在X和Y方向上，流体平均深度平衡方程可以分别表示为：

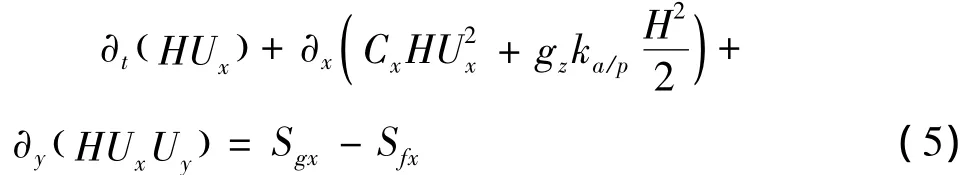
以及：

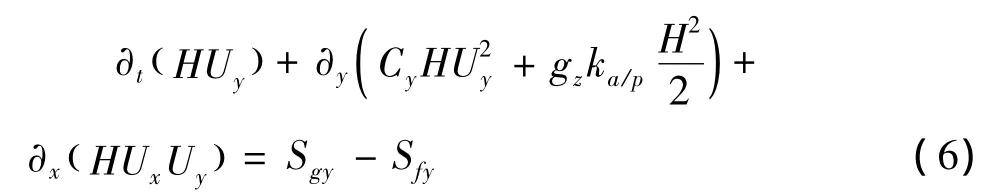
式(5)、(6)中，Cx以及Cy为剖面系数，gz为垂直方向的重力加速度。在Voellmy模型中，垂直方向的接触关系可以定义为非均质的摩尔－库伦关系。ka/p为土压力系数，可以用下列关系式来表示：

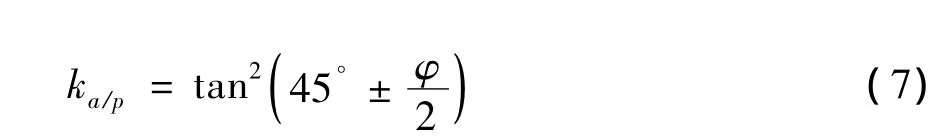
式(7)中，φ为泥石流流体的内摩擦角。

通过以上各式，可以得出Voellmy流变公式：

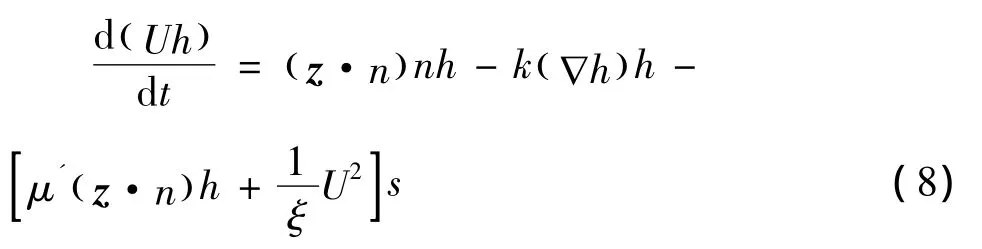
2 实例研究

2.1 泥石流沟基本特征

选取地震灾区汶川县某典型泥石流沟作为实例研究，该沟位于岷江右岸，流域面积5.8 km2，主沟长约5.2 km，以“V”型谷为主，流域海拔范围1 320～3 340 m之间，高差 1 020 m，主沟纵比降为200‰。该沟流域内出露基岩主要以花岗岩、板岩及千枚岩为主。沟道两岸多基岩出露，坡度较陡，平均坡度约40°～60°。该沟主要威胁到下游的阿坝师专、村庄、公路及农田等承灾体。通过对该沟流域的调查特征分析，可将该沟可分为清水、物源、流通及堆积4个区，各分区特征见表1。

表1 泥石流流域分区特征表Table 1 Zonation features of the debris flow basins

通过实地调查，该沟于1958年及1979年8月13日分别暴发中—大规模泥石流。其中1979年发生的泥石流持续时间约lh，速度较快，“龙头”高度为2.0～3.1 m，泥浆飞溅，泥位高度约3.1 m(康景文等，2011)。在“5·12”汶川特大地震的强大作用力之下，沟内及两岸松散固体物质激增，在强降雨或绵雨条件下，很容易暴发严重的泥石流灾害。

2.2 泥石流特征值计算

根据相关计算公式，分别计算出该沟全流域的暴雨历时、设计暴雨量、径流深度、设计洪水总量、概化矩形历时等参数，该沟的洪水总量、泥石流峰值流量、1次泥石流总量、1次泥石流冲出的固体物质总量等计算结果(表2、表3、表4、表5)。

表2 暴雨洪水流量计算结果Table 2 Calculation of rainstorm and flood flow

表3 泥石流峰值流量计算结果Table 3 Calculation of peak flow of debris flow

表4 1次泥石流总量计算结果Table 4 Calculation of the total amount of one-time debris flow

表5 1次泥石流固体物质总量计算表Table 5 Calculation of the total solid material of one-time debris flow

根据计算结果，该沟20年、50年及100年一遇的泥石流总量约4 230～9 052 m3。

2.3 泥石流运动及堆积数值模型建立

数字地面模型是泥石流数值模拟最基础，也是最重要的步骤，这直接决定了模拟结果的精度以及正确性。通过对工作区纸质地图进行矢量化后，利用ArcGIS软件，建立TIN(Triangulated Irregular Network)最优化不规则三角网模型，通过对TIN模型数字高程点的采集，获取模型网格点数字高程，并进行内插计算，最终获得研究区DEM。通过GIS模拟系统内置分析代码，获取流体的流速、高度、过流量等关键参数，并将计算所得的结果以GIS格式数据的形式以3D效果进行展示。

在上述连续介质模型原理的基础上，采用动力数值模拟计算软件，对该泥石流沟进行实例研究。模型长度=7 300 m，宽度=5 040 m，共计50 034个节点，49 580个单元。对该沟百年一遇的泥石流影响范围进行预测，1次泥石流固体物质总量为9 052 m3，建立的三维模型如图1所示。

图1 泥石流数值模拟三维模型Fig.1 3D numerical simulation model of debris flow

3 结果与讨论

采用常规的泥石流流量过程概化线和洪峰流量进行模拟，针对泥石流的堆积范围进行模拟，并为后期的危险性评价及区划提供技术支撑。通过模拟计算，泥石流最大速度、最大压力、过流量以及流体堆积高度、堆积特征如图2、图3、图4、图5、表6所示。

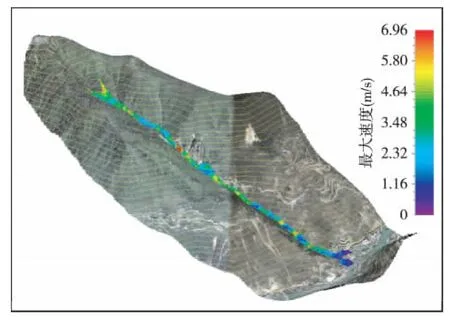
图2 泥石流最大速度特征图Fig.2 Characteristic diagram of maximum velocity of debris flow

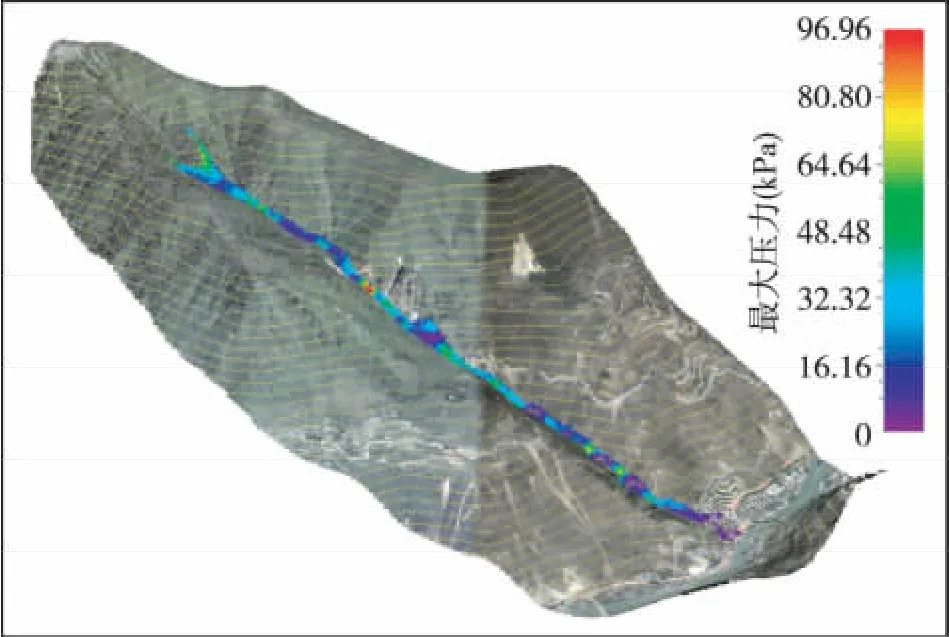
图3 泥石流最大压力特征图Fig.3 Characteristic diagram of maximum pressure of debris flow

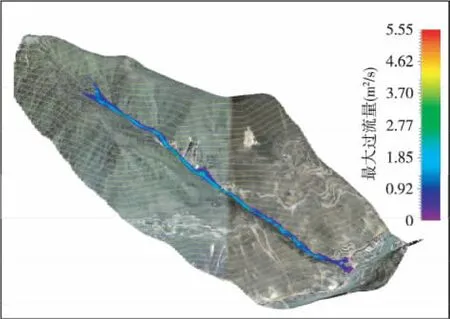
图4 泥石流最大过流量特征图Fig.4 Characteristic diagram of maximum momentum of debris flow

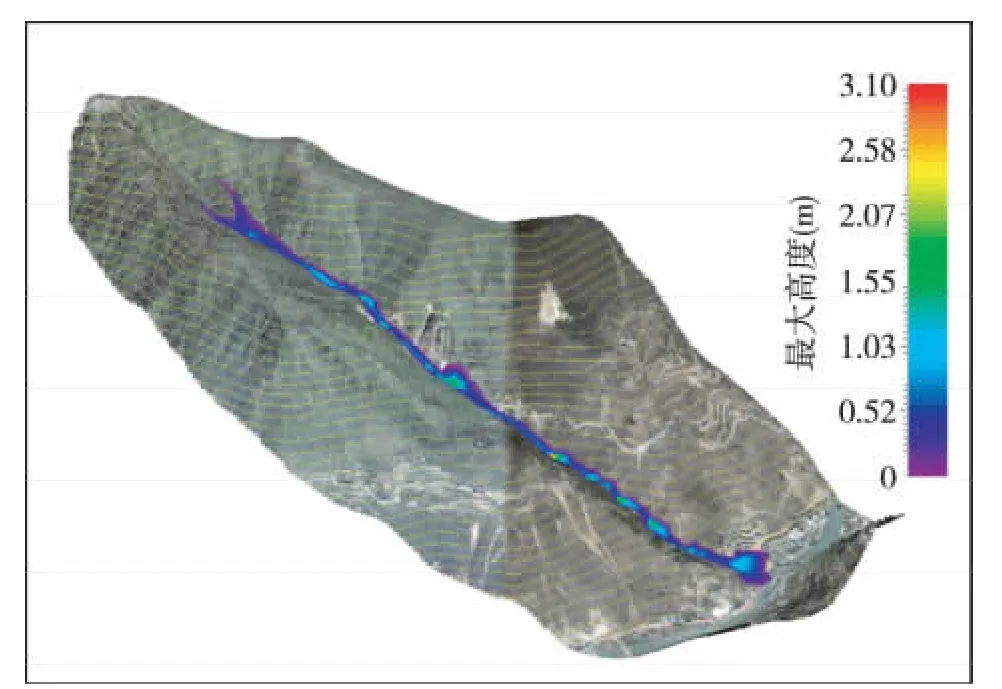
图5 泥石流最大流体堆积高度特征图Fig.5 Characteristic diagram of maximum accumulation height of debris flow

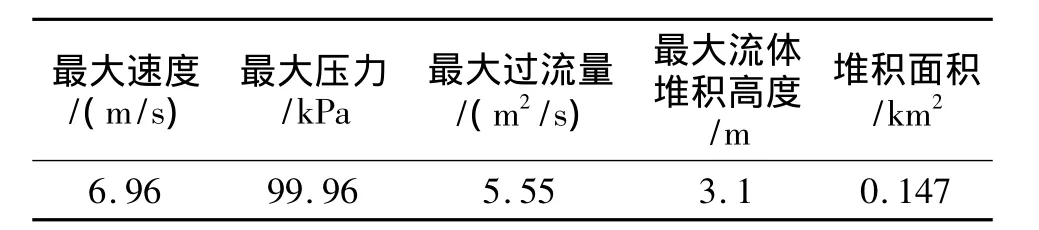
表6 泥石流运动及堆积计算表Table 6 Calculation of the movement and accumulation of debris flow

从以上分析结果图可以看出，该沟泥石流暴发后，在泥石流的流通区和物源区，泥石流流体的最大流速可以达到6.96 m/s，快速的泥石流流体可以产生很强的侧蚀和底蚀作用，加大了泥石流流体的固体物质携带能力，并大幅度地增加了固体物质运移距离，表现出强烈的侵蚀作用。在沟谷的中下段，特别是出山口至主河之间的沟段，泥石流流速已经有大幅度的降低，以沉积作用为主。根据数值模拟计算结果，在1次泥石流固体物质总量为9 052 m3的情况下，泥石流流体携带固体物质冲出沟口后，堆积扇面积可高达0.147 km2，将对沟口大量居民、民房、公路等造成严重危害。

另外，根据模拟，泥石流的堆积扇扇顶刚好冲入岷江，对岷江主河道造成挤迫，虽未完全阻断，但会造成河流的回水，对位于沟口所处的岷江上游区段造成潜在威胁。

4 结论

(1)泥石流危险范围预测是泥石流危险性评价及区划的一项重要研究内容，特别是针对地震灾区泥石流灾害防治有着重要的意义。

(2)在预测泥石流危险范围时，动力模型分析方法有着经验统计方法以及物理模拟等方法不具备的优势，可以更为合理地刻画出泥石流固体物质的运动特性，从而被广泛使用。

(3)选取地震灾区汶川县某典型泥石流沟作为实例研究，该沟流域面积5.8 km2，主沟长约5.2 km，该沟20年、50年及100年一遇的泥石流总量约为4 230～9 052 m3。

(4)采用动力数值模拟计算软件，建立泥石流沟的数值模型，对该沟百年一遇的泥石流影响范围进行预测，计算结果显示该沟在1次泥石流固体物质总量为9 052 m3的情况下，最大速度为6.96 m/s，最大压力99.96 kPa，最大过流量为5.55 m2/s，最大流体堆积高度为3.1 m，堆积面积为0.147 km2。不仅对下游居民造成严重威胁，还有可能阻塞岷江主河道。

(5)根据野外调查情况，并结合数值模拟研究，证明基于GIS技术平台以及Voellmy连续介质模型可以很好地模拟泥石流运动、堆积的动力过程，在泥石流危险范围预测工作中具有较高的准确性。

池谷浩.1996.云仙水无川泥砂流失量的推算方法［J］.水土保持科技情报，(4)：30－34.

康景文，黄建波，周勇，等.2011.汶川县威州镇羊岭沟泥石流特征及成因分析［J］.施工技术，40(增刊)：180－184.

唐川，刘希林.1992.泥石流动力堆积模拟和危险范围预测模型［M］.北京：科学出版社.

谢洪，钟敦伦，韦方强，等.2006.我国山区城镇泥石流灾害及其成因［J］.山地学报，24(1)：79－87.

吴积善，田连权，康志诚，等.1993.泥石流及其综合治理［M］.北京：科学出版社.

石川芳治.1999.地震にょる土石流の発生に係わる地形，地质条件［J］.砂防学会誌，51(5)：35－42.

BLAIKIE P，CANNON T.1994.At Risk：Natural Hazards，Peoples Vulnerability and Disasters［M］.London，UK：Psychology Press.

GHILARDI P，NATALE L，SAVI F.2001.Modelling debris－flow propagation and deposition［J］.Physics and Chemistry of the Earth：Part C，26(9)：651 －656.

HUNGR O，MORGAN G C，KELLERHALS R.1984.Quantitative analysis of debris torrent hazards for design of remedial measures［J］.Canadian Geotechnical Journal，21(4)：663－677.

HUNGR O，MCDOUGALL S.2009.Two numerical models for landslide dynamic analysis［J］.Computers ＆ Geosciences，35(5)：978－992.

JULIEN P Y，O'BRIEN J S.1997.Slected notes on debris flow dynamics［J］.Lecture Notes in Earth Sciences，64：144 －162.

PASUTO A，SOLDATI M.2004.An integrated approach for hazard assessment and mitigation of debris lows in the Italian Dolomites［J］.Geomorphology，61(1/2)：59 － 70.