基于模糊聚类分析的城市综合竞争力聚类

付云鹏，马树才

(辽宁大学经济学院,辽宁 沈阳,110036)



基于模糊聚类分析的城市综合竞争力聚类

付云鹏，马树才

(辽宁大学经济学院,辽宁 沈阳,110036)

构建了城市综合经济实力、城市基础设施建设、社会公共设施建设和城市资源环境建设共4个维度的综合评价指标体系，利用模糊聚类分析方法对我国15个副省级城市的城市综合竞争力进行聚类分析。

副省级城市；综合竞争力；模糊聚类分析；指标体系

城市竞争力是一个城市所具有的由各种发展要素综合形成的整体实力的综合体现，是在社会、经济结构、价值观念、文化、制度政策等多个因素综合作用下创造和维持的，是城市为其自身发展在区域内进行资源优化配置的能力。城市竞争力是国家、地区间竞争力的基础，国家、地区间的竞争在一定程度上表现为城市之间的竞争。城市竞争力问题早已成为当今时代研究和关注的焦点。对城市竞争力最早的研究源于世界经济论坛与瑞士洛桑国际管理学院提出的竞争力评估模型。近年来，我国学者也对城市竞争力方面的研究进行了完善和发展。国内学者对城市竞争力的研究大多集中于不同城市之间综合竞争力的比较和排序方面。常用的方法包括：第一，因子分析法。郭利平等[1]、朱红根等[2]、陈晓林[3]、曾鹏等[4]、于丽英等[5]、杨晓楠[6]、孙霞[7]、李晓菲[8]等分别通过构建城市综合竞争能力评价指标体系，利用因子分析法对西部9省会大城市、江西省各城市、江苏省各城市、桂林中心城市、长三角城市、武汉城市群、浙江省11个城市和我国35个城市的城市综合竞争力进行了排序。第二，隶属函数法。陈志[9,10]、刘耀彬[11]利用梯形模糊隶属度函数来表示指标的属性值，采用线性加权函数评价各城市综合竞争力，对不同城市的综合竞争力进行比较分析。第三，空间计量方法。董春等[12]从经济发展竞争力、社会发展竞争力和环境发展竞争力共3个方面，将空间统计分析与GIS相结合对中国284个地级以上城市的综合竞争力进行了评价分析。张振华等[13]利用熵权灰色关联投影模型对中国各地区的投资环境竞争力进行了排名。陈雯[14]将基于模糊等价关系和模糊C均值聚类两种方法结合起来，以2005年为样本点，分别对中国15个副省级城市和武汉城市圈的城市综合竞争力进行了聚类分析。笔者在前人研究成果的基础上，通过从城市综合经济实力、城市基础设施建设、社会公共设施建设和城市资源环境建设共4个方面构建指标体系，利用模糊聚类分析法对中国15所副省级城市的城市综合竞争力进行聚类分析。

1 模糊聚类分析

模糊聚类是采用模糊数学方法，依据客观事物间的特征、亲疏程度和相似性，通过建立模糊相似关系对客观事物进行分类的一门多元聚类方法。模糊聚类分析方法是一种很有效的聚类方法，通过构造模糊相似关系，然后进行模糊传递闭包，根据模糊传递闭包矩阵，按λ截集矩阵进行动态聚类，具体步骤如下：

1.1 数据标准化

由于指标数据的量纲不同，无法直接进行比较，所以必须先对指标数据进行无量纲处理。设样本集合X={x1,xn,…,xn}，用xij(i=1,2,…,n;j=1,2,…,m)表示每个样本的指标值，n为样本容量，m为指标的个数。笔者选取的指标体系中的指标均为正向指标，可用半升梯形模糊隶属函数将原始数据进行标准化处理，即

(2)

其中mij和Mij分别为第i样本第j个指标数据的最小值和最大值。yij的值在[0,1]之间，表示指标的隶属度函数值，其值越大表明其指标数据越接近于最大值。

1.2 构建模糊相似矩阵

构造模糊相似矩阵的关键就是确定其相似系数rij，rij表示xi与xj的相似程度，笔者采用绝对值减数法[15]来确定相似系数，即

其中c∈(0,1)，通过适当选取c值使rij∈[0,1]，从而得到模糊相似矩阵R。

1.3 计算模糊传递闭包

利用平方自合成方法求模糊传递闭包t(R)，即

R2⟹R4⟹…⟹R2k=t(R)

其中k≤log2n+1。

1.4 聚类

适当选取置信水平值λ∈[0,1]，求t(R)的λ截距阵t(R)λ，按t(R)λ进行分类，所得分类就是λ水平上的等价分类。

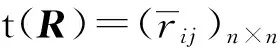
3 实证分析

选取中国15个副省级城市沈阳、大连、长春、哈尔滨、南京、杭州、宁波、厦门、济南、青岛、武汉、广州、深圳、成都和西安作为研究对象，对城市的综合竞争力进行聚类分析。从城市综合经济实力、城市基础设施建设、社会公共设施建设和城市资源环境建设共4个维度来探讨城市的综合竞争力。遵循科学性、可行性、整体性和可比性原则构建指标体系(表1)。

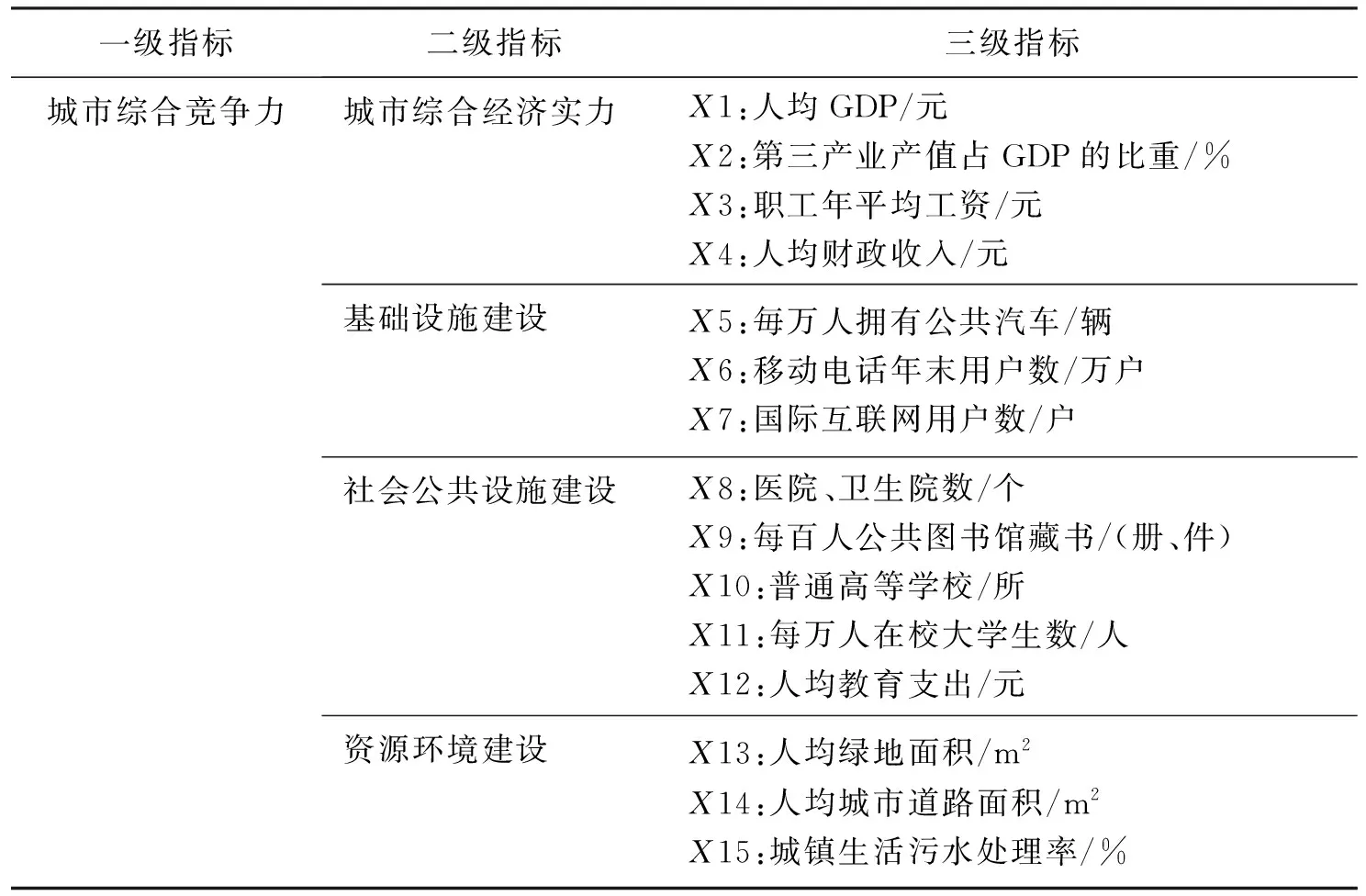
表1 城市综合竞争力评价指标体系

根据《中国城市统计年鉴2011》查得表1中各指标数据的值，对于年鉴中没有的直接给出的指标数据可通过简单的计算求得。由于本次研究选取15所城市进行聚类，所以所得矩阵为15阶矩阵，计算量较大，因此本次研究采用Matlab 7.0软件编程求解，具体程序如下：

I=ones(15, 15) ; %8阶单位阵

for i=1:15

for j= 1:15

Y(i,j)=(abs(X(i,1)-X(j,1))+abs(X(i,2)-X(j,2))+abs(X(i,3)-X(j,3))+abs(X(i,4)-

X(j,4))+abs(X(i,5)-X(j,5))+abs(X(i,6)-X(j,6))+abs(X(i,7)-X(j,7))+abs(X(i,8)-

X(j,8))+abs(X(i,9)-X(j,9)) +abs(X(i,10)-X(j,10)) +abs(X(i,11)-X(j,11))+abs(X(i,12)-X(j,12))+abs(X(i,13)-X(j,13)) +abs(X(i,14)-X(j,14)) +abs(X(i,15)-X(j,15))) ;

end

end

R=round((I-(1/15)*Y)*100)/100

步骤2：计算传递闭包。

for j=1:15

for i=1:15

y(i,j)=0;

for k=1:15

mn(k)=min(R(i,k),R(k,j));

end

y(i,j)=max(mn);

end

end

y

tr(R)=y

步骤3：聚类。

L=[1,0.9,0.89,0.88,0.87,0.85,0.83,0.81,0.74,0.47];

for k=L

for i=1: 8

for j=1: 8

if y(i,j)>=k

RK(i,j)=1;

else

RK(i,j)=0;

end

end

end

RK

聚类

将t(R)中元素进行排序为

1>0.9>0.89>0.88>0.87>0.85>0.83>0.81>0.74>0.47。

取置信水平λ=1，此时X中的元素被分为15类：

{x1},{x2},{x3},{x4},{x5},{x6},{x7},{x8},{x9},{x10},{x11},{x12},{x13},{x14},{x15}；

{x1},{x2},{x3},{x4,x15},{x5},{x6},{x7},{x8},{x9},{x10},{x11},{x12},{x13},{x14}；

取置信水平λ=0.89时，得相似类为

{x3},{x4,x15,x14,x2,x1},{x5},{x6},{x7},{x8},{x9},{x10},{x11},{x12},{x13},{x14}；

取置信水平λ=0.88时，得相似类为

{x3},{x4,x15,x14,x2,x1,x7},{x5},{x6},{x8},{x9},{x10},{x11},{x12},{x13},{x14}；

取置信水平λ=0.87时，得相似类为

{x3},{x4,x15,x14,x2,x1,x7,x6,x10},{x5},{x8},{x9},{x11},{x12},{x13},{x14}；

取置信水平λ=0.85时，得相似类为

{x4,x15,x14,x2,x1,x7,x6,x10,x3,x9,x11},{x5},{x8},{x12},{x13},{x14}；

取置信水平λ=0.83时，得相似类为

{x4,x15,x14,x2,x1,x7,x6,x10,x3,x9,x11,x14,x8},{x5},{x12},{x13}；

取置信水平λ=0.81时，得相似类为

{x4,x15,x14,x2,x1,x7,x6,x10,x3,x9,x11,x14,x8,x5},{x12},{x13}；

取置信水平λ=0.74时，得相似类为

{x4,x15,x14,x2,x1,x7,x6,x10,x3,x9,x11,x14,x8,x5,x12},{x13}；

取置信水平λ=0.47时，得相似类为

{x4,x15,x14,x2,x1,x7,x6,x10,x3,x9,x11,x14,x8,x5,x12,x13}。

动态聚类图为

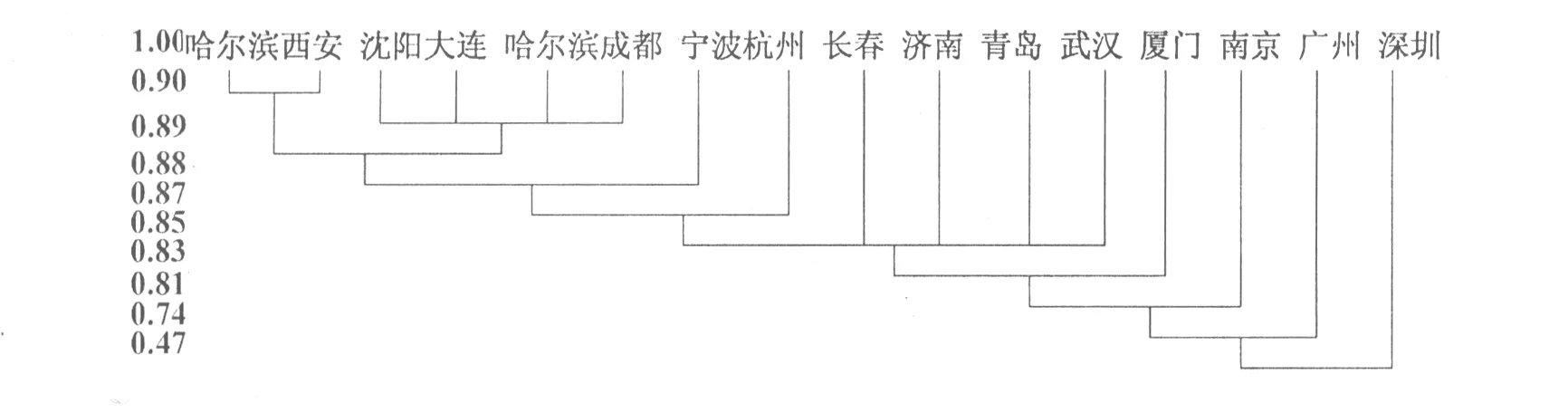
图1 城市综合竞争力动态聚类结果

4 结 论

通过从城市综合经济实力、城市基础设施建设、社会公共设施建设和城市资源环境建设共4个维度构建15个指标体系，采用模糊聚类分析法，利用Matlab 7.0软件编程求解模糊相似矩阵的传递闭包，进而对15个城市的综合竞争力进行动态聚类，得到不同截集水平下的不同分类情况。

[1] 郭利平,沈玉芳.西部9省会大城市综合竞争力的分析与研究[J].人文地理,2005(1):10-13.

[2] 朱红根,彭道宾.江西省各城市综合竞争力比较研究——因子分析法及其应用[J].江西农业大学学报:社会科学版,2005,4(2):51-53.

[3] 陈晓林.基于因子分析的江苏城市综合竞争力比较[J].经济研究导刊,2007(10):149-151.

[4] 曾鹏,蒋团标,覃顺梅.桂林中心城市综合竞争力评价及其诊断研究[J].统计与决策,2007(9):69-71.

[5] 于丽英,郭洪晶.城市协作框架下的长三角城市综合竞争力评价指标体系研究[J].科技管理研究,2010(11):95-98.

[6] 杨晓楠.武汉城市群城市竞争力研究分析[J].赤峰学院学报：自然科学版，2015，31(5下)：42-44.

[7] 孙霞.基于因子分析和聚类分析的城市竞争力综合评价——以浙江为例[J].赤峰学院学报：自然科学版，2013,29(11下)：53-55.

[8] 李晓菲.我国35个主要城市的综合发展水平研究[J].赤峰学院学报：自然科学版，2015,31(9下)：49-51.

[9] 陈志.中国15个副省级城市综合竞争力比较研究[J].特区经济,2006(11):33-35.

[10] 陈志.中国副省级城市综合竞争力评价与比较[J].商业研究,2007(6):13-17.

[11] 刘耀彬.中国副省级城市综合竞争力比较——兼论武汉城市综合竞争力的提升[J].湖北大学学报:哲学社会科学版,2007,34(2):57-60.

[12] 董春，王桂新，宋全红，等.中国地级及以上城市综合竞争力空间分布模式[J].辽宁工程技术大学学报:自然科学版,2009,28(3):359-362.

[13] 张振华,吉生保.中国各地区投资环境竞争力评价——基于熵权灰色关联投影模型的实证分析[J].中国物价,2012(4):49-52.

[14] 陈雯.模糊聚类在城市综合竞争力分类中的应用[J].武汉：华中师范大学，2008.

[15] 罗承忠.模糊集引论[M].北京:北京师范大学出版社,2005.

The City’s Comprehensive Competitiveness Cluster Based on Fuzzy Clustering Analysis

FU Yun-peng，MA Shu-cai
(School of Economics Liaoning University,Shenyang Liaoning，110136,China)

By building comprehensive evaluation index systems of the four dimensions including the city’s comprehensive economic strength, urban infrastructure construction, public facilities construction and urban resources and environment construction, this article analyzes the city’s comprehensive competitiveness of China’s 15 sub-provincial cities using fuzzy clustering analysis.

Sub-provincial cities; comprehensive competitiveness; fuzzy clustering; index system

国家社科基金青年项目(项目编号：13CRK027)；辽宁省教育科学“十二五”规划课题(课题编号:JG15DB141)；辽宁省教育厅科学研究一般项目 (项目编号:W2015171)。

2015-06-26

10.3969/J.ISSN.1672-7983.2015.03.013

O159

A

1672-7983(2015)03-0069-05

付云鹏(1978-)，女，副教授，博士。主要研究方向：模糊数学、计量经济模型及其应用。

(责任编辑：朱宝昌)