基于粒子群优化的PI预测函数励磁控制器

张鹏宙，倪家健，张钰，胡 华，蒋卫芳

(1．南京国电环保科技有限公司，江苏南京 210061;2．国电科学技术研究院，江苏南京 210031 3．江苏釜鼎能源科技有限公司，江苏南京 210009)

基于粒子群优化的PI预测函数励磁控制器

张鹏宙1，倪家健1，张钰2，胡 华3，蒋卫芳3

(1．南京国电环保科技有限公司，江苏南京 210061;2．国电科学技术研究院，江苏南京 210031 3．江苏釜鼎能源科技有限公司，江苏南京 210009)

将PI控制器与预测函数算法相结合，利用粒子群算法优化整定其参数，提出了一种新型的基于粒子群优化的PI预测函数励磁控制器的设计方法。该算法具有广义上的PI控制器的两个参数，同时具有预测函数算法对模型要求低和上升速度快等优点，同时利用粒子群算法优化PI参数，使其克服了传统PI控制器参数难以整定的缺点。仿真结果表明该算法不仅能有效的解决机端电压偏移问题，还能有效的抑制电网低频振荡，且具有较好的鲁棒性，同时PI参数整定方便，为电力系统稳定性控制提供了一种新型有效的方法。

粒子群;PI控制器;预测函数;励磁控制

大量的实践表明通过改进励磁控制规律可以提高电力系统的稳定性。目前常见的励磁控制规律主要有:PID、带电力系统稳定器(PSS)的PID、分数阶PID(FOPID)、预测控制和分数阶PID预测函数控制等［1－5］。本研究以预测函数控制算法为基础，利用PI控制算法去改进其最优性能指标，同时利用粒子群算法对其广义的PI参数进行整定，提出了一种基于粒子群优化的PI预测函数励磁控制器。

1 基于PI的预测函数算法

1．1 基本预测函数算法

预测函数控制［6－9］具有一般预测控制方法的基本原理。其与传统的预测控制方法最大的不同在于其控制量是一组预先选定的基函数的线性组合，这使其在线计算量减小，提高了响应速度。其基函数的选择与过程特性和拟跟踪设定值有关。PFC的控制输入被表示为一系列已知基函数线性组合，即:

式中:μ(k+i)表示在k+i时刻的控制量;μjk表示基函数的加权系数;fkj(i)表示基函数在t=iT时刻的取值;J表示基函数的阶数。

下式(2)为预测的P步参考轨迹:

式中:yr(k+i)为k+i时刻的参考轨迹;C(k)为k时刻的设定值;yp(k)为k时刻的过程实际输出值;α为柔化因子。预测函数的模型取其状态空间方程:

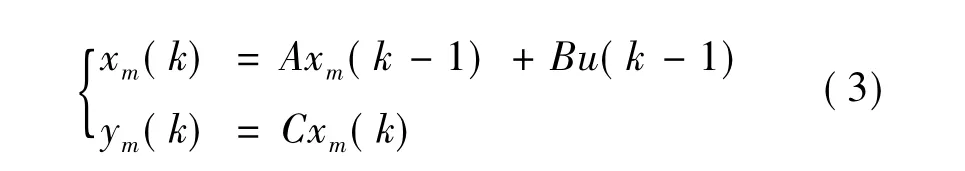
式中:ym(k)为k时刻模型预测输出;xm(k)为k时刻模型状态值;u(k－1)为k－1控制输入;A，B，C为矩阵方程系数。

由(3)式递推得到i时刻的预测输出为:

由(4)式并且结合模型输出与实际输出之间的误差，可得P步预测模型输出为:

由式(2)、(3)、(5)可得:

利用二次型目标函数D=‖Yp(k)－Ye(k)‖2，令，结合(1)式即可求得预测控制量。

1．2 基于PI的预测函数算法推导

利用PI算法对预测函数算法的目标函数进行改进，使推导的控制器具有广义上的比例(P)和积分(I)的结构特征。根据PI控制器的结构，以及传统的二次型目标函数，可得改进的PI目标函数为:

为了便于推导，将(7)改写为矩阵形式:

式(8)中，Q和R分别为误差加权矩阵和控制量加权矩阵，U(k)为控制量矩阵。

令:

式(6)表示为:

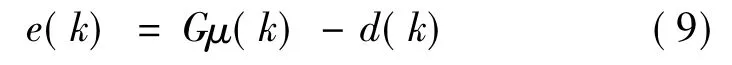
由式(9)推导可得:

引入移位算子，式(9)、(10)改写为:

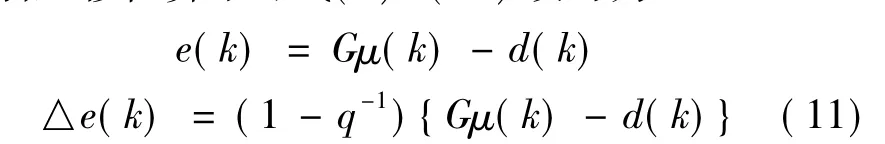
在式(8)中，控制量为:

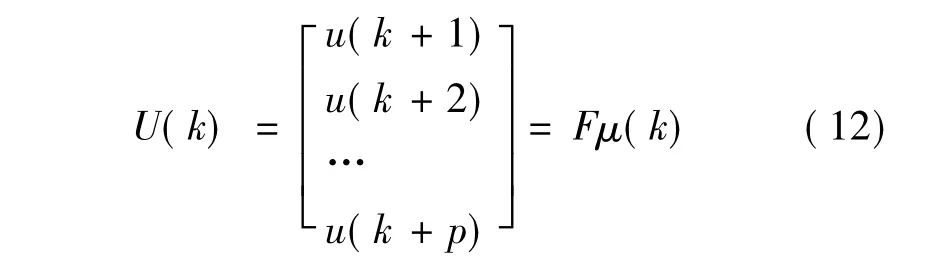
其中:K=Kp(1－q－1)2+Ki

2 基于粒子群算法整定PI预测函数算法

粒子群算法［10］采用“群体”和“进化”的概念，依据个体(粒子)的适应值进行进化。每个粒子根据自己和同伴的经验决定自己的速度和位置的更新，最终在全空间中搜索出最优解。

N维搜索空间中有m个粒子，设Xi=(xi1，xi2，…xiN)为粒子i(i=1，2，3…，m)的当前位置，Vi= (Vi1，Vi2，…，ViN)为微粒 i的当前飞行速度，Pi= (pi1，pi2，…，piN)为微粒i所经历的最优位置，相应的适应值称为个体的最优解pbesti，对于最小化问题，目标函数值越小，对应的适应值越好，为方便讨论，令f(X)为目标函数，则微粒i当前最好的位置为:

式中:t表示第t代。

群体中所有粒子经历过的最优位置pg(t):

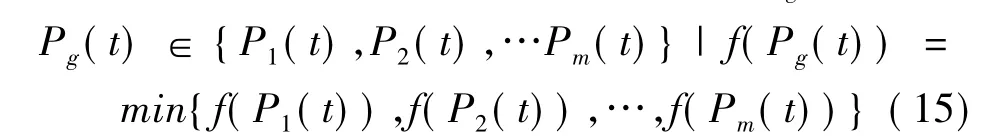
粒子根据下式更新自己的速度和位置:

式中:i=1，2，…，m;j=1，2，…，N;c1，c2为学习因子，非负常数，c1调节微粒飞向自身最好位置的步长，c2调节微粒飞向全局最好位置的步长，通常取c1=c2=2，r1，r2为介于(0～1)机数，群体规模m一般去20～40，ω为惯性因子，非负，ω值较小，则局部寻优能力强，全局寻优能力弱，ω值较大则反之，经试验发现，动态ω能获得比固定值更好的寻优效果，目前，采用较多的是Shi建议的线性减权值(linearly decreasing weight，LDW)策略，如式:

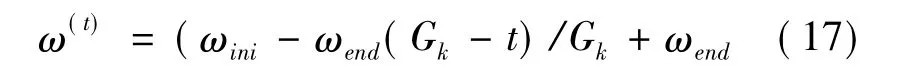
式中Gk为最大进化代数，ωini为初始惯性权值，ωend为迭代至最大代数时惯性权值。

改进的预测函数控制(PIPFC)具有两个参数即Kp，Ki，使调节更加灵活，但如果紧靠经验和实验获得，不仅费时，最终可能得不到最优的效果。粒子群具有算法简单、收敛速度快、可调参数少等优点，用粒子群调节PIPFC的两个参数，以期用最短时间获得最优的控制效果。若粒子数为m，则种群规模是的矩阵。

选择适应度

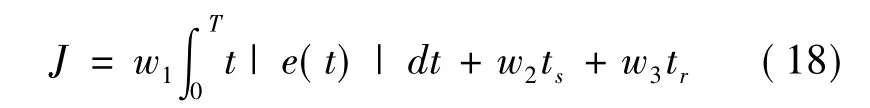
式中w1，w2，w3为权值;ts调节时间;tr上升时间。

算法步骤:种群初始化，包括种群数量，迭代次数，学习因子c1，c2，惯性因子ω，粒子的位置和速度;计算每个粒子的适应度，确定个体最优位置Pi(t)和群体最优位置Pg(t);按式(8)更新每个粒子的位置和速度;按式(6)、(7)更新个体最优值和群体最优值;迭代次数t加1，按式(9)更新ω;如果t大于最大迭代次数则执行步骤7否则回到步骤3;最终的Pg(t)为所得到的最优参数。

3 励磁控制系统

同步发电机的励磁系统可以看作是一个电压调节器，由其向同步发电机提供稳定的励磁［11］。在一般情况下，其动态模型由以下三个一阶环节构成:

放大环节有:

步电机环节:

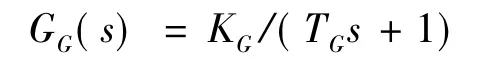
于检测滤波环节:

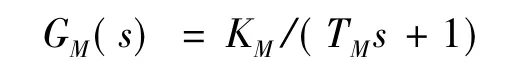
则同步发电机的励磁系统传递函数为:

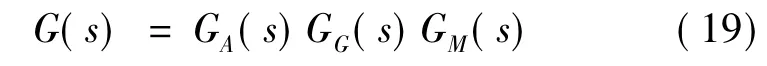
用粒子群优化PIPFC参数的控制框见如图1。

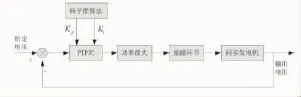
图1 控制系统的控制示意

4 仿真分析

首先通过PSO算法研究PIPFC参数的整定过程，PSO优化PIPFC参数设置为:微粒数m=60，维数dim=5，学习因子c1=c2=2，最大迭代次数Gk=60，惯性权值ωini=0．9，ωend=0．4，适应度权值w1=0．7，w2=0．6，w2=0．8。如图2所示，粒子群算法迭代23次左右，寻找到最优值，之后适应度保持不变，所以运用粒子群算法去优化PIPFC算法的参数可以起到比较好的控制效果。

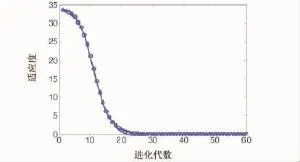
图2 进化代数与适应度的关系

接下去利用PSO算法优化所得的PIPFC控制器去控制同步电机的励磁，并且参考文献［6］与PFC算法和FOPIDPFC算法的参数，对比三种算法的控制效果见图3。

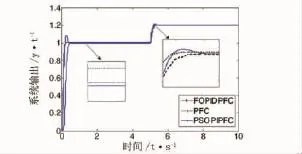
图3 五种算法启动和调压时系统输出响应曲线

图3 的0到5s的过程是发电机启动时的系统响应曲线，实线是PSOPIPFC的仿真曲线，划线是FOPIDPFC的仿真曲线，点线是PFC的仿真曲线。从图可知，在发电机启动时，PFC虽然上升速度较快，但是达到稳定后有较大的静态偏移;FOPIDPFC虽然稳定后静态偏移较小，但是达到静态的时间较长且超调较大;而发电机在PSOPFC的控制下，不仅达到稳定的时间较快，而且静态偏移最小，但缺点是PSOPIPFC控制下系统超调较大。

图3的5到10s是发电机在5s时受到一个调压扰动。系统在PFC控制下，再次过度到静态稳定时间较快，但是静态偏移越来越大，若是调压次数较多，则输出的电能质量将较差;在FOPIDPFC控制下，虽然静态误差小，但是达到静态的时间较长;而在PSOPIPFC的控制下，其达到静态的时间与PFC相近，静态误差比最小，所以在克服调压干扰时，PSOPIPFC的性能较好，但是超调较大。

图4 是发电机高压侧线路三相断路路时的输出响应曲线。从图中可以看出，PFC和FOPIDPFC的超调较大，对系统的绝缘要求较高，经济性较差。PFC过度不平滑且静态误差随扰动次数增加而变大。PSOPIPFC与它们相比超调最小，达到静态的时间是三者中最快的，并且静态误差几乎为零，是三者中控制效果最好的。

图5 是发电机高压侧线路三相短路时的输出响应曲线。从图中可以看出，PFC超调较大，同时PFC在调整的时过渡平滑性较差，对机械性能要求较高，FOPIDPFC调整过程平滑，但是稳态误差较大。而PSOPFC控制器，超调较小，达到静态稳定时间最短，而且整个过程很平滑，对机械的损伤最小。

5 结语

随着社会经济的发展，对电能质量的要求越来越高，常见的控制方法要么控制效果差，要么控制较为复杂，实现成本较高，所以需要一种实现较为简单，同时控制精度较高的控制策略。针对粒子群算法具有简单，收敛速度快等优点，提出了用PSO优化PI测函数控制参数的方法，并将结果与其余两种算法对比，结果表明基于PSO优化的PI预测函数励磁控制算法具有响应速度快，鲁棒性强的优点。值得提出的是，文中选取的被控对象是单输入单输出系统，对多变量系统尚待研究。

［1］陆继明，刘伯康，毛承雄，等．基于机电配置的线性最优励磁控制设计方法［J］．大电机技术，2009，(1):58－63．

［2］刘辉，李啸骢，韦化，等．基于目标状态方程的非线性预测励磁控制器的设计［J］．中国电机工程学报，2005，25(17):28－31．

［3］Giuseppe F，Mario R．Nonlinear control design for excitation controller and power system stabilizer［J］．Control Engineering Practice，2011，19(3):243－251．

［4］姚舜才，潘宏侠．粒子群优化同步电机分数阶鲁棒励磁控制器［J］．中国电机工程学报，2010，30(21):91－97．

［5］张秀华，张庆灵，靖新．具有鲁棒性分代数模型的励磁控制器模型［J］．电机与控制学报，2005，9(3):229－234．

［6］郭伟，倪家健，李涛，等．基于时域的分数阶PID预测函数励磁控制器［J］．仪器仪表学报，2012，32(11):2461－2467．

［7］Richalet J．Predictive Functonal control－application to fast and accurate robots［C］//Proc of the 10th IFAC World Congress．Oxford:Pergamon Press，1987:251－258．

［8］郭敬，赵克定，郭治富．液压仿真转台的PFC－PID串级控制［J］．航空学报，2008，29(5):1395－1400．

［9］夏泽中．张光明．预测函数控制及其在伺服系统中的仿真研究［J］．中国电机工程学报，2005，25(14):130－134．

［10］金丰，项福禄，天罡，等．主汽温串级控制系统PSO优化方法的工程实践［J］．现代电力，2010，27(4):78－82．

［11］IEEE Power Engineering Society．IEEE standard definition for excitation systems for synchronous machines IEEE std 421．1［S］．New York，NY，USA:Energy Development and Power Generation Committee，2007．

Improved PI predictive functional excitation controller based on PSO

It proposes a new design of excitation controller of PI prediction function，combining the algorithm of PI and the algorithm of Prediction Function，and tuning parameters based on PSO．The improved algorithm does not only have the two parameters of the PI controller in a broad sense，but also have the advantages of lower degree of precision to parametric models and rising fast，etc．，at the same time using PSO to tune two parameters of PI．This improved algorithm also overcome the shortage of difficult to tuning PI controller parameters．The simulation results indicate that this algorithm can solve the problem of terminal voltage offset effectively and control the low frequency oscillation of power grid effectively，have better robustness，and to tune parameters，providing a new effective method of the control of the stability of power system．

PSO;PI controller;Prediction function;Excitation Control

TP273

B

1674－8069(2015)03－057－04

国家高技术研究发展计划(863计划)(2013AA065401)

2014-12-26;

2015-02-27

张鹏宙(1976-)，男，副总工程师，主要从事环保装备、电除尘、计算机控制等方面研究。E－mail:51961958@qq．com