语义Tableau定理证明器的Prolog实现
高华 江建国 苏贺靓
【摘 要】语义Tableau是一种具有较强通用性和适用性的推理方法。基于Prolog语言,并利用语义Tableau方法,在M.C.Fitting提出的一阶逻辑自动定理证明器的基础上提出了一些改进,给出了改进后相应的算法,并且对算法的可终止性和正确性进行了证明。实验结果表明,优化后的语义Tableau定理证明器,大大提高推理效率。
【关键词】语义Tableau;定理证明器;Prolog
【Abstract】Semantic Tableau is a strong versatility and applicability of the method of reasoning. Basing on the Prolog language, and the use of Semantic Tableau method, it made some improvements which based on the first-order logic automated theorem proposed by M.C.Fitting, and gave the corresponding algorithm. In addition, it gives the proofs of its terminability and correctness. Experimental results shows that the optimized Semantic Tableau theorem prover makes the Tableau close early and improves greatly in time efficiency of deduction.
【Key words】Semantic tableau; Theorem prover; Prolog
0 引言
自动定理证明(Automated Theorem Proving, 简称ATP)一直是人工智能领域内的一个重大研究课题。在软件生成,软硬件验证,推理数据库等领域,自动定理证明都有着广泛的应用。研究自动定理证明的方法有很多,常见的自动定理证明的方法有两类:归结法和语义Tableau方法。有关这两种方法的应用有很多,例如许伟涛和张家锋等人都将归结法应用在格值逻辑上,并取得了重大的突破[1-2];刘全,孙吉贵根据语义Tableau方法提出了一种新的定理证明器TableauTAP[3]。
语义Tableau是在20世纪50年代由Beth和Hintikka发明的,之后由Sumullan和Fitting进一步完善。自语义Tableau问世以来,对语义Tableau自动定理证明器的探索一直吸引着广大人工智能研究者。很多文献在该方面进行了探索。
B.Becke和J.Posegga提出了一种高效、简洁、安全的一阶逻辑定理证明器leanTAP[4-5]。leanTAP系统是由五条Prolog语句构成的。由于该系统本质上利用了Prolog的搜索机制,因此用不同的语言书写该程序时,我们至少要模仿Prolog的一部分。由于程序的短小,B.Becke和J.Posegga能够对该系统的完备性和可靠性的证明做一个简述。但是其完备性证明的具体过程却相对复杂。
为了简化系统完备性的证明以及使leanTAP更容易被理解,M.C.Fitting从leanTAP中提取出了一种新的序列演算[6]。该序列演算即使在没有所有结构规则的情况下,仍具有可靠性和完备性。而且还很容易被扩展到其他的逻辑中去。
M.C.Fitting提出了另一种Tableau的一阶逻辑自动定理证明器系统[7]。该系统是在Windows环境下,应用Prolog语言实现的。其相应的可靠性和完备性的证明是采用模型存在定理来完成的。该系统的方法易于扩展,且具有很强的通用性,这使得它能够很快的被大多数人接受。只是在实现效率问题上还存在着一些不足。应用M.C.Fitting的Tableau系统相应的扩展规则,我们可以构造出一个含有n个分枝的Tableau分枝树,且该分枝树上的n-1个分枝是封闭的。然而在使用谓词closed对其进行验证时,系统又一次对整个Tableau分枝树进行了检测,这是没有必要的。
在M.C.Fitting工作的基础上,针对以上问题,本文对其算法做了相应的改进,并对改进后的算法进行了可终止性和正确性的证明。将改进后的系统与改进前的系统进行对比,结果表明,改进后的系统在推理的时间效率和空间效率上都有很大的提高。
2 Tableau算法
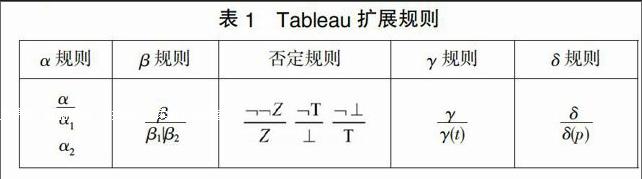
本文给出的Tableau算法是在M.C.Fitting的基础上作了进一步的改进而得出的。一方面,为防止对某分枝中已经互补的子式[8]继续扩展。系统在每次扩展之后,应立即对其封闭性做出检验,而不是等把整个Tableau分枝树都扩展完,再验证它是否为封闭的。另一方面,已经封闭的分枝,应把它去掉。否则,系统会又一次地对其进行扩展。这增加了算法的复杂度,从而导致了系统实现效率降低。
定理1 设X为公式,若X不是有效的,则算法终止,且最后终止于No;否则,算法终止于Yes。
证明:首先,该算法是可以终止的。设T为[〈X〉]中非原子公式或者是未实例化的量词公式的集合,每次循环之后,T的个数就会减少1,由于X是有限的,所以循环必将终止,即该算法终止;其次,该算法也是正确的。假设X不是有效的,但最后终止于Yes,则由循环的条件可知,该分枝树中没有其他任何分枝,即该分枝树中的所有分枝都被删去了,进而该分枝树的所有分枝都是闭的。由定义2可知,此时的Tableau是闭的,所以X有一个Tableau证明。由文献[7]中自由语义变量Tableau的可靠性可知,X是有效的。这与假设矛盾,因此系统终止于No。若X是有效的,但不以Yes终止,由算法可知,在对所有的公式都进行扩展之后,Tableau树仍是不封闭的,因此X不是有效的,这与假设矛盾。因此算法终止于Yes。
3 Prolog实现
把一个Tableau分枝树看作是由它上分枝构成的一个列表T=[B1,B2,…,Bn],列表中的每个元素Bi代表一个分枝,且每个分枝Bi也都可以写成由该分枝上所有公式构成的一个列表B=[φ1,φ2,…,φn]列表中的每个元素φi表示一个公式。若Tableau分枝树的其中的一个分枝Bi是闭的,则把此分枝从列表T中删去。最后,如果构成的Tableau分枝树的列表T为空,则有该Tableau是闭的。
由于本文构造的Tableau是严格的,因此,用Tableau扩展规则作用后的公式应从列表中删去,从而使得由每个分枝构成的列表中的元素为原子或未扩展的公式。
相对于文献[7],本文在验证分枝闭的过程中增加了对分枝闭的检验,来防止对已封闭了的分枝继续使用Tableau扩展规则进行扩展。
为证明公式X的有效性,本文将证明器的开始目标设置为:test(X,Qdepth)。X是待扩展的原公式;Qdepth是γ规则使用的次数。当Qdepth达到最大值时,程序将不再被执行。因为扩展规则中的γ规则要求从γ到γ(t),所以限制γ规则的使用次数是很有必要的。这里t是任意的闭项。由于闭项t的个数是无穷的,因此γ规则会无休止地执行下去。
程序中对公式的扩展是用谓词expand(Tree,Qdepth,Newtree)来实现的。这里,Tree是待扩展的语义分枝树;Qdepth用来限制γ规则的使用次数;Newtree是扩展之后得到的新的Tableau分枝树。对Tableau分枝的扩展是采取递归的方式进行的。扩展的实际操作过程如下:
Singlestep(OldTableau,OldQdepth,NewTableau,NewQdepth)
这里OldTableau,NewTableau分别是待扩展的分枝树和扩展完之后的分枝树;OldQdepth与NewQdepth分别是扩展前后Qdepth的值。
4 对比实验
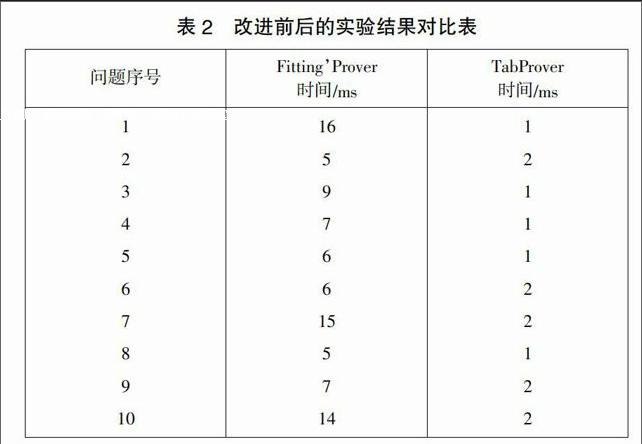
改进后的系统是在Windows环境下,应用SWI-Prolog语言实现的。使用改进后的系统对文献[9]中的10个问题进行证明,并与改进前的系统作比较,结果见表2。
由表1可以得出,改进后的系统TabProver与原系统相比较在运行时间效率方面有了很大的提高,从而本文对原系统的改进是可行有效的。
5 结语
对于自动推理而言,考察其推理效率的一个重要指标是推理所用的时间和空间。近年来随着人工智能技术的进一步发展,自动推理在效率方面的要求也越来越高,基于语义Tableau的推理系统也存在效率方面的问题。本文在M.C.Fitting的基础上针对分枝闭检验的效率问题提出了相应的改进。改进后的系统,一方面增加了封闭性的检验;另一方面对已经封闭的分枝采取立即删除。此外,本文还给出了改进后的算法,证明了算法的正确性与可终止性,并在Windows环境下对系统进行了实现。实验结果表明,改进后系统的推理复杂度大大降低了。
原有的一阶逻辑自动定理器由于涉及对量词的处理,因此导致了该证明器的运行效率相对较低,这给人们带来了不便。今后将要进行的工作是:通过引入斯科拉姆化方法消去公式中的存在量词,并验证是否可以提高相应的效率。此外,由于语义Tableau方法具有较强的通用性,因此可以尝试将其扩展到非经典逻辑中,从而达到该方法在不同领域的应用。
【参考文献】
[1]XU Wei-tao ZHANG Wen-qiang ZHANG De-xian et al. α-generalized resolution principle based on the lattice-valued first-order logic system[J]. Journal of XiDian University,2014, 41(1):135-139.许伟涛,张闻强,张德贤,等.格值一阶逻辑系统的α广义归结原理[J].西安电子科技大学学报,2014,41(1):135-139.
[2]ZAHNG Jia-feng, XU Yang. α-semantic resolution method based on lattice-valued first-order logic LF(X)[J]. Computer Science, 2014, 41(9):274-279.张家锋, 徐扬. 格值一阶逻辑LF(X)中的α-语义归结方法[J]. 计算机科学,2014,41(9):274-278.
[3]LIU Guan, SUN Ji-gui. Theorem proving system based on tableau-tableauTAP[J]. Computer Engineering, 2006, 32(7):38-46.刘全,孙吉贵. 基于Tableau的定理机器证明系统TableauTAP[J].计算机工程, 2006,32(7):38-46.
[4]B BECKERT, J POSEGGA, LEANTAP. Lean tableau-based deduction[J]. Journal of Automated Reasoning, 1995,15(3):339-358.
[5]B BECKERT, J POSEGGA. Logic programming as a basis for automated deduction[J]. The Journal of Logic Programming, 1996,28(3):231-236.
[6]M FITTING. LeanTAP revisited[J]. Journal of Logic and Computation, 1998, 8(1):33-47.
[7]M C FITTING. First-order logic and automated theorem proving[M]. 2rd ed. Springer-Verlag, 1996.
[8]LIU Guan, SUN Ji-gui, YU Wan-jun. An improved method of δ-rule in free variable semantic tableau[J]. Journal of Computer Research And Development, 2004,41(7):1068-1073. 刘全,孙吉贵,于万钧.自由变量语义Tableau中δ规则的一种改进方法[J].计算机研究与发展,2004,41(7):1068-1073.
[9]F J PELLETIER. Seventy-five Problems for testing automatic theorem provers[J]. Journal of Automated Reasoning, 1986,2:191-216.
[责任编辑:汤静]

