木材动态力学特性对热磨过程能耗的影响1)

许威 花军 陈光伟 张绍群

(东北林业大学，哈尔滨，150040)

纤维分离过程的电能消耗在纤维板生产中所占的比重很大，通常热磨机的电耗占生产总电耗的40%～50%［1-2］，直接影响企业的生产成本与利润。探索影响纤维分离过程能耗的因素，降低纤维分离过程中的能耗，一直是纤维板和造纸设备生产企业以及相关学者研究的重点内容。很多国外学者利用试验，从冲击速度、受载方向、试验温度、蒸汽预处理等方面，研究了热磨条件下木材原料的力学性能及其对纤维分离过程能耗的影响［3-8］。目前，国内相关研究较少;但是，国内学者对静态及准静态加载条件下木材的断裂力学已开展了大量的研究［9-14］，并将分形理论引入到木材断裂的研究中［15-17］，对热磨条件下木材原料力学性能的研究具有重要的借鉴与参考价值。

虽然国外对热磨机研磨条件下木材原料力学性能的研究开展较早，但是，绝大部分的研究都是在准静态或应变率较低的环境下进行的，这导致研究得到的结果严重脱离了生产的实际情况。本研究的目的，在于利用分离式霍普金森杆(SHPB)对木材试件进行高应变率的压缩试验，分析木材动态力学特性对热磨过程能量消耗的影响。试验包含3 个应变率(400、700、1 000 s-1)、2 个含水率(气干、全饱和)、3 个加载方向(弦向、径向、轴向)。3 个应变率，是为了分析高应变率加载下，应变率对木材动态力学特性的影响，进而分析热磨机转速对热磨过程中能量消耗的影响。2 个含水率，全饱和是为了接近热磨过程中原料的真实含水率，气干则是为了和全饱和作对比。3 个加载方向，是为了研究高应变率加载条件下，不同加载方向上木材动态力学特性与其破碎解离状态的差异，进而确定热磨过程能耗最少的最佳进料方向，合理设计磨片机构。

1 材料与方法

1．1 试件制作

试验选取纤维板生产中常用的杨木(Populus davidiana Dode)作为试验材料，产自黑龙江省，直径为32 cm。参照GB/T 1929—2009 和GB/T 1935—2009 截取试样毛坯并制作试件，试件毛坯均在同根试材的边材处截取，试件尺寸为25 mm×25 mm×20 mm。气干试件，是将试件放到温度为25 ℃的室内，待试件含水率达到平衡，试件含水率约为12．81%。全饱和试件，是将试件浸泡在水中2 d 以上，待试件含水率达到全饱和状态。试件20 mm 方向为加载方向(见图1)。共有18 组实验，每组试验包含4 次重复试验，所有试验在室温(约25 ℃)条件下进行。

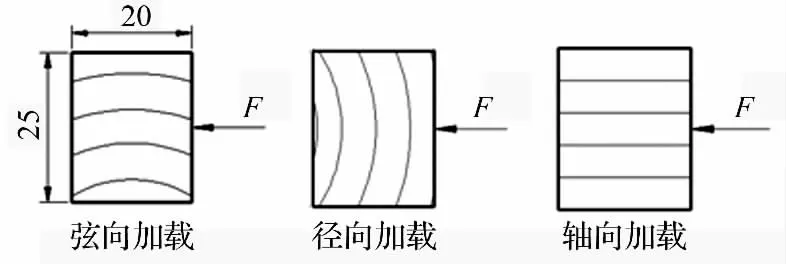
图1 试件尺寸及加载示意图(单位:mm)

1．2 试验方法

高应变率压缩试验是在SHPB 上完成，SHPB技术是获得材料在102～104s-1应变率范围内动力学特性的主要试验手段［18］。利用SHPB 技术测试材料动态力学特性时，若测试材料的波阻抗与SHPB杆材料之间的波阻抗相差过大会导致透射杆中透射脉冲信号非常弱，影响试验的测试精度［19］。由于木材是一种低密度、低波阻抗的材料，为了解决波阻抗的匹配问题，试验选用密度和弹性模量相对较低的铝杆。同时，考虑到木材波阻抗较低造成透射脉冲信号强度较弱，应用普通应变片进行测试，获得的信号信噪比较低;试验中透射杆上采用半导体应变片测试透射脉冲信号，对于脉冲信号强度较高的入射脉冲仍用普通应变片进行测试。

本试验所用SHPB 试验装置:入射杆、透射杆、子弹长度分别为1 800、1 800、300 mm，直径均为40 mm 的铝杆，其弹性模量为71 GPa，密度为2 700 kg/m3。在入射杆、透射杆距离试件1 000 mm 处，分别粘贴普通应变片和半导体应变片，用于测定脉冲信号。用Matlab 和Excel 软件，对采集到的脉冲信号进行计算分析。

1．3 数据处理

试验时，SHPB 杆中应力脉冲的传播如图2 所示。子弹沿着轴向给入射杆一个冲击加载(F0)，在入射杆中产生一个单轴应力脉冲σ(t)并对试样进行加载。

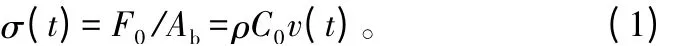
式中:Ab为入射杆与透射杆的横截面积;C0为杆中应力脉冲的传播速度，C0=dx/dt;v(t)为质点速度;ρ为子弹的密度。

入射杆中的质点以速度vi向右传播，入射脉冲的幅值由冲击速度(是气压的函数)和子弹的材料属性决定。在动态冲击研究中，准确测量应力脉冲和质点速度是非常重要的，忽略应力脉冲传播过程中的横向效应，认为入射杆、透射杆与试件接触的交界面处合力为0。根据试件与杆接触表面速度的连续与力的平衡情况，得出试样质点的速度(vs):

式中:σi为入射应力脉冲;σr为反射应力脉冲;E0为杆材料的杨氏模量。

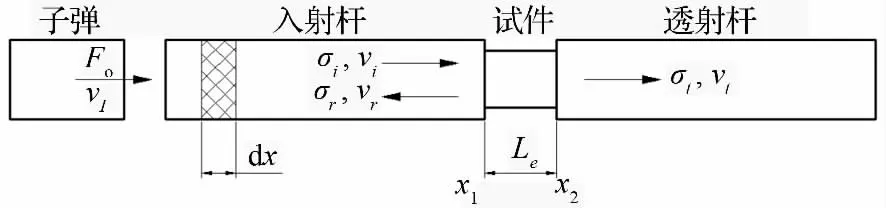
图2 SHPB 中应力脉冲传播示意图

试件相对变形(δn(t))，在应力脉冲的传播方向上试件的有效长度(Le)，t 时刻由应力脉冲在x1和x2的位移U1(t)、U2(t)得出:

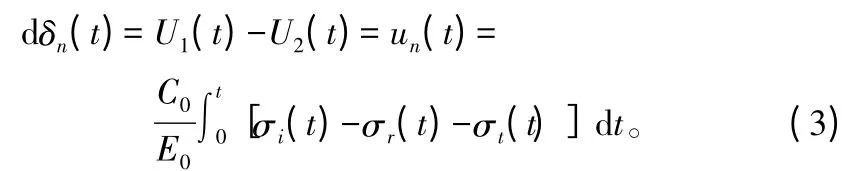
式中:σt为透射应力脉冲。

试件应变εs(t)用(4)式计算:

用SHPB 试验时，试件被夹在入射杆与透射杆之间。将胡克定律σ=Eε 代入(3)式，并结合(4)式，得试件的应变:

由试件的平衡有εt(t)≈εi(t)+εr(t)，所以试件应变为:

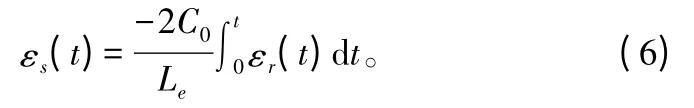
试样的平均应力为:

式中:As为试件受载方向的横截面积。

2 结果与分析

对各组试验所得数据取平均值列于表1;在下面的论述中，各组试验应变率的数值均取整，分别为400、700、1 000 s-1(见表1)。

2．1 试件受载后解离特征

当应变率为400 s-1时，只有全饱和试件弦向加载后碎成了几大块，其余组试件均只发生塑性变形。

当应变率为700 s-1时，气干试件:弦向、径向加载，均有沿加载方向的裂纹产生;轴向加载，在加载方向上纤维发生褶皱并沿长度方向产生劈裂。全饱和试件:弦向加载，解离成很多小块，并且有一些火柴棍状的小试件;径向加载，沿加载方向产生裂纹，并且解离成几大块;轴向加载，在加载方向上纤维发 生较轻微的褶皱。

表1 试验测得试件动态力学特性

当应变率为1 000 s-1时，气干试件:弦向、径向加载，产生更多的裂纹，并且有大块试件剥离;轴向加载，被解离成很多小段试件，并且每段试件上都有非常明显的褶皱。全饱和试件:弦向加载，解离成很多小块，并且有大量的火柴棍状的小试件;径向加载，解离成更多的大块试件;轴向加载，在加载方向上纤维发生非常明显的褶皱现象，并且在加载面上纤维发生了明显的压溃现象(见图3)。

图3 应变率为1 000 s-1时试件破坏状态

从整体看，全饱和试件较气干试件更容易解离，而弦向最易解离，径向次之，轴向最难解离;弦向、径向解离时不会折断纤维，轴向解离时纤维会发生褶皱现象并最终折断纤维。轴向发生褶皱时，破坏线与轴线的夹角主要受自身物理性质的影响，是一种材料属性［20］，气干试件破坏线与主轴的倾角约为70°，全饱和试件破坏线与主轴的倾角约为55°。

2．2 试件质点速度—位移关系

对比分析各组试验试件质点速度—位移曲线发现:试件质点速度—位移曲线的形状，不受应变率、加载方向和含水率的影响;试件质点的速度近似呈弧线形急剧增加的，在达到最大速度后呈波浪状直线减小，然后又呈弧线形急剧下降，直至速度为0;试件质点速度的大小，不受或很少受含水率和加载方向的影响，但随应变率的增加而增加(见图4)。Allazadeh［21］指出，干枫树受压缩加载时，试件质点速度—位移曲线是分三段急剧增加的，且质点速度不受试件厚度的影响。结合Allazadeh 的研究结果可以推断出，试件质点速度—位移曲线是受材料自身的物理性质(如强度、密度等)和加载条件的影响，相当于材料的一种属性。

2．3 试件的强度

由表2 可见:气干试件的抗压强度随应变率的加大而增加，具有非常明显的应变率效应;在同一个应变率范围内，弦向抗压强度最小，轴向抗压强度最大，具有高度的各向异性。

由表2 可见:全饱和试件，各组试验的抗压强度并没有像气干试件那样明显、一样的规律。从整体看，在同一个应变率范围内，还是弦向抗压强度最小，轴向抗压强度最大。当应变率从400 s-1增加到700 s-1时，弦向、径向、轴向的抗压强度，分别增加了34．12%、42．82%、13．90%;当应变率从700 s-1增加到1 000 s-1时，轴向的抗压强度增加了2．73%，弦向、径向的抗压强度分别减少了2．42%、24．24%。可见，当应变率在400 ～1 000 s-1内变化时，轴向抗压强度的值随应变率的增加而增大，但增加幅度随应变率的增加而减小;弦向、径向抗压强度随应变率的增加先增大而后减小，全饱和试件抗压强度也具有非常明显的应变率效应。

图4 试件质点位移—速度曲线

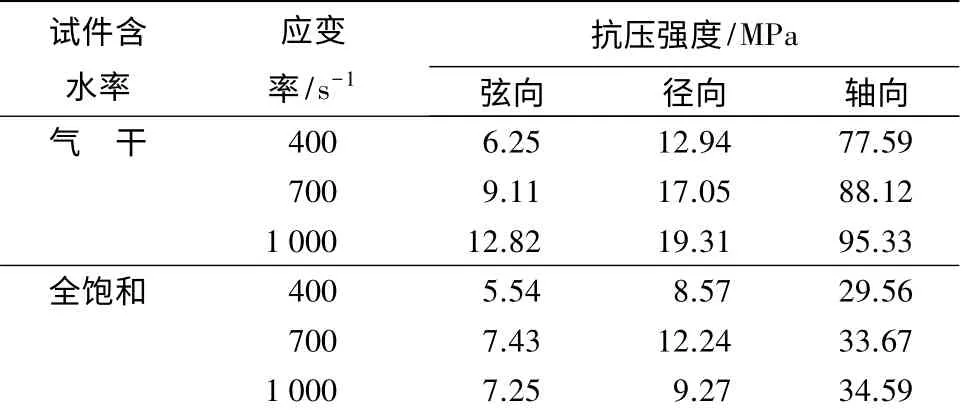
表2 试件抗压强度

对比气干、全饱和试件的试验结果发现:同一应变率范围内，气干试件的抗压强度大于全饱和试件抗压强度。

虽然气干和全饱和试件均具有明显的应变率效应，但气干与全饱和试件随应变率的变化规律并不相同。气干试件的抗压强度随应变率的增加而增加，全饱和试件弦向、径向的抗压强度随应变率的增加先增大而后减小。可以推断，这一现象是由木材中的自由水和应变率共同作用产生的。杨木属于阔叶材，而阔叶材中水分的移动路径主要是导管，另外，还包括管胞、导管状管胞等。导管上具有穿孔和纹孔，在轴向上水分通过穿孔从一个导管进入纵向邻近的另一个导管，在弦向、径向上水分通过导管壁上的纹孔移动［22］。木材受载时，由于移动路径孔径大小的不同、不同方向移动路径不同，木材中自由水的移动会受到很大阻碍;并且阔叶材导管中的侵填体、闭塞纹孔以及纹孔膜上的抽提物的存在，也会阻碍自由水的移动。若木材受载时提供给自由水的能量足够破坏木材的结构，这种情况下，自由水对木材的结构起到一种减弱作用。试件质点速度的大小，不受或很少受含水率和加载方向的影响，但随应变率的增加而增加，可知，自由水获得的能量大小主要受应变率的影响并随应变率的增加而增加。

实际生产中，可以通过提高热磨机的转速提高研磨过程中木材原料的应变率，所以提高热磨机的转速可以降低木材原料的抗压强度，从而减少研磨过程中的能量消耗。Stationwala 等［23-25］研究发现，提高热磨机转速可以降低能量消耗，这与本研究的结果一致。

3 结论

全饱和试件比气干试件更易解离。

在同一个应变率范围内，弦向抗压强度最小，轴向抗压强度最大。进料时，若能使大部分原料沿着弦向进料，而避免沿着长度方向进料，则会减少研磨过程中的能量消耗。

当应变率在400～1 000 s-1范围内变化时，轴向的抗压强度值随应变率的增加而增大，但增加幅度随应变率的增加而减小;弦向、径向的抗压强度，随应变率的增加先增大而后减小。热磨过程中，增大磨盘转速提高纤维分离过程的应变率，可减少热磨过程中的能量消耗。

致谢:哈尔滨工业大学空间碎片高速撞击研究中心张伟教授、任鹏博士，对试验顺利完成和数据处理工作给予帮助，谨此致谢!

［1］ 陈光伟，花军，纪伟，等．磨片结构对纤维分离过程中能量转换机理的影响［J］．东北林业大学学报，2010，38(8):109-110，114．

［2］ 陈光伟，花军．纤维产量和质量对热磨机能耗影响的机理分析［J］．东北林业大学学报，2009，37(6):40-41，47．

［3］ Jan-Erik Berg． Effect of impact velocity on the fracture of wood as related to the mechanical pulping process［J］． Wood Science and Technology，2001，35(4):343-351．

［4］ Atack D，May W D，Morris E L，et al． The energy of tensile and cleavage fracture of black spruce［J］． Tappi J，1961，44(8):555-567．

［5］ Eskelinen E，Hu S H，Marton R． Wood mechanics and mechanical pulping［J］． Australasian Pulp and Paper Industry Technical Association(Journal)，1982，36(1):32-38．

［6］ Uhmeier A，Salmén L． Influence of strain rate and temperature on the radial compression behavior of wet spruce［J］． Journal of Engineering Materials and Technology，1996，118(3):289-294．

［7］ Kärenlampi Petri P，Tynjälä Pekka，Ström Pasi． Dynamic mechanical behavior of steam-treated wood［J］． Mechanics of Materials，2002，34(6):333-347．

［8］ Holmgren S E，Svensson B A，Gradin P A，et al． An encapsulated Split Hopkinson pressure bar for testing of wood at elevated strain rate，temperate，and pressure［J］． Experimental Techniques，2008，32(5):44-50．

［9］ 孙艳玲，鹿振友．木材断裂力学的研究［J］．北京林业大学学报，1997，19(3):85-92．

［10］ 孙艳玲，赵东，高继河．数字散斑相关方法在木材断裂力学上的应用分析［J］．北京林业大学学报，2009，31(增刊1):206-209．

［11］ 田振农，张乐文．木材的宏观力学模型及断裂机理［J］．北京林业大学学报，2010，32(2):153-156．

［12］ 邵卓平，江泽慧，任海清．线弹性断裂力学原理在木材中应用的特殊性与木材顺纹理断裂［J］．林业科学，2002，38(6):110-115．

［13］ 邵卓平，任海清，江泽慧．木材横纹理断裂及强度准则［J］．林业科学，2003，39(1):119-125．

［14］ 邵卓平，童永耀，盛宏玉，等．木材裂纹尖端应力场的有限元分析和开裂方向预算［J］．林业科学，2010，46(10):108-113．

［15］ 许威，张绍群，陈光伟，等．分形理论在木材断裂研究中的应用与进展［J］．木材加工机械，2011(6):36-39．

［16］ 费本华，赵勇，覃道春，等．应用CT 技术研究木材断口形态特征［J］．林业科学，2007，43(4):137-140．

［17］ 张绍群，花军，许威，等．基于三维扫描技术的木材断口分形特征［J］．林业科学，2014，50(7):138-142．

［18］ 姜风春，沙桂英，张晓欣，等．Hopkinson 压杆实验技术的应用研究［J］．哈尔滨工程大学学报，1999，20(4):56-60．

［19］ 余同希，邱信明．冲击动力学［M］．北京:清华大学出版社，2011:39．

［20］ 刘一星，赵广杰．木质资源材料学［M］．北京:中国林业出版社，2004:196-197．

［21］ Allazadeh M R，Wosu S N． High strain rate compressive tests on wood［J］． Strain，2012，48(2):101-107．

［22］ 刘一星，赵广杰．木质资源材料学［M］．北京:中国林业出版社，2004:138-139．

［23］ Stationwala M T，Atack D，Wood J R，et al． The effect of control variables on refining zone conditions and pulp properties［J］． Paperi Ja Puu，1991，73(1):62-69．

［24］ Stationwala M I，Miles K B，Karnis A． The effect of first stage refining conditions on pulp properties and energy consumption［J］．Journal of Pulp and Paper Science，1993，19(1):12-18．

［25］ Stationwala M I，Miles K B，Karnis A． Effect of feed rate on refining［J］． Journal of Pulp and Paper Science，1994，20(8):236-240．