聚乙烯基木塑复合材料动态弹性模量预测模型1)

冯莉 赵春雁 那晓雁

(东北林业大学，哈尔滨，150040) (昆明理工大学)

近年来木塑复合材料的制造技术日趋成熟，其制备方式、常用材料也比较固定。可以通过制备方式、材料等相关因素建立一种评价模型对木塑复合材料的力学性能进行预测。目前国内关于木塑复合材料的相关标准还不完善，所以对其力学性能的研究还很有限，特别是与静态弹性模量有密切相关性的动态弹性模量［1］。动态弹性模量是衡量木塑复合材料力学性能的一项重要指标，在材料的应用以及改性和微观的结构研究中具有重要的作用［2］。动态弹性模量是衡量材料变形难易程度的表征，例如在材料的蠕变行为研究中与材料变形的仿真研究中，弹性模量都是必须要考虑到的因素。回归预测法是一种应用较广泛的分析方法，是指根据预测的相关性原则找出影响预测目标的各因素，利用数学方法建立近似表达式，再进行模型的误差检验确定预测模型，并对其进行预测。灰色理论认为系统的行为现象具有朦胧、数据复杂、有一定规律性，是有整体功能的。灰数的生成，就是从杂乱中寻找出规律。灰色预测的数据是通过生成数据的GM(1，N)模型所得到的预测值的逆处理结果［3］。笔者利用无损检测的方法检测PE 基木塑复合材料的动态弹性模量，并通过上述方法建立动态弹性模量预测模型，分析各预测模型的特点，找出一种更为适合预测动态弹性模量的预测模型。

1 材料与方法

木粉:为杨木粉，40 ～60 目。聚乙烯(PE):PE、LA、50D012(5000S)，大庆石化。偶联剂:接枝HDPE 相容剂CMG9804，南通日之升高分子新材料科技有限公司。

双螺杆混配挤出机，SJSH-30 同向啮合双螺杆挤出机，南京橡塑机械厂;单螺杆挤出机，SJ-45，南京橡塑机械厂;纤维含水率测定仪，C69-OZC 型水分快速测定仪，上海第二天平仪器厂。

将HDPE、木粉(含水率＜3%)、偶联剂按照试验配方计量后加入高速混合机将物料混合均匀待造粒使用。为了清晰地表述各项加工工艺参数方便进行后续分析，把本次试验过程中的成型温度、螺杆转速、m(木粉)∶m(聚乙烯)、偶联剂质量分数和造粒温度作为工艺参数变量，并用正交试验方法进行试验设计(见表1)。按照L16(45)方案，把试件分为16 组，每组8 个试件。通过单螺杆挤出机挤出后的试样为40 mm×4 mm，按照GB/T 9341—2000 推荐试验尺寸裁成80 mm×10 mm×4 mm，用于材料性能测试。

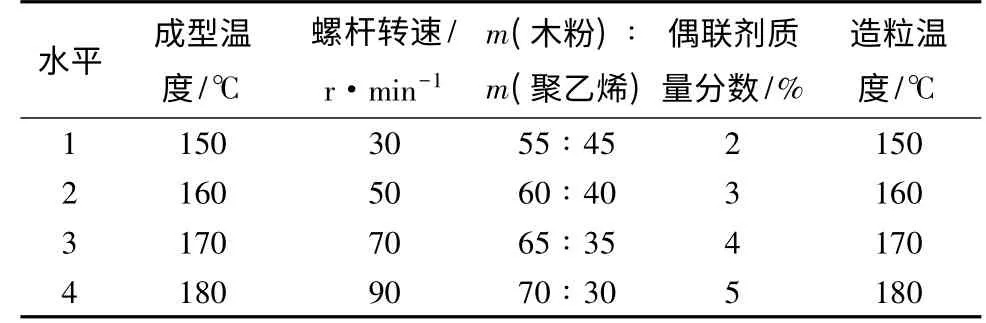
表1 因素水平表

根据弯曲振动理论进行实验，在弯曲振动的节点处(0．224 L)处用小支架将试件支起，用小锤敲击试件的一端，另一端用麦克接收信号。信号经过放大后，传到FFT 分析仪进行解析，得到共振频率。每次测定取前4 个(包括基频在内)共振频率，利用式(1)可求得弯曲振动动态弹性模量［4］。

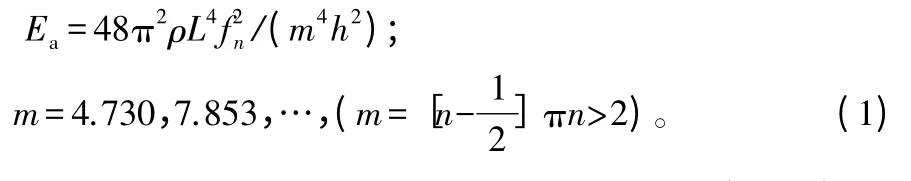
式中:Ea为弯曲振动法所测得的弹性模量(GPa);fn为试件固有频率(Hz);ρ 为试样的密度(g/cm3);h为试件厚度(cm);L 为试件长度(cm);m 为伯努利方程参数。

2 结果与分析

根据弯曲振动检测方法所得的动态弹性模量实验结果见表2。可知各个试件实验结果的标准差与变异系数都比较小，数据的分散程度比较小，实验结果比较稳定，能够保证真实的实验结果。

2．1 动态弹性模量的回归模型建立

利用SPSS 数学分析软件对试件的加工因素和所得的弯曲振动弹性模量进行了回归分析，旨在分析各个加工因素对PE 基木塑复合材料动态弹性模量的影响程度，并选择相关性比较大的加工因素进行预测模型的建立。由于木塑复合材料的配方中木粉占比很大，且木粉不是一个性能稳定的材料，在制成板材后有很多因素会对密度产生影响，如温度、湿度、木粉的纯净度、木材自身的力学性能差异(木材不同部分、生长环境不同等对性能影响)等，还有一些未知因素都会对密度产生影响。上述某些因素是不可控的，所以将密度作为一个表征参数。将加工工艺和密度作为因变量，并将其与动态弹性模量利用SPSS 软件进行回归分析(向后法)。在显著性检验中造粒温度、m(木粉)∶m(聚乙烯)、螺杆转速的显著性检验值均大于0．05，为无统计学意义的因素，所以将其剔除。模型的相关系数R=0．976，调整R2=0．919，说明因变量有91．9%可由自变量解释;标准误差很小，说明拟合程度良好;方差分析显著性检验值远远小于0．05，说明回归效果显著。

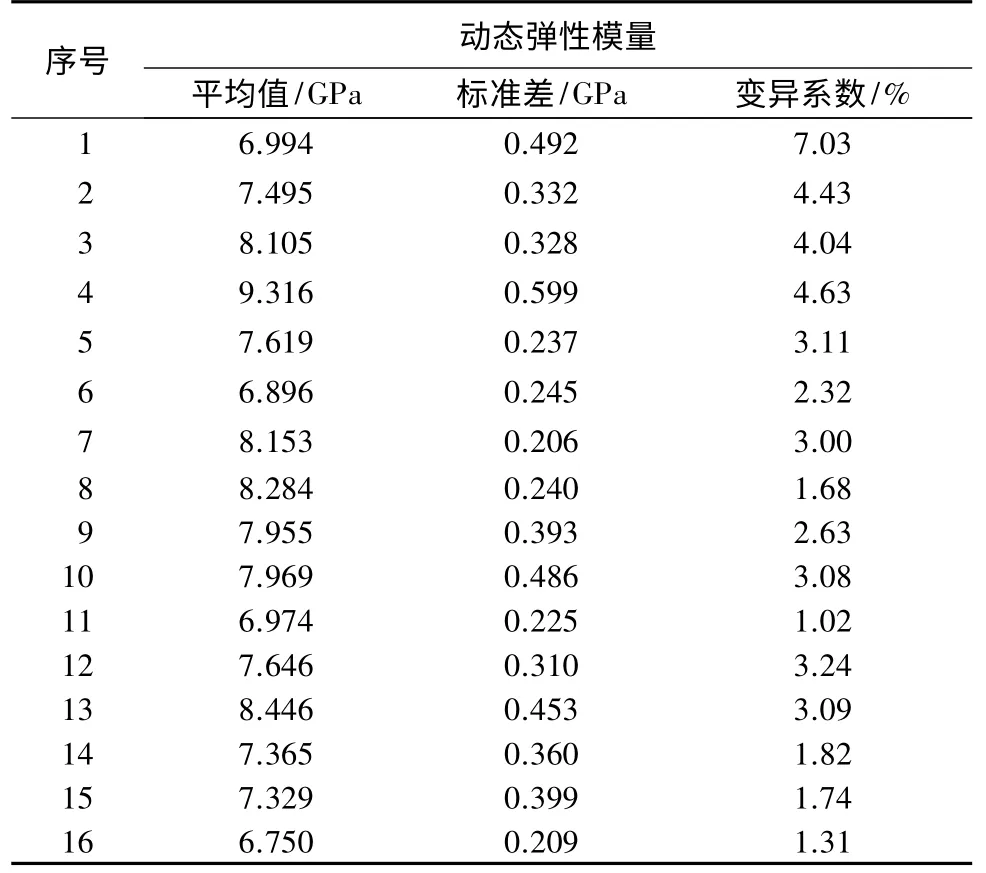
表2 弯曲振动动态弹性模量

由表3 可知方程回归的显著性检验值都非常小，且多重共线性诊断结果表明不存在多重共线性。因此可以通过成型温度、偶联剂质量分数、密度3 个因素对PE 基木塑复合材料的动态弹性模量进行预测，回归方程如下:

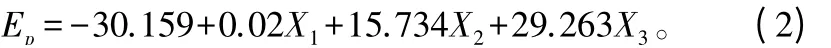
式中:X1为成型温度;X2为偶联剂质量分数;X3为密度。

2．2 基于灰色理论系统的GM(1，N)建模

为了解各个因素对动态弹性模量的关联程度，将加工因素和密度与动态弹性模量进行关联度的计算，结果为成型温度、螺杆转速、m(木粉)∶m(聚乙烯)、偶联剂质量分数、造粒温度与密度的关联度分别为0．915 5、0．585 4、0．794 5、0．653 7、0．916 8、0．928 9。其中成型温度、造粒温度、密度的关联度均大于0．9，可知其对动态弹性模量的影响较大。但是螺杆转速、m(木粉)∶m(聚乙烯)、偶联剂质量分数对动态弹性模量的影响也不容忽视，因此在建模过程中亦应该给予考虑，所建立预测模型如下:

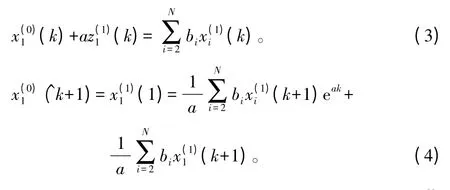
式(3)为GM(1，N)模型，式(4)为GM(1，N)的近似时间响应式，多采用式(4)进行系统行为特征值的预测。

表3 回归系数

2．3 GM(1，N，X(0))派生模型建模)称为GM(1，N)模型的定义式，其派生模型GM(1，N，X(0))如下:

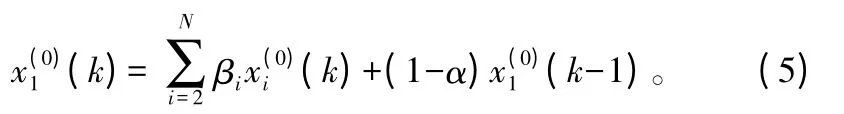
GM(1，N，X(0))是通过原始模型推导出的一种派生形式，其具有重要的性质，即数据的单层性。数据的单层性使得在处理问题过程中GM(1，N，X(0))能够有效减少累计误差提高预测精度［5］。

2．4 回归模型、GM(1，N)模型、GM(1，N，X(0))模型预测结果

回归模型与GM(1，N)模型预测结果见表4。数值经过计算得出回归模型预测结果的平均相对误差为4．478%，GM(1，N)预测模型的平均相对误差为3．981%，GM(1，N，X(0))预测模型的平均相对误差为2．599%。GM(1，N)模型相比回归模型的预测误差提高了11．098%，而GM(1，N，X(0))模型则比GM(1，N)模型的预测精度提高了34．714%。GM(1，N，X(0))模型相对于回归模型提高到41．96%。由此可以得出预测模型的精度从高到低依次为GM(1，N，X(0))模型、GM(1，N)模型、回归模型。

表4 表明回归模型第一个预测值误差是最大的，而GM(1，N)模型的第一个预测值属于异常数据，实际上第二个数据才是其第一个预测值，并且它也明显大于该模型的其他预测值。由此可见回归模型与GM(1，N)模型在对数值拟合预测初期都处于不稳定阶段，并且可以看出回归模型的趋于稳定的速度要优于GM(1，N)模型。可看出GM(1，N，X(0))模型相对上述两个模型有了很大提高，GM(1，N，X(0))模型的第一个预测值的相对误差不足1%，而后面的预测值相对误差范围也比较稳定，基本在2%～6%的范围内，具有比较好的精度，可以满足实际工程中的预测精度。

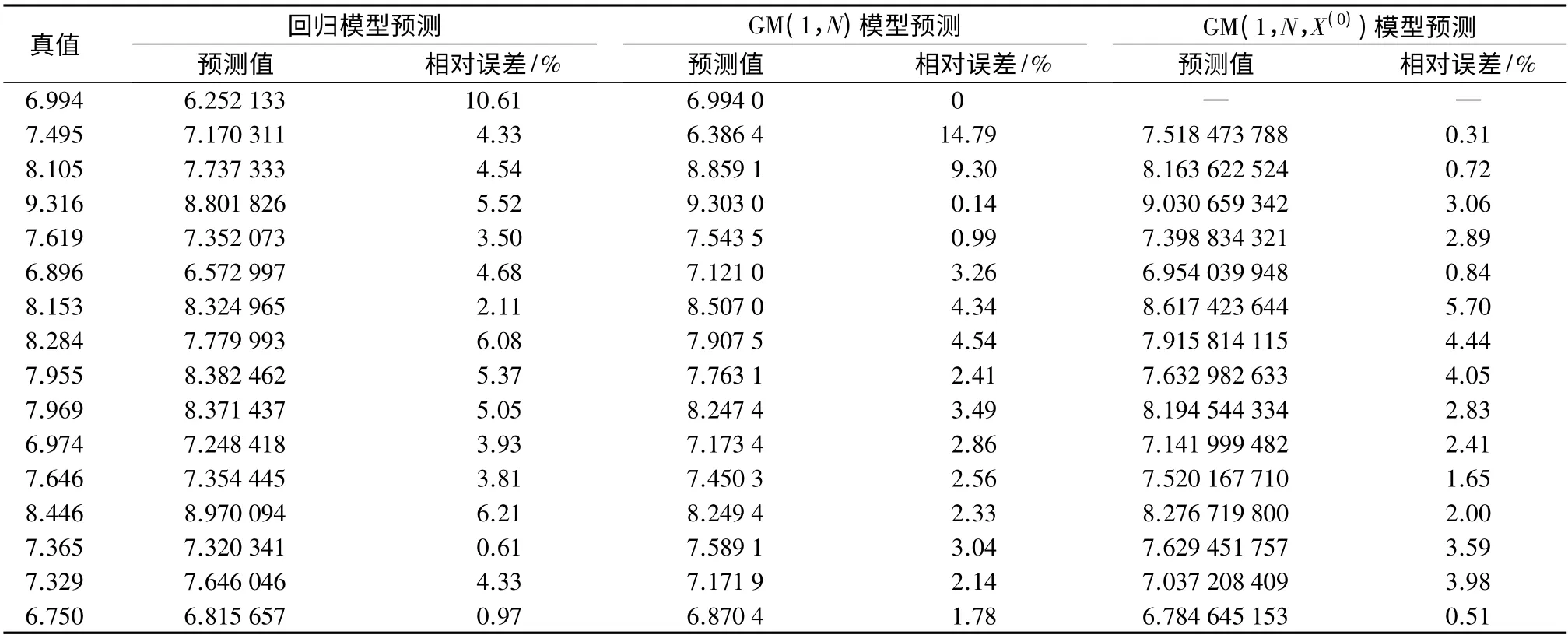
表4 模型预测结果

3 结论

根据灰色关联度结果所示各因素对动态弹性模量的影响程度从大到小依次为密度、造粒温度、成型温度、m(木粉)∶m(聚乙烯)、偶联剂质量分数、螺杆转速。利用GM(1，N，X(0))预测模型可以对PE基WPC 动态弹性模量的发展方向进行较好的预测。对于PE 基木塑复合材料动态弹性模量的预测模型其精度从高到低依次为GM(1，N，X(0))模型、GM(1，N)模型、回归模型。

［1］ 周海宾，任海青，费本华，等．木制复合板弯曲、剪切弹性模量动态测试［J］．建筑材料学报，2007，10(5):561-565．

［2］ 阮锡根，余观夏．木材物理学［M］．北京:中国林业出版社，2005．

［3］ 邓聚龙．灰色理论基础［M］．武汉:华中科技大学出版社，2002:56-79．

［4］ 胡英成．木质复合材料的动态特性与无损检测［M］．哈尔滨:东北林业大学出版社，2004:65-67．

［5］ 申志涛．基于灰色系统理论的商品住宅价格分析［D］．大连:大连理工大学土木水利学院，2010．