基于自适应阈值处理的WSN协作时间同步算法①

赵 弦

（桂林电子科技大学 信息与通信学院，广西 桂林 541004）

随着无线传感器网络应用范围的不断扩大，对时间同步的精度要求也越来越高。根据发送的同步报文不同，无线传感器网络时间同步机制可分为基于分组消息交换的时间同步协议和基于脉冲传输的时间同步协议。典型的基于分组消息交换的时间同步协议，如TPSN（timing－sync protocol for sensor networks）算法［1］、FTSP（flooding time synchronization protocol）算法［2］和EETS（energy－efficient time synchronization）算法［3］很难做到同时兼顾同步精度和能耗，且有些算法的同步误差随跳距累积，难以扩展到高密度无线传感器网络。基于脉冲传输协议的协作同步技术［4－5］，采用空间平均解决了误差累积问题，网络中节点采取相同的算法，具有较好的可扩展性和同步开销均衡性。

2006年Hu［5］提出的协作时间同步技术，其主要思想是节点缓冲来自于多个邻居节点的同一时刻的时间数据，通过对这些数据进行均值处理来提高时间同步精度；预测参考节点发射下一个脉冲的时刻，并在该时刻也发送脉冲，实现全网节点之间的同步性。然而，随着跳数增加，协作同步技术面临一些问题，临近同步状态时同步交互消息数量急剧增加产生信道争用，进而导致发送时延增加，时间同步精度降低，且节点不停地在监听和发送之间转换，能耗增加。

为了减少信道争用和降低能耗，基于协作同步技术的空间平均算法，提出一种无线传感器网络自适应阈值处理的协作时间同步算法（ATCTS）。该算法在发送脉冲时，随机退避一定的时间，接收方采用萤火虫同步技术的自适应机制［6－8］和阈值处理，并通过减少节点发送脉冲的次数，减少信道争用和降低网络能耗；利用网络节点密度高，引入协作中继，缩短了同步消息的传播距离，降低了节点的发射功率，进而节省了节点的能耗。

1 自适应阈值处理协作时间同步算法

在WSN节点密度较高的情况下，采用协作时间同步算法（CTS）时，协作节点可视为原通信节点之间的中继节点，如图1所示［9］。图1中，左边区域为节点1的发射区域，右边为节点2的接收区域，中间为中继节点M的覆盖区域。根据自由空间路径损耗模型，容易证明，传送距离相同的情况下，协作中继消息传送的能耗低于单跳消息传送的能耗。

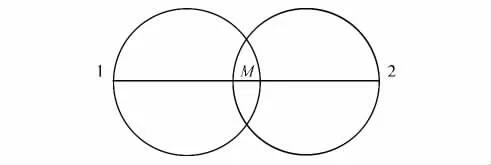
图1 协作同步模型Fig.1 The model of cooperative synchronization

无线传感器网络中，每个节点都有一个隶属于自己的本地时间。假设节点1的时钟为参考时间c1，c1（t）＝t，任意一个节点i的时间可表示为

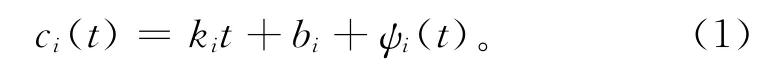
其中：ki为频率偏移，满足1－ρ≤ki≤1＋ρ，ρ为绝对频差上界，取值由晶振生产商决定，一般在10－6～10－4；bi为节点i与节点1的时间偏差，即时钟偏移；ψi（t）为随机时钟抖动，满足ψi（t）～Ν（0，σ2）。

1.1 算法描述

假设在q跳网络中，Thi为第h跳的节点i接收到m个同步脉冲的时间，Dhi为节点i发送同步脉冲前随机退避的时间延迟，g为发送脉冲间隔时间，Ts为同步脉冲序列的发送周期，t0为同步周期开始计时时间。发送脉冲时，加入随机延迟，目的是为了避免临近同步状态时，因发送脉冲的节点个数增加而产生信道争用。接收方接收到脉冲信号后将其按照发送的先后顺序放入缓冲区，等待当前周期脉冲序列发送结束，再进行处理。

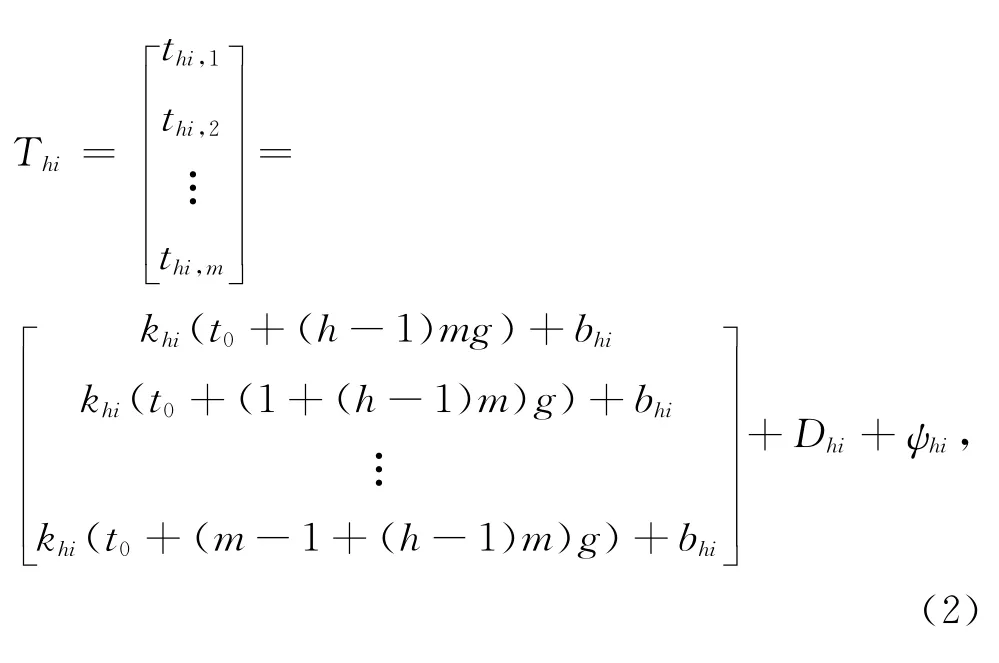
对Thi进行处理：

其中，（Ts（h－1）＋［0g…（m－1）g］Τ）为参考节点发射同步脉冲序列的时间。将tc与阈值时间T比较，第h跳的任意节点i满足的时间有组，再对节点i的组时间数据进行平均，则第h跳节点接收到脉冲的时刻可表示为：

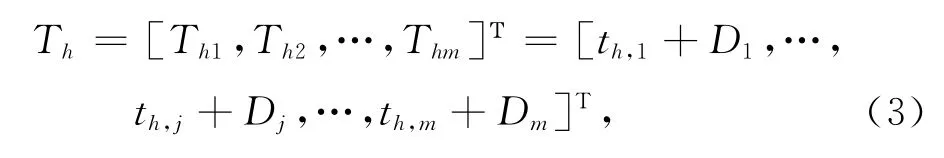
其中：h＝1，2，…，q，2，…，m；式（3）可建立线性模型［10］：

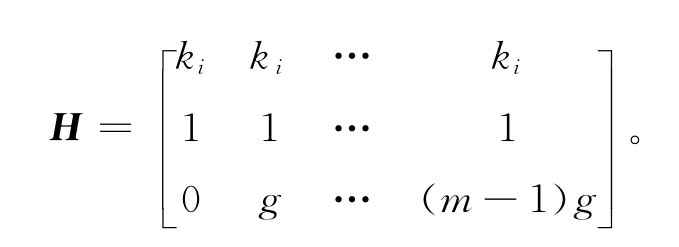
根据最佳线性无偏估计，BLUE估计量为：

预测参考节点发射下一组同步脉冲的时间为：

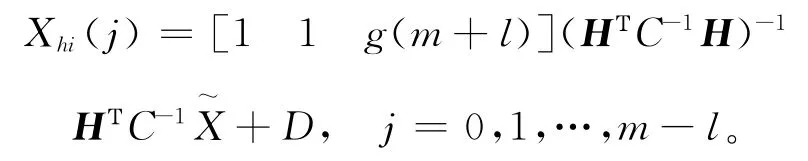
由于ki满足1－ρ≤ki≤1＋ρ，为了计算方便，设ki＝1，计算频率偏移和时钟偏移的期望和方差分别为：

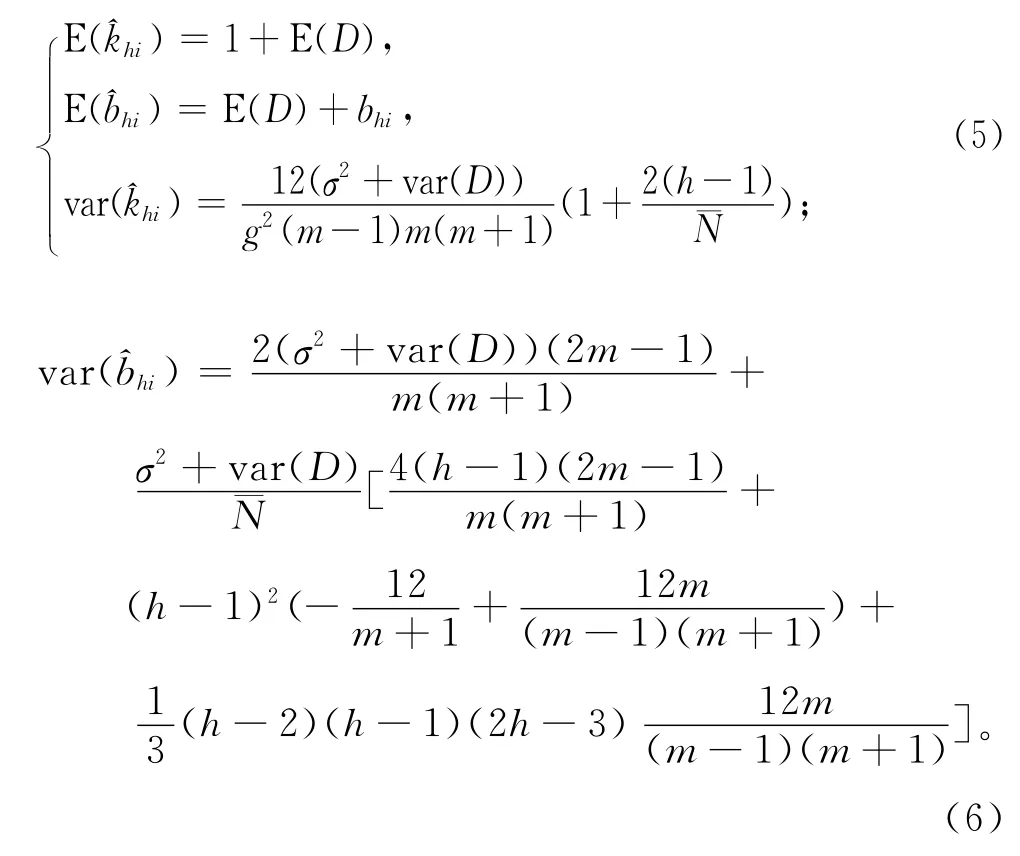
由式（5）、（6）可知，与频率偏移和时钟偏移的方差成反比，与延迟Di成反比，与阈值T成正比。延迟Di（信道争用）和T对（同步精度）有制约的关系，即随T和Di变化而变化。为了避免产生信道争用，需要仿真验证确定Di和T值，保证算法的同步精度。

1.2 算法实现

参考节点对其覆盖区域内的节点广播式发送脉冲，接收到同步脉冲的节点记录下次脉冲到达时间，根据图2对时间数据进行处理。

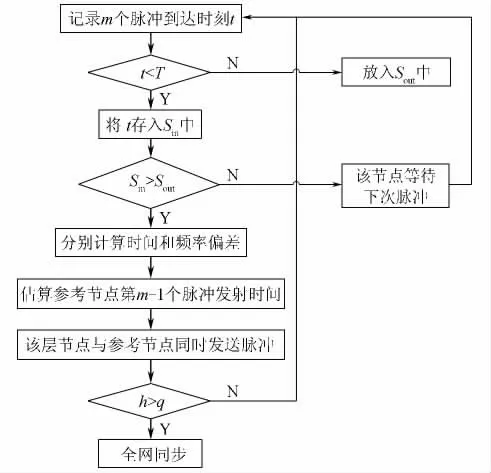
图2 自适应协作时间同步协议接收方处理流程图Fig.2 The flow chart of the receiver in the adaptive cooperative time synchronization protocol

网络中接收到脉冲的节点需要对脉冲信号进行处理，如图2所示，直至全网节点实现同步。在图2中，比较Sout和Sin，若Sout＞Sin，则该节点本次不需估算下次脉冲发送的时间，2个周期发送一次同步脉冲；反之，若Sout＜Sin，该节点每一个同步周期发送一次脉冲。

1.3 能耗分析

在中继模型中，假设节点1到节点2距离为d，节点1到节点M距离为βd，其中0＜β＜1，在自由空间路径损耗模型下，所有节点的最低接收功率均为Pr，根据文献［11］，发射功率为：

k＝（4π）2／（Glλ2）可视为常数。由式（7）可知，发射功率与收发双方之间距离d的平方成正比。若在其他传播模型中，发射功率随距离d上升的速度更快。

1）不存在中继节点M，节点1与节点2通信，发射功率为

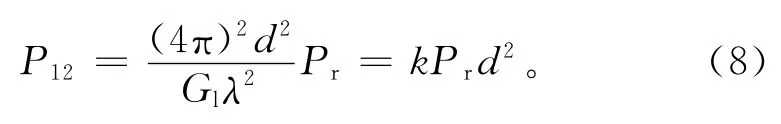
2）存在中继节点M，节点1与节点2通信，发射功 率为P1M和P2M：

根据式（8）、（9）和（10）可知，引入中继节点后，脉冲传播距离相同，降低发射功率倍数为

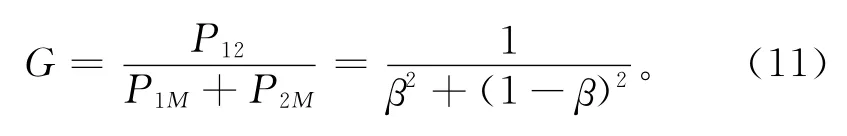
对式（11）求导，降低发射功率倍数最大值为Gmax＝2。

在网络通信中，发射脉冲通常比接收脉冲消耗更多的能量，ATCTS算法一方面通过中继节点使发射功率降低了G倍，另一方面为了降低信道争用率，减小节点发射脉冲的频率，从而节约能量，降低了能耗。

在CTS算法中，假定有q层网络，每层有N个节点，参考节点广播k次同步脉冲后，CTS算法的同步开销可表示为：

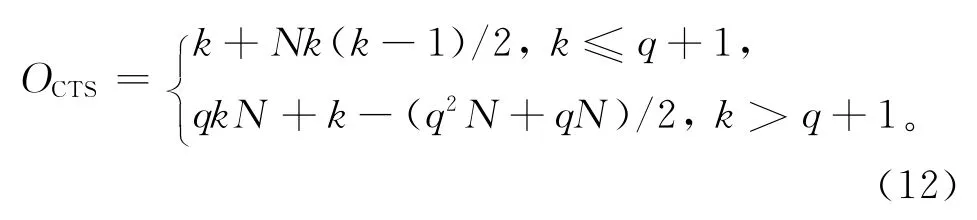
由式（12）不难发现，算法的同步开销与每层节点个数N成正比。在CTS算法中，N值越大，同步性能越好，但却产生了信道争用，影响同步精度；而ATCTS算法根据式（5）和（6），选取Di和T，在不降低CTS算法同步精度的前提下，减小节点发射脉冲的次数，即NATCTS＜NCTS，故ATCTS算法的同步开销低于CTS算法。

2 仿真与分析

2.1 同步性能分析

为了验证ACTS算法的性能，对算法中的时间偏移和频率偏移2个参数进行数值仿真。仿真条件：在半径为100 m的圆形区域内随机布置1000个节点，节点1在圆心位置，传输半径为R。网络共8层，脉冲间隔时间g＝2s，同步序列脉冲个数m＝5。为了便于仿真，设节点的频率偏差ki＝｜Ai｜，Ai～Ν（1，0.001）。对ATCTS和CTS算法同步参数进行1000次的仿真结果如图3所示。

图3 （a）和（b）分别为ATCTS算法与CTS算法频率偏差和时间偏差的对比曲线。T1＝0.2的同步精度明显低于T2＝0.4时的同步精度，T值增加，N－就增加，则ATCTS算法的同步精度提高，与理论相符；当T2＝0.4，延迟D满足D～Ν（0.11，0.004）时，ATCTS算法同步性能接近于CTS算法同步性能。

2.2 同步开销分析

图4为ATCTS算法与CTS算法同步开销影响的对比曲线。

图4 参考节点脉冲发射对同步开销的影响Fig.4 The influence of the sending pulse of reference node on the synchronization overhead

从图3、4可见，自适应阈值处理同步算法在不降低协作同步算法同步性能的条件下，同步开销明显低于CTS算法。由于协作同步算法中的参考节点每广播一次同步脉冲，接收到脉冲的所有节点将之前接收到的脉冲发送出去，随着接收到脉冲的节点数目增加，产生信道争用；而自适应阈值处理同步算法通过减小节点发送脉冲的频率，既减小了算法发送消息的数量，又降低了信道争用率。

2.3 节点能量效率分析

在协作同步中，远方节点可直接接收到节点1的同步脉冲，中间节点起协作作用，不会出现同步误差累积。利用中继节点，缩短脉冲的传播距离以提高能量效率。图5为中继节点位置和能量效率提高倍数对节点能量效率影响的仿真曲线。

从图5可见，当中继节点处于收发节点距离中心处，发送节点的发射功率仅为原来的1／2。

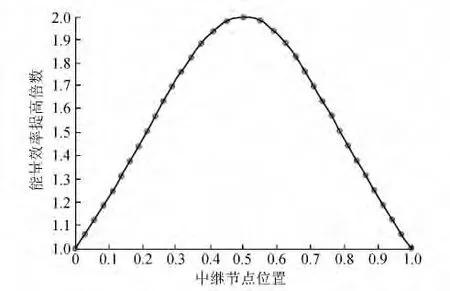
图5 中继节点位置对节点能量效率的影响Fig.5 The influence of the relay node’s location on the energy efficiency

3 结束语

利用空间平均，解决了分层或分簇同步协议中出现的误差累积，提高了同步精度；利用随机延迟和自适应阈值处理，减小脉冲的发送频率，降低了信道争用和能量消耗；引入协作中继，提高了算法的能量效率；节点执行相同的同步算法，具有良好的可扩展性和算法鲁棒性。从仿真结果可看出，确定阈值时间和延迟后，本算法在不降低同步精度的情况下，同步开销优于原算法。

［1］Ganeriwal S，Kumar R，Srivastava M B.Timing－sync protocol for sensor networks［C］／／Proceedings of the 1st International Conference on Embedded Networked Sensor Systems.ACM，2003：138－149.

［2］Maróti M，Kusy B，Simon G，et al.The flooding time synchronization protocol［C］／／Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems.ACM，2004：9－49.

［3］Kim B K，HongS H，Hur K，et al.Energy－efficient and rapid time synchronization for wireless sensor networks［J］.IEEE Transactions on Consumer Electronics，2010，56（4）：2258－2266.

［4］Zhang X，Hu G，Xu N，et al.Cooperative time synchronization based on industrial wireless networks［C］／／2nd International Conference on Advanced Computer Control.IEEE，2010：310－314.

［5］Hu An－swol.Time synchronization in large－scale natwork［D］.New York：Cornell University，2007：77－80.

［6］Werner－Allen G，Tewari G，Patel A，et al.Firefly－inspired sensor network synchronicity with realistic radio effects［C］／／Proceedings of the 3rd International Conference on Embedded Networked Sensor Systems.ACM，2005：142－153.

［7］Sun Y，Jiang Q，Zhang K.A clustering scheme for Reach－back Firefly Synchronicity in wireless sensor networks［C］／／3rd IEEE International Conference on Network Infrastructure and Digital Content，2012：27－31.

［8］金虎.无线传感器网络中一种自适应时间同步算法［J］.黑龙江大学工程学报，2012，3（1）：111－114.

［9］薛琴.一种无线传感器网络的协作时间同步方法［J］.无线通信技术，2012，21（4）.

［10］Serpedin E，Chaudhari Q M.Synchronization in Wireless Sensor Networks：Parameter Estimation，Performance Benchmarks，and Protocols［M］.Cambridge：Cambridge University Press，2009：89－92.

［11］Rappaport T S.Wireless Communications：Principles and Practice［M］.New Jersey：Prentice Hall PTR，2012：45－65.