基于压缩感知和WSNs 的井下应急语音通信系统设计*

苗曙光，李淮江，刘晓文

(1.中国矿业大学 信息与电气工程学院，江苏 徐州221008;2.淮北师范大学 物理与电子信息学院，安徽 淮北235000;3.中国矿业大学 物联网(感知矿山)研究中心，江苏 徐州221008)

0 引 言

现有的煤矿语音通信系统主要是调度电话和井下小灵通等方式，一旦发生矿难(如矿震、塌方事故等)，依靠于传统有线的调度电话将处于瘫痪状态，无线基站无法工作。但是依赖于多跳自组织网络的无线语音传感器网络可以依然工作，救援人员通过钻孔，放置信标节点，利用传感器网络的自愈性能，建立与井下节点的通信，开始和被困矿工语音通信，保障营救工作快速有序的展开［1］。所以，建立一套不依赖于主干网络和独立供电的无线传感器网络(WSNs)煤矿井下应急语音通信系统具有重要意义。

压缩感知(compressive sensing or compressive sampling)采用随机采样的方法，具有较低的计算复杂度、高压缩比、较好的语音重构质量的特点，非常适合应用在能量和带宽都受限无线多媒体语音传感网络。文献［2］提出了一种传感器节点上实现声音信号的压缩感知方法，将传统的采样频率降低至1/5。文献［3］将压缩感知的方法应用于语音和音频信号的处理，并且证明其优越性。文献［4］首次将压缩感知的方法应用于矿井语音通信，但是缺少对井下语音特点和传输环境特点论述。虽然压缩感知应用研究取得一定成果，但是在煤矿井下的应用才刚刚起步。

煤矿井下无线信道受限，能量受限，信息传输具有不对称性，传输距离长，需要多跳传输。考虑到煤矿井下巷道复杂的环境特点，本文提出了一种基于压缩感知和WSNs 的井下应急语音通信系统。对比实验表明:CoSaMP 重构效果好，通信距离为20 m 时，可以可靠地实现井下应急语言通信。

1 基于WSNs 的语音传感器网络结构

网络结构如图1 所示，系统包括语音节点、中继路由节点、Sink 节点，以及有线网络。语音节点将采集到的声音信号通过多跳转发和中继路由节点，传给处理能力相对较强的Sink 节点，该节点可以直接对语音进行重构解码，也可以直接将压缩的语音数据包通过CAN 总线传输到上位机进行解码播放。

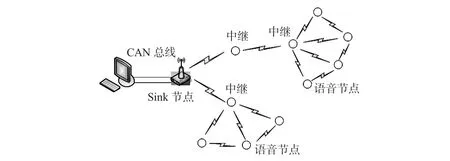
图1 语音传感器网络结构Fig 1 Structure of voice sensor networks

2 压缩感知的基础理论

文献Candes E［5］和Donoho D L［6］，在2006 年提出的压缩感知指出，只要信号是可压缩的或者在某个变换域是稀疏的，就可以用一个与变换基不相关的观测矩阵将变换所得的高维信号投影到一个低维空间上，然后通过求解一个优化问题就可以从这些少量的投影中以高概率重构原始信号。在该理论框架下，采样速率不依赖于信号的带宽，而决定于信息在信号中的结构和内容。这种新的采样理论突破了奈奎斯特采样定理的限制，被美国科技评论评为2007 年度十大科技进展。

2.1 压缩感知理论框架

压缩感知理论指出，设长度为N 的信号X 在某组正交基或紧致框架Ψ 上是稀疏的，其稀疏度为K(K≪N)，稀疏度为K 指X 本身有K 个非零元素，或者在某个变化域(如傅里叶变换或小波变换)Ψ 内的展开系数有K 个非零元素。如果用一个与变换基Ψ 不相关的观测矩阵ΦM×N(M≪N)对系数向量进行线性变换，并得到观测向量Y:M×1，那么就可以从观测集合中精确或高概率的重建原始信号X［5，6］。

信号在观测向量上的投影可以表示为

其中，yi为压缩感知获取的M 个采样值，由组成的观测基Φ 与变换基Ψ 不相关，应满足定义1。

定义1 观测矩阵Φ 和变换基Ψ 两者的相干度定义为

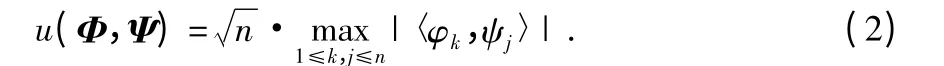
相干度测量Φ 和Ψ 中任意两个元素的最大相关性。如果Φ 和Ψ 包含相关元素相干度就很大;否则，就很小，满足

重构信号的关键是找出信号x 在Ψ 域中的稀疏表示，可以通过l0范数优化问题找到具有稀疏结构的解

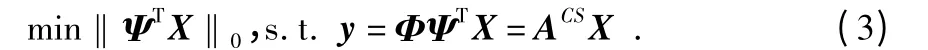
由于上式的优化问题是一个难求解的NP－hard 问题，所以可以用l1约束取代l0约束

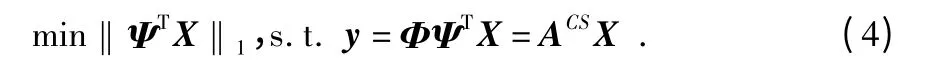
其中，Φ 需要满足约束等距准则(RIP)，即:

定义2 (约束等距准则RIP)对于每个整数S=1，2，…，N，定义矩阵A 的等距常量δS作为满足下式最小数

对于所有稀疏的S 稀疏向量x 都满足。约束等距性等价描述:矩阵A 的所有S 列子集都近似正交。

在感知矩阵满足RIP 的前提下，如果精确重建K 稀疏信号X，测量次数M 需要满足

2.2 压缩感知井下语音WSNs 框架

基于压缩感知的井下WSNs 应急语音通信，充分利用了压缩感知的两个特点:1)采样即压缩，计算复杂度低，对存储要求较低，适合能量和计算能力有限的WSNs 节点;2)语音压缩比高，适合带宽受限的无线传感器传输，同时满足实时性高，降低能耗的目的。另外，压缩感知将传统的(语音采样压缩编码传输到接收解码播放的语音通信)对称式计算模式转变为非对称计算模式，如图2 所示。

图2 语音压缩感知框架Fig 2 Frame of voice compressive sensing

系统工作的过程分为三步:首先，求出语音信号在变换域的稀疏表示，其次，设计一个平稳的与变换基Ψ 不相关的观测矩阵Φ，对信号X 进行随机采样，并进行无线传输;最后设计重构算法，从线性测量Y 中恢复原始语音信号并播放。

2.3 压缩传感设计

本文采用如图3 所示的改进方法，进行随机压缩采样并传输。将随机降维处理，转移到后端具有融合处理能力较强的终端进行，极大地减少采集节点的开销，降低能耗，延长网络周期［2，3］。

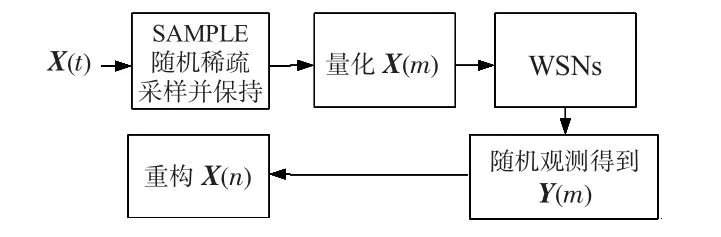
图3 压缩感知实现过程Fig 3 Realization process of compressive sensing

图3 实现的核心思想是:首先，设计SAMPLE 随机采样矩阵，采集M 个观测值X(m)，直接数字量化，然后通过WSNs 发送到功能较强的汇聚节点;然后，在接收端进行随机降维观测得到观测向量Y(m);最后对观测向量进行快速优化重构，得到原始信号的近似估计。

3 语音压缩感知的重构算法

基于压缩感知方法的WSNs 的语音通信系统，将语音传感器采集节点的计算复杂度巧妙地转移到了处理能力和能量较强的接收端，所以，如何选择设计快速重构算法至关重要。

目前为止，出现的重构算法大致可以分为三类:凸优化方法、贪婪算法和组合算法。研究可知，这三类算法各有优缺点:凸优化方法重构所需的观测次数最少，但往往计算负担很重;贪婪追踪算法在运行时间和采样效率上都位于另外两类算法之间。所以，本文以贪婪算法——OMP 和Co－SaMP 算法进行仿真重构，仿真测试验证本文设计方法的有效性［8］。

4 实验仿真分析

本文实验基于Matlab 平台对截取的一段语音进行仿真验证，语音原始数据采用8 kHz 采样，采样精度16 bit。

1)如图4 所示，采用OMP 算法对该段语音数据进行随机采样和重构，观测率M/N=0.3。

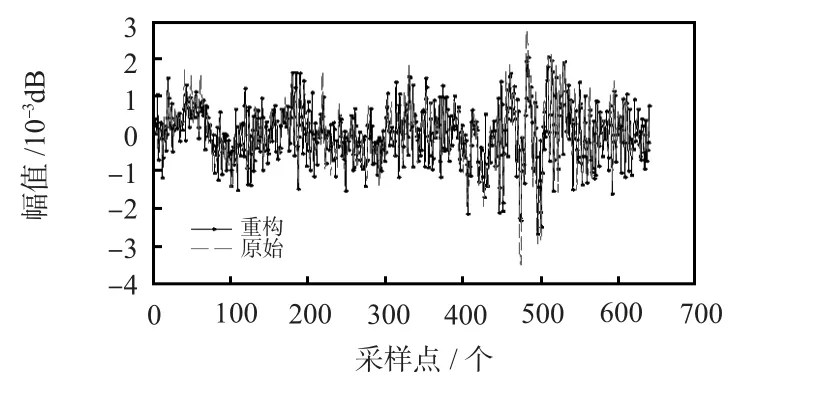
图4 OMP 算法重构结果Fig 4 Reconstruction result of OMP algorithm

仿真结果能够较好的重构原始信号，通过wavwrite(z1，8000，16，‘output.wav’)恢复重构语音文件output.wav，采用MOS(5 个等级打分机制)10 人平均评分MOS=4.52，可以到达语音不失真，可懂级别。采用OMP 算法仿真时间消耗T=0.24 s，SNR=－0.198 6 dB。重构误差re=1.023 1%。一般来说，定义重构信号和原始信号误差的欧式范数和原始信号的范数之比小于1%为信号高概率重构，即，其中，为重构信号，x 为原始信号。

2)如图5 是采用CoSaMP 算法进行重构的波形。同样选择观测比为0.3。从仿真结果可以得出:T=0.2 s，SNR=－0.1501 dB，重构误差re=1.0091%，总体优于OMP 算法。

图5 CoSaMP 算法重构结果Fig 5 Reconstruction result of CoSaMP algorithm

3)由于井下环境特殊，噪声干扰较大。图6 给出M/N=0.59，随着SNR 增加情况下，OMP 和CoSaMP 算法性能比较分析。

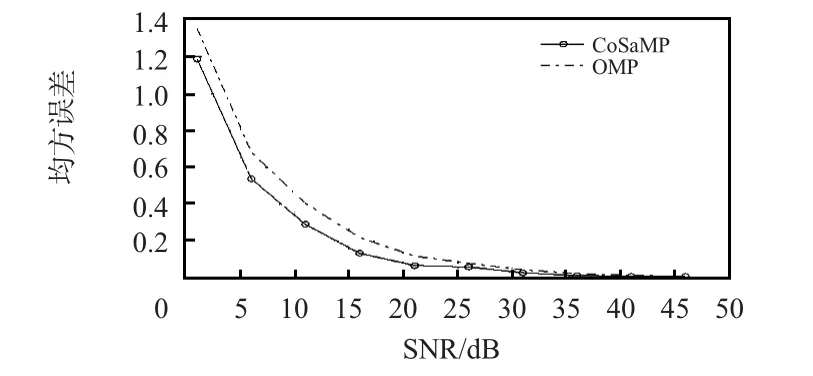
图6 OMP 和CoSaMP 算法性能比较Fig 6 Performance comparison between OMP and CoSaMP algorithms

从仿真结果来看，当观测率为0.59 时，CoSaMP 和OMP 算法均呈现随着信噪比增大重构误差减小的趋势，但是CoSaMP算法性能明显优于后者。通过分析，本文设计的基于WSNs的应急语音系统选择CoSaMP 算法作为语音重构算法。

4)由于井下环境属于有限异质空间，传感器节点通信距离远小于地面环境，需要充分考虑节点在井下的通信半径，因此，在煤矿井下进行2.4 G 无线通信实验实际测试，得到两个传感器节点RSSI 变化和收包率如图7 所示。

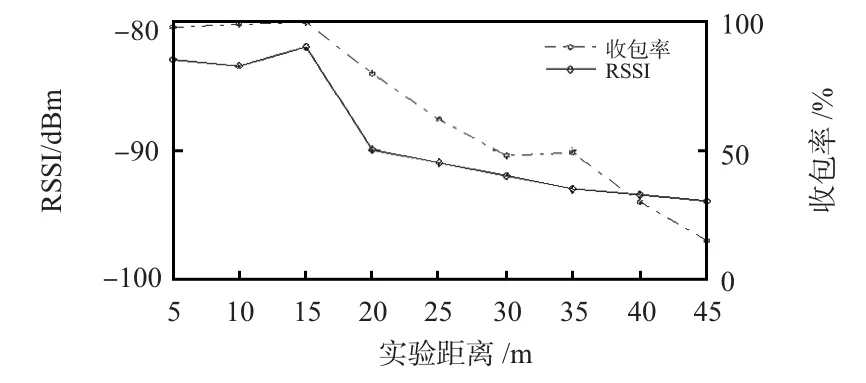
图7 RSSI 和收包率随距离的变化Fig 7 Variation of RSSI and packet receiving rate with distance

通过图7 可以看出:RSSI 和收包率随距离的增大而减小。在20 m 通信距离内，收包率达到90%，RSSI 值在－90 dBm，但30 m 时已经大大减小到55%和－93 dBm，不能满足矿井通信的要求。在建立网络的时候，两个节点的距离应小于20 m，本设计的节点距离设置为20 m。

5 结 论

本文根据压缩感知的相关理论，提出了一种新的基于压缩感知的井下无线应急语音通信网络。主要设计思想是利用压缩感知的方法，实现采样即压缩，把复杂的语音压缩编码简化，缓解采集节点的开销，把复杂的计算转移到功能较强大的汇聚节点或者上位机，使井下无线多媒体语音传感器网络成为可能。通过对比仿真实验证明了采用CoSaMP 重构算法的优越性。本文提出的方法，可为矿井无线应急语音通信提供了一种新设计的思路，值得进一步研究。

［1］ 刘晓文，苗曙光，杜存功，等.基于WSNs 的井下应急语音通信系统的研究［J］.传感器与微系统，2010，29(1):15－17.

［2］ 王 泉，吕方旭，张金成.基于CC2530 的声音信号压缩感知硬件实现方法［J］.计算机工程与设计，2014(7):2356－2359，2446.

［3］ 余 恺，李元实，王 智，等.基于压缩感知的新型声信号采集方法［J］.仪器仪表学报，2012(1):105－112.

［4］ 马丽娜，曹新德.基于压缩感知的煤矿井下语音通信系统［J］.安徽理工大学学报:自然科学版，2011(3):72－74.

［5］ Candes E.Compressive sampling［J］.IEEE Transactions on Information Theory，2006，52(4):1433－1452.

［6］ Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289－1306.

［7］ 杨海蓉，张 成，丁大为，等.压缩传感理论与重构算法［J］.电子学报，2011(1):142－148.