O型橡胶圈动密封结构的有限元分析
郭丽霞 关静岩


摘 要:建立深海旋转轴O型橡胶圈动密封结构三维模型,采用ABAQUS /Explicit非线性有限元方法计算了O型橡胶圈在工作水压和工作转速下的接触压力。通过这些研究,确定了O型橡胶圈接触压力的分布规律,分析了水压和工作转速等典型参数对密封性能的影响。
关键词:接触压力;温度;密封;O型橡胶圈
中图分类号:TB42 文献标识码:A DOI:10.15913/j.cnki.kjycx.2015.03.019
在早期,国内报道的深海旋转轴密封主要是从承压型密封方面来考虑的。1982年,我国的张训义就提出了深海动态密封,主要是分析O型密封圈在深海环境下1 000 m内的往复运动、旋转运动和振荡运动的动态密封情况;1993年,国内学者从材料的选择、结构特点和经济效益等方面报道了机械密封在水下机器人中的应用;1994年,美国报道了一种用于深海旋转轴的双重密封专利。
深海承压型密封相当于常压环境中使用的高压密封,它的不同之处在于,常压下的高压密封一般可以防止流体从设备内部向外部泄漏,而深海密封是防止外部流体沿密封件进入设备内部,并且其允许的泄漏量很小。
推进系统的主要功能是为水下装备的航行提供所需要的推进动力,其密封的可靠性直接影响装备作战任务的完成。针对推进系统无润滑密封问题,应用可靠性技术、材料学、动密封技术和磨损理论等,分析了该系统的动态特性和失效机理,并建立系统有限元模型,用于研究不同载荷和环境条件下系统密封件的变形情况和密封特性。
1 计算模型
1.1 橡胶材料的本构关系
橡胶是一种各向同性、可高度变形、高弹性和压缩性较小的材料,其不仅具有类似于金属材料的弹性,还具有类似于黏性液体吸收能量的性质。同时,由于橡胶材料的特性非常复杂,其材料和几何特性均呈非线性变化,在实际应用中,往往还存在着边界条件复杂和接触非线性等问题。所以,橡胶结构的有限元分析属于非线性有限元范畴,其非线性突出地表现在以下3方面:①橡胶材料的应力应变关系是一个非常复杂的非线性函数,用应变能函数表示;②橡胶在力的作用下,一般伴随着大位移、大应变,其应变位移关系也是非线性函数;③密封计算的边界条件非常复杂,必须包含接触面的受力计算,呈非线性关系。
对于橡胶应变能函数,一般采用穆尼-瑞林(Mooney-Rivlin)模型来描述,其函数表达式为:
W=C1(I1-3)+C2(I2-3). (1)
式(1)中:W为应变能密度;C1,C2为材料Mooney-Rivlin系数;I1,I2为第一、第二应变张量不变量。
本文中,C1,C2分别为1.87,0.47.
1.2 有限元模型建立
根据密封系统的结构特点、密封件实际尺寸和沟槽尺寸,建立具有刚柔接触的密封系统有限元模型,如图1所示。密封件的材料为橡胶材料,近似为不可压缩超弹性体,密封套固定约束,密封套和外轴均与橡胶圈接触。
对此模型进行网格划分,其结果如图2所示。图2中,模型全部采用六面体单元,并且在外轴外侧划分4层较密网格。这是因为这部分单元与密封圈、密封套接触,存在应变,而外轴内部几乎不存在变形。
2 工作水压和工作转速对密封性的影响
2.1 O型橡胶圈密封工作原理
O型橡胶圈是一种挤压型密封。挤压型密封的基本工作原理是依靠密封件发生弹性变形,在密封接触面上造成接触压力,接触压力大于被密封介质的内压,则不发生泄漏;反之,则发生泄漏。在动密封系统中,O型橡胶圈与外轴、密封套有3个接触面,如图3所示。根据O型橡胶圈的密封工作原理,3处接触面的接触压力皆大于工作水压时,才能达到密封效果。因此,在以下的分析中,分别计算、分析了O型橡胶圈3个接触面在指定工作水压和工作转速下的接触压力,并判定O型橡胶圈是否可以达到密封效果,进而确定工作水压和工作转速对O型橡胶圈密封性能的影响。
2.2 工作水压
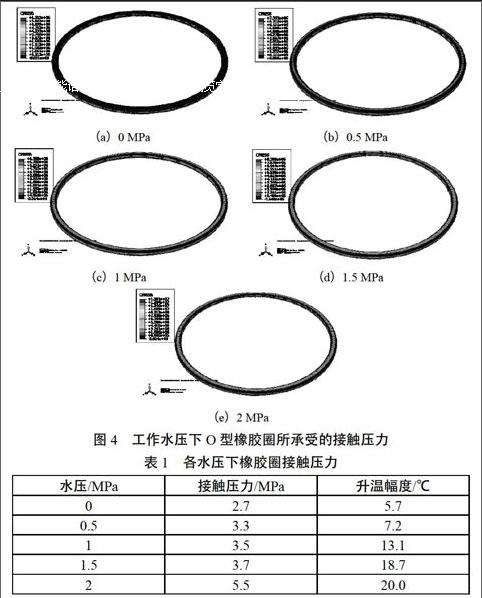
在此次分析中,分别在水压为0 MPa、0.5 MPa、1 MPa、1.5 MPa、2 MPa时分析动密封系统,并得出在各水压下O型橡胶圈所承受的接触压力,如图4所示。
从图4的分析结果中可以看出,当水压为0 MPa、0.5 MPa时,只有Ⅰ、Ⅲ接触面上的接触压力较为明显。随着水压的增大,在水压达到1 MPa后,Ⅱ接触面上的接触压力逐渐明显且趋于稳定,各水压下O型橡胶圈所承受的接触压力也是在不断增大的。至于接触压力不均,则是因为在外轴运动的过程中,所产生的波动可能会导致接触压力的受力不均,并且橡胶圈的爬行可能会加剧这种情况的发生而引起的。但是,这种情况只是瞬间发生的,因此,其平均接触压力即可用来判定其密封性能。经过计算,各水压下其平均接触压力均大于其计算水压,如表1所示,满足密封的要求。为了更严谨的定义工作水压对O型橡胶圈密封性能的影响,下面简要分析各水压下橡胶圈的温升情况,其结果如表1所示。从其计算数据中可以看出,随着水压的增大,橡胶圈的升温幅度在不断加大,并且加速了橡胶圈的老化速度。因此,用工作水压来增强橡胶圈的密封性能仅限定在一定的水压下。
2.3 工作转速
在此次分析中,分别在转速V=0 r/min、191.5 r/min、383 r/min、574.5 r/min、766 r/min时分析动密封系统,并得出在各转速下O型橡胶圈所承受的接触压力,如图5所示。
从图5的分析结果中可以看出,各转速下O型橡胶圈的接触面大致相同。这主要是因为在加载转速前已经加载了水压,并且各转速下水压恒定。同时,从图5中的数据中可以看出,橡胶圈在各转速下所承受的接触压力变化不大,这点也可以从其平均接触压力上看出,如表2所示。由此可见,在工作过程中,O型橡胶圈所承受的接触压力主要与工作水压有关,而工作转速对O型橡胶圈所承受的接触压力影响不大。
橡胶圈的密封性能还受橡胶老化问题的限制。为了进一步说明转速对橡胶圈密封性能的影响,分析其在各转速下的温升情况,其结果详见表2. 从表2中的数据中可以看出,随着转速的不断加大,橡胶圈升温幅度也在不断提高,从而加速了橡胶圈的老化速度,损害橡胶圈的密封性能,降低其使用寿命。
3 结论
从O型橡胶圈在不同工作水压和工作转速的分析结果中可以看出,当只考虑接触压力这一密封性能指标时,增大工作水压可以提高密封性能,而增大转速则对接触压力的影响不大。同时,考虑到温度变化对橡胶老化的影响,计算了橡胶圈在不同工作水压和工作转速下的升温幅度。分析结果表明,工作水压和工作转速都会导致橡胶圈温度升高,加速橡胶圈的老化速度。因此,如何降低橡胶圈在工作过程中的升温问题还有待进一步研究。
参考文献
[1]任全彬.橡胶O型圈的变形及应力分析[J].航空动力学报,1995,10(3):241-244.
[2]赵忠丽.橡胶密封制品的有限元模拟与结构优化[D].青岛:青岛科技大学,2006.
[3]李建国,丁玉梅,杨卫民,等.油封密封性能的有限元分析[J].润滑与密封,2006(10):116-119.
[4]胡殿印,王荣桥,任全彬.橡胶O型圈密封结构的有限元分析[J].北京航空航天大学学报,2005(2):255-260.
[5]吴文涛,叶子波,黄兴.有限元分析法在工程密封件设计上的应用[J].润滑与密封,2007(11).
[6]陈庆,陈利强,康博.往复运动橡胶O型密封圈密封机制及其特性的研究[J].润滑与密封,2011(06).
〔编辑:白洁〕

