快速亚像素图像配准算法研究

戴宪策，刘昌锦



快速亚像素图像配准算法研究

戴宪策，刘昌锦

（新兴技术研究所，安徽 合肥 230031）

亚像素图像配准是图像配准技术中的研究热点。常用的亚像素配准算法是相位相关法与拟合方法的结合。针对该方法中存在的时间和精度不能同时达到最优的问题，提出了基于角度-平移信号频率估计的亚像素配准算法，利用相位相关中的交叉功率谱的角度信息构建出了角度-平移一维信号，运用DFT相位差分法准确估计出一维信号的频率，进而计算出图像间的亚像素平移量。通过在Matlab下仿真实验，验证了本文算法在时间和精度上均优于拟合法。

图像配准；亚像素；角度-平移信号；相位差分

0 引言

图像配准是将不同时间、不同传感器或不同环境下获取的同一场景的两幅或多幅图像进行匹配、叠加的过程，广泛应用于遥感、计算机视觉、图像融合、医学成像和环境检测等领域[1]。图像配准的目的是获取不同图像间的几何关系，如平移、旋转、缩放等，其中最常见的是图像间的平移。

当前，越来越多的应用领域如医学图像分析、三维重建、视觉定位等，都依赖高精度的图像配准，因此亚像素级图像配准成为图像分析的研究热点之一[2-3]。相位相关法[4]和拟合法的结合是较为常用的算法，但是该算法的计算精度和运行时间是一对矛盾，无法同时达到最优。本文针对这一问题，根据相位相关的原理，结合相位信息[5]和相位差分频率估计方法[6]，提出了一种亚像素图像配准算法。

1 相位相关配准原理

设1(,)和2(,)分别代表两幅大小为×图像，1(,)和2(,)是2幅图像对应的傅里叶变换。如果1(,)和2(,)之间存在如下平移关系：

2(,)＝1(－0,－0) (1)

式中：(0,0)表示两幅图像之间水平方向和垂直方向的平移。那么根据傅里叶变换的平移原理，1(,)和2(,)的关系如下：

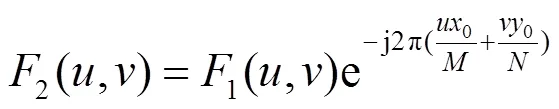
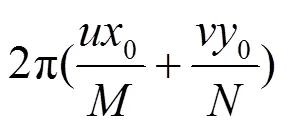
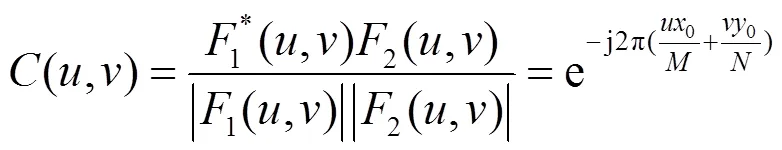
式中：1*(,)表示1(,)的共轭。交叉功率谱的傅里叶逆变换为：

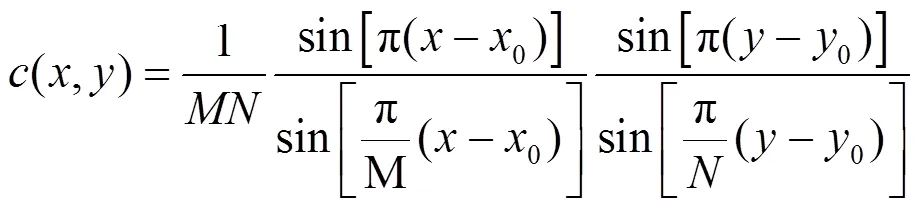
若(,)的值较大并且(0,0)为整数，(,)可以近似表示为脉冲函数：

通过寻找(,)中最大值的位置就可以确定两幅图像间的平移量。此即相位相关法配准的原理。

若(0,0)不为整数，通过相位相关法计算出的平移量将出现偏差。因此研究人员提出了多个提高配准精度的方法。其中常用的方法是拟合法，即利用多项式拟合(,)，计算多项式的极值确定亚像素位置。拟合法为了得到较为精确的位置，就必须采用更高阶的多项式，增加了计算的复杂度。

针对该方法中存在的问题，本文提出了新的算法，从交叉功率谱的角度信息中角度平移信号，估计信号的频率确定平移量。

2 改进算法原理

2.1 角度-平移信号构建

设D(,)表示交叉功率谱的角度，则：

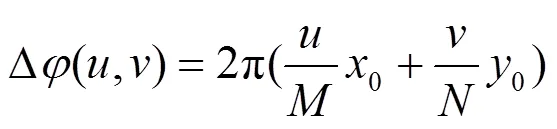
交叉功率谱的角度与其对应位置构成了平面方程函数，由于角度计算时的卷绕，实际得到的角度与位置关系的函数为：

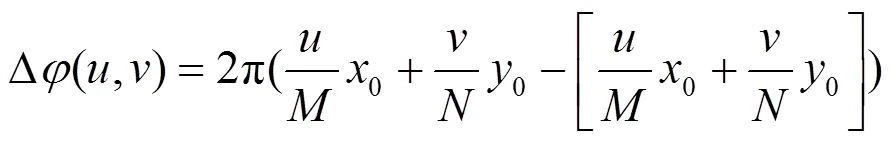
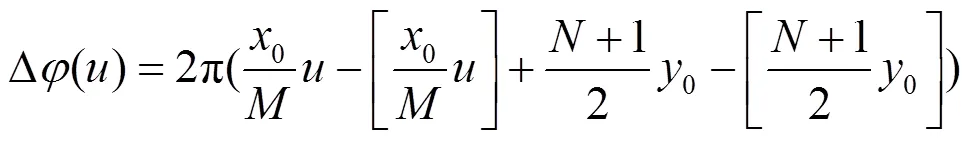
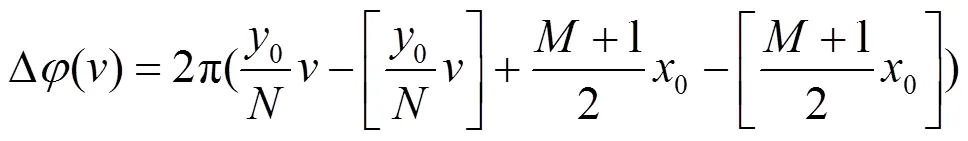
投影得到的角度函数均为周期函数，水平方向的周期为0/，垂直方向的周期为0/。由此构建了两个一维信号，分别计算信号的周期就能够得到两个方向的平移量。对信号进行傅里叶变换是计算其周期的一种方式，但是傅里叶变换的精度受限于信号测量时间长度，为了提高估计精度，本文采用相位差分的方法。

2.2 DFT相位差分

设某单一频率复正弦波信号的表达式为：

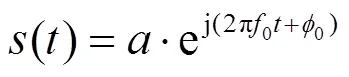
式中：、0和0为信号的幅度、频率和初相。对信号进行采样，设总采样时间为，总采样点数为。将采样序列分为长度相同的两个序列，分别设为1()和2()，则有：

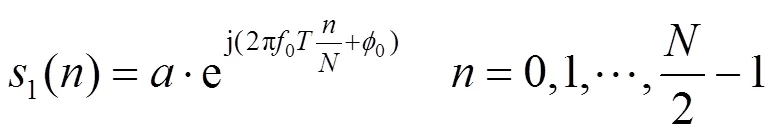
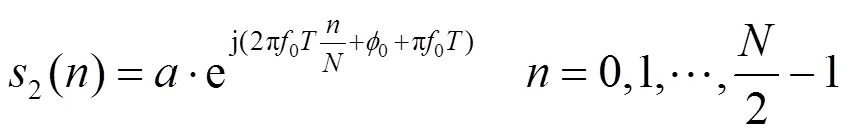
分别对1()和2()进行DFT，得到离散频谱1()和2()：

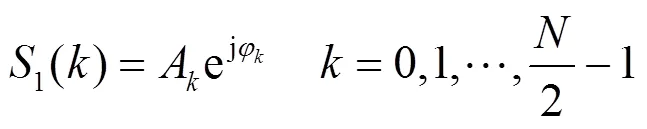
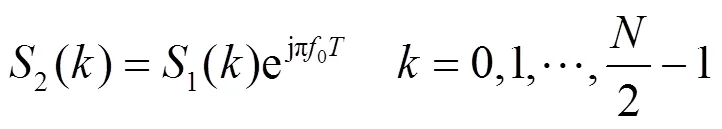
式中：A和分别为1()的幅度项和相位项：

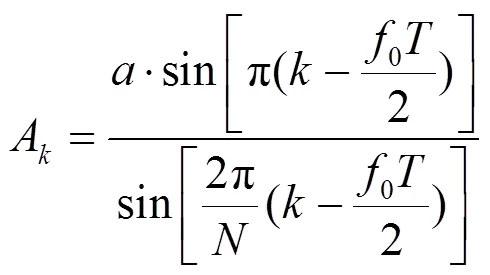
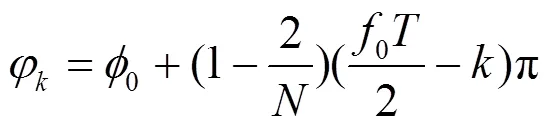
因此，1()和2()的幅度完全一样，最大幅度对应的离散频率是距离0/2最接近的整数，设为0。最大幅度对应的相位表示了0与0/2之间的偏差信息，由于初相未知，因此无法直接估计频率偏差。设1和2分别表示1()和2()最大幅度对应的相位，其相位差为：

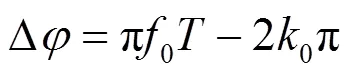
因此可以利用D估计频率偏差f：

f＝D/(p) (18)

最终计算得到的频率值为

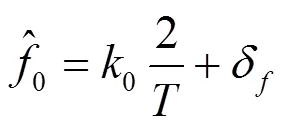
上述过程就是DFT相位差分法估计频率的原理。设构建的2个方向的信号频率分别为H和V，则两个方向的偏移量为：

0＝H(20)

0＝V(21)

2.3算法流程

根据2.1和2.2节中的分析，总结出算法流程如图1所示。

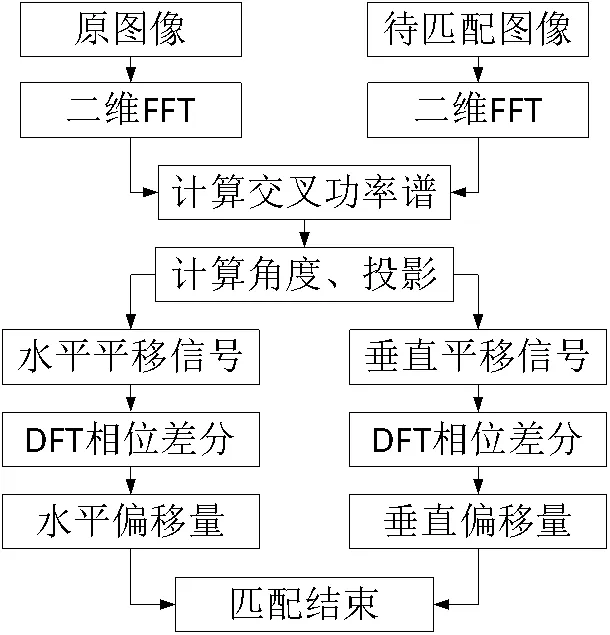
图1 算法流程图

首先计算两幅图像的交叉功率谱，再提取角度信息并投影到水平、垂直两个方向构建角度-平移信号，然后利用DFT相位差分估计频率，计算水平和垂直方向的偏移量。

3 算法测试

为验证算法的性能，本文设计了与拟合法的对比仿真实验。实验是在Windows 7，Matlab 8.1.0的平台上进行的，计算机主频为2.5GHz，内存为2G。实验使用的图像是经过平移、高斯模糊和降采样生成的。图2为实验采用的原始图像。

图2 原始图像

实验中，先将原始图像在水平和垂直方向上平移奇数个像素单位，再分别对原始图像和平移后的图像进行高斯滤波，然后对滤波后的图像进行2倍降采样，以此得到亚像素平移的图像。拟合法采用二元二次多项式拟合最大值附近5×5的邻域，对比指标分别为精度和运行时间。仿真实验的结果见表1。

从表1中可以看出，本文算法对比拟合法，不仅配准的结果更为准确，并且匹配时间也较少。实验验证了本文算法的优点。

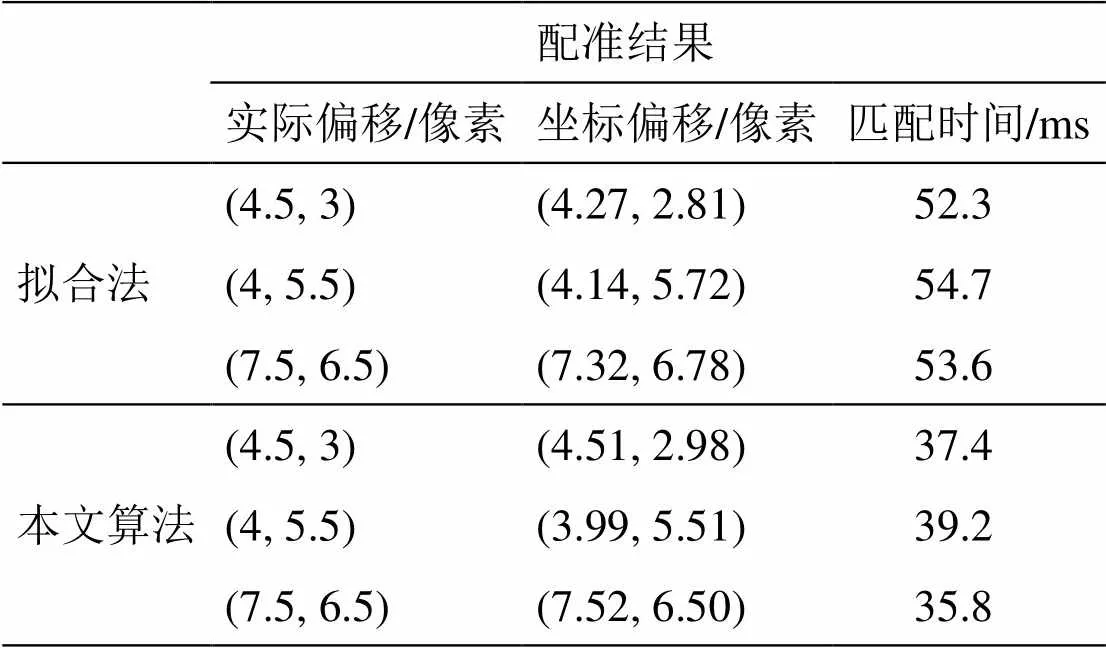
表1 仿真实验结果

4 结论

本文基于交叉功率谱的相位信息提出了一种新的亚像素配准算法，利用交叉功率谱的相位信息构建水平和垂直方向的角度-平移一维信号，采用DFT相位差分的方法准确估计一维信号的频率，进一步计算得出了水平和垂直方向的亚像素平移量。通过设计仿真实验，与拟合法计算亚像素平移的方法比较，本文提出的算法在时间和配准结果上均优于拟合法。下一步研究的方向是进一步提高配准的精度，同时缩短配准时间。

[1] 陈华旺, 马永龙. 一种基于相位相关的亚像素红外图像配准算法[J]. 光学与光电技术, 2013, 11(6): 15-18.

[2] 刘阁. 亚像素图像测量的研究[J]. 工程与试验, 2013, 53(4): 7-12+64.

[3] 陆凯, 李成金, 赵勋杰, 等. 一种快速的亚像素图像配准算法[J]. 红外技术, 2013, 35(1): 27-30.

[4] R C Gonzalez, R E Woods. 数字图像处理[M]. 2版, 北京: 电子工业出版社, 2010.

[5] Foroosh H, Zerubi A J, Berthod M. Extension of phase correlation to subpixel registration[J]., 2002, 11(3): 188-200.

[6] 齐国清, 贾欣乐. 基于DFT相位的正弦波频率和初相的高精度估计方法[J]. 电子学报, 2001, 29(9): 1164-1167.

[7] 王彩玲, 程勇, 赵春霞, 等.局部相位相关用于图像亚像素级配准技术研究[J]. 中国图像图形学报, 2011, 16(3): 427-432.

Research on Fast and Sub-pixel Image Registration Algorithm

DAI Xian-ce，LIU Chang-jin

(,230031,)

Sub-pixel image registration is a research hotspot in image registration. The combination of phase correlation and polynomial fitting is one of common algorithms. But time consuming and accuracy conflict in this algorithm. Aiming to this, a new algorithm based on frequency estimation of angle-offset signal is proposed. First, angle information of cross-power spectrum is used to form angle-offset signal. Then frequency of the signal is estimated accurately by phase difference of DFT. At last, sub-pixel offsets is computed. Experiments simulated under Matlab show that this algorithm is better than fitting both in time consuming and accuracy.

image registration，sub-pixel，angle-offset signal，phase difference

TP391.4

A

1001-8891(2015)04-0579-03

2015-01-09；

2015-02-16。

戴宪策（1990-），男，江苏徐州人，硕士研究生，研究方向为双目立体视觉。