基于组合积分系统的滤波

李娜，陈亮，任正云

（东华大学信息科学与技术学院，上海201620）

在信号采集过程中，由于外界干扰常常会在采集的数据中引入噪声，有时甚至会使信号发生失真，因此对于采集的大量数据往往需要进行滤波，去除干扰[1]。数字滤波器在语音信号处理、信号频谱分析、信号去噪及图像信号等各种信号处理中都有广泛的应用，无线脉冲响应（Infinite Impulse Response，IIR）滤波器与有限脉冲响应（Finite Impulse Response，FFR）滤波器[2]相比，具有相位结构简单、运算量小、经济高效的特点，并且可以用较少的阶数获得很高的选择性。

组合积分系统作为新型控制系统，广泛存在于工业生产中，组合积分环节本质上是一个均值滤波器，具有一定抑制噪声的能力。

本文在IIR数字滤波器算法基础上，设计基于组合积分系统的滤波算法，仿真实例表明：应用组合积分系统进行滤波，滤波参数固定、随机可调，与常用滤波方法相比具有明显优点。

1 IIR数字滤波器设计原理与方法

IIR数字滤波器传输函数的标准表达式（1）及对应的差分方程（2）为：

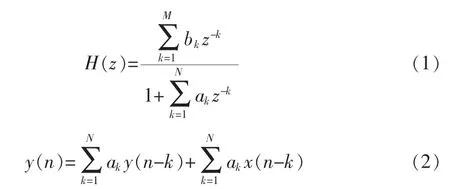
设计递归滤波器就是确定滤波器的系数ak、bk，使它满足滤波器的技术指标。

IIR滤波器的实现有多种结构，直接型、级联型、并联型及格型结构等。其中级联型较为容易实现且易于实现高阶滤波器，且任何高阶IIR滤波器都能表示成一阶和二阶的级联。

设计思路：根据任务确定数字滤波器的技术要求指标后，设计出与此性能相似的模拟滤波器，求出传递函数Ha（s），然后将Ha（s）按一定的方法转换成数字滤波器的系统函数。主要实现方法包括冲激响应不变法和双线性变换法。由于冲激响应不变法容易产生频率混叠现象，故多采用双线性变换法。

1.1 IIR数字滤波器的MATLAB实现

MATLAB信号处理工具箱实现IIR数字滤波器设计，流程图如图1所示。

文中采用巴特沃斯滤波器设计，MATLAB提供了估算滤波器阶数的函数，格式：[n，wn]=buttord（wp，ws，ap，as，‘s’），给定滤波器性能参数情况下，选择滤波器的最小阶数n。其中wp是通带频率，ws是阻带频率，ap是通带最大衰减系数，as是阻带最小衰减系数，“s”代表模拟滤波器。数字滤波器阶数估计时，wp和ws是归一化值，只能在[0，1]上取值。IIR数字滤波器的完全设计函数有Butter、cheby1、cheby2、ellip。这些工具函数既可用于设计模拟滤波器，也可适用于设计数字滤波器

图1 MATLAB实现IIR数字滤波器设计流程图Fig.1 MATLAB realization of IIR digital filter design flow

2 组合积分系统

在过程控制领域，存在很多带有时滞的积分系统，而一些带有大惯性环节的一阶过程也可以看成是积分过程[4-5]。在现代流程工业中，有许多过程是由多个不同的积分时滞项组成，但目前尚未引起人们的关注。蒸馏塔的底层过程具有传递函数k/s（1-2e-τ1s）e-τ2s，其是一个非最小相位时滞过程[6]。组合积分系统是一类新型的积分时滞过程系统，其传递函数由两个或多个积分时滞对象组成并可表示为如下形式：

Gi（s）是不含积分环节的稳定多项式，式k/s（1-e-τs）是包含在组合积分系统中的稳定的系统，时间延迟τ1i，τ2i必须满足等式：τ2i=τ2(i-1)+τ1(i-1)，1＜i＜n保证了过程的连续性。

2.1 组合积分环节本质

假设指数有界信号f（t），其变换为F（s），将其乘以组合积分环节g（s）:

得传输函数：

对式（4）求反变换可得：

式（6）右部可解释为对信号f（t）在长度为τ时间段[t-τ，t]上进行积分，对所得积分除以时间长度进行τ平均，相当于对信号f（t）在长度为τ时间段[t-τ，t]上进行的均值滤波算法。故式（4）所定义的组合积分环节等同于一个均值滤波器，与均值滤波器具有相同作用。均值滤波器是低通滤波器的一种特例，由此推出此组合积分环节为一个均值滤波器。

低通滤波器是数字滤波器的基础，高通及带通滤波器都可由低通滤波器转换实现。在设计基于组合积分系统滤波时可人为改变延迟时间的大小，便可控制参与均值滤波的项数。滤波器项数越大，低通滤波效果越好，滤去的高频分量越多。

2.2 组合积分环节方框图分析

用于滤波的组合积分系统滤波方框图如图2所示。

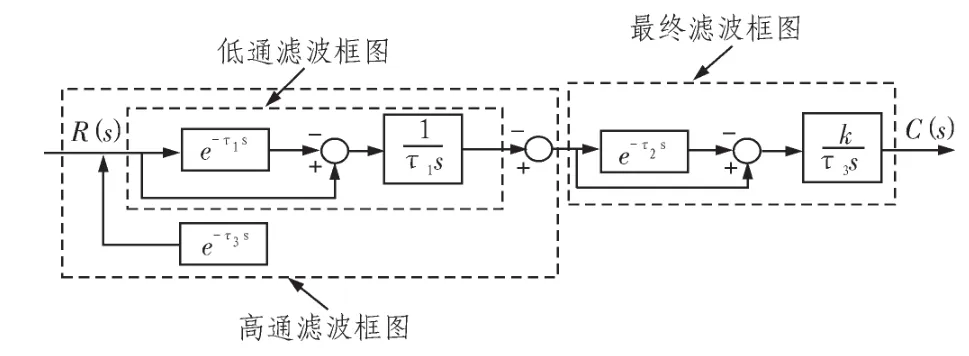
图2 组合积分系统滤波框图Fig.2 Block diagram of combined integral control system

传递函数为：

参数τ1控制参与均值滤波的项数，参数τ1，τ2共同控制高通滤波，参数K控制最后输出滤波与实际滤波的误差。

低通滤波环节传递函数为：

如式（6）推导知，此环节实现信号低通滤波的效果，时滞常数τ1可控，决定参与均值滤波的项数。τ1越大，低通滤波效果越好，滤去的高频分量越多，滤波后的信号越平滑。

高通传递函数为：

原信号通过延时环节不会改变原信号的频率，改变原信号的相位。而信号通过环节后只剩低频信号，即用原信号减去低频信号等同于高频滤波作用，故此环节实现的是高通滤波的作用。

最终滤波环节传递函数g′（s）为：

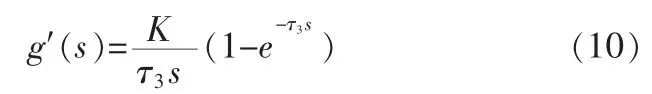
g′（s）作用等同于g1（s）将信号的频谱放大K倍，信号通过滤波环节之后会有衰减，放大倍，可减小信号与滤波信号的误差。高频滤波后信号通过此低频滤波环节，滤出高频环节后信号中相对的低频信号，信号达到了带通滤波的效果。

3 组合积分系统滤波计算机辅助设计

MATLAB信号处理工具箱的两个基本组成就是滤波器的设计和实现及频谱分析，工具箱提供了丰富而简单的设计，使原来繁琐的程序设计简化成函数的调用，特别是滤波器的表达方式和滤波器形式之间的相互转换显得十分简便，为滤波器的设计和实现开辟了一片广阔天地。

IIR滤波器目前最通用的方法是利用已成熟的模拟滤波器的设计方法来设计。IIR的设计都包括以下3个步骤：给出所需要的滤波器的技术指标；设计一个使其逼近所需要的技术指标；实现所设计的H（z）[6]。

3.1 Simulink仿真

Simulink仿真环境中建立组合积分系统模型，实现对信号动态的频谱分析。支持图形用户界面，并提供了许多自带的模块库，使建模过程像是垒积木一样简单易行。基于组合积分系统滤波系统模型图如图3所示。该仿真模型中共有5个示波器，示波器用来显示滤波后的时域响应。

滤波结果分别如图4～图7所示，由图4可以看出，滤波前时域波形比较杂乱，无法识别出信号周期；滤波之后无论是LP、HP、BP信号都特别稳定，滤波效果比较好。

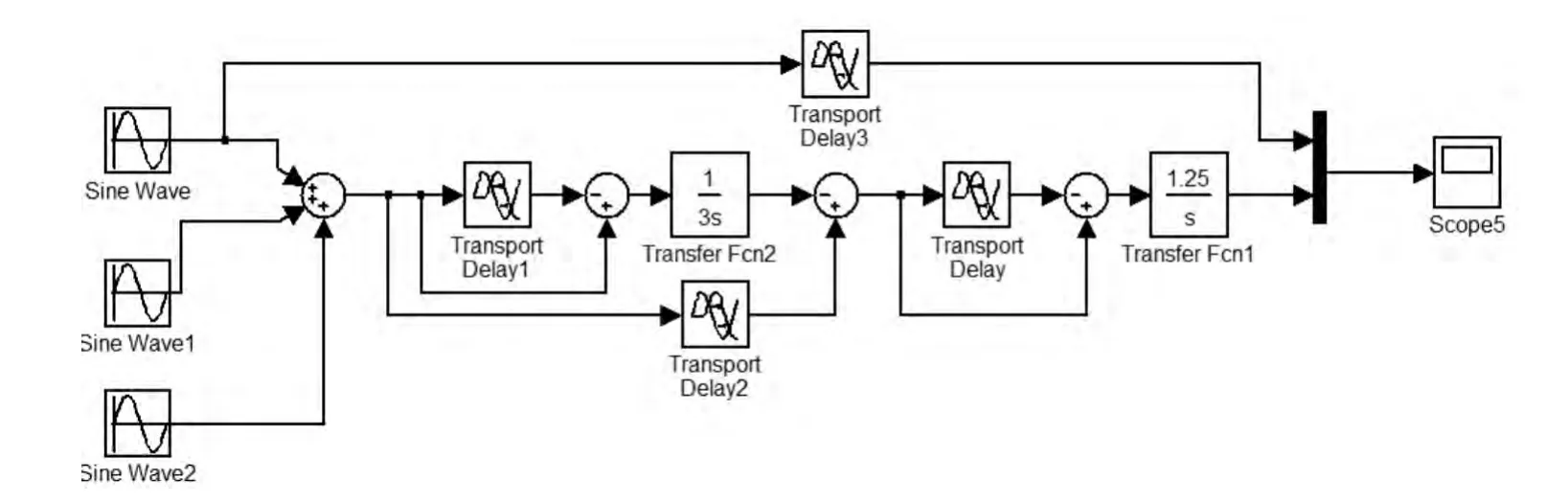
图3 基于组合积分系统滤波仿真模型Fig.3 Combined integrating control system simulation model

图4 复合信号时域波形Fig.4 Time-domain waveform before filtering

图6 高通滤波后信号时域波形Fig.6 Time-domain waveform of the HP filtered signal

图5 低通滤波信号时域波形Fig.5 Time-domain waveform of the LP filtered signal

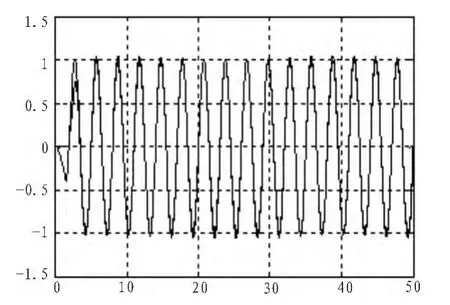
图7 信号对比时域波形Fig.7 Comparison of time domain response

3.2 滤波算法分析

图4和图5分别为巴特沃斯低通和高通滤波后信号的时域响应。滤波器前信号中有0.03 Hz、0.3 Hz、1 Hz共3个信号频率，图4滤波后只剩下0.03 Hz信号频率，其他高于0.03 Hz的频率信号已经被滤除。图5滤波后只剩下0.3 Hz和1 Hz共2个信号频率，其他低于0.3 Hz的频率信号已经被滤除。

采用基于组合积分系统滤波出的信号很稳定，只含有一种频率的信号，噪声少，信号平滑。IIR数字滤波器设计的巴特沃斯滤波程序，滤波后的信号中噪声较多，采用组合积分系统滤波效果较好。

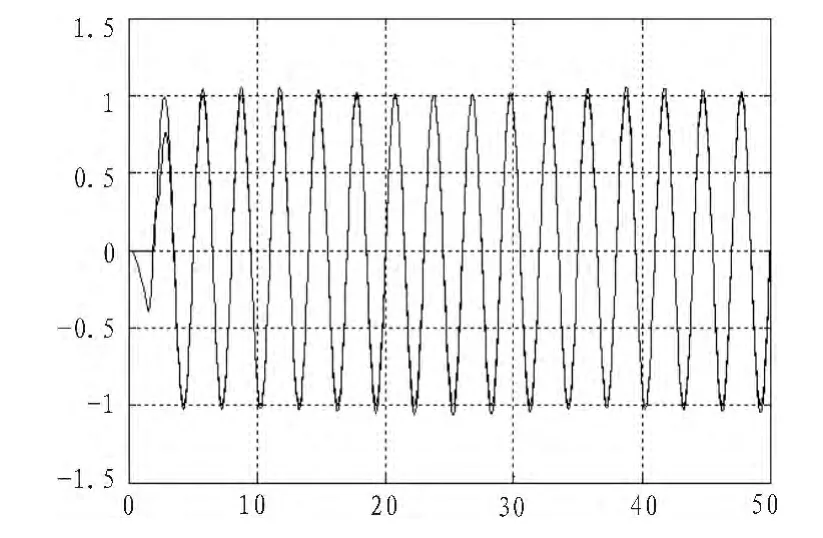
图8 带通滤波后信号时域波形Fig.8 Time-domain waveform of the BP filtered signal

4 结论

MATLAB仿真可以非常方便设计出具有严格线性相位要求的滤波器，在应用中只需对程序中滤波器的起始频率、截止频率、采样频率和窗函数等参数进行修改就可实现需要的滤波功能，实用性强[7]。

采用组合积分系统滤波是在数字滤波算法的基础上提出的一种新的滤波算法，通过构建系统模型，根据需求调节延时常数、、及常数来实现滤波，简单易懂，易操作。下一步工作是采用该方法对其它周期信号（方波、三角波）进行有效的设计，实现滤波效果。

[1] 李鹏，李树广.基于DSP和CPLD的有源滤波器数据采集系统设计[J].测控技术，2012（5）:73-76.LI Peng，LI Shu-guang.Design of data acquisition system used for APF based on DSP and CPLD[J].Measurement&Control Technology，2012，5（31）:73-76.

[2] 王坤.基于DSP的FIR数字滤波器设计研究[J].制造业自动化，2012（15）:147-149.WANG Kun.The FIR digital filter design based on the DSP[J].Manufacturing Automation，2012，34（8）:147-149.

[3] 解伟，张晓斌，张朋松，等.飞机电源控制器PCU测试仪的设计与实现[J].计算机测量与控制，2010（9）:2207-2209.XIE Wei，ZHANG Xiao-bin，ZHANG Peng-song，et al.Design of tester system for power control unit（PCU）[J].Computer Measurement&Control，2010，18（9）:2207-2209.

[4] CHE I-Lung，PENG Sheng-chun，LIU Jun-hong.Simple control method for integrating processes with long deadtime[J].Journal of Process Control，2002：123.

[5] Ibrahim Kaya.Obtaining controller parameters for a new PIPD Smith predictor using autotuning[J].Journal of Process Control，2003：135.

[6] Morari Manfred，Zaririous Evanghelos，Robust process control[J].1989，N.J.:Prentice Hall，Englewood Cliffs.

[7] 郑佳春.数字信号滤波器的MATLAB设计与DSP实现[M].北京：机械工业出版社，2003.

[8] 凌生强，廖柏林，丁亮，等.基于Matlab的FIR带通滤波器设计及DSP实现[J].现代电子技术，2012（9）:176-178，186.LIN Sheng-qiang，LIAO Bai-lin，DING Liang，et al.Design of FIR band-pass filter based on Matlab and its implementation with DSP[J].Modern Electronics Technique，2012（5）:176-178.