线性回归参数的总体最小二乘估计新算法

徐 陶，刘国仕，俞 友，吴泽强

（1．湖南省地质矿产勘查开发局402队，湖南 长沙410014；2．湖南省勘测设计院，湖南 长沙 410014；3．长安大学 地质工程与测绘学院，陕西 西安710054）

关于总体最小二乘原理在测量数据处理中的应用，近年来测量学者们已进行广泛的研究，并针对测量平差模型提出一些解决总体最小二乘问题的算法［1－4］，这些算法对总体最小二乘原理在测量数据处理中的应用有着重要的作用。但对于考虑自变量误差的线性回归问题，这些算法有一定的局限性。这是因为线性回归模型中的系数矩阵存在常数列，对其也进行改正是不合理的。一般对于线性回归的总体最小二乘求解都是采用混合总体最小二乘法［5－7］，但混合总体最小二乘法采用的矩阵分解不利于测量人员理解且没有考虑到测量平差的优势。文献［12］先将数据中心化，即分离线性回归系数矩阵中的常数列，再采用奇异值分解法进行回归参数求解。这样处理比较合理，但计算较为复杂。文献［13］提出一元线性回归的总体最小二乘迭代算法，但没有统一到多元线性回归模型。鉴于此，本文在一元线性回归总体最小二乘平差模型的基础上，推导了解线性回归参数的总体最小二乘迭代算法，并给出算例，证明算法在进行线性回归参数估计时的正确性和合理性。

1 算法推导

1．1 一元线性回归总体最小二乘算法

一元线性回归总体最小二乘平差模型为

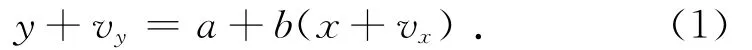
式中：y ＝ ［y1… ym］T，x ＝ ［x1… xm］T，vy＝［vy1… vym］T，vx＝ ［vx1… vxm］T。将式（1平差模型展开后按总体最小二乘原理引入平差约束条件为

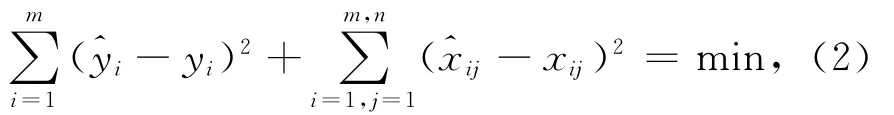
由式（2）再结合式（1），则可构造目标函数为

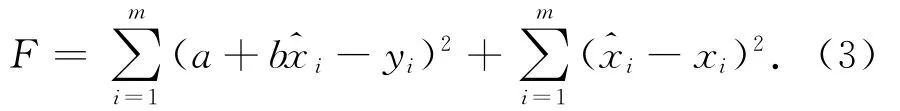
由式（3的目标函数可知其含有m＋2个未知数，其中2个为线性回归参数a，b，其余的m个为改正后的自变量＾xi，要求取满足式（2）的参数值，即将F分别对a，b，＾xi求导，并令其等于0。

其中F对＾xi求导有m个式子，将其整理化简后得

F对a，b求导共有2 m个式子，将其整理化简后得

将式（4）写成矩阵形式为

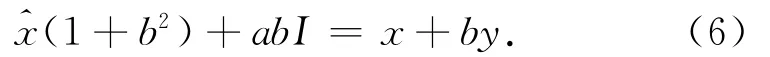
由于式（5）是F对回归参数a，b求导，而没有涉及到式（3）中的第二项，因此可以理解为是按最小二乘法求得，只是自变量是改正后的值，而不是原来的观测值。这时式（5）可以表示为

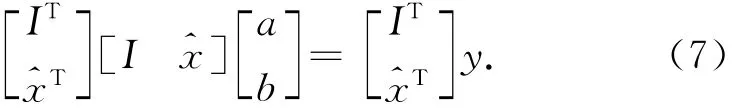
式中I＝ ［1 1 … 1］T，为m×1的向量。式（6）、式（7）即是一元线性回归总体最小二乘迭代算法的基本格式。求解的具体步骤为：①首先按最小二乘原理得到参数的初值a0，b0；②按式（6）计算改正后的自变量＾x；③根据求得的改正后的自变量值由式（7）计算参数值；④重复步骤②和③直到两次计算的回归参数值之差小于给定的迭代限差，则停止迭代输出参数值。

根据迭代计算的回归参数和自变量改正值代入到式（3）中即可求得残差平方和，再根据σ0＝，即可得到单位权中误差。

1．2 线性回归总体最小二乘算法

基于前文的推导，现将一元线性回归扩展到多元线性回归，其总体最小二乘的平差模型为

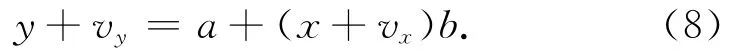
式中：

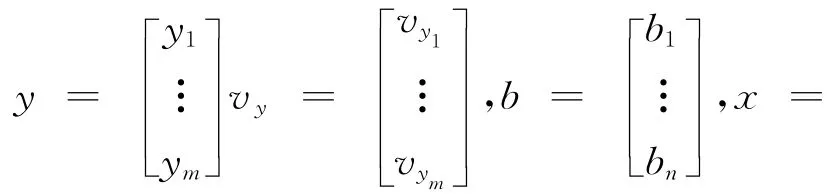
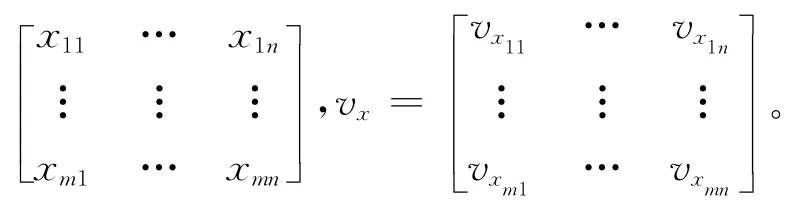
同理将式（8）的平差模型展开后引入总体最小二乘约束条件

由式（9）再结合式（8）即可构造目标函数

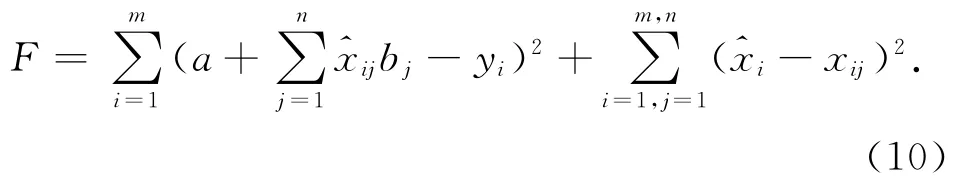
从式（10）目标函数中可以看出，其含有m×n＋n＋1个未知数。其中的n＋1个未知数为回归参数a，bj，其余的m×n个未知数为改正后的自变量。要求得式（8）中满足式（9）的一组回归参数值，即将F分别对a，bj，求导并令其等于0。

其中F对＾xi求导有m×n个式子，见式（11），将其整理化简后得式（12）。

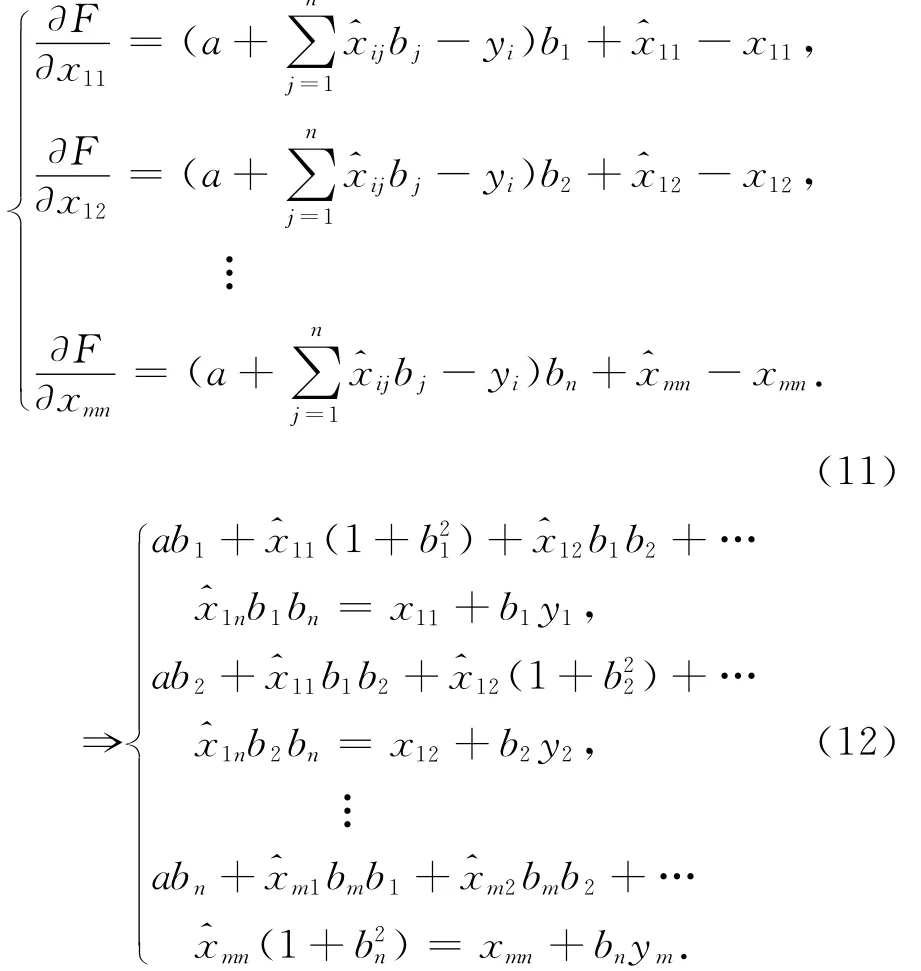
F对a，bj求导共有n＋1个式子，如式（13），将其整理化简后得式（14）。

根据式（11）、式（13）的特点，结合前节所述的一元线性回归总体最小二乘算法推导过程的规律，可以将其写成矩阵形式。式（11可表示为

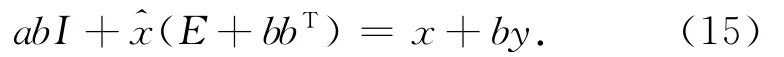
同理式（13）表示为

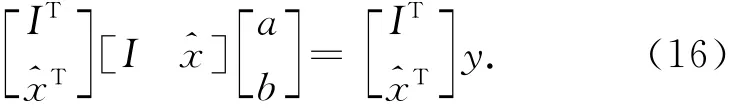
式中I＝ ［1 1 … 1］T，为m×1的向量，E为n阶的单位矩阵。式（15）、式（16）即是多元线性回归总体最小二乘迭代算法的基本格式。当式（8）模型中的n＝1时即变为一元线性回归模型，则式（15）、（16）即可变为式（6）和式（7）。因此式（15）、式（16）便是线性回归总体最小二乘迭代算法的基本格式。

求解的具体步骤为：①按最小二乘原理得到参数的初值a0，b0；②按式（15）计算改正后的自变量＾x；③根据求得的改正后的自变量值由式（16）计算参数值；④重复步骤②和③直到两次计算的回归参数值之差小于给定的迭代限差，则停止迭代输出参数值。

根据迭代计算的回归参数和自变量改正值代入到式（10）中即可求得残差平方和，再根据σ0＝，即可得到单位权中误差。

2 实例分析

为验证本文算法的正确性和可靠性，运用Matlab模拟一个二元线性回归。其方程为：z＝1．5＋x＋2y，在x和y没有误差时求得z的值上加上均值为0，方差为0．03的随机误差，组成观测值。然后分别对x和y添加均值为0，方差为0．03的随机误差，组成新的观测值，如表1所示。分别采用最小二乘法（LS）、总最小二乘迭代算法、文献［13］法、本文算法解算线性回归方程的参数值，并计算其单位权中误差，结果如表2所示。

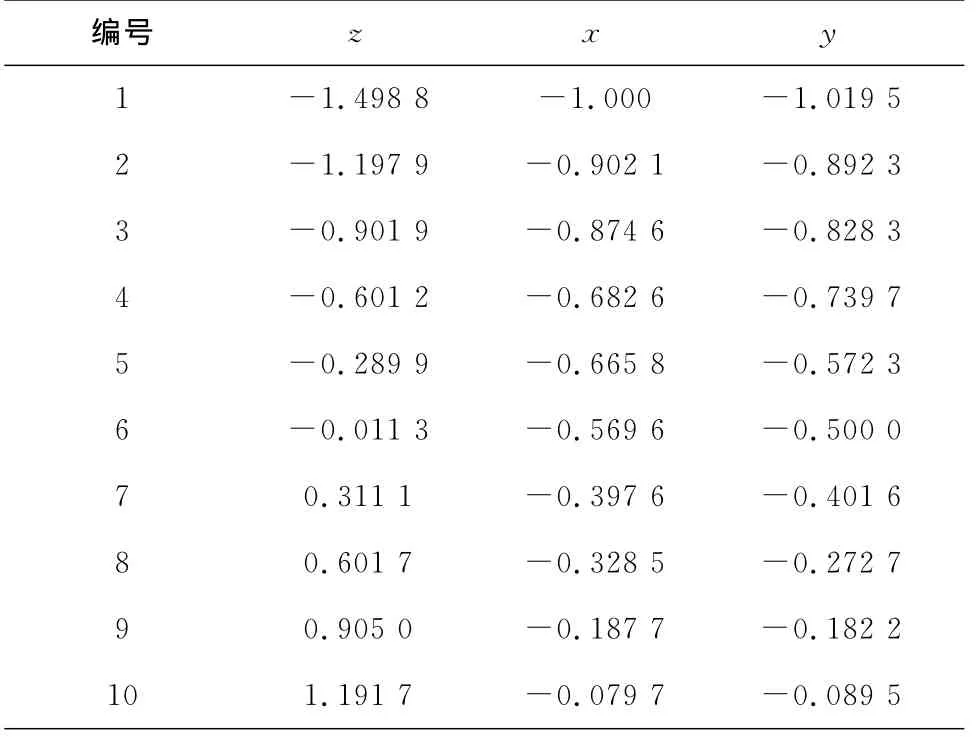
表1 观测数据

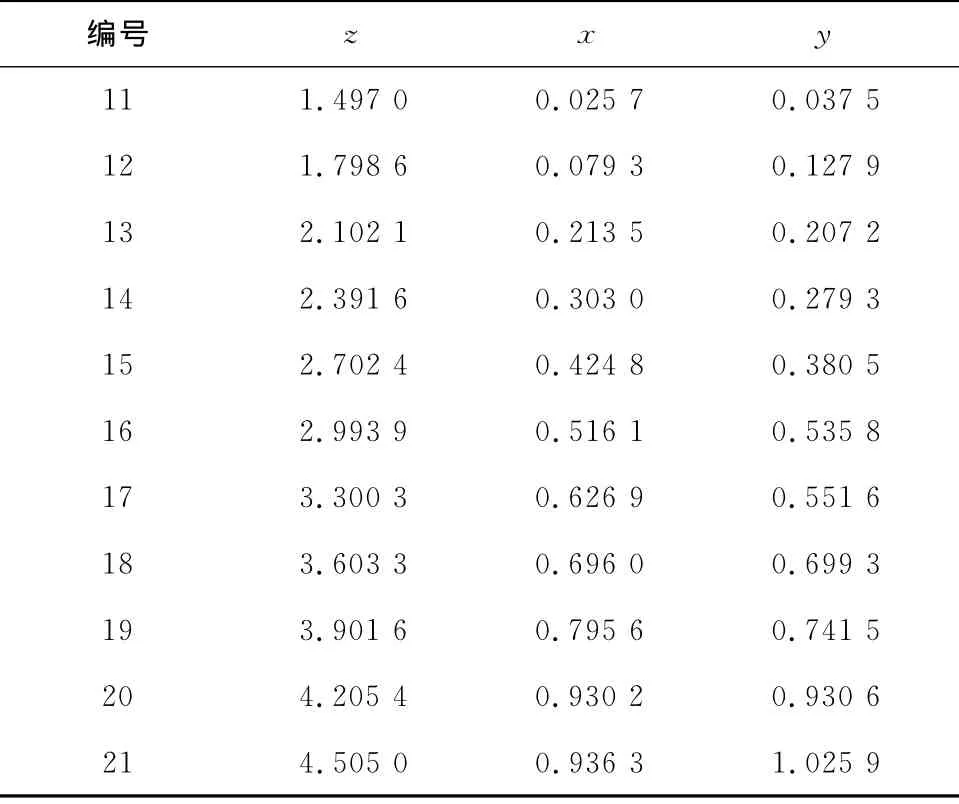
续表1

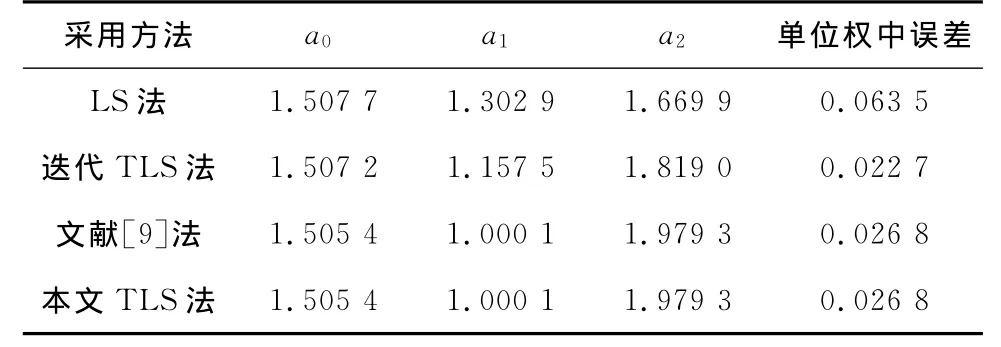
表2 不同方法解算结果比较

从表2可以看出，采用总体最小二乘法比采用最小二乘法求得的回归参数值更可靠，与真值更为接近，而且精度较高。这是因为总体最小二乘法考虑了自变量的误差，提高平差精度。在对比总体最小二乘迭代算法和本文的总体最小二乘算法时可以发现，采用本文算法得到的回归参数值与真值最接近，但单位权中误差却较大。这是由于它们对单位权中误差的评定公式不同。由于常规总体最小二乘法对线性回归模型中的常数列也进行了改正，其改正后的模型为：y＋vy＝（1＋v1）a＋（x＋vx）b，在单位权中误差计算时将常数列的改正值当作一个自变量的改正数，这是不正确的。应该将其乘以回归系数后的值v1a移项到左边，作为因变量的另一部分改正数。如此，计算的单位权中误差为0．028 0，则与实践相吻合。另外，采用本文算法得到的结果与文献［8］法完全一致，故本文给出的算法正确合理。

3 结束语

基于线性回归的总体最小二乘平差模型并以一元线性回归为基础，推导了一种迭代算法。该算法的迭代格式简单，易于编程。相比常规的总体最小二乘算法，既能考虑到线性回归模型中系数矩阵及自变量的误差，又能顾及系数矩阵中的常数列。通过实例分析，结果表明针对线性回归模型的总体最小二乘问题，本文算法可靠合理。

［1］ GOLUB G H，VAN L C F．An Analysis of the Total Least Squares Problem［J］．SIA M J Nu mer．Anal，1980，17：883－893．

［2］ 鲁铁定，周世健．总体最小二乘的迭代解法［J］．武汉大学学报：信息科学版，2010，35（11）：1351－1354．

［3］ 许超钤，姚宜斌，张豹，等．基于整体最小二乘的参数估计新方法及精度评定［J］．测绘通报，2011（10）：1－4．

［4］ 孔建，姚宜斌，吴寒．整体最小二乘的迭代解法［J］．武汉大学学报：信息科学版，2010，35（6）：711－714．

［5］ 邱卫宁，齐公玉，田丰瑞．整体最小二乘求解线性模型的改进算法［J］．武汉大学学报：信息科学版，2010，35（6）：708－710．

［6］ 丁克良，沈云中，欧吉坤．整体最小二乘法直线拟合［J］．辽宁工程技术大学学报：自然科学版 ，2010，29（1）：44－47．

［7］ 孙同贺，罗志才．数字化曲线的整体最小二乘平差［J］．工程勘察，2013（8）：71－73．

［8］ 袁豹，岳东杰，张亮，等．基于总体最小二乘的相似变换模型及其在地图扫描数字化中的应用［J］．测绘工程，2013，22（4）：45－47．

［9］ 李成仁，岳东杰，袁豹，等．基于最小二乘配置的九参数模型在三维坐标转换中的应用［J］．测绘与空间地理信息，2014，37（7）：193－196．

［10］龚循强，刘国祥，李志林，等．总体最小二乘拟合问题求解方法的比较研究［J］．测绘科学，2014，39（9）：29－33．

［11］冯剑桥，黄张裕，徐秀杰，等．总体最小二乘法在坐标转换中的应用［J］．测绘与空间地理信息，2014，37（7）：205－206．

［12］邱卫宁，陶本藻，姚宜斌，等．测量数据处理理论与方法［M］．武汉：武汉大学出版社，2008．

［13］汪奇生，杨德宏，杨建文．基于总体最小二乘的线性回归迭代算法［J］．大地测量与地球动力学，2013，33（6）：112－114．