采用弱基准和抗差估计的重力网平差

赵德军，张敏利，王 强，陈永祥，2

（1．西安测绘总站，陕西 西安710054；2．大地测量与地球动力学国家重点实验室，湖北 武汉430077）

高精度重力测量主要是通过绝对重力测量和相对重力测量来实现的［1］：①绝对重力仪测定的原始观测值中，加入各项改正（包括固体潮改正、海潮负荷改正［2］、气压改正、极移改正、光速有限改正和高度改正）得到基准点的绝对重力值［3］。②相对重力仪测量重力点间的重力段差，再联测至少1个已知重力点即可算出所有未知点的重力值。

鉴于绝对重力仪测量精度有限，重力网平差采用弱基准，所谓“弱基准”是指重力网平差时不固定任何重力点，所有绝对观测量及相对观测量将赋以适当的权，均作为观测量参与平差［4－5］。我国2000国家重力基本网便采用弱基准平差方法［6］。

本文采用弱基准和抗差估计法［7］，按2000国家重力基本网的方法处理了沿海某测区绝对、基本网和一等网重力测量数据［6，8］。

1 平差模型

1．1 相对重力预处理

预处理流程按文献［1］执行：①仪器读数的格值转换；②固体潮改正；③气压改正；④仪器高改正；⑤零漂改正；⑥计算相对联测段差。

本工程测区范围在我国近海，因此预处理时加入了海潮负荷改正。海潮负荷改正执行IERS2003规范，采用重力格林函数与海潮潮高作褶积积分来计算［2］。软件采用美国加州大学开发的“SPOTL”软件包，海潮模型采用德国2011年发布的EOT11 A，该模型是分辨率为7．5′×7．5′的全球海潮模型。

1．2 弱基准平差数学模型

对基准点的绝对重力观测值，可列出绝对重力观测误差方程，其形式为

式中：vi为绝对重力观测残差，gi为i点的平差重力值，g0i为i点绝对重力观测值。

将经过预处理后的每台仪器相邻两点的段差观测值作为观测量，一台仪器在i点和j点之间的段差观测值的误差方程为［1］

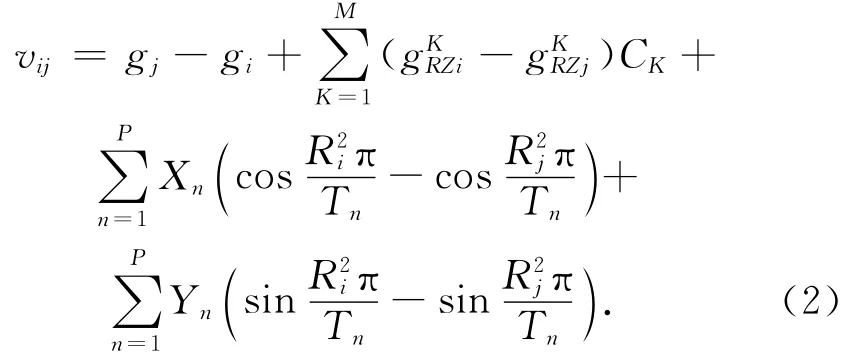
式中：vij为相对观测残差；gi，gj分别为测站i，j点平差后的重力值；gRZi，gRZj分别为测站i，j点经过预处理后的相对联测观测值；Ri，Rj为仪器在测站i，j点的观测读数；CK为重力仪的M 次（一般取1或2）多项式格值函数的K次格值改正因子；Xn，Yn为仪器周期误差参数（对于LCR G型重力仪有7个周期项）［9］。

部分相对观测量含有粗差，因此平差中采用了抗差等价权，对所有的观测量（相对测量、绝对测量）列出如下的误差方程矩阵形式：

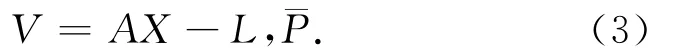
式中：¯P为抗差等价权，未知参数的无偏估计为［4，10］

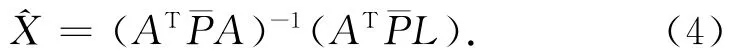
验后单位权中误差

式中，r为多余观测量，未知参数的协方差矩阵

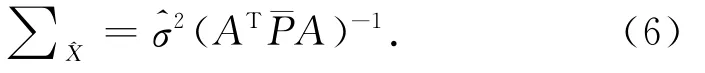
2 重力测量数据处理

某沿海重力测量工程中，用FG5、A10绝对重力仪分别测量了30和4个基准站的绝对重力值，精度在3×10－8～5×10－8ms－2，点位均匀分布在中国近海（见图1）；16台 LCR－G 型、7台 Burris、1台CG－5重力仪联测了80余条基本网测段，400余条一等网相对重力测段。

2．1 预处理精度统计

相对重力段差联测中误差的计算见文献［1］，精度统计如下：

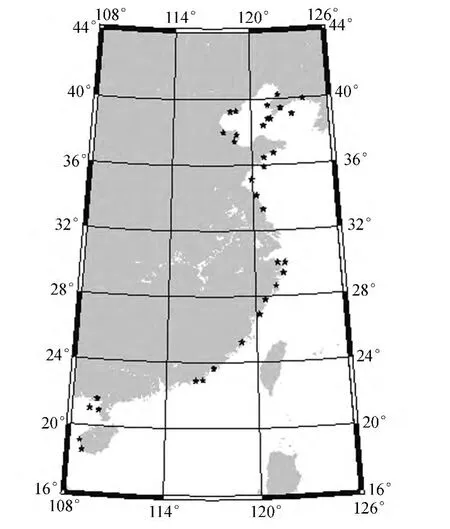
图1 绝对重力点分布图

1）基本网测段联测中误差限差m0为10×10－8ms－2。基本网中13%的测段精度小于1／3m0，30% 介 于 1／3m0～2／3m0，57% 介 于 1／3m0～2／3m0，所有测段精度满足要求。

2）一等网测段中误差限差m0为25×10－8ms－2，部分海上测段可适当放宽到2m0。一等测段29%的精度小于1／3m0，47%介于1／3m0～2／3m0，22%介于1／3m0～2／3m0，2%介于1m0～3／2m0，所有一等测段中误差都满足要求。

3）预处理后的段差按最少边数构成的独立环来计算闭合差，结合文献［1］，闭合差限差

式中：n0，n1分别为构成闭合环的基本网、一等网测段数；m0，m1分别为基本网、一等网段差中误差的限差。相对重力联测路线共形成144个闭合环，闭合差统计见表1。

表1 闭合环闭合差统计

1个闭合环超限，该环是由两个外业队测量的3条测段构成的，外业无法发现闭合环是否超限，因此通过内业抗差降权来处理。表2是构成闭合环的3条测段抗差降权统计，可以看出抗差后验权明显降低，甚至接近于0

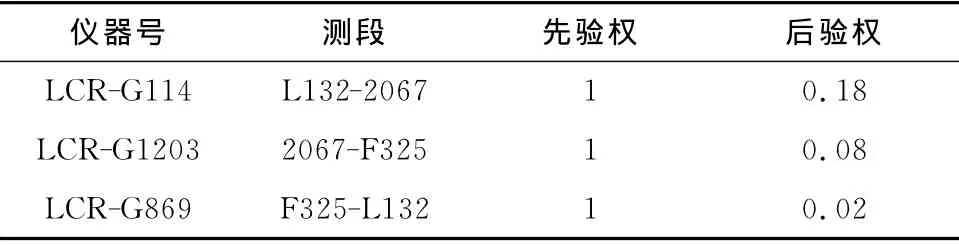
表2 测段抗差降权统计

2．2 观测量权的确定

2．2．1 绝对与相对观测量的权比

绝对与相对观测量的权比为［1］

先验假设，相对重力仪的中误差定为20×10－8ms－2，FG5绝对重力仪优于5×10－8ms－2［3，11］，A10绝对重力仪精度约为9×10－8ms－2，则绝对与相对观测量权比：对于FG5为32∶1，对于A10为10∶1。

2．2．2 相对观测量之间的权比

相对重力仪的测量精度主要受运输工具影响，表3给出了汽车、轮船为载体测量的段差精度统计。

表3 不同载体测量段差统计 10－8 ms－2

则两种载体相对观测量的权比为［6］

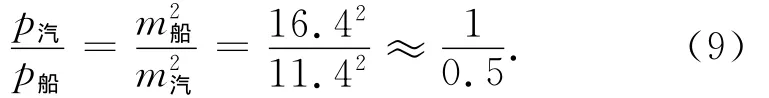
由此确定：绝对重力、汽车、轮船观测值的先验权比为32（10）∶1∶0．5。

2．2．3 抗差估计确权

在参加平差的观测量中，绝对观测量和仪器检定的长基线联测成果均采用先验权且固定权；对于汽车、轮船等观测量先采用先验权，再采用抗差估计定权。

抗差估计采用IGG等价权［4，10］。根据抗差估计理论，经过试算，认为抗差估计等价权模型参数应取为k0＝1．5，k1＝4．5，迭代计算收敛数ε＝2×10－8ms－2，既最大限度采用了原始测量成果，又消弱了含有较大误差的测量成果对平差结果的影响［7］。抗差估计后，共剔除6条粗差，占相对观测方程的0．4%，约110个观测量降权。

2．3 仪器参数的确定

从式（2）中可看出，每台重力仪需要顾及的一、二次格值因子和周期误差参数共16个。若仪器的周期误差参数太多，很可能产生法方程秩亏或不利于提高平差精度，因此必须合理取舍格值因子CK和周期误差Xn，Yn。若仪器参数满足下面的双尾t检验，则可舍去此参数［4，9］。

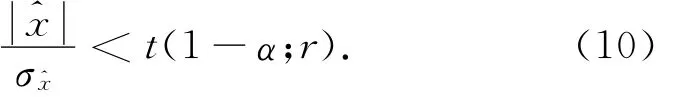
式中：t（1－α；r）表示当置信水平为（1－α），自由度为r（即多余观测量）时，双尾t分布的临界值。反复试算后确定出23台相对重力仪共需顾及89个仪器参数。

2．4 平差结果

1）单位权中误差（单台仪器一测回，汽车联测中误差）为23．6×10－8ms－2。

2）所有重力点平差值的平均中误差为13．6×10－8ms－2；基准点平均中误差为3．8×10－8ms－2；基本点平均中误差为8．9×10－8ms－2；一等点平均中误差为14．3×10－8ms－2；最弱点为永兴岛附近的金银岛为27．9×10－8ms－2。

3）偶然误差特性检验［12］。

残差的正负号个数的检验：正号为873个，负号为887个，正负号残差个数和的绝对值小于置信度为95%的正态分布的限差＝84，n为残差个数，残差符合正态分布。

残差数值和的检验：残差数值和为365×10－8ms－2，小于置信度为95%的正态分布的限差＝1 980×10－8ms－2，残差符合正态分布。

正负残差平方和之差检验：残差平方和之差的绝对值为42 723×10－16m2s－4，小于置信度为95%的正态分布的限差＝80 941×10－16m2s－4，残差符合正态分布。

4）抗差估计剔除粗差后，相对观测量的残差分布如图2所示，从中看出残差分布符合正态分布。

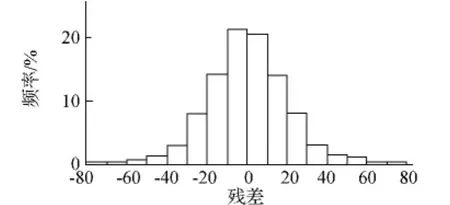
图2 观测残差分布图

3 结束语

绝对重力测量精度优于5×10－8ms－2，但这还不能起到绝对控制重力网的作用，因此采用“弱基准”的方法，将所有绝对重力值和相对重力值当成未知量并赋予适当的权来参与平差。其优点是，若绝对重力值有误差，甚至异常，可从平差结果中发现，且绝对重力值还能通过平差得到改善。

相对重力仪在海上作业观测质量难免较差，甚至出现异常数据，采用抗差估计能有效地降低异常数据的权重，提高平差结果精度。

LCR－G型和Burris重力仪由于其结构特性，要考虑14个仪器周期参数，仪器参数对函数模型有较强的影响，选择有显著影响的仪器参数，能改善计算精度，但是选择合理的仪器参数需要经过大量的试算。因此建议，在重力测量中优先使用无仪器周期误差的重力仪，如CG－5。

［1］ 中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会．GB／T 20256－2006．国家重力控制测量规范［S］．北京：中国标准出版社，2006．

［2］ 王勇，张为民，王虎彪，等．绝对重力观测的潮汐改正［J］．大地测量与地球动力学，2003，23（2）：65－68．

［3］ 张宏伟，董朝阳，赵东明，等．2000国家重力基本网部分站的最新绝对重力测量［J］．大地测量与地球动力学，2011，31（4）：52－55．

［4］ 郝燕玲，姜鑫，周广涛，等．基于小波分析的海洋重力测量滤波算法［J］．测绘科学，2014，39（8）：116－119．

［5］ WANG C，et al．Adjust ment of Relative Gravity Measurements Using Weighted and Datu m－free Constraints［J］．Computers ＆ Geosciences，2002，28：1005－1015．

［6］ 陈俊勇，杨元喜，王敏，等．2000国家大地控制网的构建和它的技术进步［J］．测绘学报，2007，36（1）：1－8．

［7］ 郭春喜，李斐，王斌．应用抗差估计理论分析2000国家重力基本网［J］．武汉大学学报：信息科学版，2005，30（3）：242－245．

［8］ 孙海燕，李斐，晁定波．国家重力基本网的优化设计［J］．武汉测绘科技大学学报，2000，25（6）：496－499．

［9］ 党亚民，丘其宪，徐善．LCR－G型重力仪周期误差的研究［J］．武汉测绘科技大学学报，1996，21（2）：120－123．

［10］杨元喜，宋力杰，徐天河．大地测量相关观测抗差估计理论［J］．测绘学报，2002，31（2）：95－99．

［11］邢乐林，李建成，李辉，等．国内绝对重力观测比对［J］．测绘通报，2008（11）：1－3．

［12］徐良骥．导线网间接平差算法分析与实现［J］．测绘科学，2014，39（3）：107－110．