方腔流动气动噪声边界散射数值预测方法研究
王 芳,刘秋洪,蔡晋生
(西北工业大学航空学院,陕西西安 710072)
方腔流动气动噪声边界散射数值预测方法研究
王 芳,刘秋洪,蔡晋生*
(西北工业大学航空学院,陕西西安 710072)
方腔流动噪声问题因其流场变化复杂且剧烈而倍受关注,本文主要开展高亚声速方腔流动气动噪声数值预测方法研究。基于任意边界条件的格林函数解和Lighthill声模拟理论,提出可以考虑空间边界影响的气动噪声积分计算方法。数值模拟包含流动和噪声计算两部分,通过二阶精度的DDES模型进行流动数值模拟,边界积分方法计算散射声场分布。数值结果显示声场分布随时间呈现周期性变化,与流场的脉动及其脉动周期一致。观察点的声压级随频率逐渐下降且在谐波频率突然增大。本文计算结果与高精度计算气动声学方法计算结果相符,表明该方法合理、可靠,并且具有较高的计算效率。
气动噪声;高亚声速流动;方腔;格林函数
0 引言
随着航空运输量的日益增加,近年来对适航噪声的标准也逐步提高,方腔绕流广泛存在于飞机起落架舱、燃烧室、悬挂物储藏室等构型中,并且方腔流动包含剪切层与方腔内部流动的相互作用、方腔内部流动的自激振荡等多种复杂形式,也是流体与声波相互作用的耦合流动,其流体动力学的不稳定对声场分布产生剧烈影响,方腔噪声的数值预测研究因而成为空气动力学和气动噪声关注的热点。
气动噪声的数值预测方法包括CAA(Computational Aeroacoustics)和 HCAA(Hybrid Computational Aeroacoustics)两类,近年来国内外研究学者在方腔噪声的数值预测方面开展了大量研究工作,Hardin[1]采用DNS(Direct Numerical Simulation)方法研究了二维低速方腔流动噪声,Golerfelt等[2]结合高精度方法探讨了具有层流和湍流边界层的三维方腔流动噪声。国内万振华等[3]也采用DNS方法考察了亚声速方腔流动流致振荡产生的气动噪声。HCAA[4]克服了CAA方法对于网格和数值格式的高要求及限制,且时间效率较高,被广泛的用于复杂流动气动噪声数值预测,并且逐渐发展为一类适用于实际工程问题的方法,有利推动了航空飞行器气动噪声的研究工作。
考虑到HCAA方法在气动噪声研究领域的极大优势,研究学者们提出了诸多性能优良的声学计算模型,主要包括 Curle理论[5]、FW-H(Ffowcs Williams-Hawkings)方程[6]、涡声理论(Vortex Sound Theory)[7]和Kirchhoff方程[8]等。涡声理论阐述了旋涡是声音的本质,然而不能反映声场的多极子特征,并且该方法必须在流场涡量被精确计算的前提下才可以实施。Kirchhoff方程仅能在声波传播的线性区域内执行,对积分边界的选取提出了严格的要求。Curle理论和FW-H方程是Lighthill声模拟理论的拓展形式,其显著优势在于可以考虑固体边界对声场分布的影响,同时从物理角度清晰的解释声波传播的物理本质,因此也成为当前最有效且简单的气动噪声数值计算方法。Golerfelt[9]结合高精度方法和FW-H积分方程研究了二维亚声速开口方腔流动噪声,Ask[10]结合Curle理论考察了低马赫数开口方腔气动噪声声场分布的偶极子特征,Zhang等[11]采用LES模型和FW-H开展了闭合方腔气动噪声的数值预测。然而,上述研究工作存在流场高精度计算的限制,不易开展实际工程应用。作者提出了适用于自由空间内非紧致边界气动噪声的数值预测方法[12],该方法克服了高精度流场计算带来的巨大工作量,不足的是需要计算物理空间的散射声源。
本文基于任意边界条件下点声源的格林函数解和Lighthill声模拟理论,提出可以考虑物理空间边界散射影响的气动噪声数值预测方法,考察了方腔内点应力源的噪声并分析方腔边界的散射影响;同时,深入开展高亚声速方腔流动气动噪声的数值预测,探讨流场与噪声之间的关系。
1 气动噪声数值预测方法
任意边界条件下,单位点声源的传播遵循如下波动方程:
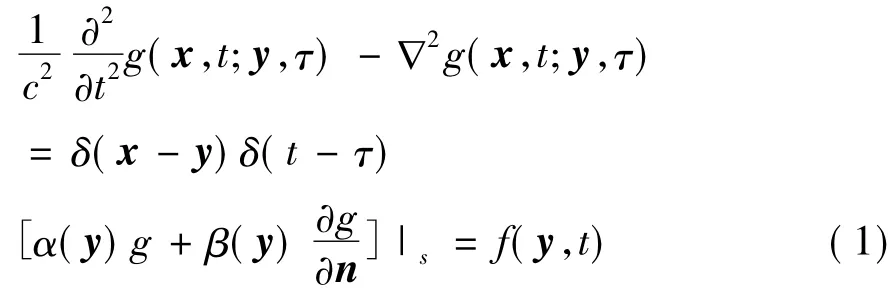
此处g(x,t;y,τ)表示格林函数,又称为声波基本解。c表示声波的传播速度;x、y分别表示观察点和声源点位置。方程(1)描述了τ时刻由y发出的声波经过t-τ时间段到达x的传播过程。图1给出了流场脉动和声波传播示意图,其中y1、y2和y3为声源点,S表示任意结构物体表面,ΓF和ΓA分别表示流场边界和声学远场边界,ΩF和ΩA分别表示流场计算区域和声场计算区域。对于包含空间边界的物理模型,Sb表示其对应的空间边界。
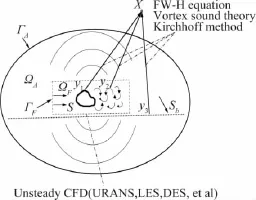
图1 气动噪声传播示意图Fig.1 The diagram of aeroacoustic noise propagation
采用HCAA开展气动噪声的数值计算时广泛使用的Lighthill声模拟理论[13]为

对于高雷诺数流动,可以忽略流体黏性应力带来的影响[14],Lighthill应力张量表示为

式中:p'=p-p0,ρ'=ρ-ρ0分别为压力脉动和密度脉动;p0和ρ0分别表示来流压力和密度;ui为流体沿i方向的运动速度。结合方程(1)、(2)可得

方程(3)可以描述物理空间边界对气动噪声的影响,详细推导过程可参阅文献[12],其中ph和ρh分别表示可压缩流体脉动引起的压力和密度脉动,ρ0表示均匀来流密度。假设规定边界法向方向由物面指向流场区域,vn表示边界沿法向的运动速度,此外Tij=ρuiuj+(ph-c2ρh)δij。对于包含非紧致边界的物理模型成立珔S=S∪Sb。采用方程(3)开展气动噪声的数值计算,首先求解物体表面上的散射声压,然而将观察点布置在物体表面上会出现声源点和观察点距离较近或者相互重合的情形,从而导致数值积分的奇异性。借鉴Khalighi的研究工作,消除积分奇异性可得:

其中z表示物体表面上的观察点,满足‖z-y‖2→0,{z}表示边界珔S去掉z点的剩余部分。对应给出远场噪声计算的表达式:

本文重点考察方腔流动气动噪声,在边界静止的情形下,可以给出方程(4)和(5)的频域形式:

其中G(x,y,ω)为g(x,t;y,τ)的频域形式;ω=2πf,表示圆周频率;f表示频率,假设声场计算的时间步长和采样数目分别为Δt和N,采样定律[14]指出声学计算可分辨的最高截止频率ftop=1/(2NΔt)。以不包含非紧致边界的半空间问题为例,格林函数满足如下边界条件:

此处珔S=Sb,半空间格林函数的表达式可参阅文献[15]。
2 方腔边界散射效应
选取如图2所示的方腔模型,方腔深度2.54mm,方腔长度满足L/D=3,沿流向设置流场计算域,方腔前端长度和后端长度分别为5D和4.8D,方腔前端顶点为坐标原点。假设x、y、z坐标轴分别沿来流方向,腔体深度方向和腔体展向,流场计算区域为x∈[-5D,7.8D],y∈[-D,6.8D],z∈[0,4/3D]。
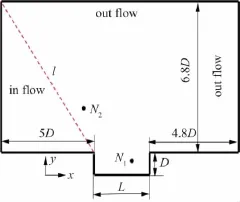
图2 二维方腔流场计算区域Fig.2 The computational field of two-dimensional cavity flow
为了考察方腔边界引起的散射效应,结合半空间格林函数考察单个应力源的噪声,为方便起见取T11=1,T22=T12=T21=0。以方腔展向中间截面为参考面,在方腔内放置两个点源N1和N2,分别位于方腔内部和方腔左端,位置坐标为(2/3L,-1/2D)和(-1/2D,2/3L),给定k0=35,其对应波长λ≈0.18。沿直线l:x+1.4y=0均匀分布100个观察点,图3显示了基于自由空间和半空间格林函数获得的噪声分别用G0和Gb表示,考察不同波数下噪声沿直线的变化规律,其横纵坐标分别对应于和噪声幅值,此处纵坐标采用进行量级处理。图3显示半空间格林函数和自由空间的噪声存在显著差异。与N2相比,由于N1位于方腔内部,边界的散射影响较为强烈,半空间格林函数获得的噪声并不随着波数的增大呈现相同的变化趋势,这与文献[15]获得的结果一致,边界的散射效应使得噪声变化剧烈且复杂。由于N2与方腔边界距离较远,边界的散射影响较小,因而半空间格林函数获得的噪声与自由空间几乎保持相同的变化趋势。唯一不同的是其声压幅值沿直线先增大后减小,这是因为随着r的增大,声源N2与观察点的距离先增大后减小,也符合声波的传播规律。半空间格林函数获得噪声与自由空间格林函数噪声的数值差异说明方腔边界的散射效应不容忽视,并且应力源受到的散射影响与其物理位置密切相关。


图3 不同波数下自由空间和半空间格林函数获得的噪声Fig.3 The noise of free and half space Green's function with different wavenumber
3 方腔流动噪声数值计算
3.1 方腔流动计算
已知自由来流马赫数为0.8,来流温度为T= 298.15 K,声波传播速度为c=346.14 m/s,来流速度为276.91 m/s,来流密度为ρ=1.269 6 kg/m3,相对于方腔深度的雷诺数为48 600。非定常流场数值计算的步长为Δt=10-8s,采用基于SA模型的二阶精度DDES方法[16]进行计算。采用Block网格划分技术将计算区域划分为168块,方腔内部包含48个网格块,且沿流向和深度方向分布的网格密度为257× 193,沿深度方向网格距离壁面最小距离为10-5m。展向均匀分布33层网格,腔内网格数目约164万,腔内与腔外整个流场计算域的三维网格单元总数近280万。方腔底部沿流向分布选取展向分布的中间截面z=2/3D为参考面,图4给出流动计算获得的不同时刻的涡量云图。起始时刻腔体内部出现流动旋涡,随着时间的延续旋涡产生的新脱落涡不断向腔体后端发展,与腔体后端顶点发生碰撞,导致腔体底部及前端产生分离涡,流场结构发生剧烈变化。方腔内部的流线图分布见图5,方腔内部流线封闭,表明方腔内部逆向流动和剪切层流动呈现交替变化,在方腔中间x=2L/3出现大涡,方腔底部前端和后端分别出现零碎小涡。
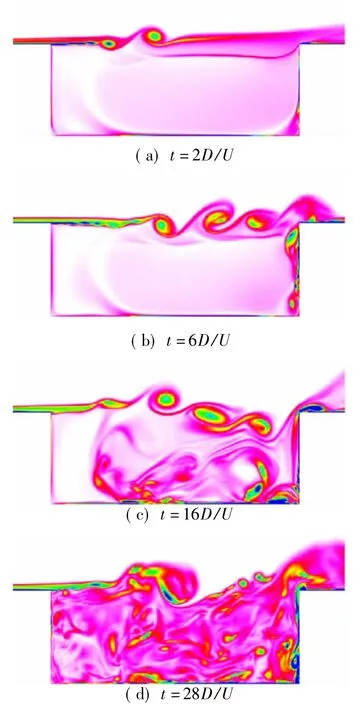
图4 不同时刻方腔内部涡量云图Fig.4 The vortex contours inside the cavity at different time
定义速度均方根值:


图5 方腔内部流线图Fig.5 The streamlines in the cavity
其中u'=u-U0,v'=v-U0,分别表示x、y方向的速度脉动,U0为来流速度。图6给出方腔x=2L/ 3的速度型变化,与Gloerfelt等[2]采用层流模型和Smagorinsky模型获得的结果吻合,其中红色△和蓝色○点分别表示层流和 Smagorinsky模型的结果,蓝色曲线为DDES模拟的结果。与来流速度相比,x和 y方向的速度脉动幅值最高达到30%。流体脉动速度沿竖直方向先增大后减小,并且在y =0附近区域最为剧烈。与方腔内部流动相比,方腔上部流体的脉动速度衰减的更快,这是因为方腔上方形成剪切层,而开式方腔内部受上方剪切层扰动较弱,并且始终存在大涡结构、分离涡及零碎小涡。
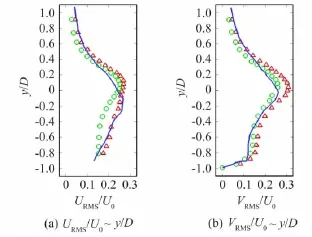
图6 方腔内部x=2L/3速度型分布Fig.6 The distribution of velocity profile inside the cavity with x=2L/3
3.2 方腔噪声计算
考虑到方腔流动的特殊性,假设将方腔底部边界看作半空间边界的一部分,可以按照半空间模型研究方腔噪声。为减少三维模型由于声源样本数目过大所需的巨大存储空间,同时保证声学计算的分辨率,选取展向中间截面z=2/3D的流场为参考面。声学计算每隔5个时间步输出一个样本,对应的时间步长为Δt'=5Δt,首先在x=(-1.04D,4.64D)设置检测点,图7给出了流场压力脉动随时间的变化及该点的SPL随频率(St=fL/U)的变化,表明方腔内部流动呈现不规则的周期性变化,流场脉动周期为T=70Δt',并且声压的能量谱在St数为0.78时达到最大。其次,沿时间方向采集1 050个样本开展声场计算,结合时域方法详细研究方腔流动噪声的瞬时变化并探讨流动与噪声之间的关系,在计算区域布置4 073个网格点,图8给出了声压云图的瞬时分布,以半个周期为间隔输出两个周期的声场计算结果。由图可知,声场分布随时间呈现周期性变化并与流场的脉动及脉动周期一致。由于方腔内部的前端和后端区域流体脉动剧烈,这两个区域的声场脉动也较为强烈;运动旋涡在腔体后端发生分离导致流场发生剧烈变化,声场计算结果表明声波由腔体后端不断向腔体斜上方传播,并且声压幅值随着流场脉动发生周期性变化;流动状态达到稳定之后流场进入下一个脉动周期,声场也呈现相同的周期性变化。图7显示流场的周期大概为 T=70Δt',图8的声压云图显示声场变化周期与流场相同,充分证明流场和声场的一致性,流场脉动较为剧烈的区域噪声也相对强烈,这说明声学计算结果取决于流动计算,同时也验证了当前计算方法的有效性。为了详细研究流场内部局部位置声压的变化及分布,选取如图9所示的曲线,考察不同空间位置的声压分布。红色和绿色实线分别表示直线l1和l2,它们的x、y坐标满足x+1.4y=0和0.85x+y=2.6D,且分别以O和O'为起点,P为终点。在直线l1和l2上均匀布置200个观察点,图10给出了声压幅值分布曲线,此处c1、c2分别对应于直线线l1和l2,其中横坐标分别对应于,表示观察点x与O和O'的距离,例如St=0.78的红色实线表示频率为0.78时声压沿直线的变化。观察图10可知,声压幅值随着频率的增大显著降低,然而相同频率下声场随观察点位置不同而变化,图10(a)显示声压幅值沿直线l1逐渐降低,这与Gloerfelt采用DNS方法[9]获得的结论一致,图10(b)给出的声压幅值在r=3.95D迅速下降,此后声压幅值沿直线l2表现出与直线l1相同的变化趋势。对位于方腔正上方的观察点满足r<3.95D,其噪声幅值变化复杂,涡和二次涡的复杂流场特征密切相关。由此可见,这与方腔内部流动声源脉动剧烈且不断产生分离小图8和图10清晰的揭示了高亚声速方腔流动气动噪声的声场特征及其原因。

图7 流体压力脉动Fig.7 Pressure fluctuation induced by the flow
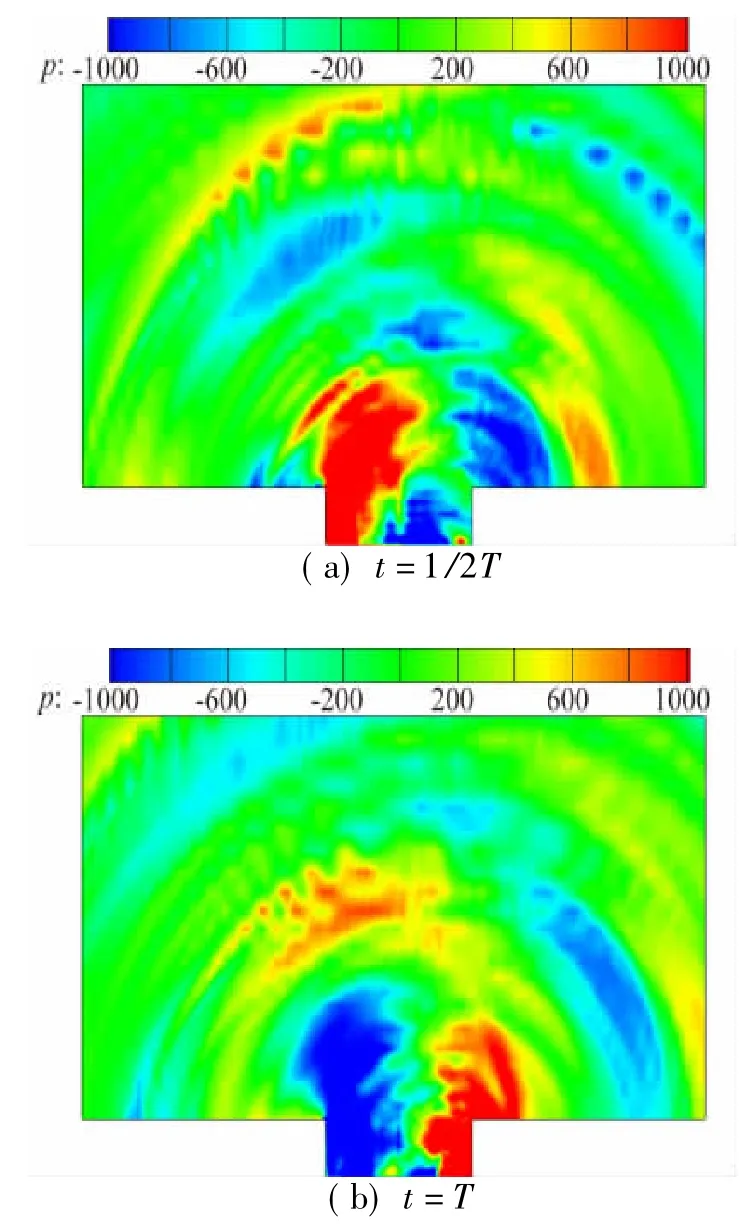

图8 方腔声压云图变化Fig.8 The variations of pressure contours in cavity

图9 声场观察点分布Fig.9 The distributions of observers in acoustic field

图10 声压幅值随观察点的变化Fig.10 The variations of pressure amplitude with different observers
已知图7给出观察点x=(-1.04D,4.64D)的压力脉动及其PSD随频率的变化,声学计算仍然选取上述检测点为观察点,图11给出了声压级随St数发生的变化,并与Gloerfelt采用高精度方法[2]获得的结果进行了数值比较,其中蓝色点线表示Gloerfelt的结果,粉色实线表示当前计算结果。图11显示本文方法获得的声压级在St=0.78达到峰值,与图6(b)给出的流场压力脉动PSD曲线的结论一致,已知Gloerfelt采用高精度方法在St=0.75达到相同的峰值,两者的数值误差仅为4%,并且均与Rossiter公式[17]的预测结果符合。随着频率的增大声压级总体上呈下降趋势,且声压级仅在谐波频率处出现峰值,本文的数值结果与Gloerfelt[2]及Karamcheti[18]获得的结论一致。在高频率下本文方法与Gloerfelt方法的结果显现出数值差异,Lighthill[19]指出低频噪声的能量占总声能的50%以上,可见频率St≤3的噪声携带了大部分声能,并且本文结果是基于二维声场计算修正得到的[20],并不是真实三维流场获得的远场噪声,因而这种数值差异是可以接受的。

图11 观察点声压级随频率的变化Fig.11 The variations of SPL with frequency for observer
4 结论
本文提出了一种可以考虑物理空间边界影响的气动噪声积分计算模型,主要研究高亚声速方腔流动气动噪声并探讨流动与噪声之间的关系,主要结论如下:
(1)采用半空间格林函数可以考虑半空间边界对声场的散射影响且无需计算散射声源,大大节省了计算资源,噪声计算简单且高效。
(2)观察点的声压级在谐波频率处出现明显的峰值,当前方法获得的结果与高精度计算方法吻合,说明这种方法可以精确求解方腔流动边界对气动噪声的散射效应,同时可以避免流场高精度计算所需要的巨大工作量。
(3)声场分布表现出与流场相同的脉动周期和变化特征,流场脉动剧烈的区域其噪声也相对强烈,观察点的流场脉动和噪声脉动表现出相同的变化趋势,反映了流场决定声场的物理事实。
[1]Hardin J C.Sound generation by flow over a two-dimensional cavity[J].AIAA Journal,1995,33(3):407-512.
[2]Gloerfelt X,Bogey C,Bailly C,et al.Aerodynamic noise induced by laminar and turbulent boundary layers over rectangular cavities[C]//8th AIAA/CEAS AeroacousticsConference,Colorado: 2002,2002-2476.
[3]Wan Zhenhua,Zhou Lin,Sun Dejun.Numerical investigation of flow-induced oscillations and noise from a rectangular cavity[J].Acta Aerodynamica Sinica,2012,30(3):291-298.(in Chinese)万振华,周林,孙德军.方腔流致振荡及噪声的数值研究[J].空气动力学学报,2012,30(3):291-298.
[4]Bailly C,Bogey C,Gloerfelt X.Some useful hybrid approaches for predicting aerodynamic noise[J].Competes Rendus Mechnique,2005,333:666-675.
[5]Curlen N.The influence of solid boundaries on aerodynamic sound[J].Proceedings of the Royal Society of London,Series A,1952,213(1187):505-514.
[6]Ffowcs Williams J E,Hawkings D L.Sound generation by turbulence and surface in arbitrary motion[J].Proceedings of the Royal Society of London,Series A,Mathematics and Physical Sciences,1969,264:321-342.
[7]Howe M S.Theory of vortex sound[M].New York:Cambridge U-niversity Press,2003.
[8]Farassat F,Mayers,M K.Extension of Kirchhoff's formula to radiation from moving surfaces[J].Journal of sound and vibration,1988,123:451-461.
[9]Gloerfelt X,Bailly C,Juve D.Direct computation of the noise radiated by a subsonic cavity and application of integral methods[J].Journal of Sound and Vibration,2003,266:119-146.
[10]Ask J,Davidson L.Sound generation and radiation of an open twodimensional cavity[J].AIAA Journal,47(6):1337-1349.
[11]Zhang N,Shen H C,Yao H Z.Numerical simulation of cavity flow induced noise by LES and FW-H acoustic analogy[J].Shanghai: 9th International Conference on Hydrodynamics,2010,242-247.
[12]Wang Fang,Liu Qiuhong,Cai Jinsheng.An unified aeroacoustic computational integral method of noise radiation and scattering with noncompact bodies[J].Acta Aeronautica et Astronautica Sinica,2013,34(11):2482-2491.(in Chinese)王芳,刘秋洪,蔡晋生.非紧致结构气动噪声辐射/散射统一积分计算方法[J].航空学报,2013,34(11):2482-2491.
[13]Lighthill M J.On sound generated aerodynamically.I.General theory[J].Proceedings of the Royal Society of London,Series A: Mathematical and Physical Sciences,1952,211(1107):564-587.
[14]Morfey C L.The role of viscosity in aerodynamic sound generation[J].Acoustics,2003,2(3):225-240.
[15]Wang F,Cai J S,Liu Q H.Aerodynamic noise calculations of ground effect based on tailored Green's function[J].Journal of Aircraft,2015,52(1):21-30.
[16]Cai J S,Pan S C,Li W F,Zhang Z K.Numerical and experimental investigations of a nonslender delta wing with leading-edge vortex flap[J].Computers and Fluids,2014,99:1-17.
[17]Rossiter J E.Wind-tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds[R].London:Her Majesty's Stationery Office,1964.
[18]Karamcheti M.Acoustic radiation from two-dimensional rectangular cutouts in aerodynamic surfaces[R].Washington:National Aeronautics and Space Administration,1955.
[19]Lighthill M J.On sound generated aerodynamically.II.Turbulence as a source of sound[J].Proceedings of the Royal Society of London,Series A:Mathematical and Physical Sciences,1954,222 (1148):1-32.
[20]Orselli R M,Meneghini J R,Saltara F.Two and three-dimensional simulation of sound generated by flow around a circular cylinder[C]//15th AIAA/CEAS Aeroacoustics Conference,Flordia:2009,2009-3270.
Numerical prediction method of aerodynamic noise including boundary scattering generated by high subsonic cavity flow
Wang Fang,Liu Qiuhong,Cai Jinsheng*
(1.School of Aeronautics,Northwestern Polytechnical University,Xi'an 710072,China)
The aerodynamic noise of cavity flow is a concern problem due to the complex and serious dynamic fluctuation,the goal of this paper is to study the numerical prediction method of aerodynamic noise generated by high subsonic cavity flow.With the help of Green's function satisfied arbitrary boundary conditions and Lighthill's Acoustic Analogy,the aeroacoustic integral computational method taking into account the influence of physical boundary is presented.The numerical calculation includes two parts,flow and noise computations.The two-order DDES model is used to perform the fluid simulation while the present integral computational method calculates the distribution of scattering noise.Numerical results show that the distribution of noise field varies periodically,and it is in agreement with fluid fluctuation.The SPL gradually reduces with frequency and appears higher amplitudes at harmonic frequencies.Numerical results obtained with the present method agree well with that of high-order aeroacoustic computational method,which indicate that this method is valid and efficient to calculate high subsonic cavity noise.
aeroacoustic noise;high subsonic flow;cavity;Green's function
V211.3
:Adoi:10.7638/kqdlxxb-2015.0004
0258-1825(2015)05-0617-07
2015-01-06;
:2015-03-03
国家自然科学基金(11002116);西北工业大学基础研究基金(GCKY1006)
王芳(1984-),女,宁夏人,博士研究生,研究方向:气动噪声算法研究及数值预测.E-mail:fangw1211@163.com
蔡晋生*,西北工业大学航空学院.Tel:13659115379,E-mail:caijsh@nwpu.edu.cn
王芳,刘秋洪,蔡晋生.方腔流动气动噪声边界散射数值预测方法研究[J].空气动力学学报,2015,33(5):617-623.
10.7638/kqdlxxb-2015.0004 Wang F,Liu Q H,Cai J S.Numerical prediction method of aerodynamic noise including boundary scattering generated by high subsonic cavity flow[J].Acta Aerodynamica Sinica,2015,33(4):617-623.

