干扰剪切流动稳定性理论及其对高雷诺数流动数值模拟方法的改进

高 智

（中国科学院力学研究所高温气体动力学国家重点实验室，北京 100190）

干扰剪切流动稳定性理论及其对高雷诺数流动数值模拟方法的改进

高 智＊

（中国科学院力学研究所高温气体动力学国家重点实验室，北京 100190）

在干扰剪切流（Interacting Shear Flow，ISF）理论的基础上，提出ISF稳定性理论并把它用于改进高雷诺（Re）数流动计算方法。（1）高Re数内外绕流的RANS计算及工业标准PNS计算中，流动转捩的预测均基于经典边界层理论；然而转捩并非总是最早发生在边界层中，例如发生在壁面小突起、小凹坑、小窄缝等局部粘性/无粘强干扰区，这些强干扰区可能位于边界层内，但边界层理论并不适用于它们，又如转捩发生在分离点邻域强干扰区等。（2）ISF理论表明：高Re数内外绕流为一复杂ISF，转捩总是最早发生在该ISF的层流区中。（3）ISF稳定性理论表明：作者提出的干扰剪切扰动流（Interacting Shear Perturbed Flow，ISPF）方程组可以计算ISF层流中非湍流扰动运动演化并预测转捩；ISF方程组和ISPF方程组分别与PNS和抛物化稳定性方程（PSE）为同类方程组，PSE分析计算边界层稳定性的众多成功实践，说明用ISPF（即PSE）方程组计算ISF层流扰动流并预测转捩完全可行。（4）RANS和PNS方法经ISF稳定性理论改进后，在转捩前用ISF方程组（即PNS）计算ISF层流基本流，用ISPF方程组（即PSE）计算ISF层流扰动流并预测转捩位置；转捩后RANS方法计算RANS或RANS/LES，PNS方法计算干扰剪切湍流（ISTF）方程组即抛物化RANS（PRANS）方程组。改进后的两方法，理论合理正确，方程体系完备、自洽，ISF方程组只能用ISPF方程组相配对，因此是高Re数内外绕流计算的理想且可持续发展的两种方法。

高雷诺数流动；PNS方法；RANS方程；干扰剪切流（ISF）理论；ISF稳定性理论

0 引 言

高雷诺（Re）数流动的数值模拟是科学问题，也是众多工程技术领域的重大需求，多年来涌现了计算高Re数流动的大量文献。通常认为Navier-Stokes（NS）方程可以描述高Re数湍流流动，并且认为在最小空间尺度（Kolmogoroff尺度）网格下的NS方程高精度高分辨率计算，即直接数值模拟（DNS），可以获得最小尺度层次上的湍流统计平均特性或流动。但对具有工程价值的实际流动，DNS的难度和耗费都很大，文献［1］估计具有工程使用价值的湍流DNS到2080年才能实现。未来五、六十年时期内，湍流计算主要是RANS方程计算［1］和工业标准气动计算的PNS方程计算［2］，这两种计算都必须补充湍流模型和转捩模型，这些模型都具有经验性且都缺乏普适性。湍流模型已有广泛、丰富的研究和众多的应用计算，转捩模型的知识相比较欠缺，借助经验估算转捩位置的计算方法均基于粘性边界层稳定性理论［3-4］，主要的如：转捩模型方法，即建立边界层间歇因子模式方程并植入湍流模型计算中（如见［5-6］）；经验转捩准则方法，即根据风洞和飞行实验资料归纳出边界层相关特征量在转捩处满足的经验转捩关系（准则），例如边界层动量厚度和外缘马赫数满足的经验转捩关系（准则）［7-8］等；应用较广泛的是半经验eN方法［9-13］，该方法利用边界层线性稳定性理论（LST）或抛物化稳定性方程（PSE）计算扰动幅值增长率，沿扰动传播方向积分增长率获得扰动的相对增长倍数eN，当边界层中最不稳定波的增长倍数达到某一经验值（或NT≈9.0～11）时，边界层发生转捩。

然而必须指出针对本文研究的高Re数内外绕流问题，许多重要的流动转捩并非总是最早发生在经典边界层中，例如转捩发生在壁面小突起、小凹坑、小台阶和小窄缝等所谓三层（Triple-deck）理论点邻域的局部粘性/无粘强干扰流动中［3］，这些三层局部干扰区可能位于经典边界层内，但边界层理论及其稳定性理论并不适用于它们，又如转捩发生在分离点、尾缘点邻域的强干扰流动中，管道和喷管顺轴流的来流中心扰动严重时转捩发生在管道中心区的情况，都不是在经典边界层中发生转捩；特别是波系干扰严重的超声速绕流和激波十分贴近壁面的高超声速绕流，经典边界层现象可能不明显甚至不存在。另一方面，粘性/无粘干扰剪切流动（ISF）理论［14-16］表明：高Re数内外绕流是一复杂ISF，经典边界层仅是ISF粘性层中的一小段。例如高超声速钝头锥绕流，激波和壁面之间的整个激波层为一复杂粘性/无粘干扰剪切流（ISF），参见图1，绕流转捩前为ISF，包括干扰剪切层流基本流（ISLBF）和干扰剪切扰动流（ISPF），转捩后为干扰剪切湍流（ISTF）。因此利用边界层理论预测转捩，首先要在ISF基本流中找出边界层，并计算边界层方程及其稳定性方程，然后把它们与ISF基本流计算相耦合；局部边界层计算与ISF基本流计算显然不相匹配，理论逻辑上也不合理。应当指出：对ISF层流基本流计算，与它相匹配的扰动流计算就是干扰剪切扰动流（ISPF）方程组计算，因此联立求解ISF方程组和ISPF方程组计算ISF层流基本流及扰动流，即ISF稳定性理论计算必将导致高Re数流动数值模拟方法的实质性改进。本文简述了ISF理论及与PNS的关系，干扰剪切扰动流（ISPF）理论、方程组及与抛物化稳定性方程（PSE）［9-13］的关系，ISF第一和第二稳定性理论，ISF稳定性理论及其推论并用于改进高Re数绕流流动的数值模拟方法。

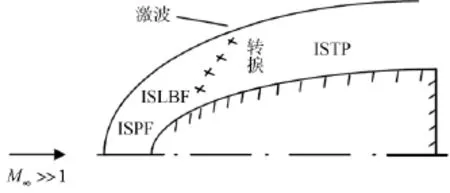
图1 高超声速钝头锥绕流，激波和壁面之间的整个激波层为复杂干扰剪切流（ISF），转捩前为干扰剪切层流基本流（ISLBF）和干扰剪切扰动流（ISPF），转捩后为干扰剪切湍流（ISTF）Fig.1 Shock-wave layer in a hypersonic flow over blunt-cone-body is a complex interacting shearflow（ISF），that is interacting shear laminar basic flow and its perturbed flow before transition andinteracting shear turbulent flow（ISTF）after transition

1 干扰剪切流动（ISF）理论、ISF方程组及与PNS的关系

作者提炼出的干扰剪切流动（ISF）由粘性剪切层及与它相互作用的相邻无粘外流组成，ISF的核心流动规律是粘性层流向对流占优、法向对流扩散相竞争，该规律的数学定义式对二维流是：

这里f＝（u，v），u、v为粘性层流向（x方向）和法向（y方向）流速分量，ρ和μ分别为密度和粘性系数。作者［17］导出ISF粘性层的长度和速度尺度律为：

其中（xp，yp，zp）＝（x，y，z）/L，（up，vp，wp）＝（u，v，w）/U，ReL＝ρUL/μ，，0≤q≤ 1/2，q为干扰参数。q＝0，ISF表示驻点流也表示经典边界层和相邻无粘外流（两者之间无干扰）；q＝1/4，ISF的粘性层正是三层干扰流的下层［3］，此时的ISF表示三层干扰流动。可见高Re数内外绕流近壁粘性/无粘层流是若干局部区域ISF组成的复杂ISF；描述该复杂ISF显然必须使用贴体正交曲线坐标系，否则ISF数学定义式（1）和（2）不成立。

ISF方程组与PNS的关系：利用ISF数学定义式化简NS得到ISF方程组，ISF方程组与熟知的抛物化NS（PNS）为同类方程组。因此，对内外绕流近壁粘性/无粘层流，ISF（即PNS）方程组是完全NS方程组的合理近似，这就从理论上解释了ISF（PNS）方程组为什么具有普适价值，PNS方法为什么得到广泛应用并成为工业标准气动计算的基础［2］。PNS是20世纪六七十年代人们为计算大范围ISF（例如尖和钝前缘平板高超声速绕流，横向压力梯度不可忽略的射流和混合层流动，钝头体高空超声速绕流，两板垂直相交的顺角流及矩形截面管道和圆管内外顺轴流，小钝头细长锥和尖头细长锥高超声速绕流等）而提出的，PNS有些略有差异的不同形式，称呼也不相同，但它们有相同的数学性质，即抛物化性质，对它们的求解初边值数学提法适定，不需要规定流向下游边界条件，且沿流向可对它们实施空间推进求解，使计算维数减少一维，在流向马赫数大于1时，又可对它们实施高效的单次空间推进求解［19-21］。在这些大范围ISF中往往会出现湍流，此时必须用干扰剪切湍流（ISTF）方程组［15-16］，即抛物化RANS（PRANS）方程组替代NS方程组。不难看出提出PNS所考虑的这些大范围粘性/无粘流动其实也是若干局部区域ISF组成的复杂ISF。

应当指出，人们早先并没有弄清楚PNS到底描述什么基本流动，适不适用于驻点流等问题。ISF理论解决了上述问题，它就是PNS的流体力学基本理论，因此ISF理论亦被称作PNS理论［21］。对不可压缩二维驻点流和三维非定常驻点流，文献［22］已证实ISF（即PNS）方程组解与完全NS方程组解完全一致；对分离区小的内外绕流，众多计算证实［19-21］ISF（即PNS）方程组数值解与完全NS方程组数值解很好相符。因此对高Re数内外绕流有粘/无粘层流（即ISF），ISF（即PNS）方程组是完全NS方程组的合理且很好的近似方程，正像文献［23-25］论述的薄层（TL）NS（即PNS）方程组丢掉的粘性小项在寻常的NS计算中是算不出来的，理应丢掉这些粘性小项，且丢掉它们带来的误差小于湍流模型引起的误差，这是ISF（即PNS）方法成为工业标准气动计算基础的另一原因。最后有必要指出，ISF（即PNS）理论［14-17］不仅使早期说法不一的PNS诸方法能够自圆其说，把PNS诸方法统一在一个理论之中；而且ISF理论在高Re数流动的PNS方程以及NS方程和RANS方程数值计算中都有一些重要的应用，例如在计算网格设计和壁面边界条件选择中的应用，在PNS方程和NS方程计算结果可信度评估方面的应用［21］，特别是ISF粘性层长度尺度律［17］揭示了ISF中粘性/无粘干扰将导致粘性层产生小尺度干扰流动（例如三层干扰流动），这些小尺度干扰流动将导致物理量（例如壁面热流）局部突增，而对高超声速绕流，局部强干扰引起的热流突增等气动现象将导致飞行器局部受损，甚至造成飞行事故［26］，因此在PNS方程以及NS方程计算中，很有必要根据ISF粘性层长度尺度演化规律，分辨并计算好这些小尺度干扰流动结构。

2 干扰剪切扰动流（ISPF）理论、ISPF方程组及与PSE的关系

在讨论ISF稳定性问题之前，先简述作者提出的干扰剪切扰动流（ISPF）理论及ISPF方程组［15-16］，并考察ISPF方程组与抛物化稳定性方程（PSE）［27-28］的关系。层流运动的稳定性通常根据层流中小扰动（即非湍流扰动）的演化来确定［3］，ISF的稳定性因此由干扰剪切扰动流（ISPF）方程组的解来确定。ISPF是存在非湍流扰动运动的ISF，按照作者［15-16］的考虑，ISPF由粘性剪切扰动流及与它相互作用的相邻无粘扰动外流所组成，粘性剪切扰动层在流向对流占优，法向对流扩散竞争，数学定义式为［15-16］：

其中f′＝u′、v′、w′和T′，分别为流速分量u、v、w和温度T的非湍流扰动量，并有，，y方向为ISPF粘性剪切扰动薄层的法向。按照流动稳定性理论［3］的通常处理，认为和u＝（u，v，w）均满足NS方程，为未扰ISF流速矢量，由u的NS方程组减去珔u的NS方程组得到支配非湍流扰动运动的控制方程组，再利用式（4）进行简化，得到干扰剪切扰动流（ISPF）方程组，对不可压缩流和直角坐标系中的情况有：

对远场采用自由来流条件。线性ISPF（LISPF）方程组和非线性ISPF（NISPF）方程组可用来确定近壁ISF中非湍流扰动运动的演化，结合实验资料又可预测转捩。应该提到ISPF方程组与ISF方程组都应在贴体坐标系中写出，不过从完全NS扰动方程组到ISPF方程组的抛物化简化处理，贴体正交曲线坐标系和直角坐标系下抛物化简化处理完全类似。

ISPF方程组与抛物化稳定性方程（PSE）的关系，PSE是Herbert和Bertolotti在1987提出的［27］，他们从原始变量NS扰动运动方程组出发，采用模（mode）-振幅函数分析方法，在扰动是时间周期函数的假设下，把原始扰动变量φ′＝（u′，v′，w′；T′，ρ′）转换到复数形式振幅函数。对线性PSE（LPSE）：

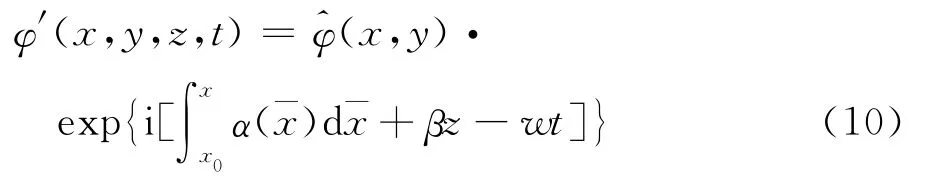
其中α、β是复数形式的流向和展向波数，w为频率。对非线性PSE（NPSE）仍然假定原始扰动变量是时间和展向Z的周期函数，由于非线性作用将激发高次谐波，且假定高次谐波的波数和频率是基本波数和频率的整数倍，原始扰动变量展开为Fourier级数：

通过考虑不难发现，把线性和非线性ISPF方程组中原始变量转换为振幅函数变量，于是得到线性和非线性PSE；反之，把线性和非线性PSE中的振幅函数变量逆转为原始扰动变量，于是得到线性和非线性ISPF方程组。因此PSE与ISPF方程组一样，它们都适用ISF、适用于高Re数内外绕流近壁有粘/无粘层流流动。不幸的是，从一开始PSE就被局限于ISF的粘性/无粘无干扰或弱干扰流动区域即边界层区域［27］，丢掉了PSE还适用的ISF中粘性/无粘强干扰的流动区域，特别是丢掉了PSE对ISF整个流动区域的适用性。PSE提出近三十年来，众多学者利用它分析了边界层的稳定性特性，获得了有价值的丰硕成果［4，9-13，28］。主要的成果如线性PSE算出中性稳定曲线比边界层线性稳定性理论（LST）的结果更接近实验，且既能考虑流动的非平行性，计算量又比LST小；用非线性PSE算出的结果（包括基本流动，高次谐波以及对基本流修正的幅值与剖面等）与直接数值模拟（DNS）的结果很好相符；用非线性PSE算出的高速平面混合层的二维及三维大尺度涡结构亦与DNS的结果很好相符。总之，根据已有的研究成果可得到如下的结论：对ISF粘性层之边界层流动中的非湍流扰动运动演化及转捩发生，PSE和ISPF方程组解是DNS的合理近似；而对ISF粘性层之粘性/无粘强干扰流动区域中的非湍流扰动运动演化及转捩发生、特别是对ISF整个流动区域中的非湍流扰动运动演化及转捩发生，PSE和ISPF方程组解还有待发展和深化。此外应指出：文献［18］证实ISF粘性层和它的扰动流（即ISPF）粘性扰动层存在同一的长度尺度结构，因此若ISF基本流因粘性/无粘干扰而出现小尺度结构和相应的物理量（如壁面热流）突增，则它的扰动流（即ISPF）中也将出现小尺度扰动结构和相应的扰动量突增，扰动量突增无疑与流动转捩密切相关，因此在PSE和ISPF方程计算中，特别在用振幅方程计算时，必须分辨并算好粘性/无粘干扰引起的小尺度扰动结构及相应的扰动量突增。

3 ISF第一和第二稳定性理论

在ISPF方程组研究［15-16］的基础上，本文提出ISF稳定性理论。

ISF第一稳定性理论：对给定的ISF和ISF方程组解，若非湍流扰动（u′，p′），即ISPF方程组（5-6）或式（7-8）的解随时间衰减或放大，则称未扰或称ISF层流基本流分别为稳定和不稳定。

ISF第二稳定性理论：对给定的ISF和定常ISF方程组解及x＝x0位置的“初始”扰动，若非湍流扰动运动（u′，p′），即定常ISPF方程组（5-6）或式（7-8）的解随流动向下游（x＞x0）发展而衰减或放大，则称ISF层流基本流分别为稳定或不稳定。

（1）ISF稳定性理论是一全新的课题，故需作一些必要的讨论。

由于ISF包含许多近壁局部区域ISF和节1所说的大范围ISF，所以ISF稳定性分析涉及许多丰富的研究内容，例如驻点邻域ISF稳定性、经典边界层与其无粘外流组成的ISF的稳定性，分离点邻域ISF和再附点邻域ISF稳定性，圆筒内、外顺轴向ISF稳定性、高超和超声速尖前缘和钝前缘平板、尖细长锥和小钝头细长锥高超声速绕流激波和壁面之间ISF的稳定性等等。这些无疑都超出了粘性边界层稳定性理论的范围。因此，需要实验的研究和理论分析计算，需要熟习节1和节2中研讨的ISF理论和ISPF理论以及求解PNS和PSE方程的数值方法。

上述ISF稳定性分析，无疑具有重要的理论基础意义和工程应用价值。稍加考虑即可列举出许多有意义的例子，例如圆筒内顺轴流，O.Reynolds在1883年经典实验中测出的转捩临界Reynolds数后经实验测定多次加以改进和完善，然而迄今未看到相应的理论分析和计算结果。又如高超和超声速尖前缘和钝前缘平板、尖细长锥和小钝头细长锥绕流ISF稳定性分析，获得非湍流扰动运动演化历程并结合实验资料预测转捩位置，无疑是迫切的工程需求，这种激波很贴近壁面的复杂干扰流动中往往边界层不明显甚至不存在。又如驻点邻域ISF，分离点邻域ISF和再附点邻域ISF稳定性分析，自然是具有流体力学基础意义的新课题。显然ISF稳定性理论能够分析和计算上述这些新课题。

（2）对ISF第一稳定性理论，当沿用边界层稳定性理论［3］，采取模（mode）-振幅函数分析方法时，需要找出ISF振幅函数满足的广义Orr-Sommerfeld（OS）方程并进行相应的特征值问题求解、研究初始稳定、二次稳定、中性稳定曲线、中性稳定Reynolds数、放大因子、及局部扰动波包（wave-packets）理论等。

已知利用PSE即ISPF方程组求解的模-振幅函数方法，分析计算粘性/无粘无干扰和弱干扰ISF粘性层（即边界层流）中非湍流扰动运动的演化及转捩发生的结果是DNS结果的合理近似。但是对粘性/无粘强干扰ISF，例如三层干扰流动［3］，它的流向和法向长度尺度仅为Re-3/8和Re-5/8或更小［3，17］。对强干扰ISF，尚未看到PSE即ISPF方程组的模-振幅函数方法的求解，这是有待发展的研究。由于ISF粘性层和ISPF粘性扰动层具有同一的空间尺度结构［18］，故在强干扰的流向小尺度区域，物理量（如壁面热流等）及非湍流扰动量都将发生局部“突增”现象。在高超声速绕流中，壁面热流等局部突变是引起飞行器局部受损的严重气动现象［26］；非湍流扰动量的局部突增无疑与转捩密切相关，往往直接导致转捩［3］。因此，对ISPF即PSE的求解不论采用模-振幅函数方法还是用原始扰动变量方法，以及对ISF即PNS方程的求解，都应关注和保证ISF强干扰区求解的有效性问题。如上所述强干扰区涉及的流向长度仅约LRe-3/8，与L相比很小，但它们对壁面热流突增、发生转捩的计算至关重要；这样才能保证在复杂ISF的整个流动区域，ISF即PNS的结果与NS的结果很好的相符，因此保证了在复杂ISF的整个层流流动区域ISF（即PNS）方程组解加上ISPF（即PSE）方程组解是ISF的DNS的合理近似。

（3）关于ISF第二稳定性理论，根据ISF粘性剪切层数学定义式（1）和（2）及连续性方程推知，粘性层切向特征流速u远大于法向特征流速v，x方向的长度尺度远大于法向长度尺度，因此分析和计算非湍流扰动运动沿x方向的演化具有物理意义，现在虽然还未看到这样的数值计算，但可推断这样的计算可行且有效。已知文献上不论对ISF（即PNS）方程组的求解，还是对ISPF（即PSE）方程组的求解，在流向马赫数大于1的条件下都采用空间推进求解的有效计算方法，而且数值结果丰硕，求解技术众多［9-13，19-21］。因此可以合理推断：由于ISPF粘性扰动层与ISF粘性层存在同一的空间尺度结构［18］，因此在与ISF（即PNS）方程组计算网格设计大体一致的粗网格下，人们能够有效地求解ISPF（即PSE）方程组，获得ISF层流中非湍流扰动运动，如对不可压缩流即u′和p′的演化历程，结合实验资料并可预测转捩位置。PSE分析边界层稳定性的众多有效的计算实践亦为人们能够有效求解ISPF方程提供了有力的旁证。关于ISF第二稳定性理论的进一步讨论与对第一稳定性理论讨论一致，这里不再重复。

（4）关于ISF稳定性理论的重要性问题，已有流动转捩位置的理论加经验预测均基于边界层稳定性理论，然而转捩并非总是最早发生在粘性边界层中，边界层仅是ISF粘性层的一小段，因此已有预测转捩位置的边界层理论计算方法局限性很大。流动转捩总是发生在ISF层流中，如上所述ISF包含了众多具有基础意义和工程应用价值的粘性-无粘流动，经典边界层加上它的相邻无粘外流仅是ISF的一个典型特例。可见，ISF稳定性理论提供了更好、覆盖面更宽广的预测转捩位置的理论计算方法，而且ISF稳定性理论的结果自然也包含了边界层稳定性理论的结果在内，因此对层流-转捩-湍流全程流动计算具有重要的理论意义和应用价值。

4 ISF稳定性理论的推论

推论1：干扰剪切扰动流（ISPF）即PSE方程组计算结合实验资料提供了预测ISF层流转捩位置的理论计算方法。

讨论：参考边界层稳定性理论预测转捩的研究［3-13］，预测ISF转捩位置除了计算ISPF方程组外，还需要根据具体ISF的转捩实验数据确定扰动量的时间放大程度（如eN方法中的N值）和空间放大程度与转捩位置的定量关系。因此不论根据时间放大还是空间放大来确定ISF转捩位置都具有经验性，也没有对所有ISF都适用的通用性质。但是，由于ISF，高Re数内外绕流近壁粘性/无粘层流是比边界层更宽广的重要流动现象，因此ISF稳定性理论开辟了流动稳定性研究的新课题和新领域，ISF稳定性理论的结果也包含了边界层稳定性理论的结果在内，对它的实验研究和理论分析计算因此值得关注和重视。由于粘性边界层加上它的相邻无粘外流是ISF的一个典型特例，因此ISF稳定性研究完全可以参考和借鉴边界层稳定性理论的有关研究。

推论2：ISF（即PNS）和ISPF（即PSE）方程组粗网格下的计算结果可合理近似ISF转捩前DNS的结果。

文献上的已有计算结果和节2与节3的分析讨论说明：对ISF、对高Re内、外绕流近壁粘性/无粘层流，ISF（即PNS）方程组数值结果与NS结果很好相符，关于边界层非湍流扰动运动演化，ISPF（即PSE）方程组的计算结果与DNS的结果很好相符，关于ISF非湍流扰动运动演化，可以预期ISPF（PSE）方程组计算将得到类似的结果，因此推论2成立。值得强调，在计算机时代，发展这样的近似方程理论，即在粗网格条件下计算它们可合理近似转捩前DNS的方程理论，具有重要的理论意义和工程价值；近似方程理论既能满足工业标准计算的需求，且在一定程度上能够揭示流动机理。目前看来，推论2还是合理简单且唯一的近似方程理论，对唯一近似方程理论的重要性有必要进一步加以强调，这是因为边界层稳定性理论不能解决ISF的稳定性问题；而层流DNS虽然比湍流DNS的耗费少很多，但由于转捩处物理量及其扰动量的变化梯度大，因此以转捩处为下游边界的层流DNS并不可能；转捩前层流的DNS只能与更远下游的湍流DNS一同求出。基于相同的理由，以转捩处为下游边界的层流基本流NS方程组求解以及扰动流NS扰动方程组的数值求解也没有可能。此外对工业标准气动计算，即使在DNS时代，RANS方法仍是一种有用的方法。因此对高Re数内外绕流计算，ISF加ISPF方程组可能是长期有用的近似方程理论，只要RANS方程有用，该近似方程理论就有用；对于转捩后的湍流现在没有、作者认为未来也不可能有这样的近似方程理论，由于湍流脉动在时间和空间上都具有杂乱无章和随机性特性，因此难以提出湍流脉动运动的演化方程，人们只好对湍流做时间平均和空间滤波运算，得到RANS和大涡模拟（LES）方程，再补充Reynolds应力模型和亚格子应力模型以封闭RANS和LES，获得湍流时间平均流动和大涡运动，这可看作是合理近似湍流DNS的另一种形式的近似方程理论；很显然RANS、LES、RANS/LES等就是这样的近似方程理论。应该提到，湍流DNS给出的也是最小尺度（Kolmogoroff尺度）网格下的湍流统计平均流动。

5 ISF稳定性理论和推论的应用

现今不论是工业标准气动计算基础的传统PNS方法，还是广泛应用的湍流RANS、RANS/LES等方法（统称RANS方法），都存在一个不足，即对层流-转捩-湍流全程高Re数流动计算、层流计算和转捩位置的确定是至今仍未很好解决的难题。

推论1和推论2与传统抛物化NS（PNS）方法和流行的湍流RANS方法相结合，这两个方法均将得到实质性的改进。现今得到广泛应用、已成为工业标准气动计算基础的传统PNS方法［2，19-25］运算为：ISF（即PNS）方程组计算加上基于边界层稳定性计算结合实验资料预测转捩位置，转捩后进行干扰剪切湍流（ISTF）（即PRANS）方程组计算。

推论1和推论2把传统PNS方法改进为如下的运算：

ISF（即PNS）和ISPF（即PSE）方程计算结合实验资料并确定转捩位置，转捩后为ISTF（即PRANS）方程计算。

这里PRANS为抛物化RANS。

流行的湍流RANS方法运算为：RANS和NS计算加边界层稳定性计算结合实验资料预测转捩位置，转捩后进行RANS、RANS/LES等方程组计算。

推论1和推论2把流行的RANS方法改进为：

ISF（PNS）和ISPF（PSE）方程组计算结合实验资料确定转捩位置，转捩后为RANS、RANS/LES等方程组计算。

显然，改进后的两方法与传统PNS方法和流行的湍流RANS方法相比，最大的特点是避免了根据边界层稳定性计算结合实验资料推算转捩位置的处理。边界层与ISF（对PNS方法）和近壁NS流（对RANS方法）不一致，边界层只是ISF粘性层和近壁NS流粘性层中的局部流动区域。边界层稳定性计算必须首先在ISF或近壁NS流中找到边界层，然后求解边界层方程组及其稳定性方程，更大的问题是我们不知道转捩是否最早发生在边界层中，也不知道ISF、近壁NS流中是否存在边界层。总之根据边界层稳定性理论预测转捩的方法，边界层与ISF或近壁NS流不一致，边界层方程与ISF方程和NS方程不一致，对边界层的计算其实是额外的计算，且值得怀疑的问题不少。相反根据ISPF（即PSE）方程组计算预测转捩位置的方法，它算出的是ISF中非湍流扰动的演化历程，ISF扰动流与ISF基本流完全一致，ISPF与ISF方程组相匹配，特别是转捩总是最早发生在ISF中。改进后的两方法在转捩前都是计算ISF和ISPF方程，这是ISF层流区DNS的合理近似，在转捩后是计算PRANS（对PNS方法）或是计算RANS、RANS/LES方程（对RANS方法），这是ISF湍流区DNS的合理近似，因此是高Re数流动计算的理想方法，且是可持续发展的两方法，因为不论合理近似层流DNS，还是合理近似湍流DNS，不论转捩的实验和理论分析计算，还是湍流Reynolds应力模型和亚格子尺度应力模型，以及计算能力的提高，都有不断改进的余地和需求。

最后提到，在改进后的RANS方法中，对近壁粘性/无粘层流及其扰动流的计算使用ISF和ISPF方程组，且如节4所述不能使用NS方程组和相应的NS扰动运动方程组；由于ISF是近壁NS层流的很好近似，ISF方程组是近壁NS方程组的很好近似；而且ISF和ISPF方程组数学上均为抛物型，对它们的求解不论是空间推进求解还是时间相关求解，都不需要规定下游边界条件，大大简化了转捩前层流流动的计算；相反用NS或RANS方程组计算转捩前的层流流动时，由于不能在转捩处设置下游边界条件而必须并把下游边界放在转捩后流动沿流向变化缓慢的区域，计算实际上已成为层流加湍流的DNS，无疑增加了计算的困难和麻烦。特别是对超声速和高超声速绕流，不论对ISF（即PNS）方程组还是对ISPF（即PSE）方程组，均可实施高效的单次空间推进求解，计算维数减少一维，是理想的气动快速算法。

6 结束语

高Re数流动计算是科学问题，更是众多工程技术领域的重大需求。计算需要的湍流模型已有广泛的研究和应用，需要的流动转捩位置理论预测均基于边界层稳定性理论，然而转捩并非总是最早发生在粘性边界层中，且有些内、外绕流的层流区域边界层现象可能不明显甚至不存在，因此已有预测转捩位置的计算方法局限性很大。流动转捩总是最早发生在干扰剪切流（ISF）中，ISF包含了众多具有基础意义和工程应用价值的粘性-无粘流动，经典边界层加上它的相邻无粘外流仅是ISF的一个典型特例。显然ISF稳定性理论是一个新课题，是流动稳定性的新开拓，该课题的实验研究和深化、干扰剪切扰动流（ISPF）方程即PSE的有效求解，必将导致已有的高Re数流动计算方法：传统PNS方法和湍流RANS方法的实质性改进。改进后的两方法在转捩前都是计算ISF-和ISPF-方程体系，得到的是层流DNS的合理近似，转捩后是湍流DNS的合理近似，方程体系完备、自洽，除需补充湍流模型外，不需要人为假定或根据边界层稳定性理论经验估算转捩位置，是粗网格下计算高Re数流动的理想且可持续发展的方法；特别是只要RANS方法有用，ISF和ISPF近似方程理论就有用处。进而考虑到湍流DNS给出的最完美结果是最小尺度（Kolmogoroff尺度）网格下的湍流统计平均流动，因此改进后的PNS方法和RANS方法很有可能引领未来的工业标准高Re数流动计算研究。

［1］ Spalart P R.Strategies for turbulence modeling and simulations［J］.Inter.J.of Heat and Fluid Flow，2000，21：252-263.

［2］ Anderson J D Jr.Hypersonic and high-temperature gas synamics［R］.2nded.，AIAA Education Series，2006.

［3］ Schlichting H，Gersten K.Boundary-layer theory［M］.Springer 2000.

［4］ Luo Jisheng，Shen Qing，Yang Wubin.Transition and its prediction of compressible shear-layer flow［M］//Fluid Dynamics.Beijing：Scientific press of China，2014：72-94.（in Chinese）罗纪生，沈清，杨武兵.可压缩剪切层的转捩及其预测［M］//流体动力学.北京：科学出版社，2014：72-94.

［5］ Walters D K，Leylek J H.A new model for boundary layer transition using a single-point RANS approach［J］.J.Turbomach，2004，126：193-302.

［6］ Wang Liang，Fu Song.A turbulent-flow transition model suitable to supersonic boundary flows［J］.Acta Mechanica Sinica，2009，42（2）：162-168.（in Chinese）王亮，符松.一种适用于超声速边界层的湍流转捩模式［J］.力学学报，2009，4（2）：162-168.

［7］ Reda D.Review and synthesis of roughness-dominated transition correlation for reentry applications［J］.J.Spacecraft ＆Rockets，2002，39（2）：161-167.

［8］ Kong Weixuan，Gao Ruizhe，Yan Chao.Hypersonic boundary layer transition prediction by empirical transition criteria［C］//The proceeding of 15thNational Computational Fluid Mechanics Conference，Shandong，2012：164-169.（in Chinese）孔未萱，高瑞泽，阎超.经验转捩准则对高超声速从边界层转捩的预测［C］//第十五届全国计算流体会议论文集，山东烟台，2012：164-169.

［9］ Su Caihong，Zhou Heng.Transition prediction of hypersonic sharp cone boundary layer flow with small angle of attack and improvement of eNmethod［J］.Science in China（Series G），2009，39（1）：123-130.（in Chinese）苏彩虹，周恒.小攻角高超声速尖锥边界层的转捩预测及eN方法的改进［J］.中国科学（G辑），2009，39（1）：123-130.

［10］Herbert T.Parabolized stability equations［J］.Annu.Rev.Fluid Mech.，1997，29：245-283.

［11］Chang C.The Langley stability and transition analysis code（lastrac）；1st，linear and nonlinear PSE for 2D，axisymmetric and infinite swept wing boundary layer［R］.AIAA 2003-974，2003.

［12］Choudhari M，Chang C L，Jentink T，et al.Transition PSE analysis for the HIFiRE-5vehicle［R］.AIAA 2009-4056，2009

［13］Hu S H，Zhong X.Nonparallel stability analysis of compressible boundary layer using 3-D PSE［R］.AIAA 99-0813，1999.

［14］Gao Zhi.Viscous-inviscid interacting flow theory［J］.Acta Mechanica Sinica，1990，6（2）：102-110.

［15］Gao Zhi.Interacting shear flow（ISF）theory，diffusion parabolized NS equations and wall-surface criteria and the applications［J］.Chinese Mechanics Abstracts，2007，21（3）：13-22.（in Chinese）高智.干扰剪切流（ISF）理论、扩散抛物化NS方程组和壁面判据及它们的应用［J］.中国力学文摘，2007，21（3）：13-22.

［16］Gao Zhi.Interacting shear flow（ISF）and boundary-layer flow and applications of ISF theory in computational fluid dynamics［J］.Advances in Mechanics，2008，38（1）：114-116.（in Chinese）高智.干扰剪切流动（ISF）和边界层流动及ISF理论在计算流体力学中的应用［J］.力学进展，2008，38（1）：114-116.

［17］Gao Zhi.Strong viscous layer flow theory with application to viscousflow computation［J］.Acta Aerodynamica Sinica，2001，19（4）：420-426.（in Chinese）高智.强粘性层流理论及在粘性流计算中的应用［J］.空气动力学学报，2001，19（4）：420-426.

［18］Gao Zhi.Invariance of interactive-structure between convection and diffusion［J］.Acta Mechanics Sinica，1992，24（6）：661-670.（in Chinese）高智.对流扩散相互作用结构的不变性［J］.力学学报，1992，24（6）：661-670.

［19］Rubin S G，Tannehill J C.Parabolized/Reduced Navier-Stokes computational techniques［J］.Annu.Review Fluid Mech.，1992，（24）：117-139.

［20］Tannehill J C，Anderson D A，Pletcher R H.Computational fluid mechanics and heat transfer［M］.2nded.New York：Hemisphere press，1997.

［21］Yu Y.Review on Parabolized Navier-Stokes（PNS）equations and Gao’s PNS theory with inferences and applications［J］.Acta Aerodynamica Sinica，2015，33（1）：54-65.

［22］Li G B，Dai M G，Gao Z.An application of interacting shear flows（ISF）theory：exact solution for unsteady oblique stagnation point-flow［J］.Acta Mechanica Sinica，2006，22：397-402.

［23］Baldwin B S，Lomax H.Thin-layer Navier-Stokes approximation and algebraic model for separated turbulent flows［R］.AIAA 78-0257，1978.

［24］Blottner F G.Significance of the thin-layer Navier-Stokes approximation［M］//Cebeci T.Numerical and physical aspects of aerodynamic Flows.New York：Springer-Verlag，1986：184-205.

［25］Zhuang Fenggan，Zhang Deliang.Significance of diffusion-parabolized NS equations and its application to computational fluid dynamics［J］.Acta Aerodynamica Sinica，2003，21（1）：1-10.（in Chinese）庄逢甘，张德良.扩散抛物化（DP）NS方程组的意义及其在计算流体力学（CFD）中的应用［J］.空气动力学学报，2003，21（1）：1-10.

［26］Bertin J J，Cummings R M，Critical hypersonic aerothermodynamics phenomena［J］.Annu.Rev.Fluid Mech.，2006，38：129-157.

［27］Herbert T H，Bertoloti F P.Stability analysis of non-parallel boundary layer［J］.Bull.Am.Phys.Soc.，1987，32：2097-2806.

［28］Chang C L.The langley stability and transition analysis code（LASTRAC）Part 1LST，linear and nonlinear PSE for 2D，axisymmeteric and infinite swept wing boundary layers［R］.AIAA 2003-0974.

Interacting shear flow stability theory with application to improving computational method of simulating numerically high Reynolds number flows

Gao Zhi
（State Key Laboratory of High Temperature Gas Dynamics，Institute of Mechanics，Chinese Academy of Science，Beijing 100190，China）

On the basis of the interacting shear flow（ISF）theory proposed by the author，the ISF stability theory and its two inferences with application to improving computational methods of simulating numerically high Reynolds（Re）number inner/outer flows are presented in this paper.（1）In the RANS computations and an industry-standard PNS computations for high Reynolds number flows over bodies，predicting transition is always based on the classical boundary-layer theory coupled with experimental data；however，transition does not always occur originally in boundary-layer，initial transition may occur in dents，or small step or small cracks at wall，these local strong interaction flow regions may locate in boundary layer，but boundary-layer theory is not suitable for these flow regions，and transition occurs in strong interaction flow region near separation point etc.（2）Flow transition occurs always in interacting shear flow，ISF theory extracted by the author is composed of viscous shear layer and its neighbor outer inviscidflow with interaction each other；ISF summarizes many viscous-inviscid flows with basis meanings and engineering values，two typical example of ISF are the classical viscous boundary layer added its neighbor outer inviscid flow，and the viscous/inviscid flow near wall in highRenumber inner/outer flows over bodies.（3）The interacting shear perturbed flow（ISPF）equations offer new theoretical computational method to simulate non-turbulence perturbed motion and transition in ISF.The ISF-equations and ISPF equations are respectively the same kind of PNS-and PSE-equations.Many works of using PSE analyses and computes boundary-layer stability show that it is perfectly feasible to compute perturbed flow of ISF and predict transition using ISPF（or PSE）equations.（4）The computational results given by solving simultaneously ISF-and ISPF equations are reasonable approximation of the direct numerical simulation（DNS）of ISF before transition.（5）Integrating the ISF stability theory and its two inferences with both of the traditional PNS method and the current RANS，RANS/LES methods（call them RANS method unitedly here）leads to several substantial improvements of this two methods.Such as，avoiding artificial assumption of transition location or estimating experientially transition location on the basis of the boundary layer stability theory etc..Both of improved PNS-and RANS-methods compute simultaneously ISF-and ISPF-equations，that provide reasonable approximation of direct numerical simulation（DNS）of ISF before transition；after transition the improved PNS method computes parabolized RANS（PRANS）equations and the improved RANS method computes RANS，RANS/LES equations and both of this two calculations provide reasonable approximation of statistical average flow given by DNS of interacting shear turbulent flow.（6）In the improved these two methods，equation system is perfect and self-affirming，therefore they are ideal methods for computing highRenumber inner/outer flows over bodies and would have broad prospects of development and application.

high Reynolds number flow；PNS method；RANS method；interacting shear flow（ISF）theory；ISF stability theory

V211.3

：Adoi：10.7638/kqdlxxb-2014.0098

0258-1825（2015）02-0183-09

2014-09-17；

：2015-01-11

国家自然科学基金（11272324）

高智＊（1937-），研究员，主要从事流体力学，计算流体力学研究.E-mail：gaozhi＠imech.ac.cn

高智.干扰剪切流动稳定性理论及其对高雷诺数流动数值模拟方法的改进［J］.空气动力学学报，2015，33（2）：183-191.

10.7638/kqdlxxb-2014.0098 Gao Z.Interacting shear flow stability theory with application to improving computational method of simulating numerically high Reynolds number flows［J］.Acta Aerodynamica Sinica，2015，33（2）：183-191.