基于综合安全系数的强度折减法的改进

王强志 高永涛 吴顺川 张华恺 杨 凯

(1.北京科技大学土木与环境工程学院，北京100083;2.金属矿山高效开采与安全教育部重点实验室，北京100083;3.中电建路桥集团有限公司，北京100048)

边坡破坏是一个渐进累积的过程，由局部破坏逐渐扩展至贯通形成滑裂面。在该过程中，由于土体含水量变化、蠕变和化学潜蚀等，土体强度参数逐渐降低，但c 和φ的衰减程度和衰减速度是不相同的，且较大程度上取决于土体物理性质。因此，在边坡失稳破坏过程中，c 和φ的安全储备是不相同的。一般认为，在边坡失稳过程时，剪切带的形成与土体的应变软化相关。沈珠江［1］将土体的应变软化分为3 种:损伤软化、剪胀软化以及减压软化。黏性土的软化时由于其结构破坏，黏聚力迅速衰减，主要表现为损伤破坏;砂土软化时由于孔隙增大，内摩擦角会迅速降低，主要表现为剪胀软化。

近年来，边坡数值模拟技术得到了长足的发展，吴顺川、杨光华等［2-7］基于有限差分原理进行边坡稳定性分析，并验证了其合理性，但其在折减过程中，c和φ均采用同一折减系数，而根据潘家铮最大、最小值原理［8］，边坡发生滑动时，滑动面上内力会自发的进行调整以发挥最大的抗滑能力，若c 和φ采用同一折减系数，这与实际情况是不相符的。唐芬等［9-11］提出了土坡渐进破坏的双安全系数，并指出:在黏土边坡中，SRFc＞SRFφ(SRFc为c 的折减系数，SRFφ为 φ的折减系数)，而在砂土边坡中，SRFc＜SRFφ，但未明确提出c 和φ折减系数之间的关系，且其定义的综合安全系数只是将c 和φ的安全储备取平均值，这与工程实际差异较大。

根据Mohr－Coulomb 屈服准则，基于强度储备原理，本研究提出更为合理的边坡综合安全系数。通过对土体应变软化特性进行分析，假定强度参数在软化过程中服从线性衰减，推导出c 和φ折减系数之间的关系，并通过算例验证该折减方案的合理性。

1 边坡综合安全系数的提出

1.1 边坡双安全系数

边坡发生失稳破坏时，滑动面土体的黏聚力和摩阻力发挥的作用、发挥的程度均不尽相同，因此，为了更加准确地反映c 和φ各自的安全储备，在强度折减法中，c 和φ应该拥有不同的折减系数，即双折减系数，对应边坡极限状态下的双折减系数即为双安全系数:

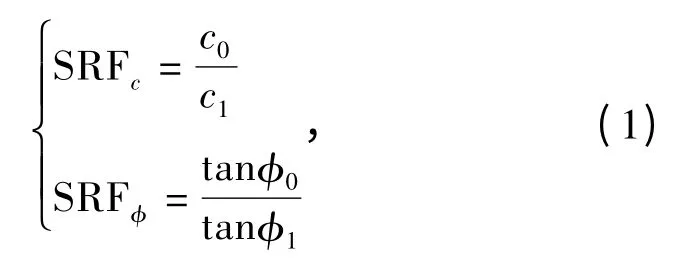
其中，c0、φ0分别为黏聚力和内摩擦角折减初值，c1、φ1分别为极限平衡状态下的黏聚力、内摩擦角，SRFc和SRFφ即为双安全系数。

为体现边坡失稳过程中c、φ衰减速率的不同，定义强度参数折减比λ，简称折减比，如式(2)所示，若λ 越大，则c 的衰减速率就越快:

D.W.Taylor 首先在摩尔圆分析法中针对c、φ采用不同的安全系数，认为边坡发生滑动时，滑动面上摩阻力首先得到充分发挥，然后才由土的黏聚力作补充［12］。因此，他将边坡的安全系数定义为滑面土体实际的黏聚力与为使边坡达到极限平衡时滑动面上所需要发挥的黏聚力的比值，此安全系数定义隐含了SRFφ=1这显然与滑动面土体应变软化的试验结果尤其是砂土软化试验结果存在分歧。

在实际工程中，当采用双安全系数进行边坡稳定性评价时，需解决以下2 个主要问题［13］。

(1)采用何种参数来表征边坡的安全储备。由于工程实际通常采用单一参数评价边坡安全储备情况，因此需要选用一种综合参数来评价边坡稳定性，即

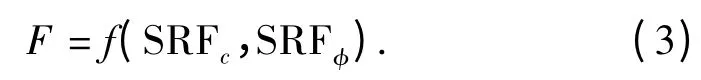
(1)强度折减系数之间的关系，即:

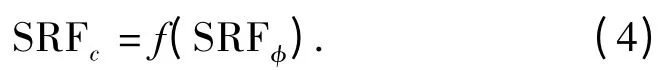
1.2 综合安全系数的定义

边坡双安全系数虽然体现了在边坡失稳过程中c 和φ所起的不同作用，但其在衡量边坡稳定性方面缺乏统一的标准，岩土工作者通常习惯用1 个安全系数来判断边坡的稳定性。本研究根据滑动面土体极限状态下的Mohr－Coulomb 屈服准则，基于强度储备原理，尝试提出一种边坡综合安全系数的定义。

滑动面的抗滑力通常由2 部分构成，一部分是土体本身提供抗滑力，另一部分则是外部加固作用，如锚杆、抗滑桩等的加固力。综合安全系数定义为边坡土体强度参数折减前滑动面提供的抗滑力与极限状态下滑动面提供的抗滑力的比值，即

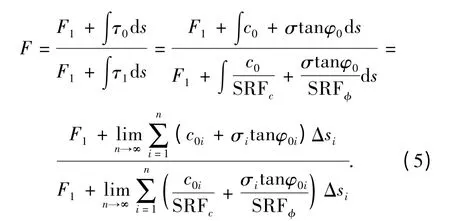
其中，F1为滑动面的加固力，c0i、φ0i分别为滑动面各土条的初始黏聚力和内摩擦角，σi、si分别为极限状态下各土条底部的正应力和长度。潜在滑动面可由slope/W 软件确定。

传统强度折减法将边坡达到极限平衡状态时强度参数的折减系数作为边坡的安全系数，而当c 和φ进行非等比折减时，其在判断边坡失稳方面存在不确定性。本研究提出的综合安全系数将传统安全系数的定义运用到强度折减法中，既可以体现c 和φ在边坡失稳过程中所起的不同作用，也克服了双安全系数的不确定性。

2 强度折减法的改进

在边坡失稳破坏过程中，潜在滑动面上应力和应变分布是不均匀的，在外部因素作用下，局部区域的剪力超过其抗剪强度或应变超过一定值，土体将进入软化阶段，抗剪强度衰减，原本由这些区域承受的部分剪力转移到周围的土体，进而可能使周围土体也进入软化阶段［14］。如果不断推进则可能形成剪切带，最终导致边坡的失稳破坏。1948 年，Terzaghi 等在边坡工程中发现土体应变软化在宏观上表现为边坡渐进累积破坏，而其根本原因在于土体抗剪强度从峰值强度降低为残余强度。土体的应变软化曲线如图1 所示。

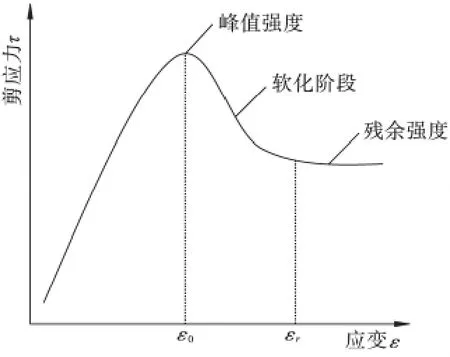
图1 土的应变软化曲线Fig.1 Soil softening curve

Conte 等［15-16］在分析边坡稳定性时，假设土软化过程中，强度参数c、φ由初始值c0、φ0同步线性折减至残余强度参数cr、φr边坡达到极限平衡状态时的应变为ε1，且ε1∈(ε0，εr)，此时对应的强度参数为c1、φ1，如图2 所示。

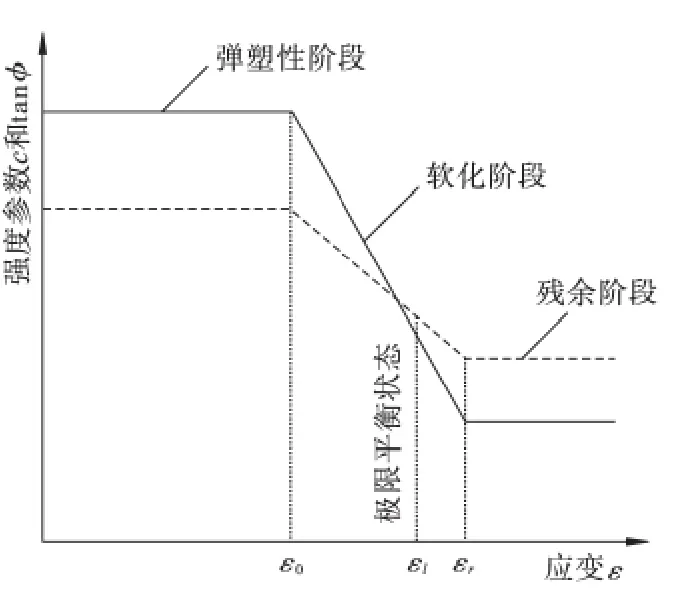
图2 强度参数在软化过程中的变化Fig.2 Variation of strength parameters in soil softening process

根据强度参数衰减过程中，其衰减速率保持不变的规律，可以得到如下结果:

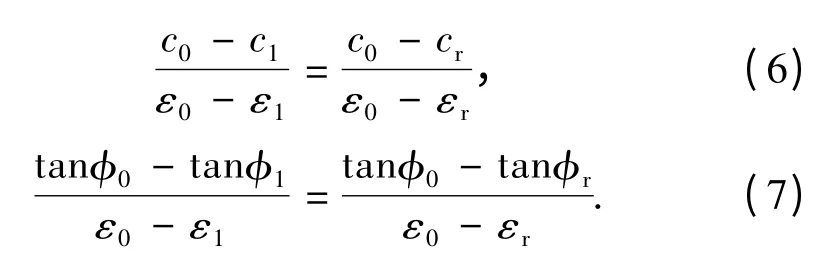
对式(6)和式(7)变形可得

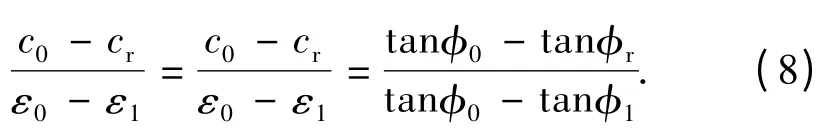
将式(1)代入式(8)中，有

令

则

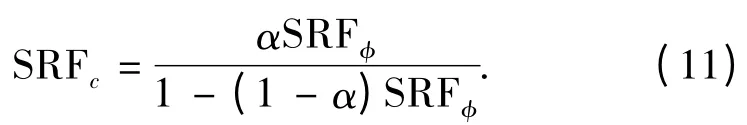
α 可通过土工试验获得，因此在强度折减过程中，折减参数SRFc、SRFφ之间的关系可按式(11)进行确定，双安全系数变成了单一安全系数的确定，克服了传统强度折减法无法考虑土体劣化过程的缺点和双安全系数的盲目性。

3 算 例

利用FLAC3D中的fish 语言，编写自定义强度折减程序，实现强度参数c、φ非等比折减。

3.1 模型构建

边坡模型参数来自重庆某路堑土质边坡，模型总高度为25 m，总宽度为40 m，坡脚至模型前缘的距离为15 m，坡顶到模型后缘的距离也为15 m，坡高10 m，坡度45°，γ=19.8 kN/m3，E=50 MPa，μ=0.4，c0=29.8 kPa，φq=10.3°，cr=11.5 kPa，φr=8.4°模型如图3 所示。

图3 边坡模型Fig.3 Schematic diagram of slope model

3.2 计算过程

在边坡失稳破坏过程中，有2 种比较极端的情况，一种是黏聚力先充分发挥作用，然后才由摩阻力作为补充，即只折减φ、不折减c;另一种就是摩阻力先充分发挥作用，然后才由黏聚力作为补充，即只折减c、不折减φ。利用编写的自定义强度折减程序，首先只折减φ、不折减c，得到c 和φ折减系数，由式(5)可计算出最小的折减比λmin=0.223 下的综合安全系数;接着只折减c、不折减 φ，可得到最大的折减比λmax=1.539 下的综合安全系数。接着在(λmin，λmax)中均等地插入若干个λ 值，计算其相应的综合安全系数，结果如表1 所示。

从表1 可以看出，综合安全系数总体上随着折减比的增大而增大。因此，在黏土边坡失稳破坏的过程中，ε 所起的作用要大于 φ，即SRFc＞SRFφ据此可知，合理的折减比λ ∈(1，λmax)，传统强度折减法c和φ采用同一折减系数是不合理的，亟待进一步改善。

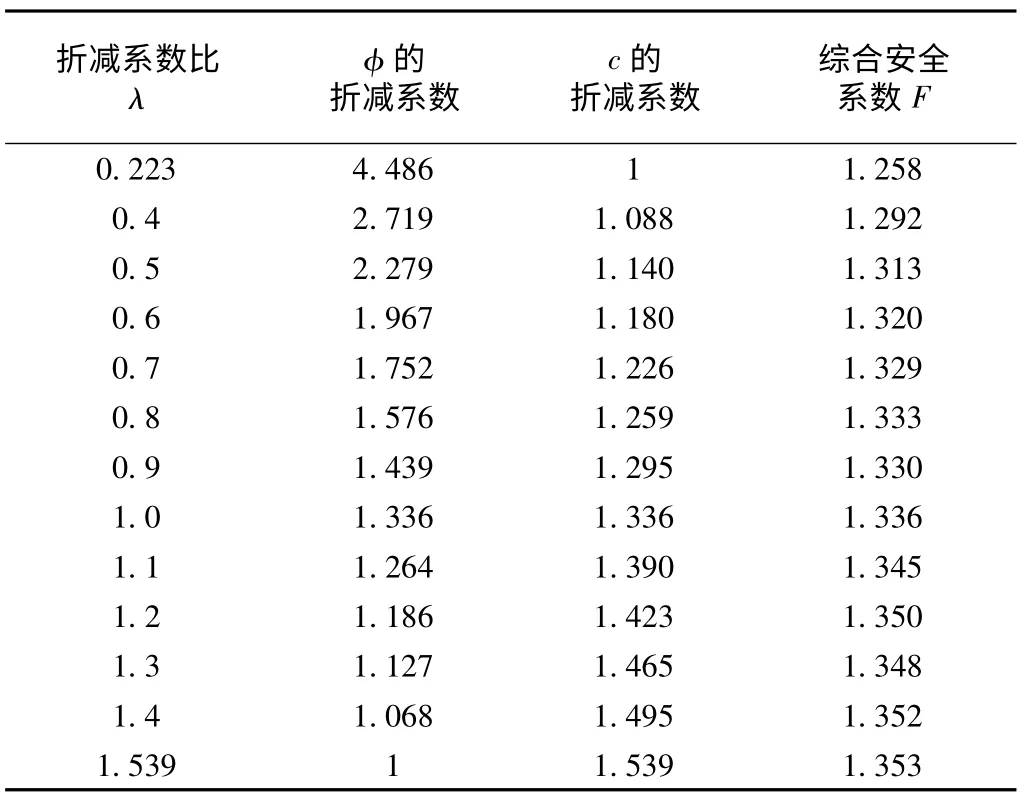
表1 不同强度参数折减比λ 下的综合安全系数Table 1 Comprehensive safety factor under different Strength reduction ratio

在边坡实际滑动过程中，摩阻力和黏聚力是共同发挥作用的，只是其发挥的作用和程度不尽相同。利用本研究提出的改进强度折减法进行计算，根据边坡土体的参数，由式(10)、式(11)得

将式(12)用fish 语言编入自定义折减程序中，求得SRFc= 1.464，SRFφ= 1.107，λ = 1.322，F =1.349。不同折减比λ 下的滑裂面形状如图4 所示，λ=1.322 时，即为改进强度折减法的潜在滑裂面。分析不同折减比下的滑裂面，随着折减比的增加，边坡滑裂面深度逐步减小，即其安全系数增大。

本研究提出的改进强度折减法计算出的折减比λ=1.322∈(1，λmax)，其安全系数为1.349，略大于传统强度折减法的安全系数1.336，滑裂面深度也小于传统强度折减法的滑裂面深度，如图4。因此，改进强度折减法是合理的，它克服了传统强度折减法低估边坡稳定性和双安全系数不确定性的劣势。

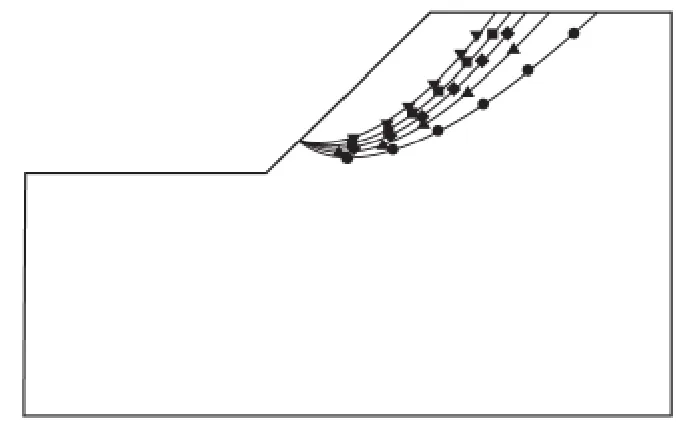
图4 不同强度参数折减比λ 下的潜在滑动面形状Fig.4 Slip surface shape under different strength reduction ratio

传统强度折减法提出的安全储备脱离土体实际劣化过程，定义使边坡达到极限平衡状态时的强度折减系数作为安全系数。本研究通过分析土体的软化特性，探讨了强度参数折减与土体性质劣化之间的关系，保证了边坡达到极限平衡状态时的强度参数位于初始强度参数与残余强度参数决定的直线上，即极限平衡状态时对应的强度参数在边坡强度参数的弱化路径上，因此，改进的强度折减法提出的安全储备更加符合实际情况。

4 讨 论

边坡失稳是一个十分复杂的过程，随着外部条件的改变，潜在滑动面土体强度从峰值强度降到残余强度是边坡发生破坏的根本原因。传统强度折减法对土体的强度参数c、φ采用同一折减系数，而在边坡实际破坏过程中，强度参数c、φ发挥的作用和程度是不相同的，因此，c、φ应具有不同的安全系数，即双安全系数，但双安全系数在衡量边坡稳定性方面缺乏统一标准，这是其无法被广泛应用的一个重要原因。基于边坡潜在滑动面抗滑力储备的基本原理，提出综合安全系数的概念，其充分考虑强度参数c、φ在抗滑力中的不同贡献值，克服了双安全系数无法判定边坡稳定性的缺陷。

影响双安全系数进一步推广的另一个重要原因为强度参数c、φ的折减过程具有盲目性，在此基础上得到的安全储备很难有说服力。通过分析土体应变软化特性，假定土体软化过程中，强度参数c、φ由初始值线性折减至残余值，推导得出SRFc与SRFφ之间的关系式，进而双折减系数变成单一折减系数的确定，同时也将土体的劣化过程与强度参数折减结合在了一起，提出的安全储备更有说服力。

强度折减法作为近几十年来一种方兴未艾的边坡稳定性分析方法，它有效避免了极限平衡方法提前假定滑裂面形状、无法考虑支护结构与土体之间的相互作用等一系列缺点。但其对强度参数c、φ都是按照线性同步折减，实际边坡失稳中，c 与φ发挥作用的先后顺序是有区别的，并且也不是按线性折减，这方面还需要广大学者展开进一步的研究。

5 结 论

(1)根据边坡滑动面土体极限平衡状态下的Mohr－Coulomb 屈服准则，基于强度储备原理，提出边坡综合安全系数的定义，克服了双安全系数在衡量边坡稳定性方面的不确定性等问题，有利于强度参数非等比折减方法在边坡稳定性分析中的进一步应用。

(2)通过分析不同强度参数折减比λ 下的综合安全系数，可以看出，在黏土边坡失稳破坏过程中，c所起的作用要大于φ，即SRFc＞SRFφ传统强度折减法中c 与φ采用同一折减系数是不太合理的。

(3)通过对边坡滑动面土体的软化过程进行推导，基于土体应变软化过程中强度参数c、φ同步线性折减的基本假定，确定SRFc和SRFφ之间的关系，对强度折减法进行了改进，克服了传统强度折减法无法考虑滑动面土体劣化过程等问题，计算得到的边坡安全系数相比传统折减法更加合理，能更好地指导实际工程实践。

［1］ 沈珠江.理论土力学［M］.北京:中国水利水电出版社，2000:19-23.

Shen Zhujiang.Theoretical Soil Mechanics［M］. Beijing:China Waterpower Press，2000:19-23.

［2］ 李 健，高永涛，吴顺川，等. 露天矿边坡强度折减法改进研究［J］.北京科技大学学报，2013，35(8):971-976.

Li Jian，Gao Yongtao，Wu Shunchuan，et al.Improvement research on the strength reduction method for open-pit mines［J］.Journal of University of Science and Technology Beijing，2013，35(8):971-976.

［3］ 杨光华，钟志辉，张玉成，等. 用局部强度折减法进行边坡稳定性分析［J］.岩土力学，2010，31(S2):53-58.

Yang Guanghua，Zhong Zhihui，Zhang Yucheng，et al.Slope stability analysis by local strength reduction method［J］. Rock and Soil Mechanics，2010，31(S2):53-58.

［4］ 刘 飞，胡 斌，宋 丹，等. 开挖扰动对露天矿边坡稳定性影响分析［J］.金属矿山，2013(12):111-114.

Liu Fei，Hu Bin，Song Dan，et al. Analysis of the impact of excavation disturbance on open-pit mining slope stability［J］.Metal Mine，2013(12):111-114.

［5］ 吴顺川，金爱兵，高永涛. 基于广义Hoek－Brown 准则的边坡稳定性强度折减法数值分析［J］. 岩土工程学报，2006，28(11):1975-1980.

Wu Shunchuan，Jin Aibing，Gao Yongtao.Numerical simulation analysis on strength reduction for slope of jointed rock masses based on generalized Hoek-Brown failure criterion［J］. Chinese Journal of Rock Mechanics and Engineering，2006，28(11):1975-1980.

［6］ 常来山，李 欣，牛文杰，等. 眼前山露天矿转地下开采边坡大变形模式数值模拟［J］.金属矿山，2013(12):31-32.

Chang Laishan，Li Xin，Niu Wenjie，et al. Numerical simulation of rock slope on large deformation mode for transition from Yanqianshan open-pit to underground mining［J］.Metal Mine，2013(12):31-32.

［7］ 张玉成，杨光华，胡海英，等. 利用变模量强度折减法计算结果确定土质边坡临界滑动面的方法［J］. 岩土工程学报，2013，35(S1):14-22.

Zhang Yucheng，Yang Guanghua，Hu Haiying，et al. Searching for critical slip surface in soil slopes based on calculated results by variable modulus elastoplastic strength reduction method［J］. Chinese Journal of Rock Mechanics and Engineering，2013，35(S1):14-22.

［8］ 陈祖煜.土质边坡稳定性分析［M］.北京:中国水利水电出版社，2003:86-120.

Chen Zuyu.Stability Analysis on Soil Slope［M］.Beijing:China Waterpower Press，2003:86-120.

［9］ 唐 芬，郑颖人.基于双安全系数的边坡稳定性分析［J］. 公路交通科技，2008，25(11):39-44.

Tang Fen，Zheng Yingren.Slope stability analysis based on two safety factors［J］.Journal of Highway and Transportation Research and Development，2008，25(11):39-44.

［10］ 唐 芬，郑颖人.强度储备安全系数不同定义对稳定系数的影响［J］.土木建筑与环境工程，2009，31(3):61-65.

Tang Fen，Zheng Yingren.Effect on safety factors in different definitions based on strength margin［J］.Journal of Civil Architectural＆ Environmental Engineering，2009，31(3):61-65.

［11］ 唐 芬，郑颖人，赵尚毅. 土坡渐进破坏的双安全系数讨论［J］.岩石力学与工程学报，2007，26(7):1402-1407.

Tang Fen，Zheng Yingren，Zhao Shangyi. Discussion on two safety factors for progressive failure of soil slope［J］. Chinese Journal of Rock Mechanics and Engineering，2007，26(7):1402-1407.

［12］ 洪毓康.土质学与土力学［M］. 北京:人民交通出版社，1979:189-193.

Hong Yukang.Soil Property and Soil Mechanics［M］.Beijing:China Communications Press，1979:189-193.

［13］ 赵炼恒，曹景源，唐高朋，等.基于双强度折减策略的边坡稳定性分析方法探讨［J］.岩土力学，2014，35(10):2977-2984.

Zhao Lianheng，Cao Jingyuan，Tang Gaopeng，et al. Discussion on slope stability analysis with double strength reduction technique［J］.Rock and Soil Mechanics，2014，35(10):2977-2984.

［14］ 郑颖人，赵尚毅.边(滑)坡工程设计中安全系数的讨论［J］.岩石力学与工程学报，2006，25(9):1937-1940.

Zheng Yingren，Zhao Shangyi.Discussion on safety factors of slope and landslide engineering design［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25(9):1937-1940.

［15］ Conte E，Silvestri F，Troncone A.Stability analysis of slopes in soils with strain-softening behavior［J］. Computers and Geotechnics，2010，37(5):710-722.

［16］ Conte E，Donato A，Troncone A.Progressive failure analysis of shallow foundations on soils with strain-softening behavior［J］.Computers and Geotechnics，2013，54:117-124.