DP工艺Inconel 718合金高温流变曲线修正及应变本构模型
司家勇 ,廖晓航,黄再旺,江 亮
(1. 中南林业科技大学 机电工程学院,长沙 410004;2. 中南大学 粉末冶金国家重点实验室,长沙 410083)
Inconel 718合金是一种铌强化的沉淀硬化型铁镍基高温合金,由于其优良的高温力学性能,在航空工业中被广泛用于制造一些关键零部件,如压气机盘、涡轮盘、轴和叶片等[1-3]。Inconel 718合金以体心四方结构的 γ″相(Ni3Nb) 为主要强化相, 同时辅以面心立方结构的弱强化相γ′(Ni3AlTi),正交结构的δ相(Ni3Nb)是γ″相的平衡相。Inconel 718合金的组织性能对热加工工艺很敏感,工艺控制不当会产生粗晶、混晶等现象,进而影响锻件的持久缺口敏感性和冲击韧度等[4]。由于Inconel 718合金中δ相通过钉扎晶界阻碍晶粒长大,目前开发了一种δ相时效处理(DP)工艺,即在变形前的合金中有意预析出δ相,通过控制热加工过程中的变形工艺来获取晶粒均匀细小且性能优良的锻件。RUIZ等[5]通过这种DP工艺获得了平均晶粒尺寸等级ASTM 8级的直径为150和200 mm的Inconel 718合金锻坯,以及晶粒尺寸等级为11级的直径为76 mm和38 mm的棒坯。DIX等[6]利用DP工艺获得了晶粒尺寸等级为9级的Inconel 718合金锻坯,并通过闭模锻造获得了晶粒尺寸为ASTM 13级的涡轮盘锻件。BHOWAL等[7]将Delta工艺和Gatorizing工艺相结合获得了晶粒尺寸等级高于ASTM 11级的Inconel 718合金涡轮盘锻件。吕宏军等[8]结合Delta工艺和轧制技术,可以得到ASTM 12~14级的超细晶粒组织Inconel 718合金板材。张海燕等[9-10]研究了Inconel 718合金等温压缩变形过程中δ相的演变机制,在变形断裂和溶解断裂的综合作用,片层/长针状δ相发生球化,转变为颗粒/短棒状δ相。YUAN等[11]对比了不同δ相含量对Inconel 718合金热变形行为的影响,结果显示,δ相的存在不仅会降低合金的峰值应变和峰值应力,而且可以促进峰值应力后的流变软化过程。WANG等[12-13]研究了δ相溶解行为及对变形机制的影响,高温变形时δ相主要以弯曲、扭折和切断等方式来协调塑性变形,并在界面能降低的驱动力下由针状逐渐转变为短针状乃至球状,其动态再结晶机制主要是δ相诱发动态再结晶形核和非连续动态再结晶形核。CONE等[14]也观察了不同形态δ相合金轧制过程中的δ相转变过程。但目前针对经DP工艺处理Inconel 718合金变形行为的研究较少,且未见有关变形过程中摩擦及温升效应等影响的相关报道,尚未建立适用于Inconel 718合金流变应力预测的准确本构模型[15-20]。
因此,本文作者通过热压缩实验分析δ相时效态Inconel 718合金的热变形行为,探讨压缩变形过程摩擦力和温度变化对实验获取的真应力-真应变数据的影响,对热压缩实验数据进行修正,进而引入应变量参数,建立预测精度较高的Inconel 718合金高温流变应力本构模型,可为经DP工艺处理的Inconel 718合金热加工参数的制定和优化提供依据。
1 实验
试验用材料为辽宁抚顺特钢公司生产的直径为200 mm的Inconel 718合金锻棒,其化学成分为(质量分数,%):C 0.036, Ni 52.12, Cr 18.75, Nb 5.36, Mo 2.99,Ti 1.00, Al 0.49, B 0.004, Si 0.10, Mn 0.02, Co 0.04, 余量为 Fe。对材料进行δ相时效处理,1040 ℃保温40 min水冷,目的是消除原始组织存在的偏析和残余应力、应变,并保证合金的显微组织为奥氏体固溶体和少量的碳化物,随后在900 ℃时效24 h析出一定量δ相,时效结束后水冷至室温,显微组织如图1所示。由图1可见,经δ相时效处理后,原始的奥氏体晶界已基本消失,合金的组织为魏氏体δ相组织,δ相主要存在于晶内,表现为大量片层状/长针状和少量颗粒/短棒状δ相,δ相的体积含量约为9.6%,经截线法测量平均晶粒尺寸约为 150 μm。将 DP工艺处理的Inconel 718合金机加工成d 10×15 mm的圆柱形热压缩试样,高温热压缩试验在计算机控制的 MTS力学试验机上进行,变形温度分别为900、940、980、1020和 1060 ℃,应变速率分别为 0.001、0.005、0.01、0.05、0.1和0.5 s-1,变形量为70%。热压缩试样达到指定变形量后,立即快速水淬冷却以保留其高温变形组织,将试验获取的压下量-载荷数据经过处理后得到材料的真应力-真应变曲线。采用电火花线切割将压缩后试样沿轴向切开,机械抛光后进行化学腐蚀,使用Leica光学显微镜和Quanta 650型扫描电镜进行试样显微组织观察。

图1 Inconel 718合金经DP工艺处理后的显微组织和δ相形貌Fig. 1 Microstructure and morphology of δ phase of Inconel 718 alloy after DP process: (a) Optical microstructure; (b) SEM image showing distribution of δ phase

图2 DP工艺Inconel 718合金高温热压缩曲线Fig. 2 True stress-true strain curves of delta-processed Inconel 718 alloy: (a) 900 ℃; (b)940 ℃; (c) 980 ℃; (d) 1020 ℃; (e) 1060 ℃
2 结果与分析
2.1 热压缩流变数据的修正
将通过热压缩实验获得的δ相时效态Inconel 718合金高温变形真应力-真应变曲线如图 2所示。对于单向压缩实验,影响实验精度的主要因素包括试样端面的摩擦力和试样的温度。理论上,只有试样均匀变形,压缩后试样中部无鼓度,实验过程中试样温度均匀一致,所测得的实验结果才能反映试样塑性变形过程的真实情况。但实际上由于摩擦的存在,试样在压缩过程总会出现鼓肚的现象,加上变形热效应的作用,试样温度也会有所变化,导致流变应力误差的产生,而且在高应变速率条件下温度所引起的应力误差会较大。因此,一般对于这两种原因引起的热压缩流变应力误差需进行修正。
2.1.1 压缩过程摩擦影响的修正
对于热模拟实验数据的摩擦修正,已有一些理论和实验研究。严巍等[21]引入平均等效应变的概念,利用有限元理论和逐步逼近的方法,得到最终的真应力-真应变曲线,但这种方法的摩擦因数均需另外测定。TSENG等[22]用鼓肚的体积与变形部分体积的比值定义鼓肚,由试样瞬时的高度、瞬时最大直径和瞬时最小直径来计算鼓肚形状的瞬时曲率半径,并提出修正系数方程,但如采用这种方法,测量试样的瞬时尺寸比较困难。许树勤等[23]结合有限元数值模拟方法,给出了不同变形温度和应变速率变形条件下镦粗摩擦因数与鼓肚的关系图,采用主应力法对应力-应变曲线进行修正,这种方法认为原始材料的影响较小。本研究中采用相对简便的根据变形功法推导的镦粗变形力公式来计算摩擦修正后的真应力(σf)[24]:
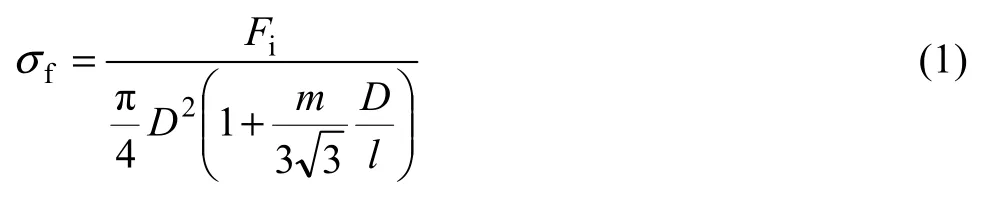
式中:Fi为实验机记录的瞬时载荷;D为试样瞬时直径;H为试样瞬时高度;m为摩擦因数。m的计算则采用 EBRAHIMI等[25]提出的能量法:在圆柱坐标系下,假设鼓肚形状为某圆周上的一段圆弧,通过对速度场的描述,由压缩后试样的高度和最大直径来反求摩擦因数,即
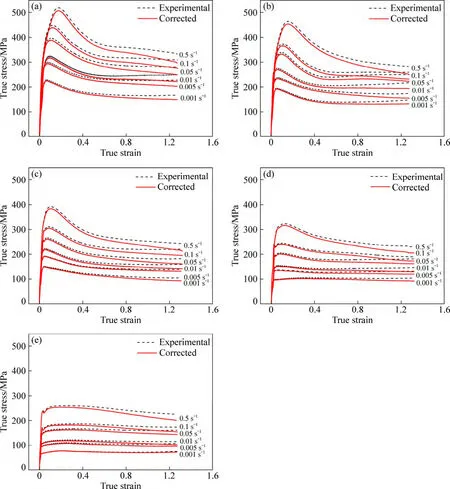
图3 不同变形条件下DP工艺Inconel 718合金摩擦修正前后的真应力-应变曲线Fig. 3 True stress-strain curves of delta-processed Inconel 718 before and after correction under different conditions: (a) 900 ℃; (b) 940 ℃; (c)980 ℃; (d) 1020 ℃; (e) 1060 ℃

式中:l为压缩结束后试样的高度; Δ R=RM-RT;RM为最大鼓肚半径;RT为与压头接触的试样底面半l Δ为压缩结束后试样高度的变化。
采用该摩擦修正方法对热压缩实验获得的真应力-真应变曲线进行摩擦修正,修正后结果绘制成曲线,结果如图3所示。
2.1.2 压缩过程温度影响修正
热变形过程势必产生热量,在形变基体内部来不及散出,可能会造成试样温度升高,即产生所谓的绝热温升效应,这一点在高应变速率下尤为明显。BARAGAR[26]研究指出,绝热温升效应所产生的温度升高(ΔT)为


式中:β为产生热量所占总变形能量的比例,一般认为热变形产生的能量大约85%~90%转变为热量,其余能量则转变为其他形式(例如用于微观结构变化等)。相应地,绝热温升效应引起的试样温度升高会导致相应的流变应力值下降,其下降值Δσ可计算为

式中:Q为变形激活能;n为应力指数;α为材料常数;T为热力学温度;R为摩尔气体常数,8.314 J/(mol·K)。
与Gleeble热压缩实验不同,MTS压缩实验时试样表面没有焊接测温热电偶,无法测量试样变形过程中的温度变化。根据BARAGAR[26]的研究结果,普通钢材以2.0 s-1的应变速率进行热压缩实验时,最大流变应力误差仅为10.3 MPa。吾志岗等[27]的研究结果表明,当镍基高温合金应变速率为1.0 s-1时,试样最大温升为10 ℃左右,这对于变形温度1000 ℃左右的材料来说可以忽略不计。相应地,本实验中的最大应变速率仅为0.5 s-1,在热变形过程中的温度升高和相应的应力误差值均较小,在后续的计算过程中可以忽略,因此,这里不对实验应力应变曲线进行温度修正。
2.2 热变形本构方程
选取经摩擦修正后的真应力-真应变曲线数值,建立DP工艺Inconel 718合金热压缩过程的流变应力本构方程,研究结果[28-29]表明,金属材料的高温变形是一个热激活过程,在高温塑性变形条件下,流变应力主要取决于应变(ε)、变形温度(T)和应变速率(ε˙),通常应用下列式(8)~(10)来表示流变应力的本构模型:
1) 在低应力水平下,


式中:ε˙为应变速率,s-1;A为结构因子,s-1;α为应力水平参数,MPa-1;σ可表示峰值应力或稳态流变应力,或相应于某指定应变量时对应的流变应力,这里表示峰值应力;且满足如下条件:

根据高温压缩实验的结果,基于式(10)建立Inconel 718合金高温变形条件下的本构模型。
ZENER等[30]提出并实验验证了应变速率(ε˙)和变形温度(T)的关系可用Z参数表示,即Zener-Hollomon参数,并结合式(10)可得:
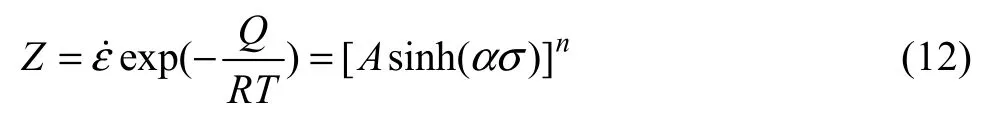
分别对式(8)和(9)两边取对数,可得:
在低应力水平下,
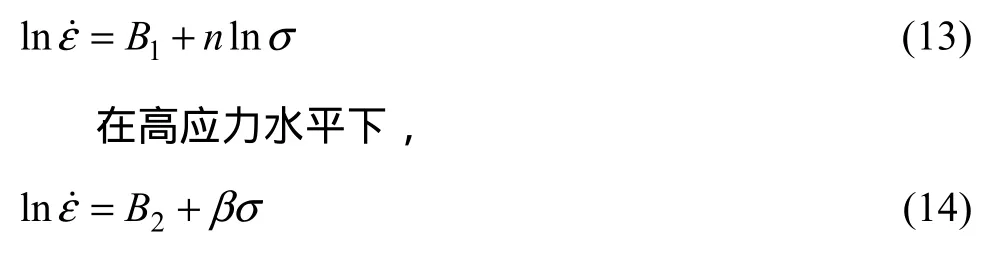
式中:B1和B2为与温度有关的常数。
当温度一定时,β 和n分别为lnε˙-lnσ和lnε˙-σ曲线的斜率。用不同变形温度下峰值应力绘制lnε˙- lnσ 和lnε ˙-σ关系曲线,其结果如图 4(a)和(b)所示,然后对图4中曲线进行一元线性回归处理,则其斜率分别为 n和 β。经循环计算代入可得,在1020~1060 ℃的变形条件下, α σ≤ 0 .8,故取 1020和1060 ℃下n的平均值与900、940和980 ℃下β的平均值,经计算后可得出 n=5.38945,β=0.02376,则α=β/n=0.004408 MPa-1。
对式(10)两边取对数并微分可得

式(1 5)右边的两项分别为一定温度下ln ε ˙-ln[sinh(ασ)]关系曲线的斜率和一定应变速率下ln[sinh(ασ)]-1/T 关系曲线的斜率,分别如图5(a)和(b)所示。将所得的斜率的平均值代入式(15)后可得Inconel 718合金的热变形激活能Q=468.77 kJ/mol,这与WANG等[31]报道的δ相时效态Inconel 718合金激活能467 kJ/mol相近,但高于固溶态Inconel 718合金的激活能,如WEIS等[15]报道的激活解为423 kJ/mol,YUAN等[11]报道的激活解为443 kJ/mol,WANG等[12]报道的443 kJ/mol,δ相时效态Inconel 718合金激活能的增加可能与预先析出的δ相对热变形机制的影响有关。

图4 应变速率与流变应力关系曲线Fig. 4 Relationship between strain rate and flow stress: (a)lnε˙- lnσ ;(b) lnε˙-σ
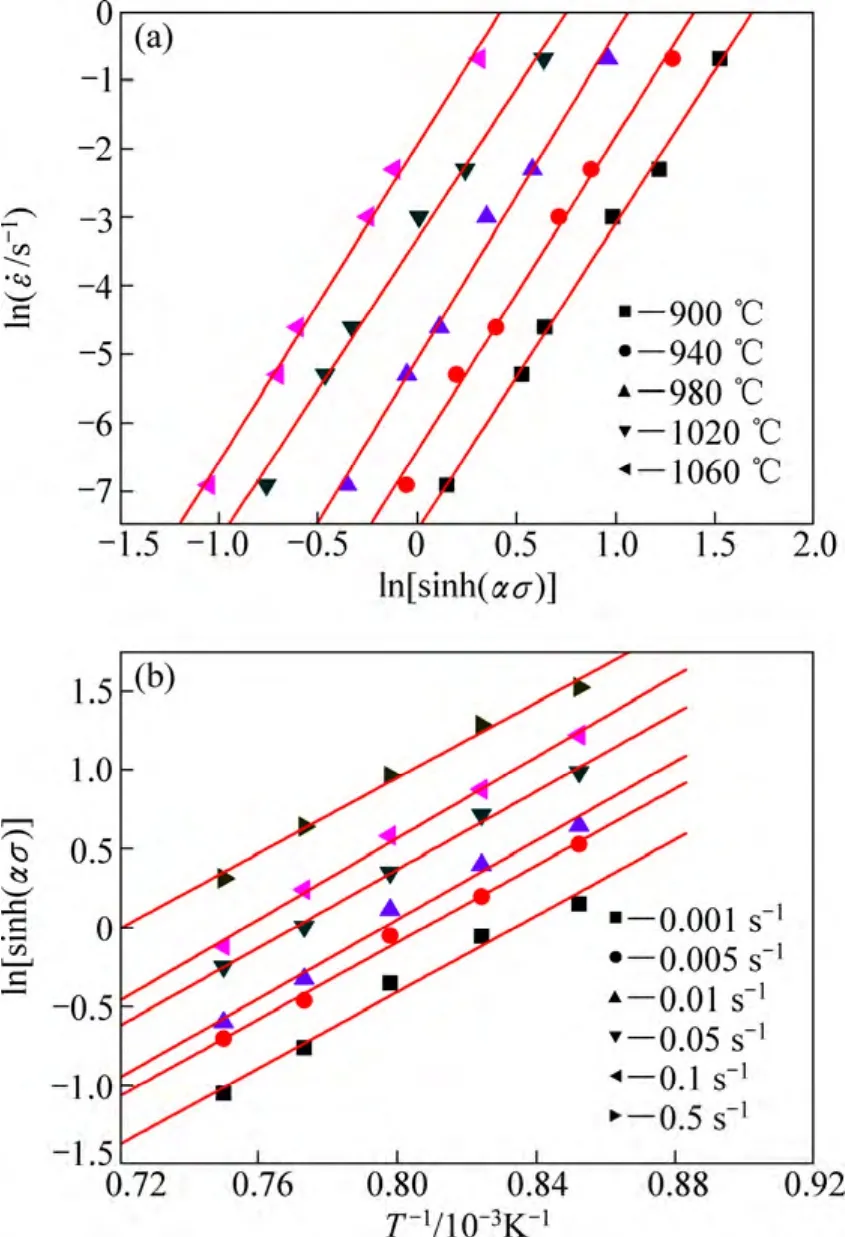
图5 l n ε ˙-ln[sinh(ασ)]曲线和ln[sinh(ασ)]-1/T曲线Fig. 5 Curves of ln ε ˙-ln[sinh(ασ)] (a) and ln[sinh(ασ)]-1/T (b)
将式(12)两边取对数,可得
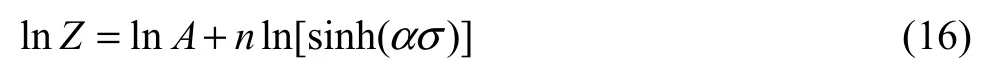
将所求Q值和不同变形温度下的应变速率代入式(12),可得到不同的 Z值,绘制 ln Z -ln[sinh(ασ)]关系曲线,如图6所示,可得n=4.55,A=2.923×1017s-1,α=β/n=0.0052 MPa-1。
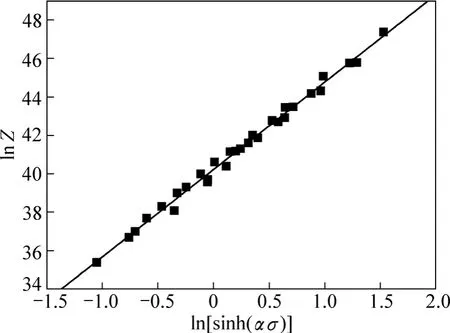
图6 流变应力与Z参数关系Fig. 6 Relationship between flow stress and Zener-Hollomon parameter
将求得的Q、n、A和α等参数代入式(10),获得修正后DP工艺Inconel 718合金的高温变形本构方程:
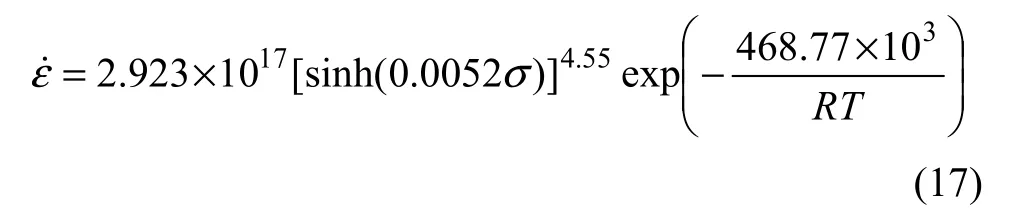
继而,采用上述计算Q、n、lnA和α值的方法可计算出不同应变量下的材料常数,进行非线性拟合回归,获得α、Q、n和lnA值与应变量之间的函数关系式:


式(18)~(21)并综合式(10)构成DP工艺Inconel 718合金高温变形本构模型,利用该模型可用于预测特定真应变时的流变应力值,也可利用式(12)来计算不同应变量条件时的真应力数值:

为了检验所建立引入应变量参数的 DP工艺Inconel 718合金流变应力本构模型的预测精度,将依据模型计算数据和实验获取经修正后的真应力-真应变数据进行了分析比较,如图7所示,引入标准统计参数即相关系数(Rr)和平均相对误差绝对值(E)来对其进行评价:

式中:Ei为实验值;Pi为预测值;和分别为 Ei和Pi的平均值;N为所研究数据点数目。

图 7 修正的应力-应变曲线与预测本构模型计算的应力-应变曲线对比Fig. 7 Comparison between revised stress-strain curves and calculated stress-strain curves by prediction constitutive modeling: (a) 900 ℃; (b)940 ℃; (c) 980 ℃; (d) 1020 ℃; (e) 1060 ℃
利用数据处理软件Origin计算出实验数据值和预测数据值的相关性系数为0.998,平均相对误差绝对值为 3.87%,说明预测值和实验值吻合度较高,所建立的引入应变量的流变应力本构模型能够准确的预测DP工艺Inconel 718合金不同变形量时的实际应力值,如图8所示。
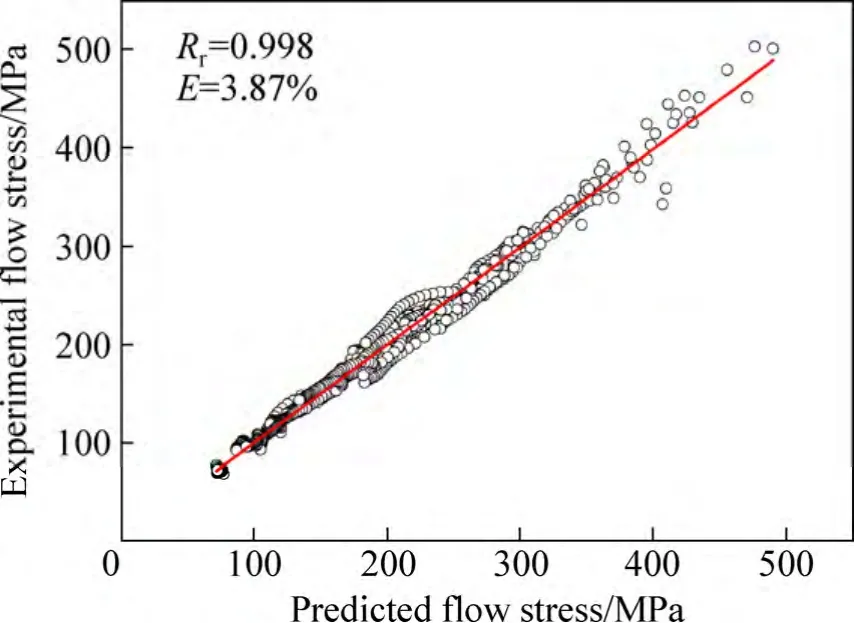
图8 实验数据和预测数值统计Fig. 8 Correlations between experimental and predicted flow stress
3 结论
1) 分析了经DP工艺处理的Inconel 718合金高温热压缩过程中的摩擦因数和绝热温升效应的影响,并对摩擦引起的流变应力差异进行了修正,随着应变速率的增大和变形温度的降低,摩擦因数的影响趋于明显。
2) 经DP工艺处理的Inconel 718合金变形激活能(Q) 和材料常数 (如n、α和A)与其应变量有关,本研究中实验条件下变形激活能数值变化范围为 395~463 kJ/mol。
3) 引入应变量建立了用于预测 DP工艺处理的Inconel 718合金不同变形量时的流变应力本构模型,误差分析表明,实验值与预测值的相关性系数为0.998,平均相对误差绝对值为3.87%,能够准确预测不同变形量时的流变应力值。
[1] KENNEDY R L. Allvac® 718TM, superalloy for the next forty years[C]//LORIA E A. Sixth International Symposium on Superalloys 718, 625, 706 and Derivatives. Pennsylvania: TMS,2005: 1-14.
[2] 郭建亭. 高温合金材料学[M]. 北京: 科学出版社, 2010.GUO Jian-tin. Materials science and engineering for superalloys[M]. Beijing: Science Press, 2010.
[3] 罗恒军, 谢 静, 程 槿. GH4169合金涡轮盘锻件晶粒度分析和控制[J]. 大型铸锻件, 2010, 6: 17-19.LUO Heng-jun, XIE Jing, CHENG Jin. Analysis and control of grain size of GH4169 alloy turbine disc forging[J]. Heavy Casting and Forging, 2010, 6: 17-19.
[4] 庄景云. 变形高温合金 GH4169锻造工艺[M]. 北京: 冶金工业出版社, 2008.ZHUANG Jin-yun. Forging process of wrought super alloy GH4169[M]. Beijing: Metallurgical Industry Press, 2008.
[5] RUIZ C, OBABUEKI A, GILLESPIE K. Evaluation of the microstructure and mechanical properties of delta processed alloy 718[C]//ANTOLOVICH S D. Seventh International Symposium on Superalloys. Pennsylvania: TMS, 1992: 33-42.
[6] DIX A W, HYZAK J M, SINGH R P. Application of ultra fine grain alloy 718 forging billet[C]//ANTOLOVICH S D.Superalloys. Warrendale, PA: TMS, 1992: 23-32.
[7] BHOWAL P R, SCHIRRA J J. Full scale Gatorizing TM of fine grain Inconel718[C]//LORIA E A. Superalloys 718, 625, 706 and various derivatives. Warrendale, PA: TMS, 2001: 193-201.
[8] 吕宏军, 姚草根, 张凯峰, 贾新朝. GH4169合金细晶成形工艺与机理及其性能研究[J]. 机械工程材料, 2003, 27(1): 15-18.LÜ Hong-jun, YAO Cao-gen, ZHANG Kai-feng, JIA Xin-chao.Fine-grain forming process, mechanism and properties of GH4169 alloy[J]. Materials for Mechanical Engineering, 2003,27(1): 15-18.
[9] 张海燕, 张世宏, 程 明. Delta工艺中Inconel 718合金中δ相的演变机制[J]. 金属学报, 2009, 45(12): 1451-1455.ZHANG Hai-yan, ZHANG Shi-hong, CHENG Ming. Evolution of δ phase in Inconel 718 alloy during delta process[J]. Acta Metallurgica Sinica, 2009, 45(12): 1451-1455.
[10] ZHANG H Y, ZHANG S H, CHENG M. Deformation characteristics of δ phase in the delta-processed Inconel 718 alloy[J]. Materials Characterization, 2010, 61: 49-53.
[11] YUAN H, LIU W C. Effect of the delta phase on the hot deformation behavior of Inconel 718[J]. Mater Sci Eng A, 2005,408: 281-289.
[12] WANG Y, ZHEN L, SHAO W Z, YANG L, ZHANG X M. Hot working characteristics and dynamic recrystallization of delta-processed superalloy 718[J]. J Alloy Compd, 2009, 44:341-346.
[13] 王 岩, 邵文柱, 甄 良. GH4169合金δ相的溶解行为及对变形机制的影响[J].中国有色金属学报, 2011, 21(2): 341-349.WANG Yan, SHAO Wen-zhu, ZHEN Liang. Dissolution behavior of δ phase and its effects on deformation mechanism of GH4169 alloy[J]. The Chinese Journal of Nonferrous Metals,2011, 21(2): 341-349.
[14] CONE F P. Observations on the development of delta phase in Inconel 718 alloy[C]//LORIA E A. Superalloys 718, 625, 706 and various derivatives. Warrendale, PA: TMS, 2001: 323-332.
[15] WEIS M J, MATAYA M C, THOMPSON S W. The hot deformation behavior of an as-cast alloy 718 ingot[C]//LORIA E A. Superalloys 718. TMS, Warrendale, PA, 1989: 135-154.
[16] ZHOU L X, BAKER T N. Effects of strain rate and temperature on deformation behaviour of IN 718 during high temperature deformation[J]. Mater Sci Eng A, 1994, 177: 1-9.
[17] ZHANG J M, GAO Z Y, ZHUANG J Y, ZHONG Z Y.Mathematical modeling of the hot-deformation behavior of superalloy IN718[J]. Metallurgical and Materials Transactions A,1999, 30: 2701-2713.
[18] GUEST R P, TIN S. The dynamic and metadynamic recrystallization of IN718[C]//LORIA E A. Superalloys 718, 625,706 and Various Derivatives, Warrendale, PA: TMS, 2005:373-383.
[19] THOMAS A, EL-WAHABI M, CABRERA J M, PRADO J M.High temperature deformation of Inconel 718[J]. J Mater Process Technol, 2006, 177: 469-472.
[20] 杨 平, 赵玉涛, 王安东, 缪 栋, 陈 刚, 何 毅. Delta 工艺Inconel 718合金热变形条件下的流变行为[J]. 中国有色金属学报, 2012, 22(1): 72-79.YANG Pin, ZHAO Yu-tao, WANG An-dong, MIAO Dong,CHEN Gang, HE Yi. Flow stress behavior of delta-processed Inconel 718 superalloy under hot compression deformation[J].The Chinese JournaI of Nonferrous Metals, 2012, 22(1): 72-79.
[21] 严 巍, 陈国学. 轴对称压缩流动应力-应变曲线有限元修正方法的研究[J]. 塑性工程学报, 2004, 11(4): 19-21.YAN Wei, CHEN Guo-xue. Study on the correction of the material flow stress-strain curves in axisymmetric compression test[J]. Journal of Plasticity Engineering, 2004, 11(4): 19-21.
[22] TSENG A A, HORSKY J, RAUDENSKY M, KOTRBACEK P.Deformation behavior of steels in mushy state[J]. Mater Design,2001, 22(2): 83-92.
[23] 许树勤, 陈志英, 张善元. 镦粗试验中鼓度与摩擦的相关性研究[J]. 锻压技术, 2004, 29(5): 46-48.XU Shu-qin, CHEN Zhi-ying, ZHANG Shan-yuan. Research on the relation between bulging and friction in cylinder upsetting[J].Forging & Stamping Technology, 2004, 29(5): 46-48.
[24] 汪大年. 金属塑性成形原理[M]. 北京: 机械工业出版社,1982: 140.WANG Da-nian. Principles of metal forming[M]. Beijing: China Machine Press, 1982: 140.
[25] EBRAHIMI R, NAJAFIZADEH A. A new method for evaluation of friction in bulk metal forming[J]. J Mater Process Technol, 2004, 152(20): 136-143.
[26] BARAGAR D L. The high temperature and high strain-rate behavior of a plain carbon and an HSLA steel[J]. Journal of Mechanical Working Technology, 1987(14): 295-307.
[27] 吾至岗, 李德富. GH625镍基合金的高温压缩变形行为及组织演变[J]. 中国有色金属学报, 2010, 20(7): 1321-1327.WU Zhi-gang, LI De-fu. Hot compression deformation behaviors and microstructure evolution of GH625 Ni-based alloy[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(7):1321-1327.
[28] LAASRAOUI A, JONAS J J. Prediction of steel flow stresses at high temperatures and strain rates[J]. Metallurgical Transactions A, 1991, 22(7): 1545-1557.
[29] KARHAUSEN K, KOPPER R. Model for integrated process and microstructure simulation in hot forming[J]. Steel Reasearch,1992, 63(6): 247-256.
[30] ZENER C, HOLLOMOM J H. Effect of strain rate upon plastic flow of steel[J]. Journal of Applied Physics, 1994, 15(1): 22-26.
[31] WANG Y, SHAO W Z, ZHEN L, ZHANG B Y. Hot deformation behavior of delta-processed superalloy 718[J]. Mater Sci and Eng A, 2011, 528: 3218-3227.

