玻璃纤维中总铁含量测定的不确定度评定

张亮亮,郑兆和

(广州纤维产品检测研究院,国家纺织品服装服饰产品质量监督检验中心,广东广州510000)

玻璃纤维中总铁含量测定的不确定度评定

张亮亮,郑兆和

(广州纤维产品检测研究院,国家纺织品服装服饰产品质量监督检验中心,广东广州510000)

采用火焰原子吸收分光光度计对玻璃纤维中的总铁含量进行测定,分析了测定过程中各个分量引入的不确定度以及对合成不确定度的影响。采用代入法解决了校准曲线的非线性回归拟合引入的不确定度难以计算的问题,得出该测定方法的扩展不确定度为(0.11±0.01)%,k=2。

玻璃纤维;总铁含量;不确定度

测量不确定度表示被测量值的分散性,是评定测量结果质量高低的一个重要指标,正确评定不确定度成为测量过程的重要一环。在仪器分析中,校准曲线的回归拟合引入的不确定度分量往往是合成不确定度的一个主要分量。由于测量元素含量范围较大,根据朗伯比尔定律,其校准曲线往往是非线性的,如何评定非线性回归拟合引入的不确定度鲜见报道[1],本文采用替代法解决了非线性回归拟合引入的不确定度计算困难的问题。采用火焰原子吸收分光光度计对玻璃纤维中的总铁含量进行测定,分析了测定过程中不确定度的来源、大小以及对合成不确定度的影响。从计算结果看,校准曲线的非线性回归拟合引入的不确定度、重复性及消解的回收率对合成不确定度的影响是主要的,其他分量可忽略不计。

1 实验部分

1.1 测试原理

玻璃纤维样品用高氯酸和氢氟酸进行湿法消解后,在盐酸酸性溶液中,利用原子吸收分光光度计(FAAS)对消解后的溶液进行测试,根据测试浓度计算玻璃纤维中总铁含量。

1.2 仪器和试剂

仪器:耶拿Contr AA700型AAS,AB204-S型电子天平(梅特勒托利多仪器上海有限公司)。

试剂:1 000μg/m L铁元素标准储备液(国家金属制品及电子材料分析测试中心)。

1.3 测试方法

称取约0.1 g的玻璃纤维样品,精确到0.000 1 g,放入聚四氟乙烯坩埚中,加入2 ml高氯酸和5 ml氢氟酸,升温至高氯酸白烟冒尽,冷却后加入4 ml盐酸和10 ml水,加热至盐类全部溶解,冷却后过滤溶液至容量瓶中,加去离子水定容至100 ml。同时按照上述步骤处理一个空白(酸液)。测试流程如图1所示。

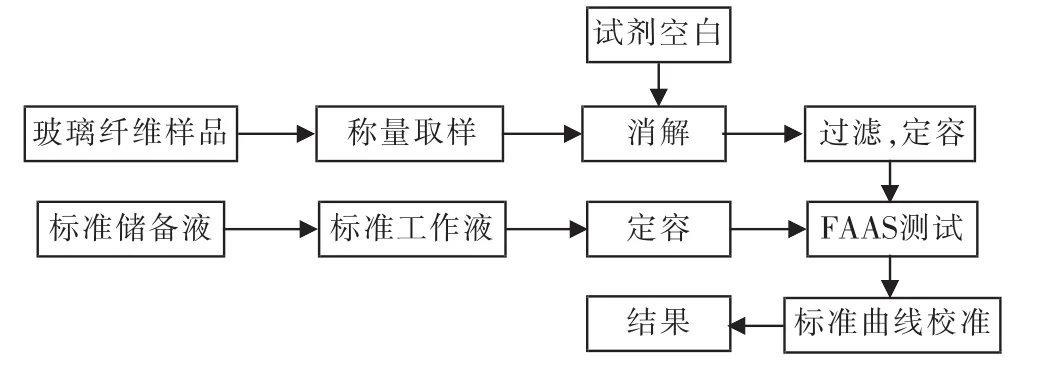
图1 样品测试流程图

1.4 数学模型

计算玻璃纤维中总铁(以Fe2O3计)的含量w:

式中 ci——试样溶液中Fe2O3质量浓度(mg/L);c0——空白溶液中Fe2O3质量浓度(mg/L); V——定容体积(ml);m——试样质量(g)。

1.5 不确定度来源

产生不确定度的因素通常包括检测仪器、实验环境、标准物质、前处理方法、人员操作和分析方法。影响测量不确定度的来源有两类。

1.5.1 A类不确定度

(1)测试重复性的标准偏差(包括天平称量重复性、体积重复性、试样均匀性和代表性等)。

(2)标准曲线拟合时产生的不确定度。

(3)样品消解过程回收率R:样品消解回收率引入的不确定度。

1.5.2 B类不确定度

(1)试样的质量m:包括天平误差和分辨率引入的不确定度。

(2)测定试样的溶液浓度Ci:包括标准物质引入的不确定度、标准溶液配制引入的不确定度等。

(3)待测溶液的定容体积V:包括容量瓶校准时引入的不确定度及温度变化引入的不确定度。

2 结果与讨论

平行测试11份样液,得到样品溶液中总铁有检出,评定其测量的不确定度。

2.1 测量重复性引入的不确定度

在整个处理过程中,因消解引入的不确定度有温度、时间、加入试剂的量、消解/反应/效率、容器附着量、容量瓶定容时人眼观察凹液面与刻线是否持平等引入的不确定度分量,可通过平行测定样品来评估不确定度分量。

在重复性条件下,对该样品进行11次独立测试,得出玻璃纤维样品中Fe2O3含量分别为0.116%、0.122%、0.119%、0.105%、0.110%、0.115%、0.109%、0.108%、0.116%、0.109%和0.109%,则Fe2O3测试结果的算术平均值:

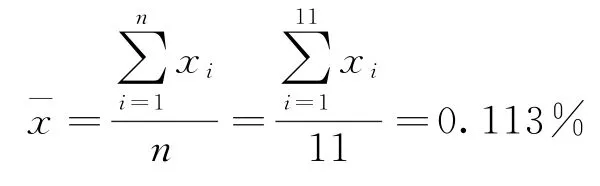
重复测定的标准偏差:

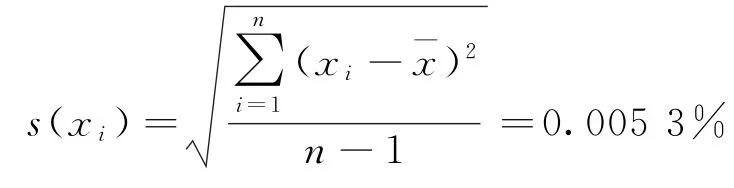
重复测定的标准不确定度:

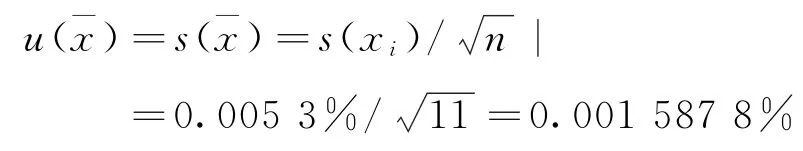
重复测定的相对标准不确定度:

2.2 称量过程引入的标准不确定度u(m)

称量过程的不确定度主要来自天平的准确性、天平的分辨率和称量过程的重复性,其中称量过程的重复性引入的不确定度分量已包含在各种因素造成的重复性影响修正值不确定度分量中。

2.2.1 天平准确性引入的标准不确定度分量u1(m)

按照检测标准要求,使用的天平最小精度为0.1 mg,实验室所用电子分析天平经计量校准合格,天平在0≤m≤50 g时,MPE=0.5 mg,按均匀分布换成标准不确定度为:

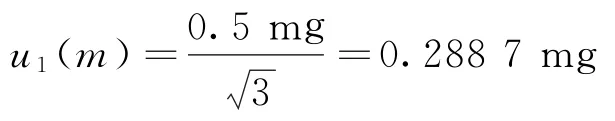
2.2.2 电子天平分辨率引入的标准不确定度分量u2(m)

电子天平的分辨率为0.1 mg,按照均匀分布,则

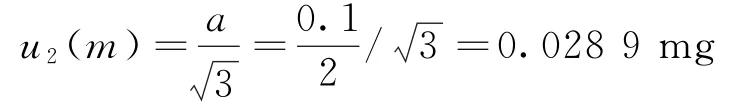
称量过程引入的标准不确定度u(m)为:

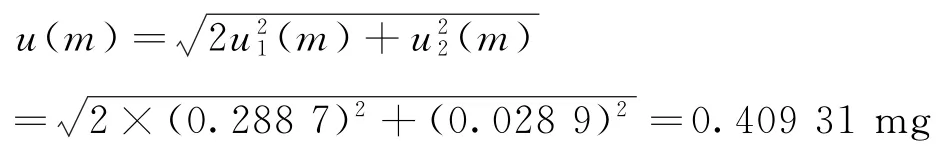
则相对标准不确定度为:

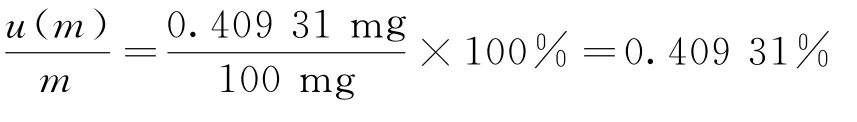
2.3 测定浓度C的不确定度u(c)

测定浓度C的不确定度由两部分构成,首先是7个浓度标准溶液的浓度和吸收强度Abs值拟合的曲线求得浓度为C时测量所产生的不确定度;其次是由标准储备液配制成标准溶液时所产生的对测定浓度C测量带来的不确定度。

2.3.1 标准曲线拟合时引入的不确定度u1(c)

实验采用7个浓度水平点的Fe标准溶液,用FAAS法测定其吸收强度,每一浓度点测定3次,数据如表1所示,得到以下曲线方程:

Y=(a+bx)/(1+cx),R2=0.999 65

其中 a=0.002 003 1,b=0.166 333 1,c=0.096 015 7

Y=(b-ac)z+a,斜率B1=b-ac=0.166 14

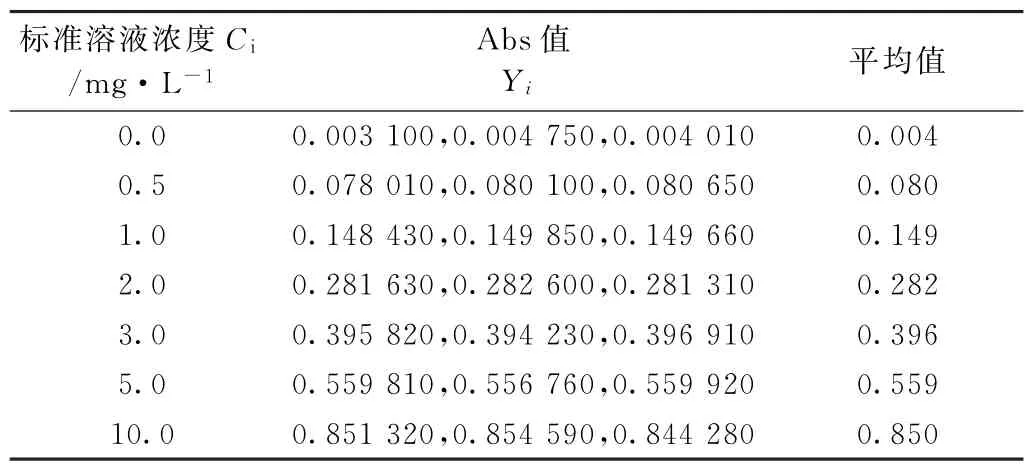
表1 Fe标准溶液浓度与吸收强度的标准曲线

实验对样品测定液进行了11次测定,由曲线方程求得各次测量的值后计算其平均质量浓度为C0= 0.802 3 mg/L,通过简化后一元线性方程Y=(bac)z+a,得到浓度C的标准不确定度为:

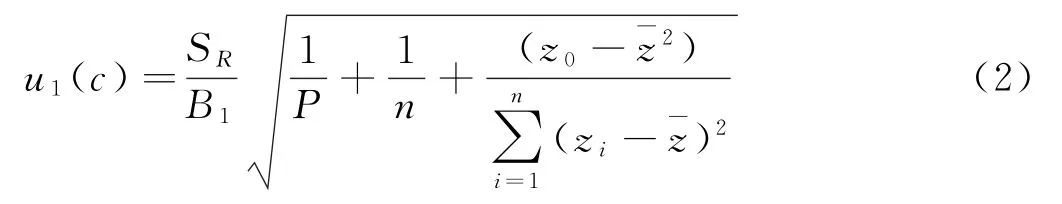
式中 B1——简化后工作曲线的斜率(B1=0.166 14);P——样品C0的测定次数(P=11);n——配制7个标准溶液浓度点,每个浓度点测定3次,共计21次,即n=21;SR——工作曲线的标准偏差;¯z——标准溶液的质量浓度平均值代入得到(mg/L);z0——实验样品测得值C0代入得到(mg/L)。则有:

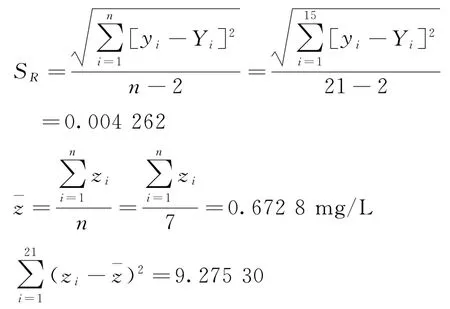
将上述各值代入式(2)中得出

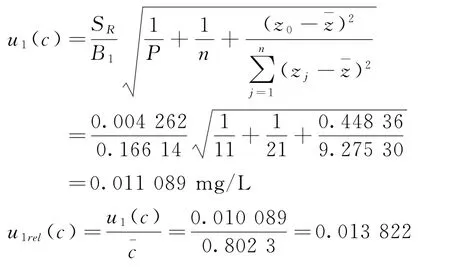
2.3.2 标准溶液配制引入的不确定度

(1)标准储备液引入的不确定度

1 000μg/m L的Fe标准储备液的扩展不确定度为0.7%,则相对标准不确定度为:

urel(CFe)=0.7%÷2=0.003 5

(2)标准储备液稀释过程引入的不确定度

用1 ml分度吸量管吸取1 ml Fe标准储备液,置于100 ml容量瓶(A级)中,用1%硝酸溶液定容至刻度制成10 mg/L标准使用液。吸量管导致的不确定度:JJG196-2006《常用玻璃量器》规定1 ml分度吸量管吸取1 ml时容量最大允许误差为±1.5%,按矩形分布,则:

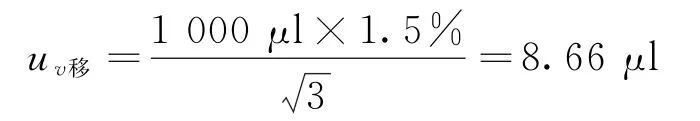
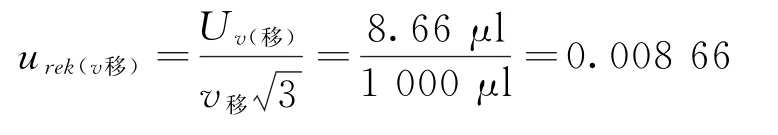
(3)容量瓶体积引入的不确定度

JJG196-2006《常用玻璃量器》规定,20℃时,100 ml容量瓶(A级)的容量最大允许误差为0.1 ml,属于均匀分布,包含因子,则容量瓶带来的标准不确定度:

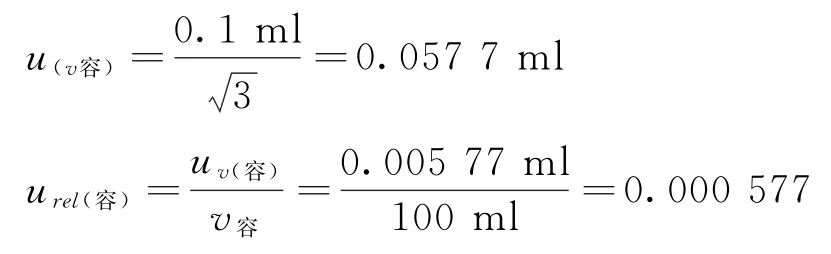
(4)标准溶液逐级稀释引入的不确定度

以10 mg/L的重金属标准溶液再稀释配成0.5、1.0、2.0、3.0、5.0和10 mg/L的标准工作液,由于标准曲线拟合时已考虑X轴上标准溶液逐级稀释引入的不确定度远小于Y轴上引入的不确定度,因此标准溶液逐级稀释引入的不确定度可以忽略不计[2]。

标准溶液配制引入不确定度分量合成得到体积的标准不确定度为:

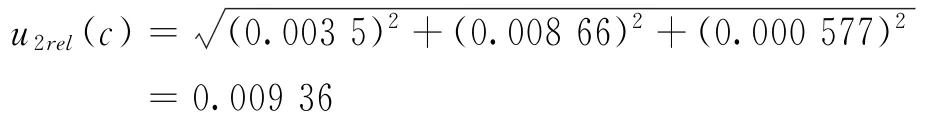
则测定溶液浓度C引入的相对标准不确定度为:

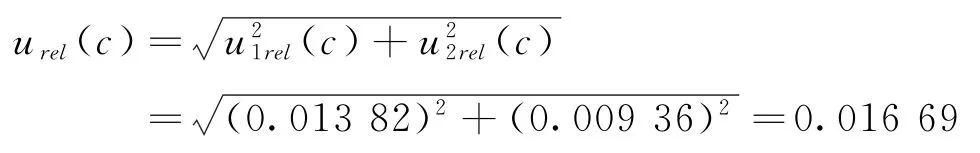
2.4 待测溶液容量体积V引入的不确定度

20℃时100 ml容量瓶(A级)的容量允差为±0.1 ml,属于均匀分布,包含因子,则容量瓶带来的标准不确定度为:

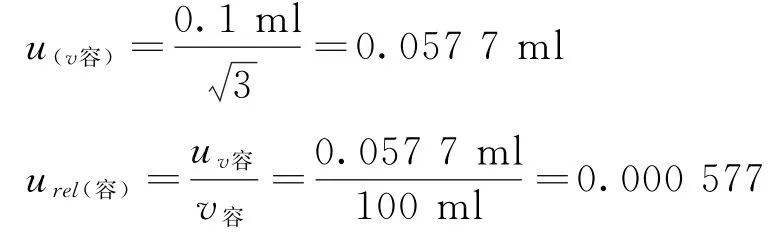
由于本实验是在接近20℃度的条件下进行的,故温度对体积的影响可以忽略不计。

2.5 样品消解回收率引入的不确定度

由于样品消解不完全或消解过程导致重金属的损失或污染及消解液转移过程的损失等,将使样品中的重金属质量分数不能100%进入到测定液中,由于本标准没有对回收率进行规定,根据JJF 1059.1-2012《测量不确定度评定与表示》,本方法将按实际回收率计算不确定度[3]。

在重复性条件下,按照本方法采用与实际样品总铁含量接近的1.0 mg/L标准溶液进行加标回收率测试,进行了9次独立测试,Fe2O3的回收率分别是为111.28%、106.41%、116.32%、107.50%、115.15%、100.65%、111.28%、109.93%和102.81%,则Fe2O3回收率测试结果的算术平均值为:

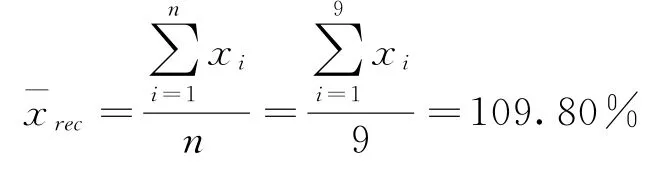
回收率测定的标准偏差:

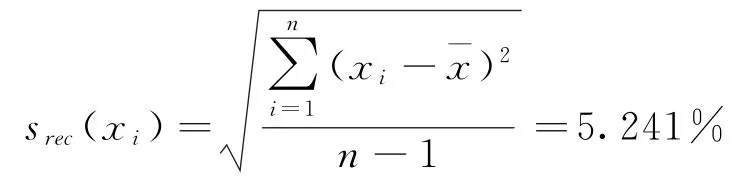
回收率测定的标准不确定度:

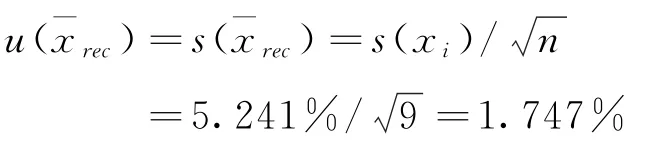
回收率测定的相对标准不确定度:

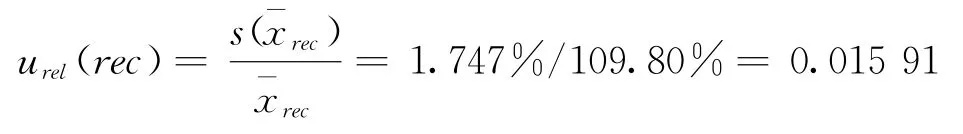
2.6 合成标准不确定度

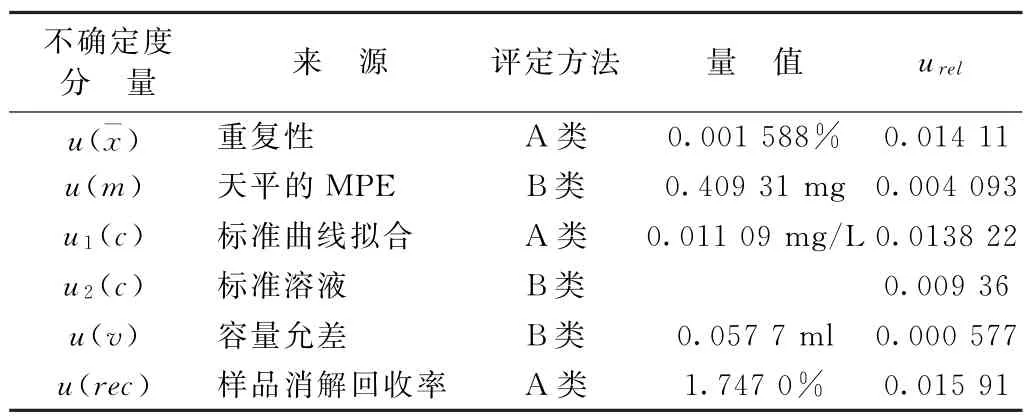
表2 不确定度分量

将各不确定度分量列于上表中,由上述各相对标准不确定度合成玻璃纤维中总铁含量测定结果的相对标准不确定度为:

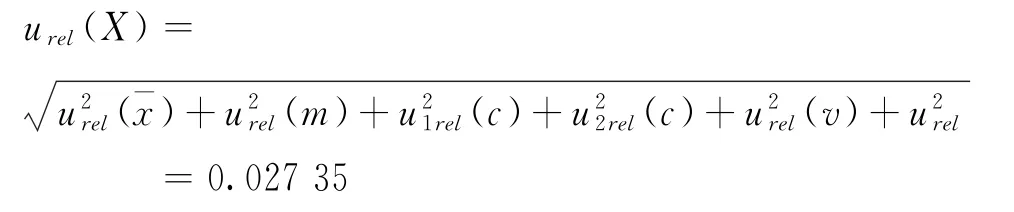
合成标准不确定度为:

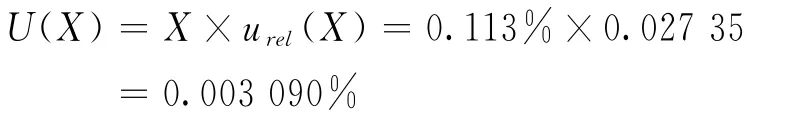
2.7 扩展不确定度

取包含因子k=2,则扩展不确定度为:

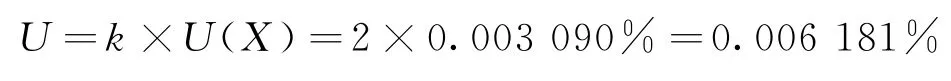
3 结论

玻璃纤维中总铁含量(以Fe2O3计)测定结果为: X(Fe2O3)=(0.11±0.01)%,k=2。

(1)采用原子吸收光谱法测定玻璃纤维中的总铁含量时,影响测量不确定度的主要来源有重复性、标准曲线拟合及样品消化回收率。

(2)代入法是校准曲线非线性回归拟合引入不确定度计算困难的有效解决方案。

(3)标准溶液的配制、试样质量m及定容体积V对不确定度的影响可忽略不计。

[1]占永革,黄湘燕,龚 剑.化学分析中非线性曲线拟合结果的不确定度评定[J].冶金分析,2011,31(8):26-30.

[2]林 媚,平新亮,姚周麟,等.茶叶中铜含量测定的不确定度分析[J].计量与测试技术,2010,37(8):63-64.

[3]JJF 1059.1-2012,测量不确定度评定与表示[S].

Uncertainty Evaluation for the Determination of Total Iron Content in Glass Fiber

ZHANG Liang-liang,ZHENG Zhao-he
(Guangzhou Fiber Product Testing and Research Institute,National Quality Supervision and Inspection Center of Textile Garment and Accessories(GZ),Guangzhou 510000,China)

Based on the measurement of iron content in glass fiber by FAAS,the sources of the uncertainty of measurement were analyzed.In order to evaluate the uncertainty of non-linear curve fitting results,the non-linear curve was transformed into linear curve by substitution method.The expanded uncertainty of the measured results was(0.11±0.01)%,k=2.

glass fiber;total iron content;uncertainty

TS101.92

:A

:1673-0356(2015)03-0063-04

2015-03-03

张亮亮(1987-),男,助理工程师,主要从事纺织品检测工作。