红外目标模拟器CIG系统延时误差分析及补偿

王 斐，梁晓庚，王艳奎

(1.河南科技大学信息工程学院，河南洛阳471003;2.中国空空导弹研究院，河南洛阳471009)

1 引言

在红外成像制导武器研制过程中，半实物仿真系统是极其重要的系统设计和性能评估验证手段，仿真系统的性能和精度是仿真总体最关心的问题［1］。在仿真试验过程中，影响仿真精度的误差因素有许多方面，各仿真分系统的误差对仿真精度的影响不尽相同，理论分析和工程经验均表明，红外目标模拟器分系统的目标红外特性模拟误差对整个半实物仿真系统的仿真精度产生重大影响，进而影响仿真结果的置信度［2－3］。因此深入研究红外目标模拟器的误差因素，找出影响仿真结果的误差源，分析各误差源对仿真结果的影响程度，并采取相应措施设法消除或减小误差，这对提高半实物仿真系统的仿真精度具有重要意义。

本文针对红外目标特性模拟的精度要求，分析了红外目标模拟的主要误差因素，并分析了红外CIG系统延时误差对仿真结果的影响，给出了红外CIG系统延时误差补偿算法，通过仿真试验验证了误差补偿算法。

2 误差影响因素分析

某红外目标模拟器主要由红外计算机图像生成系统(Infrared Computer Image Generator，IR CIG)和红外图像转换与显示系统(Infrared Scene Projector and Display System，IR SPDS)两部分组成，其中IR SPDS又包括红外目标/背景图像发生器和光学投影系统。IR CIG用于处理反馈信息，并产生图像数据;IR SPDS用于将图像数据转换为红外图像，并将红外图像投射至无穷远，作为所需的目标场景。由目标模拟器构成可知，其主要误差来自IR CIG系统、红外目标/背景图像发生器、光学投影系统三部分。

CIG 系统如图1所示［3］。

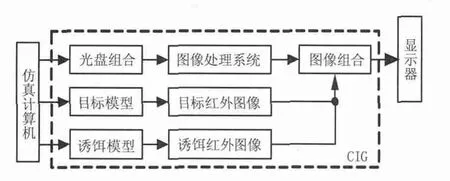
图1 CIG系统Fig.1 CIG system

CIG系统误差主要包括CIG延时误差和像质误差。

由图1可知，仿真计算机产生目标和干扰驱动数据后，需要经过CIG系统若干处理才能形成目标和干扰场景，尽管该过程已经做到尽量实时处理，但从仿真计算机形成指令到CIG系统形成显示场景仍需要若干时间，该过程所经历的时间即为CIG延时，CIG延时包括如下两部分:

(1)CIG计算延时

CIG内部几何处理器和像素处理器以流水方式高速运行，完成图形、光线、颜色、消隐以及大气效应等动态图像生成工作，该运算工作逐帧进行，故CIG系统从缓冲器中提取数据，经过几何处理器和像素处理器的串行处理，造成约一帧延时，该数据帧长约25 ms，故CIG计算延时约为25 ms，该延时必须补偿，否则将极大地影响仿真精度。

(2)仿真机与CIG系统不同步延时

由于仿真机以计算帧频通过I/O通道向CIG缓冲器传送驱动数据，而CIG则在导引头同步信号的控制下，以50 Hz的速率从缓冲器中取得数据，仿真机和CIG之间信号交换不同步，造成二者之间的不同步延时，某CIG系统不同步延时约为15 ms。

上述延时累计约为40 ms，该延时误差必须考虑补偿。

像质误差包括模型误差、标度误差、层次误差、灰度误差、边缘对比度误差等，这些误差对以视线角信息进行制导的制导控制系统仿真可以暂不考虑。

红外目标/背景图像发生器在将CIG输出的带有红外特征的视频场景信息转换为红外图像过程中存在梯形误差、余辉误差、均匀性误差等，只要经过严格测试和校准，保证图像质量，则这些误差对红外成像制导仿真系统的影响暂时可以不予考虑。

光学投影系统将红外图像投射至无穷远，作为所需的目标场景，其误差主要来源于红外目标/背景图像发生器和光学投影系统之间的连接接口，由于安装加工过程中二者的光轴无法做到完全重合，则投影系统投射给导引头的图像必然存在一个固定偏移，该部分误差对制导控制系统仿真精度会造成一定影响，该误差属于系统误差，在使用投影系统前，可以标定好，则这些误差对红外成像制导仿真系统的影响暂时可以不予考虑。

本文将针对红外目标模拟器的红外CIG系统延时误差进行建模，并分析误差补偿方法。

3 红外CIG系统延时误差对仿真结果影响分析

由红外CIG系统误差源分析可知，红外CIG系统存在约40 ms延时，该延时对仿真结果的影响可以从几何分辨率、角度分辨率、延时对动目标横向位置的影响、延时对动目标径向位置的影响四方面分析［4］。

(1)几何分辨率

几何分辨率ΔL含义为每个CIG像素所代表的几何尺寸，计算如下:

式中，ΔL为几何分辨率，单位为米;R为识别距离，单位为米;θ为视场角，单位为度;Npix为二维图像某方向的分辨率。由于视场角通常很小，则式(1)可表示如下:

假定CIG场景的视场大小为3°，分辨率为256×256，导引头在10 km处识别目标，则每个像素此时的几何分辨率ΔL为2.045 m。

(2)角度分辨率

(3)延时对动目标横向位置影响

假定导弹弹体质心为B，目标质心为T，弹目相对运动示意如图2所示。

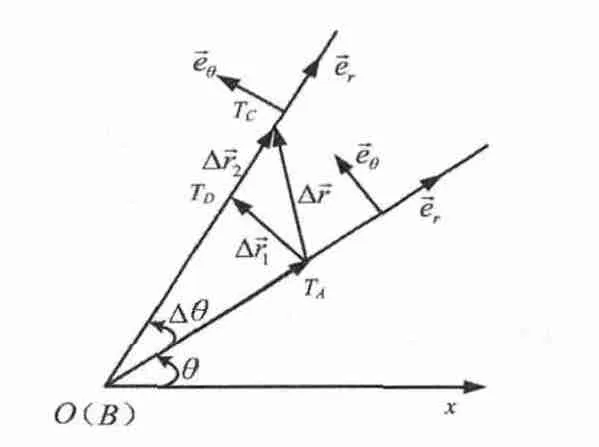
图2 弹目相对运动示意Fig.2 Schematic diagram of relative motion in missile and target

假定目标某时刻在TA处，Δt时间后在TC处，以弹体质心为坐标原点，以为径向单位矢量，以为横向单位矢量，则弹目相对位移为Δ=Δ+Δ，其中Δ为横向位移，Δ为径向位移。若Δt很小，则Δ≈rΔ，Δ≈Δr，图2中为弹目径向速度，为弹目横向速度，和在视线坐标系Ox4y4z4中定义。视线坐标系Ox4y4z4定义如下:原点O取在导弹质心，Ox4轴与弹目视线重合，由导弹指向目标为正;Oy4轴位于包含Ox4轴的纵向平面内，与Ox4轴垂直，指向上方为正;Oz4轴方向按照右手定则确定，位于侧向平面内。

假定导弹和目标运动在惯性水平面XOZ内，若CIG系统延时为τ，目标最大横向速度为VTθ，则系统延时所造成的目标最大横向位置滞后偏差为:

分析可知，CIG系统延时为40 ms，若目标最大横向速度为20 m/s，则系统延时所造成的目标最大横向位置滞后偏差为0.8 m。

(4)延时对动目标径向位置的影响

若导弹运动速度为VB，目标最大径向速度为VTr，则CIG系统延时所造成的目标最大径向位置偏差为:

若导弹最大运动速度为320 m/s，目标最大径向速度为20 m/s，则系统延时40 ms所造成的目标最大径向位置偏差为13.6 m。

径向位置偏差将导致导引头识别到的目标外轮廓尺寸产生偏差，若目标横向宽度为W，则CIG系统所产生的动态视频图像在X方向识别距离为X处，与目标外轮廓尺寸变化所对应的导引头视场角变化为:

式中，W为目标横向宽度，单位为米;Δθ为导引头视场角变化量，单位为弧度。由于视场角通常很小，远距离处目标横向宽度与识别距离相比要小的多，则式(6)可表示为:

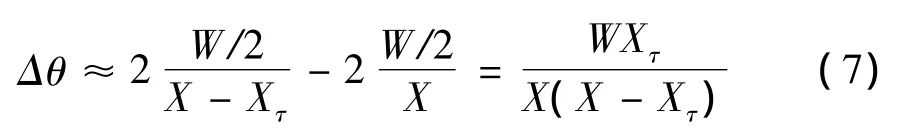
若假定目标横向宽度最大为50 m，则Δθ为0.00041'。

理论分析表明，CIG系统延时导致导引头识别到的目标外轮廓尺寸的角度偏差远远小于该CIG系统的角度分辨率，故延时对动目标横向外轮廓的影响可以不予考虑。

为了考察红外CIG系统延时误差对仿真弹道影响，将标准弹道计算得到的目标位置延时40 ms后，再将目标运动参数送给飞控系统，经测试验证，此时标准弹道条件下考虑延时因素后，其侧偏为3.5 m，不但比标准弹道下侧偏增大，而且还超出每个像素此时代表的几何尺寸。测试验证表明，CIG系统延时误差不能忽略，应该补偿。

4 红外CIG系统延时误差补偿

由于CIG系统缓存和动态视频图像生成过程均存在延时，导致整个CIG系统约延时40 ms，则仿真机下发当前帧目标运动驱动数据给目标模拟器后，目标模拟器产生与该当前帧目标运动驱动数据对应的动态视频图像也必然始终存在约40 ms延时，该延时对仿真精度影响较大，可考虑采用预测外推法基于当前帧数据预测40 ms后的目标运动参数，目标模拟器基于预测数据产生动态视频图像，则此时可使导引头敏感到的目标运动参数与仿真机实时产生的目标运动参数相吻合［5－6］。

尽管实时仿真过程中目标运动存在随机噪声和随机机动，但对某条特定弹道仿真试验而言，目标运动轨迹通常是确定的，故可以考虑根据目标运动方程事先离线生成驱动数据，在目标模拟器实时生成动态视频图像时，以该离线生成驱动数据为目标模拟器每一帧驱动指令的“测量值”，以根据仿真机下发的目标运动驱动数据外推预测40 ms后的目标运动数据为“估计值”，显然，该“估计值”和“测量值”时间上同步，已经补偿了CIG延时。

为了补偿CIG延时，确保目标运动参数预估的实时性并提高数据预估的精度是延时补偿算法的核心。由于随着时间的推移，未来目标运动的扰动因素会不断对系统造成影响，导致新旧数据对预测效果产生不同的影响，故应对新旧数据进行加权，以削弱旧数据作用;另外，考虑到实时性要求，有必要采用在线实时递推预估算法。本文采用渐消记忆递推最小二乘估计算法来对目标运动参数进行在线预估。

构造序列 xn的 AR(p)模型［7］如下:

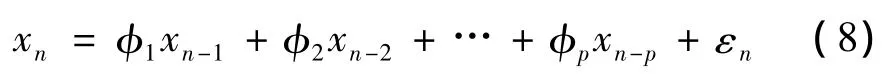
式(8)可以改写如下:

式中:

for k≤0，则xk=0。

其最小二乘解为:

模型残差信号如下:

当AR(p)模型参数随时间变化时，在参数递推过程中，由于采用渐消记忆的最小二乘参数实时递推算法，故对新旧历史数据可以施加不同的权重，降低旧数据影响，提高新数据的可信度，使其有效克服数据饱和现象，获得跟踪参数变化的实时估计［8］，其准则函数为:

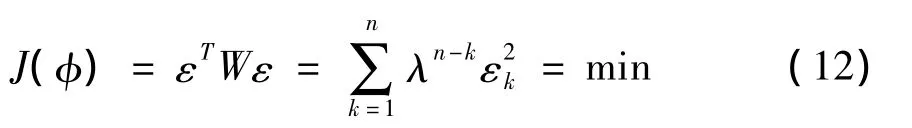
其中:

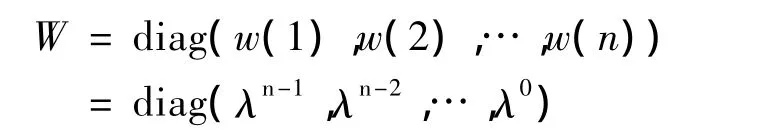
式(12)中λ为渐消记忆因子，0＜λ≤1，一般取λ =0.9 ～ 0.99 ，此处取 λ =0.9 。

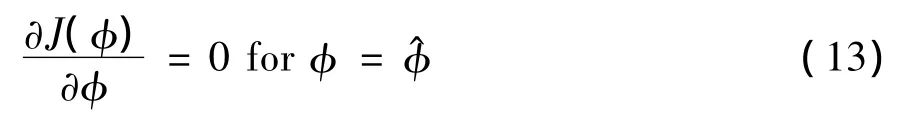
则渐消加权最小二乘估计为:

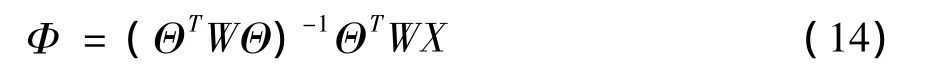
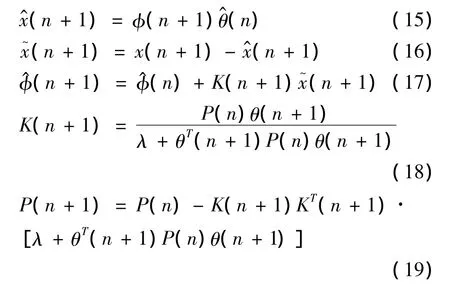
尽管AR(p)模型中阶次p存在最优阶次选择的问题，但对阶次p大于2的系数一般都很小，为了降低数据处理负荷，保证目标运动参数预测的实时性，可选AR(2)模型对经过预处理的数据进行建模外推预测。此时有:

5 仿真结果

为检验补偿算法性能，对该算法进行计算仿真。CIG系统总延时取40 ms，仿真机帧时取2 ms，以仿真机计算下发的目标运动数据作为驱动数据，对该驱动数据进行延时补偿仿真，仿真结果如图3所示。

图3 目标的真实速度与预估速度曲线Fig.3 The target velocity curve of actuality and prediction

由图可知，补偿算法较好的预估了目标运动参数。

为进一步验证补偿算法的有效性，在目标模拟器端运行该补偿算法，取延时补偿40 ms后的预估数据作为驱动数据，以标准弹道条件进行仿真测试，此时的脱靶量侧偏为1.7 m，而延时补偿前的脱靶量侧偏为3.5 m，补偿后脱靶量侧偏已大幅减小，并且小于一个像素所代表的尺寸。测试试验表明，补偿算法有效可行。

6 结论

本文通过分析目标模拟器影响红外成像制导半实物仿真全系统仿真精度的误差因素，指出红外CIG系统延时误差是红外目标模拟器影响目标特性模拟仿真精度的主要因素，并根据红外CIG延时误差的产生机理，分析了延时误差对几何分辨率、角度分辨率、动目标横向位置、动目标径向位置的影响，运用渐消记忆递推最小二乘估计算法对目标运动参数进行在线预估，建立了红外CIG系统延时误差补偿算法，该算法可以作为红外成像制导半实物仿真系统目标模拟器指标论证与仿真系统精度分析和仿真试验设计提供参考。

［1］ Sargent R G.Verification and validation of simulation models［C］.Proceedings of the 2011 Winter Simulation Conference，2011:183－198.

［2］ WANG Xiaohu，ZHANG Minglian，WU Yonggang，et al.Optimization distributing of the precision of a simulation system with hardware in the loop for infrared imagining homing missile［J］.Journal of System Simulation，1999，11(5):375－379.(in Chinese)王小虎，张明廉，吴永刚，等.红外成像自寻的制导导弹半实物仿真系统的精度最优分配［J］.系统仿真学报，1999，11(5):375－379.

［3］ SHAN Jiayuan，MENG Xiuyun，DING Yan.Hardware in the loop simulation［M］.Beijing:National Defense Industry Press，2008.(in Chinese)单家元，孟秀云，丁艳.半实物仿真［M］.北京:国防工业出版社，2008.

［4］ SU Delun，WANG Shicheng，LIAO Shouyi，et al.Dynamic infrared image generation based on CIG technology［J］.Infrafed Technology，2009，31(9):549－552.(in Chinese)苏德伦，王仕成，廖守亿，等.基于CIG的动态红外图像实时生成系统［J］.红外技术，2009，31(9):549－552.

［5］ LIU Jin－mang，LI Zhen－xing，LIU Yong－lan，et al.Algorithm to Estimate the Parametric Trajectory of elevation－only target by single station observation data［J］.Laser＆ Infrared，2012，42(11):1301－1305.(in Chinese)刘进忙，李振兴，刘永兰，等.基于单站测量的纯仰角目标参数航迹滤波方法［J］.激光与红外，2012，42(11):1301－1305.

［6］ DANG Dongni，GAO Wei，SUN Yifan.Key Technologies research for IR capturing and tracking simulation based on digital image injection［J］.Laser ＆ Infrared，2013，43(8):916－919.(in Chinese)党东妮，高卫，孙奕帆.注入式红外捕获跟踪仿真关键技术研究［J］.激光与红外，2013，43(8):916－919.

［7］ ZHOU Shanshan，CHAI Jinguang，LI Dan.A predicted tracking algorithm based on least square principle in real－time recursively［J］.Electronic Design Engineering，2011，19(10):53－55.(in Chinese)周姗姗，柴金广，李丹.实时递推的最小二乘预测跟踪算法［J］.电子设计工程，2011，19(10):53－55.

［8］ LU Zhaoquan，HU Jindong，HU Yandong，et al.Recursive fixed memory extended least squares method and simulation research［J］.Journal of Hefei University of Technology，2009，32(7):977－980.(in Chinese)鲁照权，胡金东，胡焱东，等.增广最小二乘限定记忆参数估计算法与仿真［J］.合肥工业大学学报，2009，32(7):977－980.