正方排列芯壳型平板光子晶体禁带特性的研究
胡 森, 刘 丹, 童爱红, 肖 明, 王 筠
(湖北第二师范学院 物理与机电工程学院, 武汉 430205)
正方排列芯壳型平板光子晶体禁带特性的研究
胡 森, 刘 丹*, 童爱红, 肖 明, 王 筠
(湖北第二师范学院 物理与机电工程学院, 武汉 430205)
构建了正方排列的芯壳型平板光子晶体结构,发现这种芯壳型平板光子晶体较传统的介质柱型平板光子晶体能获得更宽的类TE禁带.分析了两种模型,一种是芯层折射率为3.5,壳层折射率为2;另一种是芯层折射率为2,壳层折射率为3.5,发现当芯层折射率大于壳层折射率时,光子禁带明显增宽.
平板光子晶体; 芯壳异质结构; 光子禁带
光子晶体(Photonic Crystal,PC)的概念自提出以来,就吸引了大量科学家的目光[1-2], 光子禁带(Photonic Band Gap, PBG)是光子晶体的重要特性.光子晶体的理论体系不断完善,其应用也辐射到了更多的领域,例如,可以实现高效发光二极管、光子晶体光纤、慢光波导、全光开关及光子晶体激光器等[3].发光二极管(LED)是一种广泛应用于光电子领域的低成本、长寿命固态光源.为了取代传统照明设备,高亮度LED必须同时有高的内量子效率和外量子效率.目前,高的内量子效率可以通过先进的制作技术达到,但外量子效率因全内反射效应的影响一直不高,尤其是GaN基蓝光LED.光子晶体因其特殊性能,不仅可以提高LED的内量子效率,而且能有效提高其外量子效率.很多研究表明,在LED芯片中,制作表层光子晶体或嵌入式光子晶体,可以大大提高其外量子效率.PC LED有非常大的优越性,已成为目前国内外研究的热点[4,5].已经讨论过二维芯壳异质结构光子晶体的禁带特性,发现在介质柱外涂覆一层高折射率材料形成芯壳结构后,能获得更宽的禁带,从而有效提高LED的外量子效率[6].但是,由于二维芯壳异质结光子晶体结构实际是制造不出来的(要求第三维无限长),因此研究“芯壳型平板光子晶体”的禁带特性是非常有必要的.“芯壳型平板光子晶体”模型是在二维芯壳异质结光子晶体模型基础上而构建的,它要求介质柱有限高,其理论分析与二维芯壳异质结光子晶体非常相似.
本文首先构建了传统的平板光子晶体结构,探讨其禁带特性,发现传统的介质柱型平板光子晶体很难实现宽的类TE禁带,不能有效提高LED的外量子效率.其次构建了空气中的正方排列的芯壳型平板光子晶体模型,重点分析了两种不同的情况,第一种模型中芯层折射率大于壳层折射率,第二种模型中芯层折射率小于壳层折射率.采用平面波超晶格法来讨论其能带结构,关注其禁带特性,发现当芯层折射率大于壳层折射率时,类TE禁带明显增宽.
1 平板光子晶体禁带特征
平板光子晶体借助光子禁带控制光在平板内传播,同时平板上设置的低折射率衬底又可以靠全反射机制来阻碍光的辐射.虽然平板光子晶体与二维光子晶体有很多相似之处,可采用二维光子晶体的研究方法来理解平板光子晶体的禁带特性,但由于平板光子晶体的厚度是有限高的,因此采用平面波展开法分析平板光子晶体的能带结构时不能单纯地使用第一不可约布里渊区的概念,还需要在第三维方向上将波矢展开,也即采用修正了的平面波方法(即:平面波超晶格法)进行计算[7].
平板型光子晶体能带图有别于二维光子晶体的最重要的特征,就是具有“光锥(Light cone)”.在均匀的背景区域中,光锥线就是波矢除以折射率.光锥线以上,也即“光锥内”,表示的是一些连续态,即指包含背景中所有可能频率的连续性区域,即“泄漏模式”.光锥线以下,不连续的能带代表的是“传导模式”,简称“导模”,这些态不能和背景中的态耦合,只能在平板内无损耗的传播,一旦进入背景区域,将呈指数衰减,好似全内反射机制一样.根据导模理论可将传导模式分成两类:奇模和偶模.奇模和偶模分别与二维情形下的TM模和TE模类似,我们常称之为“类TM模式”和“类TE模式”[3].
2 传统平板光子晶体的能带结构
传统的平板光子晶体结构主要有两种,一种是介质柱型平板光子晶体,一种是空气孔型平板光子晶体,如图1所示.
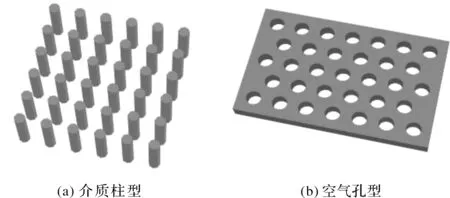
图1 传统平板光子晶体结构
图2给出的是介质柱型平板光子晶体的能带结构,其中介质柱的介电常数为12,介质柱半径为0.2a,高度为2a,且介质柱为正方排列.由图可以看出,该介质柱型平板光子晶体展现了很宽的类TM禁带,宽度约25.03%,但是类TE禁带却非常地窄,禁带大小只有6.4327%.
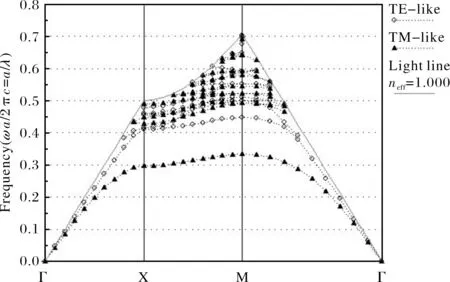
图2 介质柱型平板光子晶体的能带结构
图3给出的是空气孔型平板光子晶体的能带结构,其中基底材料的介电常数为12,空气孔半径为0.3a,且空气孔为三角排列,平板厚度为0.6a.由图可以看出,该空气孔型平板光子晶体展现了很宽的类TE禁带,宽度约26.18%,但是类TM禁带却较窄,宽度只有8.96%左右.
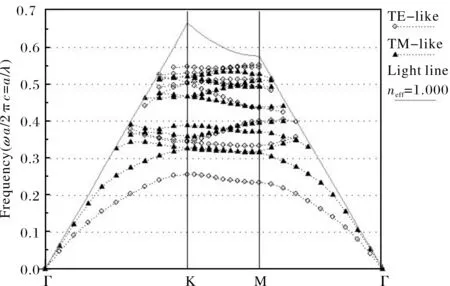
图3 空气孔型平板光子晶体的能带结构
比较以上两种传统的平板光子晶体的能带结构可知,空气孔型平板光子晶体较易产生类TE禁带,而介质柱型平板光子晶体较易产生类TM禁带,这主要是因为孤立的具有高介电常数的介质结构中容易产生类TM禁带,而连通的具有高介电常数的介质结构中容易产生类TE禁带[3].
传统的介质柱型平板光子晶体很难实现宽的类TE禁带,而发光二极管的发光中心发出的光却是类TE模式,因此要将介质柱型平板光子晶体结构应用于LED芯片之中,就必须采取某些措施使介质柱型平板光子晶体能展现较宽的类TE禁带.
3 正方排列芯壳型平板光子晶体模型
本节构建的模型为“芯壳型平板光子晶体结构”,它与二维芯壳异质结光子晶体有很多相似之处,但是在第三维方向(即z方向)上具有有限厚度.正方排列芯壳型平板光子晶体模型如图4所示.芯层介质柱半径为r,折射率为n′;覆盖层半径为R,折射率为n.介质材料在x和y方向是周期性的,晶格常数a;介质柱在z方向上有限高,高度为0.5a,且背景为空气.
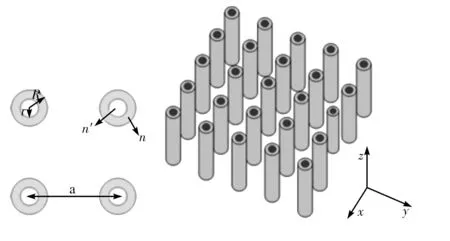
图4 正方排列芯壳型平板光子晶体
芯壳型平板光子晶体与传统的平板光子晶体最大的不同之处在于,介质柱是芯壳结构的,这样就增加了改变光子禁带宽度的参数.使介质柱的芯层和壳层之间产生了折射率差值,而这个折射率差值会在能带结构中起重要作用.
此外,讨论了两种不同结构的芯壳型平板光子晶体,介质柱均是正方排列,如图4所示.模型A对应的是芯层折射率小于壳层折射率,即n′
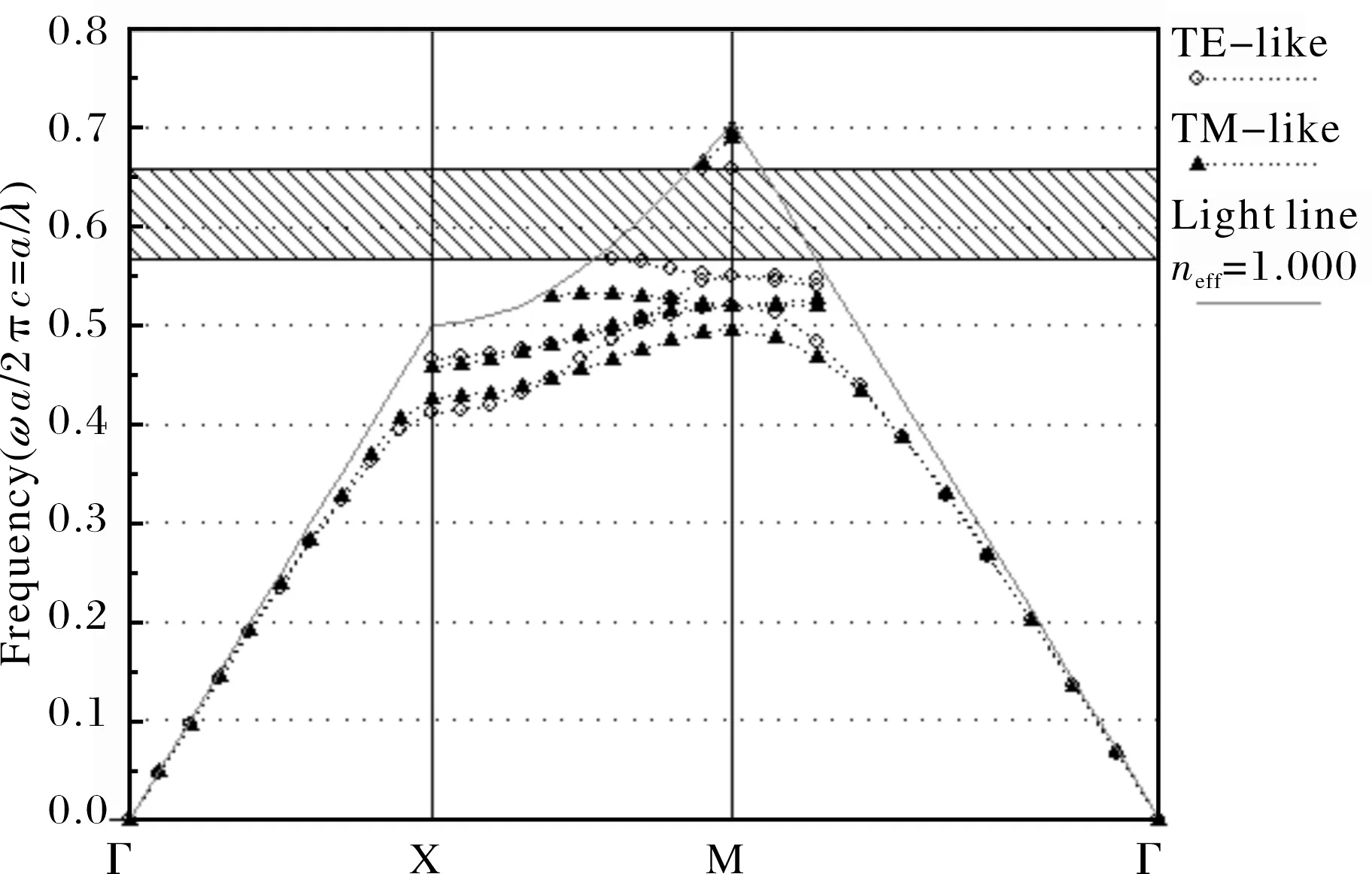
3.1 模型A(n′ 首先讨论空气中正方排列的,有限高的芯壳结构介质柱阵列,并且芯层折射率小于壳层折射率,即n′ 图5 正方排列芯壳型平板光子晶体(n′ 模型A的能带曲线如图5所示.横轴表示的是xy平面内的波矢,从左至右表示的是简约布里渊区的边界点由Γ到Χ,再到Μ.禁带宽度采用归一化频率值来表示,即Δω/ωm,表示光子晶体的能带结构的无标度性.其中ωm表示的是禁带所对应的中心频率值,而Δω表示的是禁带所对应的频率宽度.由图5可知,有一个类TE模式禁带,三个类TM模式禁带.但是,此处所指的禁带与二维光子晶体的禁带完全不同,禁带仅仅只针对导模来讲,而不包括光锥.类TE禁带频率范围是0.58~0.636ωa/2πc,禁带宽度为9.18%.第一个类TM禁带频率范围是0.559~0.636ωa/2πc,禁带宽度为12.92%;第二个类TM禁带频率范围是0.638~0.659ωa/2πc,禁带宽度为3.165%;第三个类TM禁带频率范围0.662~0.707ωa/2πc,禁带宽度为6.635%. 3.2 模型B(n′>n)的能带曲线分析 其次,讨论了空气中正方排列的,有限高的芯壳结构介质柱阵列,并且芯层折射率大于壳层折射率,即n′>n.同样,设模型B的晶格常数为a,且介质柱的高度为0.5a;芯层的半径r=0.2a, 折射率为n′=3.5(选用的是高折射率半导体材料GaAs 的折射率);壳层的半径R=0.3a,折射率为n=2(选用的是ZnO材料的折射率). 图6 正方排列芯壳型平板光子晶体(n′>n)能带图 模型B的能带结构如图6所示.由图可知,有一个类TE模式禁带,一个类TM模式禁带.类TE禁带频率范围是0.568~0.66ωa/2πc,禁带宽度为15%.类TM禁带频率范围是0.534~0.668ωa/2πc,禁带宽度为22.32%. 以上讨论了两种不同的芯壳型平板光子晶体结构,它们都是正方排列的芯壳结构纳米柱阵列,晶格常数、芯层、壳层的半径均相同.不同的是,模型A中,芯层折射率小于壳层折射率(n′=2,n=3.5);模型B中,芯层折射率大于壳层折射率(n′=3.5,n=2).模型A及模型B的禁带曲线如图5和图6所示.此处,我们特别注意“类TE模式”,因为LED的量子阱发出的光具有类似的偏振模式.模型A和模型B中都显现了一个类TE禁带,但是模型B(n′=3.5,n=2)的类TE禁带宽度(15%)远大于模型A(n′=2,n=3.5)的类TE禁带宽度(9.18%).究其原因,有几个重要因素影响光子禁带,即:对称性、材料的折射率及介质填充率[8-9].当在正方排列的有限高纳米柱外涂覆一薄层形成芯壳型平板光子晶体后,并没有改变原有结构的对称性,对称性对禁带影响可不予考虑.禁带行为就取决于材料的折射率及介质的填充率.对于传统的平板光子晶体,若介质柱与背景间的折射率差值越大,禁带越宽.介质柱折射率为3.5,高度为0.5a时,将比介质柱折射率为2,高度为0.5a的情况呈现出更宽的光子禁带.当在芯层材料为涂覆一薄层后,由于材料的填充率发生了改变,也将增大原有结构的禁带宽度,因此模型B仍将获得比模型A更宽的光子禁带. 本文构建了一种芯壳型平板光子晶体结构,即空气中的正方排列的芯壳结构纳米柱阵列,用平面波超晶格法分析其禁带特性,发现这种芯壳型平板光子晶体较传统的介质柱型平板光子晶体更能获得宽的类TE禁带.进一步讨论了两种不同情况,一种是芯层折射率大于壳层折射率,另一种是芯层折射率小于壳层折射率.通过比较它们的禁带曲线发现:当芯层折射率大于壳层折射率时,更易获得宽的光子禁带.研究结果明确了要实现宽禁带,芯层和壳层材料折射率大小选择上的原则,从而为获得高外量子效率的PC LED结构提供了理论参考. [1] Yablonovitch E. Inhibited spontaneous emission in solid-state physics and electronics[J]. Phys Rev Lett, 1987, 58(20): 2059-2062. [2] John S. Strong localization of photons in certain disordered dielectric superlattices[J]. Phys Rev Lett, 1987, 58(23): 2486-2489. [3] Joannopoulos D J, Mead D R, Winn N J. Photonic Crystals: Molding the Flow of Light[M]. Princeton: Princeton University Press, 1995. [4] Wierer J J, Krames M R, Epler J E. InGaN/GaN quantum-well heterostructure light-emitting diodes employing photonic crystal structures[J]. Appl Phys Lett, 2004, 84(19): 3885-3888. [5] Kim D H, Cho C O, Roh Y G. Enhanced light extraction from GaN-based light-emitting diodes with holographically generated two-dimensional photonic crystal patterns[J]. Appl Phys Lett, 2005, 87(20):203508-203511. [6] 刘 丹, 胡 森, 肖 明. 二维芯壳异质结构光子晶体禁带特性分析[J]. 华中师范大学学报:自然科学版, 2012, 46(6): 677-680. [7] Johnson S G, San F, Villeneuve P R. Guided modes in photonic crystal slabs[J]. Physical Review B, 1999, 60(8): 5751-5759. [8] Trifonov T, Marsal L F, Rodriguez A. Analysis of photonic band gaps in two-dimensional photonic crystals with rods covered by a thin interfacial layer[J]. Physical Review B, 2004, 70(19): 195108-195116. [9] 谢东华. 平板光子晶体的禁带特性分析[J]. 西安邮电学院学报, 2008, 13(3): 139-142. The investigation on photonic band-gap in square core-shell type photonic crystal slabs HU Sen, LIU Dan, TONG Aihong, XIAO Ming, WANG Yun (Department of Physics and Electronics, Hubei University of Education, Wuhan 430205) A core-shell type photonic crystal slab with a square lattice is studied. The results present that the core-shell type photonic crystal slab can obtain wider TE band gaps than the traditional photonic crystal slab with rods in air. Two models have been analyzed. One is that the refractive index of the core is 3.5, and the refractive index of the shell is 2. The other is that the refractive index of the core is 2, and the refractive index of the shell is 3.5. The study reveals that the photonic band gap is considerably enhanced in size when the refractive index of the core is larger than the shell. photonic crystal slab; core-shell type structure; photonic band-gap 2014-04-10. 国家自然科学基金理论物理专款项目(11347189);湖北省自然科学基金项目(2013CFB015). 1000-1190(2015)01-0034-04 O734 A *通讯联系人. E-mail: liudan725@126.com.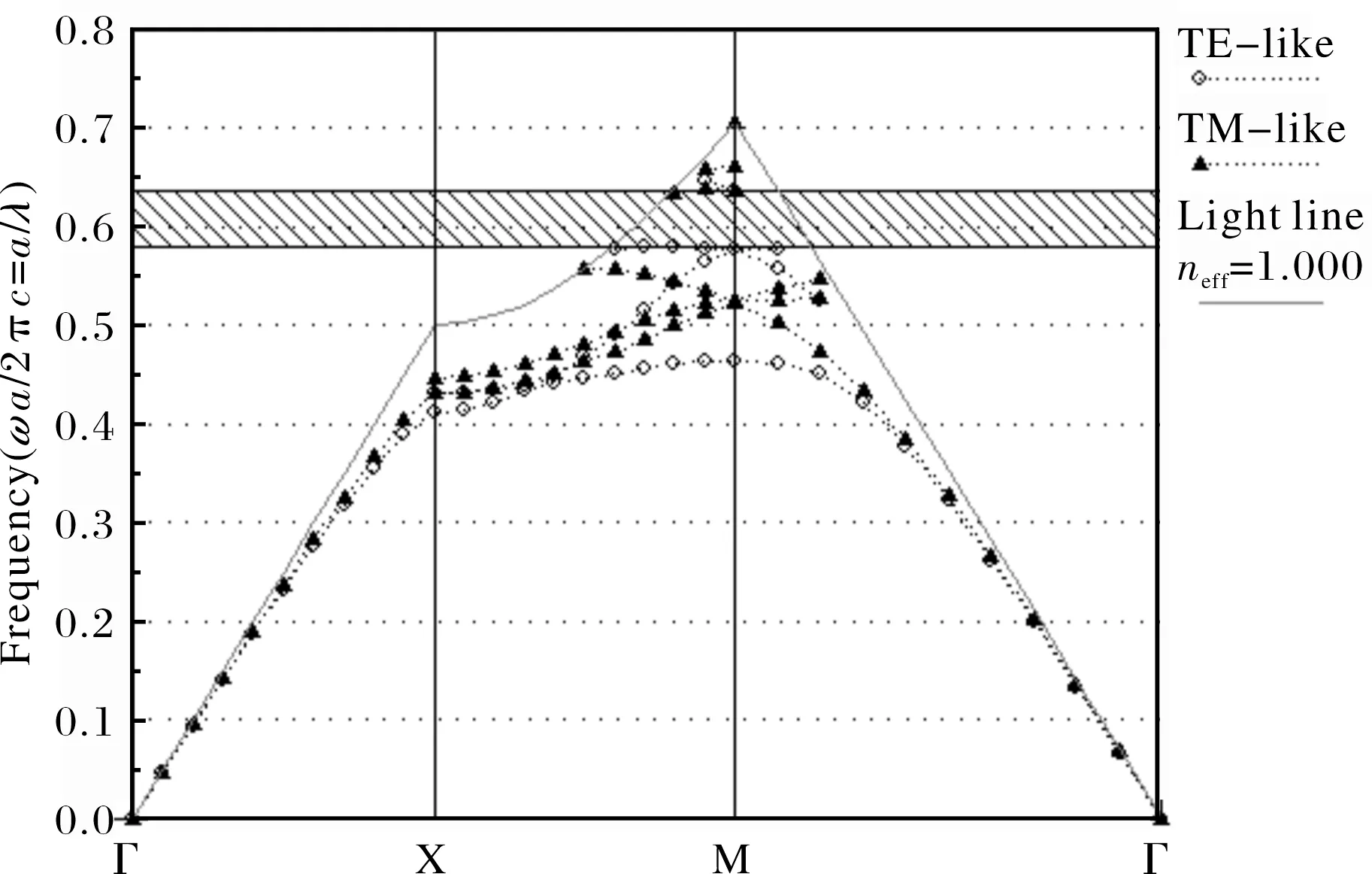
4 结论

