矿井大型导线控制网双观测平差模型

于瑞鹏 林 卉 丁 翠 王李娟 孙华生

(1.山东省第一地质矿产勘查院，山东 济南 250014；2.江苏师范大学测绘学院，江苏 徐州 221116；3.山东城市建设职业学院，山东 济南 250103；4.辽宁工程技术大学测绘与地理科学学院，辽宁 阜新 123000)

矿井大型导线控制网双观测平差模型

于瑞鹏1林 卉2丁 翠3王李娟2孙华生4

(1.山东省第一地质矿产勘查院，山东 济南 250014；2.江苏师范大学测绘学院，江苏 徐州 221116；3.山东城市建设职业学院，山东 济南 250103；4.辽宁工程技术大学测绘与地理科学学院，辽宁 阜新 123000)

矿井导线网平差的特点是2类观测值(测角和量边)数量相当，多余观测量相对较少。为了提高矿井大型导线控制网的平差精度，根据矿井导线控制网往返观测及验后估计需要多余观测数较多的特点，提出了双观测平差模型。相对于经典平差模型，该模型条件方程个数较多，容易满足验后估计的可估条件，从而可通过后验估计合理定权来提高矿井大型导线控制网的平差精度。以某矿井大型导线控制网的实测数据为例进行了平差计算，结果显示：经典平差模型求得的3条已知边的方位角平差值与真值之差依次为-7″、-62″、-54″，而新提出的双观测平差模型所得出的平差值与真值之差依次为-10″、-12″、-15″，这说明双观测平差模型通过Helmert方差估计能够合理定权，可更准确地计算出各网点的平差值，具有一定的实用性。

导线控制网平差 双观测平差模型 Helmert方差估计 精度

矿井控制网由于受巷道条件的限制，均以导线的形式沿巷道布设[1]。在控制网施测过程中需要沿导线布设路线对角度和边长进行往返观测，在控制网平差时一般取往返观测值的算术平均值为最终观测值，按照条件平差法进行控制网平差[1-6]。该平差模型的缺点是条件方程个数较少，即多余观测数较少，从而很难满足验后估计的可估条件。在确定矿井控制网平差的随机模型时，对于测角、量边等2类不同的观测量一般采用经验公式定权，即根据仪器出厂标明的标称精度和导线网的等级来确定各自的方差，在此基础上确定各自的权重。实践证明，经验公式定权在许多情况下是不够精确的，尤其是控制网形较大的情形，该定权方法适用性较差[7-9]。随着井田的开拓，井下控制网的规模也随之扩大。为了提高控制网平差结果的可靠性，Helmert于1924年提出了一种验后估计方差法，即Helmert方差估计法，此后许多学者对其进行了扩展或简化，并进行了大量应用研究[10-16]。只有在控制网形较大，多余观测数较多且各类观测值的多余分量大体保持相等的情况下，进行Helmert方差估计才是必要的和有利的。也就是说，一个控制网能否进行验后估计取决于其控制网形结构及观测水平[5]。矿井导线网平差的特点是2类观测值(测角和量边)数量相当，多余观测量相对较少。本研究充分利用矿井导线返测可增加多余观测值的特点，建立了双观测平差模型，该模型的条件方程个数较多，容易满足Helmert方差估计的可估条件，从而可通过验后估计合理定权来提高矿井大型控制网的平差精度。

1 双观测平差模型

矿井控制网一般以闭合导线或附合导线的形式布设，每一条闭合或附合导线都存在3个条件方程，即1个方位角条件方程、2个坐标条件方程，因此，控制网平差时采用条件平差法比较方便。 设L1、L2分别为互相独立的角度、边长观测向量，相应的改正数向量分别为V1、V2，相应的对角权阵分别为P1、P2，则条件平差法的数学模型为[17-19]

A1V1+A2V2=W，

(1)

式中，A1,A2分别为角度、边长的系数矩阵；W为平差系数矩阵。式(1)为往测或往返测取观测值平均值时对应的条件平差模型，对应的多余观测数为r个。

双观测平差模型充分利用了往返观测值，当矿井导线采用了往返观测或部分路线采用了往返观测时，设返测时共观测了m个值，其中m1个角度观测值向量为L1′，m2(m2=m-m1)个边长观测值向量为L2′，相应的改正数向量分别为V1′、V2′，对应的对角权阵分别为P1′、P2′，令

则m个观测值的条件平差模型为

(2)

令

联合式(1)、式(2)，可得整个控制网条件方程为

(3)

若令

则式(3)可表示成

(4)

式(4)包含了全部或部分观测量的双观测值，即为双观测平差的函数模型，对应的多余观测数为(r+m)个。

2 双观测平差模型验后估计

由(4)式可得其法方程为[8]

(5)

式中，K为法方程系数矩阵；

于是，各观测值的改正数方程为

(6)

式(4)共有(r+m)个条件方程，即双观测平差模型共有(r+m)个多余观测量。为了准确确定矿井大型控制网中测角和量边等2类观测值对应的权重，需要利用验后估计法重新定权。现有研究表明：对含有2类观测值的方差分量估计的必要多余观测数应大于20。显然，在矿井控制网双观测平差时很容易满足上述多余观测量条件，从而可用Helmert方差估计法对测角和量边进行验后定权[20]。以新的权重重新行平差计算，经多次迭代，直至各观测值单位权方差之比为1为止。

3 应用实例

某矿井大型控制网由146个网点组成，近井1、近井2为已知点，导线总长约11.3km。按照7″级导线布设，加测了3条陀螺边，分别为A4—A5、A22—B1、E9—E10，各陀螺边与起算点间的相对位置见图1，陀螺方位角观测结果见表1。观测路线：近井2—L1—L2—X1—X2—X3—X4—X5—X6—A5—A4进行了往返观测，返测该路线时共观测了10个角度、10条边长。

图1 陀螺边与起算点间的相对位置示意Fig.1 Relative position between gyro-sideand starting calculating points表1 陀螺边方位角观测成果Table 1 Surveying results of orientationangle of each gyro-side

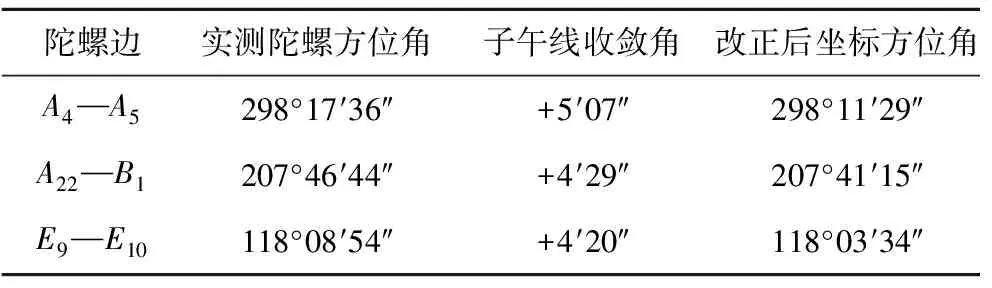
陀螺边实测陀螺方位角子午线收敛角改正后坐标方位角A4—A5298°17′36″+5′07″298°11′29″A22—B1207°46′44″+4′29″207°41′15″E9—E10118°08′54″+4′20″118°03′34″

为了比较Helmert方差估法与经典平差模型的平差精度，3个陀螺方位角观测值不参与平差计算，仅用来比较不同方案计算出的该3条陀螺边方位角的平差值。

(1)方案1。经典平差法定权时，设测角中误差(σ01=7″)为单位权中误差，各边的量边中误差根据仪器的标称精度公式计算，各角度观测值的权重为1，各边长观测值的权重为PSi。列出双观测值平差的函数模型，多余观测量为37，在此基础上根据条件平差公式求得各参数的最小二乘解。

(2)方案2。在经典平差模型的基础上，计算经典平差模型对应的角度、边长单位权方差的估值，单位权中误差的估值为11.7″，经3次迭代定权，采用Helmert方差估计法使得单位权方差之比约为1。

2种方案计算的各陀螺边端点坐标平差值见表2，各已知陀螺边方位角的平差结果见表3。

表2 2种方案中各陀螺边端点坐标平差值

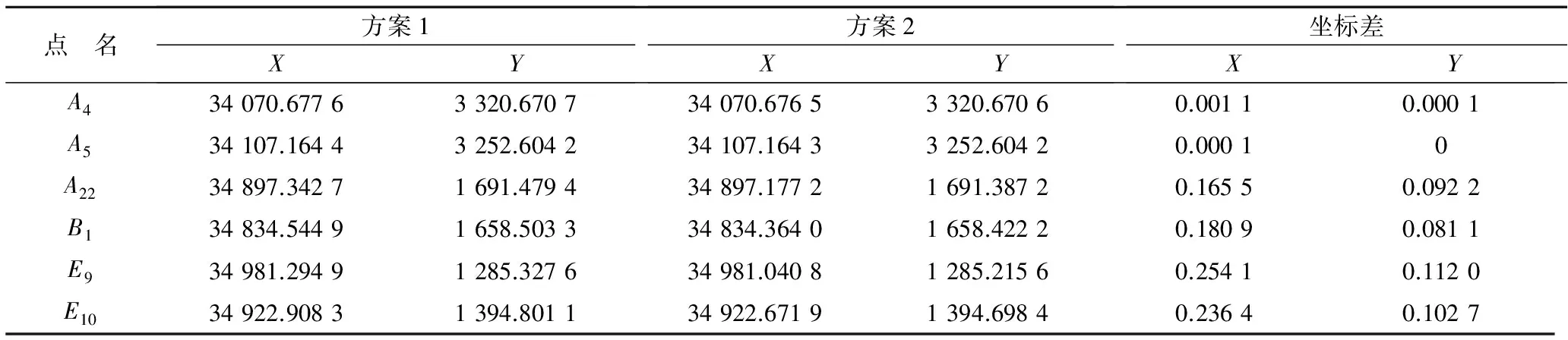
Table 2 Adjustment values of endpoint coordinates of gyro-side of two schemes m

表3 2种方案各陀螺边方位角平差结果Table 3 Adjustment values of orientation angleof each gyro-side of two schemes

由表2可知：距起算点越远坐标差值越大，由于起算点到A4—A5路线采用了往返观测，且A4、A5点距起算点较近(约900 m)，2种方案计算的A4、A5点的坐标基本一致；E9、E10点距起算点约5 km，该2点的X坐标差值均超过20 cm，说明观测的权重对平差结果有一定的影响，在矿井大型控制网平差中，该影响不容忽视。

由表3可知：经典平差模型计算的方位角与实测值相差较大，而本研究提出的双观测平差模型计算出的方位角与实测值相差较小，说明本研究采用的Helmert方差估计法能够合理定权，有助于提高矿井导线控制网的平差精度。

4 结 论

(1)观测值的权重对单位权中误差的估值影响很大，本研究中经典平差时单位权中误差的估值为11.7″，而Helmert方差估计法对应的单位权中误差的估值为5.2″，说明该方法提高了矿井大型导线控制网的平差精度。

(2)双观测平差模型充分利用了矿井导线控制网的往返观测数据，使得平差模型中具有较多的条件方程，能够满足验后估计的可估条件。

(3)当矿井导线控制网规模较大时，先验定权法往往很难满足平差要求，而双观测平差模型通过验后估计合理定权可更准确地计算出各网点的平差值，为设计矿井大型导线控制网施测方案提供了依据。

[1] 张国良，朱家钰，顾和和.矿山测量学[M].徐州：中国矿业大学出版社，2006. Zhang Guoliang,Zhu Jiayu,Gu Hehe.Mine Surveying[M].Xuzhou：China University of Mining and Technology Press,2006.

[2] 贾宝新，李国臻.矿山地震监测台站的空间分布研究与应用[J].煤炭学报，2010，35(12)：2045-2048. Jia Baoxin,Li Guozhen.Research and application of spatial distribution of mines seismic monitoring stations[J].Journal of China Coal Society,2010,35(12)：2045-2048．

[3] 周志辉.三维数字化矿山信息系统的动态更新与应用[J].现代矿业，2014(5)：11-15. Zhou Zhihui.Dynamic updating and application of the 3D digital mine information system[J].Modern Mining,2014(5)：11-15.

[4] 蒋 晨，张书毕.基于VB的TM30 测量机器人变形监测系统开发[J].金属矿山，2015(1)：104-107. Jiang Chen,Zhang Shubi.Development of the deformation monitoring system of TM30 measuring robot based on VB[J].Metal Mine,2015(1)：104-107.

[5] 吴立新，汪云甲，丁恩杰，等.三论数字矿山——借力物联网保障矿山安全与智能采矿[J].煤炭学报，2012，37(3)：357-365. Wu Lixin,Wang Yunjia,Ding Enjie,et al.Thirdly study on digital mine：serve for mine safety and intellimine with support from internet of tings[J].Journal of China Coal Society,2012,37(3)：357-365．

[6] 徐凯帆，张书毕，鲍 国.附加约束条件的井下控制网变参数序贯平差[J].金属矿山，2015(6)：103-107. Xu Kaifan,Zhang Shubi,Bao Guo.Variable parameter sequential adjustment with constrained condition of underground control network[J].Metal Mine,2015(6):103-107.

[7] Teunissen P J,Amiri-Simkooei A R.Least-squares variance component estimation[J].Journal of Geodesy,2008(2):65-82.

[8] 崔 清，陈 曦，贾旭光，等.基于测距技术的边坡角测定误差及敏感性分析[J].金属矿山，2014(5)：121-124． Cui Qing,Chen Xi,Jia Xuguang,et al.Slope angle measuring error and sensitivity analysis based on the distance measurement technology[J].Metal Mine,2014(5)：121-124.

[9] 武继军，胡圣武.测量平差的基准方程与相对形变及其精度分析[J].煤炭学报，2007，32(8)：808-812. Wu Jijun,Hu Shengwu.Surveying adjustment datum and relative deformation accuracy analysis[J].Journal of China Coal Society,2007,32(8)：808-812．

[10] 高俊强，胡 灿.Helmert方差分量估计在隧道贯通中控制网平差的研究[J].中国矿业大学学报，2006，35(1)：125-129. Gao Junqiang,Hu Can.Study of Helmert variance component estimation in tunnel run-through control traverse difference[J].Journal of China University of Mining and Technology,2006,35(1)：125-129．

[11] 黄维彬.近代平差理论及其应用[M].北京：解放军出版社，1992. Huang Weibin.Modern Adjustment Theory and Its Application[M].Beijing：People′s Liberation Army Press,1992.

[12] 张书毕.测量平差[M].徐州：中国矿业大学出版，2012. Zhang Shubi.Surveying Adjustment[M].Xuzhou：China University of Mining and Technology Press,2012.

[13] Strang G,Borre K.Linear Algebra Geodesy and GPS[M].Massachusetts：Wellesley-Cambridge Press,1997.

[14] Neitzel F.Generalization of total least-squares on example of unweighted and weighted 2D similarity transformation[J].Journal of Geodesy,2010,84(9)：751-762.

[15] 卞和方，张书毕，李益斌，等.概括平差模型的通用解法[J].测绘科学，2009，34(6)：35-36. Bian Hefang,Zhang Shubi,Li Yibin,et al.A universal solution for generalization adjustment model[J].Science of Surveying and Mapping,2009,34(6)：35-36．

[16] Yu Z C.A universal formula of maximum likelihood estimation of variance-covariance components[J].Journal of Geodesy,1996(7)：233-240.

[17] 李保学.陀螺方位附合导线在矿井测量中的应用[J].煤炭技术，2015，34(2)：73-74. Li Baoxue.Application of gyro azimuth in mine traverse measurement[J].Coal Technology,2015,34(2)：73-74.

[18] 马 洋，欧吉坤，袁运斌.采用联合平差法处理附有病态等式约束的反演问题[J].武汉大学学报：信息科学版，2011，36(7)：816-819. Ma Yang,Ou Jikun,Yuan Yunbin.Solving equality constraint inversion with ill-posed constraint matrix using united method[J].Geomatics and Information Science of Wuhan University,2011,36(7)：816-819.

[19] 葛旭明，伍吉仓.病态总体最小二乘问题的广义正则化[J].测绘学报，2012，41(3)：372-377. Ge Xuming,Wu Jicang.Generalized regularization to ill-posed total least squares problem[J].Acta Geodaetica et Cartographic Sinica,2012,41(3)：372-377.

[20] 李 斐，郝卫峰，王文睿，等.非线性病态问题解算的扰动分析[J].测绘学报，2011，40(1)：1-5. Li Fei,Hao Weifeng,Wang Wenrui,et al.The perturbation analysis of nonlinear ill-conditioned solution[J].Acta Geodaetica et Cartographic Sinica,2011,40(1):1-5.

(责任编辑 王小兵)

Dual-observation Adjustment Model of Undermine Large Traverse Control Network

Yu Ruipeng1Lin Hui2Ding Cui3Wang Lijuan2Sun Huasheng4

(1.TheFirstInstitutionofGeo-explorationofShandongProvince,Jinan250014,China;2.SchoolofGeodesyandGeomatics,JiangsuNormalUniversity,Xuzhou221116,China;3.ShandongUrbanConstructionVocationalCollege,Jinan250103,China;4.SchoolofGeomatics,LiaoningTechnicalUniversity,Fuxin123000,China)

The quantity of two types of observation values are closely with each other and the additional observation values is relatively few,which are the obvious characteristics of undermine transverse adjustment.In order to improve the precision and reliability of the undermine large and control network,the dual-observation adjustment model is proposed based on the characteristics of the direct and reversed observation of undermine transverse control network and the more redundant observation required by posterior estimation.Compared with the classical adjustment models,the dual-observation adjustment model is characterized by more condition equations and easier to meet the estimation condition of posterior estimation,and then the precision can be effectively improved by determining the proper weight value by using posterior estimation.Taking the measure data of the undermine large traverse control network of a mine as the research example,the adjustment calculation is conducted,the results show that the difference between the azimuth angle adjustment values of the three known sides obtained by using the classical adjustment model and the true values are -10″,-12″,-15″respectively,the differences of the adjustment values obtained by the dual-observation adjustment model proposed in this paper and the true values are -10″m,-12″,-15″respectively,it is further indicated that the dual-observation adjustment model proposed in this paper can improve the precision and reliability of the nodes of the undermine large traverse control network by determining the reasonable weight values based on Helmert variance estimation method,therefore,it has some practical value to improve the adjustment precision of the undermine large traverse control network.

Traverse control network adjustment,Dual-observation adjustment model,Helmert variance estimation,Precision

2015-08-07

国家自然科学基金项目(编号：41401397，41201454)，江苏省自然科学基金青年基金项目(编号：BK20140237)，现代工程测量国家测绘地理信息局重点实验室项目(编号：TJES1204)。

于瑞鹏(1982—)，男，工程师，硕士。通讯作者 林 卉(1973—)，男，副教授，硕士研究生导师。

TD172

A

1001-1250(2015)-11-109-04