矿山爆破效果的可拓学评价

张建华 李泽安 周乐静怡

(1.武汉理工大学资源与环境工程学院，湖北 武汉 430070；2.武汉大学数学与统计学院，湖北 武汉 430072)

矿山爆破效果的可拓学评价

张建华1李泽安1周乐静怡2

(1.武汉理工大学资源与环境工程学院，湖北 武汉 430070；2.武汉大学数学与统计学院，湖北 武汉 430072)

针对目前矿山爆破效果评价的特点，引进可拓理论对黄麦岭磷矿某台阶爆破效果进行评价。选取爆破质量、爆破安全和爆破技术经济效益3个方面作为一级评价指标，松散系数、大块率、根底率、前冲情况、后冲情况、爆破震动、飞石距离、炸药单耗和每米崩矿量等9个方面作为二级评价指标。计算结果表明：该次矿山爆破爆破质量处于良的范围内，爆破安全、爆破经济效益和最终的爆破效果都处于“优”的范围内。最后将此次爆破效果评价结果与实际情况相比较，得到其与实际情况相一致。因此，将可拓学理论运用到矿山爆破效果评价中是可行的，具有工程应用价值。

可拓学理论 矿山爆破 爆破效果 评价体系

矿山爆破是矿山生产过程中不可或缺的一个环节，爆破效果的好坏将直接影响到矿山后续工艺、工程质量、经济效益和安全等[1]。因此，通过一种科学的评价方法来评价爆破效果，从而选定最优的爆破方案是每一个矿山生产企业或矿山爆破施工管理者的基本义务。

评价矿山爆破效果的方法有多种，如灰色关联分析、Rs-Topsis、模糊评价和神经网络等[2]，而其中模糊评价是应用最广和研究最多的方法。如蒲传金、肖正学等[3]将层次分析法与模糊数学结合对某露天矿爆破效果进行模糊评价，其结果与实际相一致；秦虎、汪旭光等[4]运用模糊评价法评价某露天矿台阶爆破效果，取得了很好的效果。这都说明模糊评价可以很好地评价出矿山爆破效果。但该方法存在重大缺陷，其隶属度函数不能取极值，这也就说明模糊评价存在掩盖极值的问题[5-6]。为了解决这一问题而又可以继承模糊评价的优点，本研究尝试将可拓学应用到矿山爆破效果评价中，希望提出一种评价爆破效果的新方法。

1 爆破效果评价体系的构建

根据爆破指标的性质和特点，把它们划分为爆破质量、爆破安全和爆破技术经济效益3个方面[7]，又可细分为松散系数、大块率、根底率、前冲情况、后冲情况、爆破震动、飞石距离、炸药单耗和每米崩矿量等9个方面。因此,根据以上层次划分结果可以构建出爆破效果层次结构模型，划分结果见表1。

表1 某矿山爆破效果层次结构模型Table 1 Blasting effect hierarchical structural model

2 爆破效果的可拓综合评价模型

可拓综合评价的基本思想：根据所掌握的资料，对评价对象的等级进行划分，综合专家意见和实际情况给出各等级的取值范围，再将评价对象的实际数据代入各等级中进行评价，评价结果根据实际数据与各等级集合的综合关联度大小确定，综合关联度越大，表明该评价对象隶属于该等级的可能性越高[8]。

2.1 爆破效果评价标准的建立

由于可拓综合评价法是根据关联度、关联函数、经典域、节域等内容进行评价的[6]，而这些内容计算结果正确与否都跟指标等级划分标准的准确性有很大关系，因此能否构建合理且正确的评价标准，将直接影响到评价结果的可信度和准确性。爆破效果评价等级分为“优”、“良”、“一般”和“差”4个等级，其中二级评价指标等级取值范围见表2。

表2 评价等级指标Table 2 Evaluation index level

注：表中b为爆堆宽度，B为台阶面边缘到最后排炮孔宽度，具体取值范围可根据实际情况适当改变。

2.2 爆破效果可拓综合评价建模过程

(1)确定爆破效果等级集合U和评价指标集合C。爆破效果等级集合为U={U1，U2，U3，U4}={优，良，一般，差}；一级指标评价指标集合为C={C1，C2，C3}={爆破质量，爆破安全，爆破技术经济效益}。

(2)确定物元经典域Rj和节域RU。令

(1)

式中，Vj为评价指标集Ci关于爆破效果等级Uj所规定的量值范围，称之为经典域，j=1,2,3,4；cin为评价指标集Ci下所属的二级评价指标，i=1,2,3；ajn，bjn分别表示二级指标cin量值范围的上界和下界。

令

(2)

式中，VU表示评价指标集C关于全部等级U所规定的量值范围，即U的节域。

根据以上公式就可以确定经典域和节域。

(3)确定待评价对象。待评价对象用Ri表示，

(3)

式中，Pi为待评对象；vip为Pi关于cip的量值，即待评物元的实际数据。

(4)确定各级评价指标权重。由于各个指标对爆破效果所起的作用并不是完全相同的，因此为了体现各个指标重要程度的差异性，在确定评价体系后，应对各指标的权重进行赋值。权重的确定可以采用AHP法、熵权法、专家评分法等。采用层次分析法计算指标权重，具体计算过程从略，计算结果见表3。

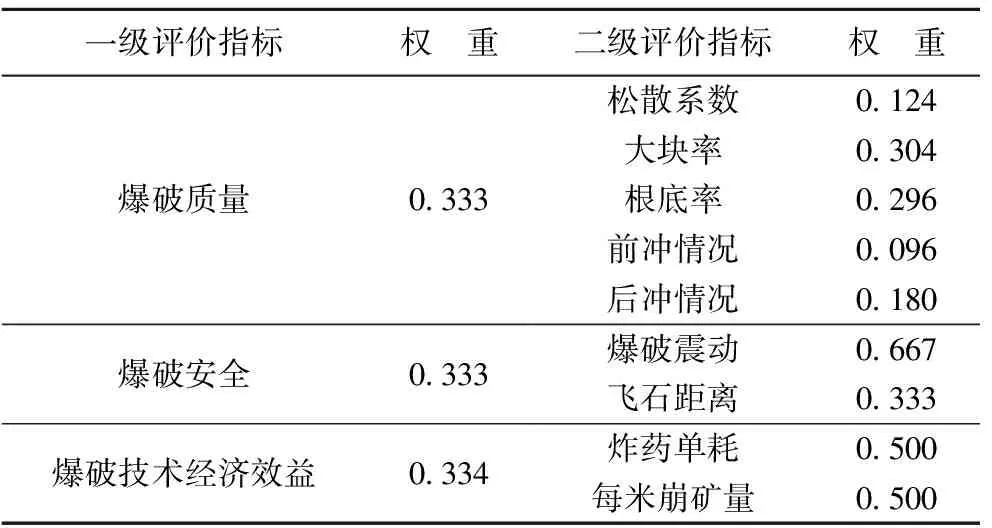
表3 矿山爆破效果评价指标权重Table 3 Evaluation index weight

(5)建立关联函数，计算关联度及规范化。根据以下公式确定各等级的关联度。

(4)

式中，kj(vik)为第i个1级指标中第k个2级指标关于效果等级j(j=1，2，3，4)的关联度；

为了便于比较分析，需对关联度进行规范化处理。规范化处理方法有很多种，这里采用最大值法，即

(5)

(6)计算评价对象的综合关联度。

(6)

式中，∂i为第i个指标的权重。

3 实例分析

将建立的可拓综合评价模型应用于黄麦岭磷矿东坑采场某次台阶爆破中。

前叙已经确定了爆破效果等级域U、评价指标集C和各级评价指标权重，因此现只需确定经典域和节域，以及待评价对象。

3.1 确定经典域Rj和节域RU

根据表2可以确定经典域Rj和节域RU。以C1(爆破质量)为例。其各等级经典域为

其节域为

3.2 确定待评价物元

待评价物元振动分值根据爆心距为100、200、300 m这3处最大振速所得分值加权计算得到。根据黄麦岭现场的情况，分别给出不同爆心距的权重，然后将实测的振速与萨道夫公式计算得到的理论值进行比较，确定所得分值

v6=0.4×9.5+0.3×9.2+0.3×9.4=9.38.

详见表4。

表4 爆破振动评价Table 4 Blasting vibration evaluation

其他8个评价指标根据爆破现场实际情况得出，得出的最终实测评价向量为

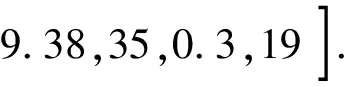
因此对于指标集C1的待评价物元为

3.3 计算关联度

以计算c11松散系数为例：

则可得

同理可计算其他隶属于C1的二级指标的关联度，得到关于C1关联度矩阵为

采用最大值法对得到的关联度矩阵进行规范化，得到

3.4 计算评价对象的综合关联度

根据综合关联度函数，代入数据得

kc1=(-0.266，0.324，-0.411，-0.843).

同理计算C2、C3可得

kc2=(0.993，-0.290，-0.573，-0.689)，

最终爆破效果关联度

3.5 结果分析

将kc1、kc2、kc3计算结果结合最大隶属度原则，可以确定其值分别为0.324，0.993，0.325，说明爆破质量处于“良”的范围内，爆破安全和爆破经济效益都处于“优”的范围内。

同理可得kc的值为0.351，即说明此次爆破效果评价结果为“优”。与实际爆破情况相比较，认为该次评价结果与实际情况相符。

4 结 语

矿山爆破效果可拓综合评价法将多指标、多因素的评价和决策转化为单目标、单因素的评价和决策，评价结果以定量的形式表示，能较全面地反映出矿山爆破存在的问题或需要改进之处，然后根据存在的问题改进爆破设计，从而达到良好的爆破效果。

将建立好的可拓模型运用到黄麦岭磷矿东坑采场某次台阶爆破中，其评价结果表明爆破质量处于“良”的范围内，爆破安全、爆破技术经济效益和最终爆破效果评价结果都处于“优”的范围内，且与实际爆破情况相一致。

将可拓理论应用到矿山爆破效果评价中是可行的，具有工程应用价值。

[1] 王 员.露天矿山爆破作业模糊综合评价应用研究[D].成都：西南交通大学,2014. Wang Yuan.Research on Application of Fuzzy Comprehensive Evaluation Surface Mine Blasting Operation[D].Chengdu:Southwest Jiaotong University,2014.

[2] 曾新枝，房泽法.矿山爆破效果综合评价的现状[C]∥中国采选技术十年回顾与展望.北京：冶金工业出版社，2012. Zeng Xinzhi,Fang Zefa.Situation Evaluation of mine blasting effect[C]∥Chinese Mining Technology Review and Outlook.Beijing:Metallurgical Indurstry Press,2012.

[3] 蒲传金，肖正学，郭学彬.爆破效果综合评价的模糊层次分析法模型[J].矿业快报，2004,20(11)：11-15. Pu Chuanjin,Xiao Zhengxue,Guo Xuebin.Model of fuzzy hierarchy analysis process for comprehensive evaluation of blasting effect[J].Mining Industry,2004,20(11)：11-15.

[4] 秦 虎，汪旭光.爆破效果综合评价的模糊数学模型[J].工程爆破，1997(3)：5-10. Qin Hu,Wang Xuguang.Fuzzy mathematics model of comprehensive evaluation of blasting results[J].Engineering Blasting，1997(3)：5-10.[5] 刘 烜.基于可拓学理论的边坡稳定性评价研究[D].北京:北京交通大学,2009. Liu Xuan.Research on Slope Stability Evaluation Based on Extension Theory[D].Beijing：Beijing Jiaotong University,2009.

[6] 赵永春.基于可拓学的地铁运营安全评价研究[D].北京：北京交通大学,2012. Zhao Yongchun.Study of the Safety Evaluation of Urban Subway Operation Based on Extenics[D].Beijing:Beijing Jiaotong University,2012.

[7] 张建华，夏岸雄，王 涛.逐孔起爆爆破效果的模糊综合评价[J].爆破，2013,30(4)：83-86. Zhang Jianhua,Xia Anxiong,Wang Tao.Blasting effect of hole-by-hole initiation based on fuzzy complex evaluation[J].Blasting,2013,30(4):83-86.

[8] 李栋学，刘 茂，刘付衍华.基于多层次可拓评价法的城市燃气管线风险评价研究[J].防灾减灾工程学报，2010(1)：92-97. Li Dongxue，Liu Mao，Liu Fuyanhua.Multilevel extension assessment method of city gas pipeline risk assessment[J].Journal of Disaster Prevention and Mitigation Engineering,2010(1):92-97.

(责任编辑 徐志宏)

Extension Theoretical Evaluation of Mine Blasting Effect

Zhang Jianhua1Li Zean1Zhou Lejingyi2

(1.SchoolofResourcesandEnvironmentalEngineering，WuhanUniversityofTechnology，Wuhan430070，China；2.MathematicsandStatisticalInstitute，WuhanUniversity，Wuhan430072，China)

Aiming at the characteristics of mine blasting effect evaluation，the extension theory is introduced to evaluate the bench blasting effect in Huangmailing Phosphate Mine.Three parameters of blasting quality，safety and technical and economic benefits are selected as first-rank evaluation indexes.Nine parameters of loose coefficient，boulder yield，toe rate，foreward，backward，blasting vibration，fly rock distance，explosives specific consumption and ore caving amount per meter is considered as second-rank evaluation indexes.The calculation results show that：the blasting quality is within the range of good，and blasting safety，economic efficiency and ultimately blasting effect all are within the range of excellent.Finally，comparison of the blasting evaluation results with the actual situation shows that it is consistent with the actual situation.Therefore，the application of extension theory to evaluating mine blasting effect is feasible，and has engineering application value.

Extension theory，Mine blasting，Blasting effect，Evaluation system

2015-09-10

张建华(1963—)，男，教授，博士，博士研究生导师。

TD235.5

A

1001-1250(2015)-11-033-04