基于工程加权分配法的励磁调节器可靠性设计

陈国玉

（青海民族大学交通与工程系，青海 西宁 810007）

引言

励磁调节器是励磁控制系统的控制中枢，性能优良、运行稳定的励磁调节器对同步发电机乃至整个电力系统十分重要，可靠性也是励磁调节器中最重要的指标［1］。目前，高科技技术的广泛应用，使得励磁系统达到了前所未有的智能化程度。然而智能化水平的提高却并不意味着产品可靠性的增长。因此，在提高产品智能化水平的同时，如何提高产品的可靠性，进行可靠性分配和预计显得非常重要。

提高励磁调节器的可靠性有两个方面：提高装置本身的抗干扰能力；增加冗余装置［2］。系统可靠性分配是，将使用方在装备设计任务书中提出的可靠性指标，并将指标自上而下、由大到小、由整体到局部逐步分解，分配到各系统、分系统及设备中［3］。可靠性分配的方法有很多，如比例分配法、最少工作法、AGREE分配法、评分分配法等。所有方法各有优劣，工程加权分配法是王锡吉教授在AGREE分配法的基础上提出来的［4］，在设计阶段分析产品可能达到的可靠性水平，从定性到定量分析就是可靠性预计，是研究可靠性工程的基础。

1 励磁调节器的可靠性模型的建立

根据系统可靠性结构模型，该励磁调节器具体可分为：测量单元、励磁调节单元、脉冲放大单元、通讯单元、电源单元共5大单元，该系统为混合结构复杂串、并联系统结构图如图1所示。

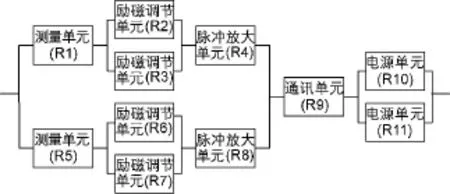
图1 复杂串、并联系统结构图

可靠度分解计算：

1）计算分系 统R1、R2－3、R4的 串联可 靠度R1－4，得：

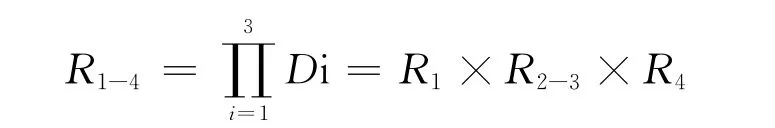
2）计算分系统R5、R6－7、R8的串联可靠度R5－8，得：

3）计算R1－4、R5－8两个分系统并联的可靠度：

4）计算R10、R11两个分系统并联的可靠度：

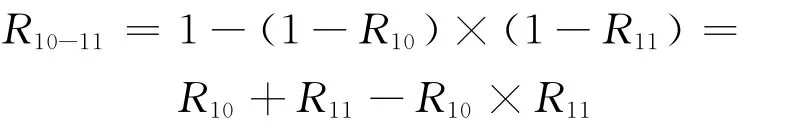
5）整个系统的可靠度RS由R1－8、R9、R10－11串联计算可得：

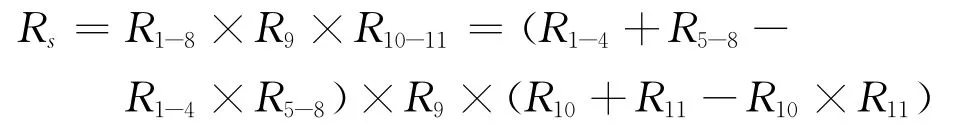
2 励磁调节器的可靠性分配

根据励磁系统在电站的使用要求，某大型火电机组一次不间断运行的时间往往可达半年，按180d计算，即4 320h。根据可靠性要求，励磁系统运行4 320h可靠度应达0.9，计算可得励磁系统的平均无故障时间要求为：

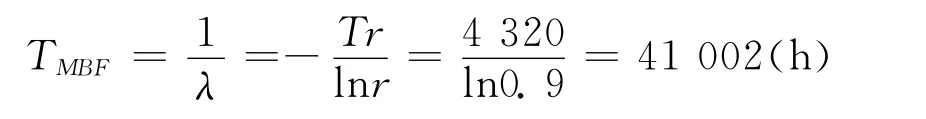
为留足够余量，励磁调节器的平均无故障时间（TMBF）往往按50 000h计算。产品的可靠性分配是指按产品总体可靠性的要求，把可靠性指标合理的分配到每个子系统，特别是对平均无故障时间的分配。以某型励磁调节器为例，该系统是一个由测量、调节、通讯等多个分系统组成的复杂系统，为达到平均无故障时间（TMBF）50 000h的要求，需对各分系统进行可靠性分配。在系统可靠性分配时使用加权因子分配法，工程加权分配法通常需要考虑的加权因子有重要因子、复杂因子、环境因子、标准化因子、维修因子和元器件质量因子等［5］。

1）考虑到该系统为混合型结构模式，先对R1－8、R9、R10－11三个串联分系统进行可靠性分配，各加权因子取值（如表1）。

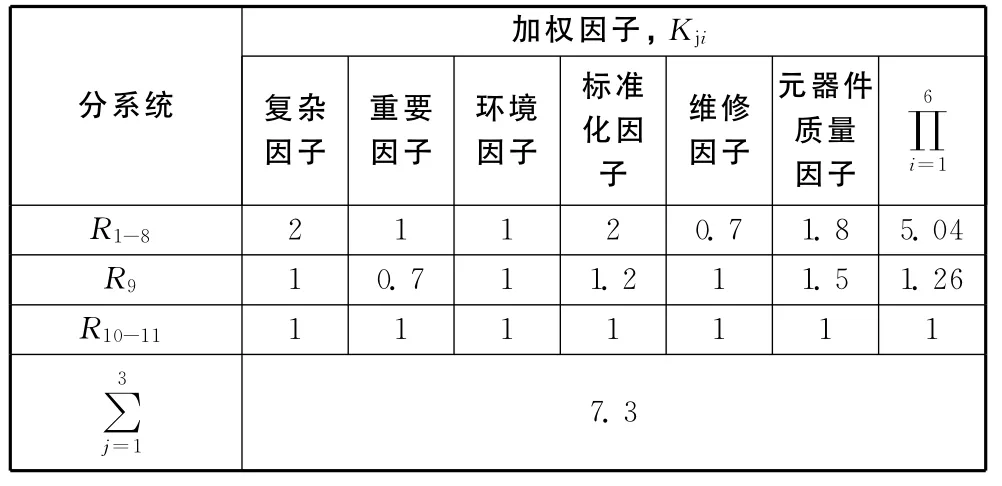
表1 励磁调节器系统各子系统分配加权因子取值表

按加权因子分配法公式［4］：

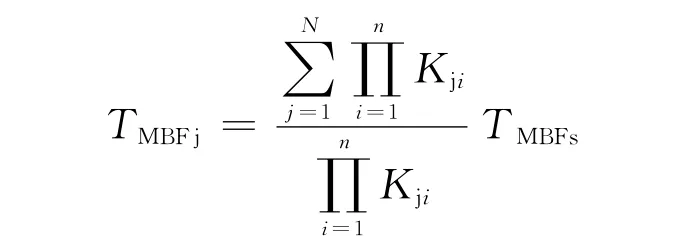
式中：TMBFj为第j个单元平均故障时间间隔；TMTBFs为系统平均故障时间间隔；Kji为第j个单元第i个分配加权因子。

可得到分配结果为：

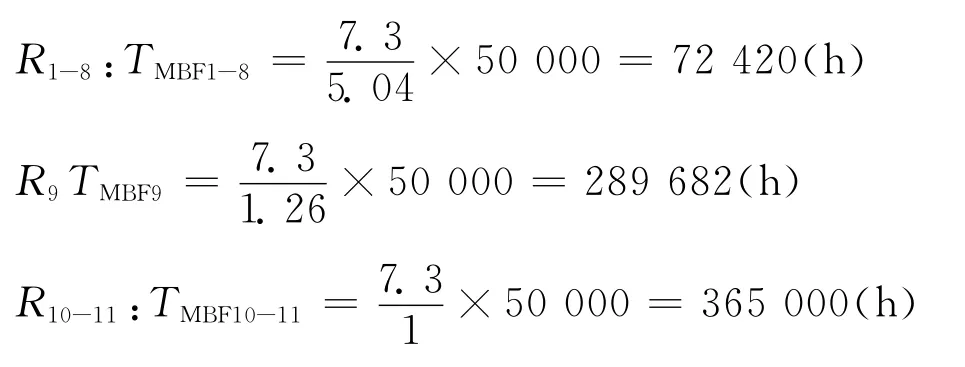
2）R1－4和R5－8的可靠性分配：

R1－8单元由R1－4和R5－8两个单元并联组成，R1－4和R5－8为结构完全相同的冗余关系，所以R1－4＝R5－8，得：R1－8＝2×R1－4－

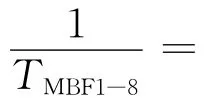
得：λ1－4≈10×λ1－8≈1.38×10－4

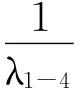
3）R1、R2－3、R4串联及R5、R6－7、R8串联的可靠性分配，各加权因子取值（如表2）。

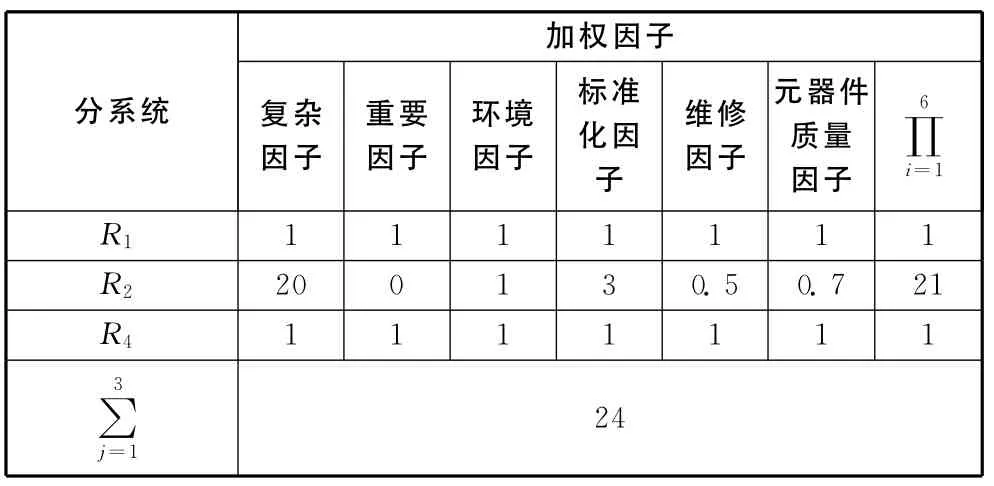
表2 励磁调节器系统各子系统分配加权因子取值表

计算各单元分配的可靠性指标：

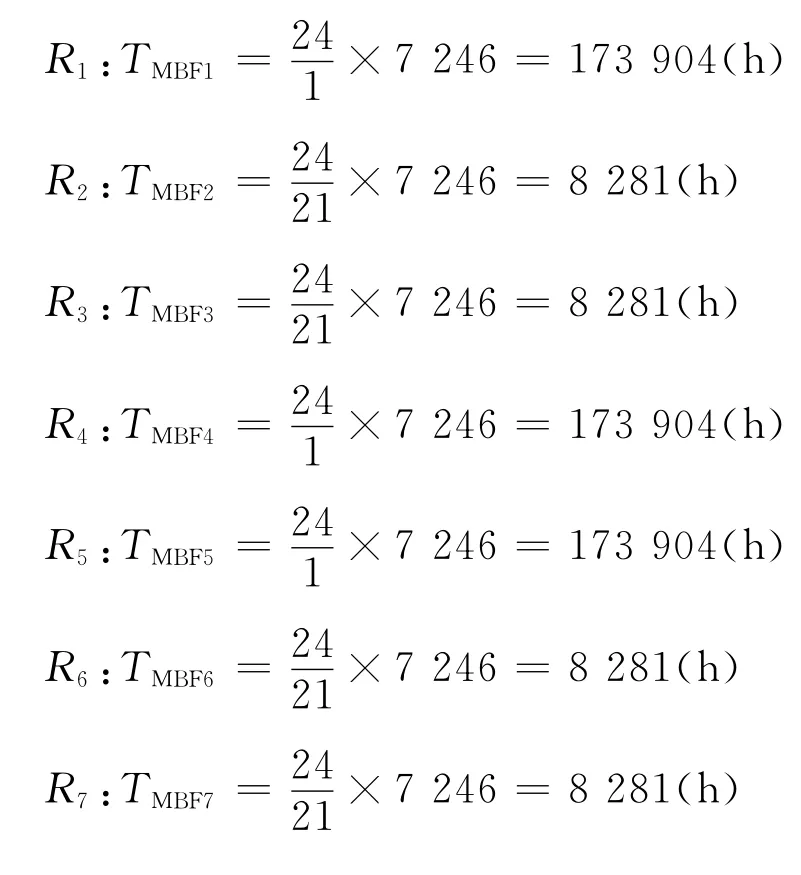
4）和R11的可靠性分配R10和R11为并联冗余结构，同理：

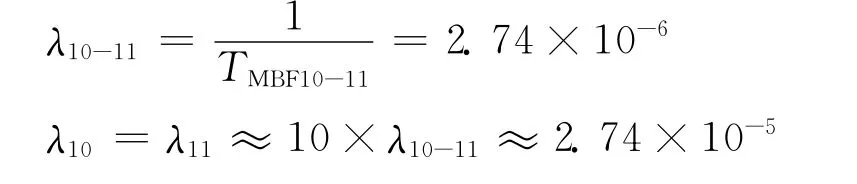
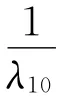
通过以上计算，可得出为满足产品可靠性要求各分系统的平均无故障时间

3 励磁调节器的可靠性预计

可靠性预计是根据系统的可靠性模型、系统的工作环境、系统的结构构成、元器件的质量级别等因素来进行估计，是一个从小到大、由局部到整体、自下而上的一种系统综合过程，它需要，主要用在产品的设计阶段。

由可靠性框图，假设励磁调节器各单元产品均服从指数分布，工作时间均为4 320h，其故障率λ（如表3）。

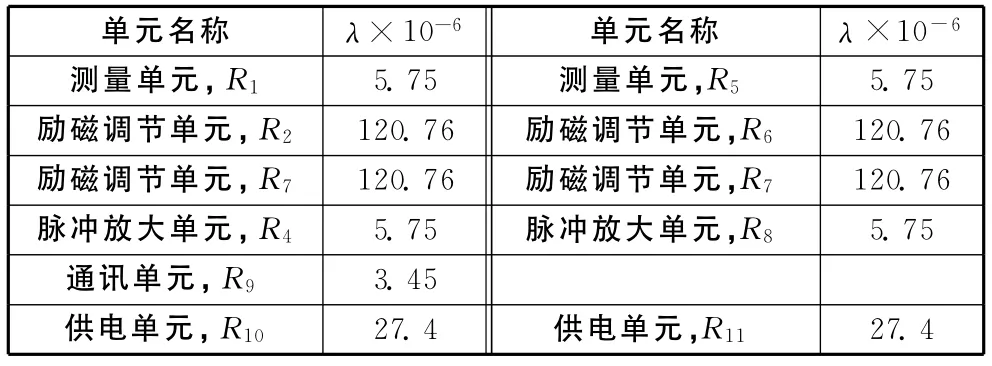
表3 磁调节器各单元故障率λ

其任务可靠度预计如下：

可靠性框图可以化分成三个大的单元。

1）R1、R2－3、R4串联及R5、R6－7、R8串联再并联，其可靠度为：

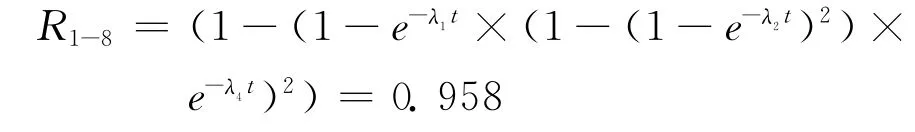
2）R9的可靠度为：

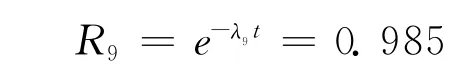
3）R10与R11并联的可靠度：

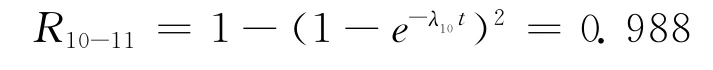
则励磁调节器系统任务可靠度：

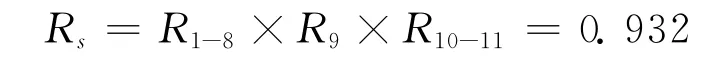
系统Rs大于0.9满足规定的要求。

4 结语

励磁调节器的设计大量采用高可靠性的大规模集成电路芯片替代分立元件，系统中重要的功能组件均采用冗余设计方案，建立了励磁调节器的可靠性模型，简化了硬件电路的设计，有效地进行了励磁调节器的可靠性分配，并通过可靠性预计，系统可靠度满足规定要求。

［1］ 陆继明，毛承雄，范甜等.同步发电机徽机励磁控制［M］.北京：中国电力出版社，2002.

［2］ 赵涌，杨波，王春燕.励磁调节器的可靠性设计［J］.自动化技术与应用，2007（2）：56－57.

［3］ 曾声奎，赵廷弟.系统可靠性设计分析教程［M］.北京：北京航空航天大学出版社，2004.

［4］ 王蓬，王锡吉.可靠性指标工程加权分配法［J］.电子产品可靠性与环境试验，2002（5）：18－21.

［5］ 吕修东，周建平，程志高.于工程加权分配法的某新型火箭炮可靠性分配［J］.四川兵工学报，2010（4）：45－46.