功能联系视角下珠三角扩容的规划探索
赵渺希,周 璇,黎智枫
(1.华南理工大学 建筑学院,广州510640;2.中国城市规划设计研究院,北京100044;3.同济大学建筑与城市规划学院,上海200092)
1 问题的提出
随着全球产业经济重组过程中大都市集聚地带在各国区域经济增长中的地位不断凸现[1-2],城市群已成为中国城镇化进程中吸纳人口和产业的主要空间载体。2013年,国家发改委提出将城市群战略作为区域层面新型城镇化的重要着力点。对既有城市群进行扩容也已经提上了各地新型城镇化的议事日程。2010年有关方面就提出将长三角城市群的核心城市扩容至22个城市,湖南提出将长株潭城市群扩容至8个城市,湖北则提出要将长江中游城市群进行扩容。然而,新型城镇化的城市群战略不能过高地依赖于扩张性财政政策,这在国内业界已经成为共识。由此,要在保证城市群发展品质的基础上进行扩容,合理、有序地吸纳潜在的扩容对象是新型城镇化战略的务实选择。
经过30多年的快速发展,珠三角城市群正向世界级城市群的规划目标迈进。为进一步发挥区域增长引擎的带动作用,扩容也成为当前广东新型城镇化战略的重要内容,这一现实问题正是本研究的出发点。
2 研究方法
2.1 相关理论
关于城市群的扩容并没有直接的理论支撑,但是国内外学术界对于城市群的特征描述和范围界定已经有相对丰富的成果。J.Gottmann阐述了城市群的基本特征和功能界定[3],之后,传统的形态属性分析(城市人口或者产业的规模、密度分布)得到了广泛的应用。而近年来兴起的功能联系分析(城市间的通勤、产业、电话、互联网联系)也正成为当前城市研究的热点,M.Burger等指出,多中心型的全球城市区域内部功能联系的均衡性比形态属性的均衡性更加重要[4]。从功能联系的角度来探讨城市群扩容的区域范围,需要逐次深入地关注空间网络的若干特征。
首先,功能联系的绝对强度是界定城市群的重要依据。近10年来,西方关于城市区域的研究重点已从传统的属性研究转向了关系研究,功能联系成为考察巨型城市区域的重要指标。P.Hall等以生产性服务业网络、通勤流为观察对象,对欧洲8个城市区域的功能联系进行了深入剖析[5]。在国内,根据江曼琦的文献梳理,虽然城市群的界定并没有严格的标准,但是关联网络是其重要的特征之一[6],这一观点得到了大多数学者的认同[7-10]。由此看来,城市群的扩容对象必须有较强的外部网络联系,否则不构成纳入城市群的基准条件。
其次,功能联系的指向分布是界定城市群范围的另一个指标。现实世界中,城市的联系可能会指向周围的任何相邻城市,在这种情况下,可依据其最明显的联系方向确定目标城市隶属于哪一个城市群或者区域范围,这与单个城市的腹地范围划分在原理上是一致的。在应用性的研究中,H.L.Green用人流、物流等6个指标划分纽约和波士顿的影响边界[11]。国内学者对长三角等地的腹地划分实际上也是运用联系指向的比例判别方法[12-14]。对于本研究而言,潜在扩容对象不但应与已有城市群有绝对的功能联系,并且在相对比例上与城市群的联系也应占尽可能大的份额。
第三,城市群内部网络应以多向联系为主,而非指向单一的中心城市,这也是关于均衡型城市区域功能联系的重要观点[15-17]。J.B.Parr指出,网络化的城市区域其空间组织更为均衡[18];D.F.Batten也认为,传统的中心地系统更加强调空间组织的向心性,强调自上而下的单向垂直联系,而更为高级的网络化模式则强调水平联系和中心之间的多向联系[19]。这意味着,从发展的角度来看,扩容城市与珠三角的联系不应过于指向单一的中心城市,而应与多个城市形成密切的联系。
在以功能联系判别城市群的扩容选择时,还应强调潜在扩容对象与珠三角区域的空间邻近性,这是城市群扩容分析的另一个基准前提。N.Green在研究城市区域的多中心形态基础时就专门提出了空间邻近性指标[20]。为此,本研究试图在多类型功能联系分析的基础上,结合空间邻近性来分析珠三角城市群扩容的区域范围。
2.2 计算方法
功能联系包括客运交通、生产性服务业、固定电话通讯、互联网博客4类。其中,客运交通、固定电话通讯都可以通过直接获取的数据进行度量,而对于生产性服务业、互联网博客形成的城市网络,可采用社会网络的方法统计城市之间的功能联系。
在社会网络的分析中,以俱乐部f表示节点i与节点j的基本连接关系,只有2个节点i,j同时在该俱乐部f中,i和j才具有联系。按照二模网络的基本算法[21-23],计Ci,f,Cj,f分别为节点 i,j在俱乐部 f中的价值,节点 i,j之间的联系(Wij)则可以表示为:
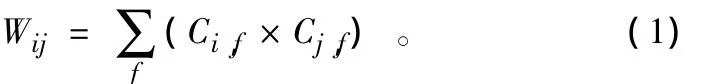
结合上述公式,以生产性服务业的企业区位信息、互联网名人博客的好友地址信息进行社会网络的二模网络建构,实现城市之间联系值的计算。其中,生产性服务业的城市网络研究方法在国内外已经广泛应用[21],而根据社会网络的基本原理,互联网博客网络也具有明显的二模网络特征。
2.2.1 绝对联系强度。联系强度是复杂网络视角下研究城市网络、衡量城市在区域网络中的重要程度的基本指标。在网络中与i具有连接关系的总和即城市i的联系强度,先考虑简单情形即城市联系仅定义为有、无2种的无权网络时,i,j的联系大于0时则计,否则为0。由此,无权网络中节点强度为
在现实的网络中,权重网络更为普遍。假设每类网络中最大联系值为1,定义wij为城市i与j之间功能联系Wij与该类联系最大值的比值,取值范围为0~1,则权重型城市网络中城市i的联系强度(si)为:

参考 P.J.Taylor等[24],B.Derudder等[25]对英格兰、中国城市体系的网络研究,城市联系的总和强度可分离出指向特定城市的强度。对于珠三角外围潜在的扩容城市,可以将联系强度拆分为:① 与珠三角既有的9个城市之间的绝对联系强度(sip);②与广东地区其余11个非珠三角城市之间的联系强度(sinp),并有下述关系:

2.2.2 相对联系强度。对于珠三角潜在的扩容对象,不仅要求该城市有绝对值较高的珠三角联系强度(sip),而且还要求该值尽可能高于与非珠三角城市之间的联系(sinp)。若城市i,j具有相等的绝对联系强度,而二者指向特定区域的联系比重不一致,则与该区域的相对联系强度成为i,j指向归属的区分条件。为此,定义潜在扩容对象指向珠三角城市群的相对联系强度(ri)为:

其中,ri的取值范围为0~1,该值越大说明城市i越趋向于与珠三角城市群发生联系,这也是影响城市群扩容优先的另一项必要条件。
2.2.3 群集性。对于城市群空间网络的多向性特征,可以采用群集性的指标进行度量。向心型指向的城市群不符合多中心的空间组织形式[4,15-17],但是前述公式计算得到的功能联系无论是绝对值还是相对值,其在城市之间的加和仍有可能无法满足城市群内部的多向联系。按照拓扑学的相关理论,以任意3个节点之间的联系组成的三角形数量能表征网络联系的真实状态,即复杂网络统计工具中的群集性指标。D.Watts等提出群集性以衡量网络联系中相邻节点之间的凝聚力,在拓扑学上通过计算三角形的数量来进行统计[26]。假定城市联系为两两相等的无权网络,其计算公式为:

式中:Ei是包含了节点i的三角形数量;ci为群集性,其取值范围为0~1,值越大说明该节点与整个网络中其他节点的三元数组越明显,在网络中的联系也就越紧密;ki是节点的连线数量,ki(ki-1)表示包括城市i在内的组成三角形关系的城市数量。应用到珠三角城市群的扩容选择中,则要求扩容对象要与既有城市群中尽可能多的城市组合形成三元数组形式的功能联系。
对于城市间联系值不尽相等的权重网络,借鉴J.P.Onnela 等[27]的研究,将公式(5)修正为:
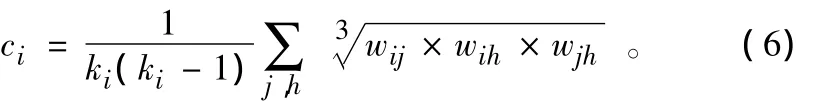
式中:ki(ki-1)表示包括城市i在内的组成三角形关系的城市数量;wij,wih,wjh是联系权重经过标准值化的连边;ci取值范围为0~1,值越大说明扩容对象与城市群中多个城市之间的联系也就越频密。需要指出的是,三元数组中联系权重的大小也与联系的均衡性密切相关(图1)。图1a,1b显然没有形成三元联系数组,故群集性ci为0。由图1c,1d来考察权重联系差异,可以看出,尽管城市i与另外2个城市之间的联系总值都为6,但是图1d的3条边相等因而计算的群集性为1.00,图1c计算的群集性为0.49。显然,图1d所示的城市联系更加接近于巨型城市区域中联系的均衡性特征[4,15-17]。

图1 3个节点联系群集性为0,0~1,1时网络拓扑关系Fig.1 The clustering coefficients of links among three nodes in different situation
2.2.4 扩容优先度。基于绝对联系强度(sip)、相对联系强度(ri)、群集性(ci),对3项指标进行逐一分析后,尝试采用综合性的统计来确定珠三角城市群扩容的优先度。由于量纲的差异,先将各项指标进行标准化处理,即将潜在扩容对象的分项变量分别除以相应变量的最大值,并将其转化为百分制,得到标准化的绝对联系强度(s'ip)、相对联系强度(r'i)、群集性(c'i)。
对分项指标进行综合加权计算有多种方法,如算术平均值、几何平均值等方法,考虑到本研究中的群集性指标、相对联系强度变量在数学公式中是乘积、商的形式,因此,采用几何平均值的方法对分项变量进行综合计算,以保证数学逻辑的前后连贯,由此,城市群扩容的专项优先度(Fi)为:
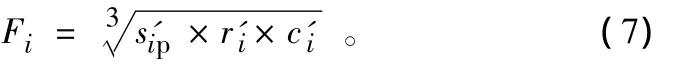
进一步地,考虑到城市功能联系的类型多样化特征,还有必要对各种不同类型专项优先度进行综合评价,定义Fi,k为第k类型联系中城市i的优先度,同样采用几何平均值的方法得到联系优先度(Pi)为:

最后基于多中心城市区域中空间距离的重要性,计算潜在扩容对象与珠三角城市群几何中心的空间距离,对距离取倒数后进行标准值化,得到邻近性得分(Ni),之后取其与联系优先度的几何平均值,从而得到潜在对象的综合扩容优先度(Si)分值:

2.3 研究对象
2013年广东省住房与建设厅委托10余家科研院所进行新型城镇化的研究,依据空间邻近性的原则预先确定了珠三角周边区域的阳江、云浮、清远、河源、汕尾5个地级城市为近期考察的扩容对象,由此确定了本研究的主要对象。
通过比较2000,2010年人口普查数据以及当年的地区生产总值可以看出,珠三角是广东地区常住人口、经济总量10年间增长最为明显的区域,其中珠江口东岸的深圳、惠州最为突出,而珠江西岸江门、肇庆的增长相对较缓;周边区域中清远、河源的增长非常突出,而阳江发展相对较缓,其他区域中,粤西湛江的发展相对稳健,汕头的人口增长明显,但是经济增长乏力,粤北韶关的人口增长最为缓慢(表1)。

表1 2000,2010年广东21个城市基本情况Tab.1 The basic situation of 21 cities in Guangdong Province in the years of 2000 and 2010
2.4 数据来源
网络数据方面,针对客运交通、生产性服务业、固定电话通讯、互联网博客4类数据分别进行收集。
广东地区的省内客运交通主要以陆路为主,2011年全省全社会客运总量中铁路、公路所占比重高达98%,因此,城际客运交通采用城际列车和长途公路陆路客运的总和。由于无法直接对这2种交通方式的班次进行获取,先在中国铁路服务网站上查询非高峰时段余票的方式,获取城际列车班次的实际客运量,再将这一列车客运量折算成40人/车的长途公路客运班次,再与查询到的长途公路客运班次相加,得到2013年广东全省城市之间的客运交通班次。
生产性服务业的联系数据以2010年中国地级以上城市的生产性服务业区位数据为基础,且相关研究成果已经公开发表。在此基础上,于2013年对这一数据库进行了更新和补充,总共有331家银行、保险公司、证券公司、律师事务所、咨询管理与设计公司、广告公司,采用Taylor的连锁模型进行赋值和计算。
固定电话通讯数据则采用了广东地区2013年5月某通信运营商的城市间固定电话联系,数据来自于中国城市规划设计研究院相关部门。
互联网博客数据来自于国内知名互联网门户网易的名人博客,数据于2010年初次抽样获取,在2013年重新进行了最终整理,选取了中国名人博客排名前100位的博主,并对每位博主的前100名好友进行地址信息的提取,好友数量不足100的则纳入其全部好友的地点信息。在此基础上,按照二模网络的计算方法形成了中国287个城市的联系,在其中抽取广东地区21个地级以上城市的子网络。
3 研究结果
3.1 扩容对象的绝对联系强度
5个扩容对象城市与珠三角区域9个城市之间的联系(图2)表明,清远、河源在客运交通方面有比较大的对外联系值,其中清远与广州之间的交通联系非常突出,而河源与广州、深圳之间的客运相对均衡,其余3个城市与珠三角的客运联系相对较弱;生产性服务业的联系中,5个城市指向珠三角的联系比重基本相似,差异性不大;固定电话联系呈现出一定的差异,其中汕尾与深圳之间的电话联系相对较强;互联网联系方面,清远、河源、汕尾与珠三角的绝对联系较强。
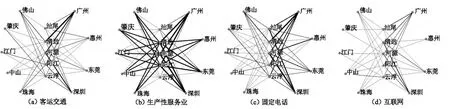
图2 5个扩容对象与珠三角各城市客运交通、生产性服务业、固定电话、互联网的绝对联系Fig.2 Real linkage of passenger transport,productive service,fixed-line telephone and internet between the five potential expansive cities and other cities in Pear River Delta
各个扩容城市与珠三角区域之间总的绝对联系值(sip)表明,河源与珠三角的联系最为频密,稍次为清远,这2个城市构成了联系最密切的扩容对象;阳江次次之,而云浮、汕尾与珠三角区域的联系最弱(图3)。
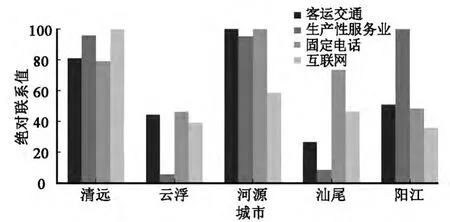
图3 5个扩容对象与珠三角区域客运交通、生产性服务业、固定电话、互联网的绝对联系值Fig.3 Linkage of passenger transport,productive service,fixed-line telephone and internet between the five potential expansive cities and Pear River Delta
从潜在扩容城市的首位/次位指向城市(表2)的行数据可以看出,潜在扩容对象的4类联系中,首位、次位联系的指向城市大多数都包含了广州、深圳,其中,深圳的出现频次(15)比广州的出现频次(19)稍低一些。在各个城市具体的重要联系指向城市中,清远的首位、次位联系中广州、深圳、佛山占据着一定的份量;云浮的重要指向对象则包括广州、肇庆、深圳、中山,但是数据有一定的波动性;河源的外部联系中深圳、广州一直很稳定地分别居于前2位;汕尾的对外联系中深圳、广州、惠州居前;阳江的重要联系对象与河源类似,广州、深圳的地位最为重要。按照联系的类别来看待表2的列数据,客运交通、固定电话的联系中首位、次位城市相对离散,生产性服务业的首位、次位指向城市均为深圳、广州,互联网的联系首位、次位指向城市也全部为广州、深圳。
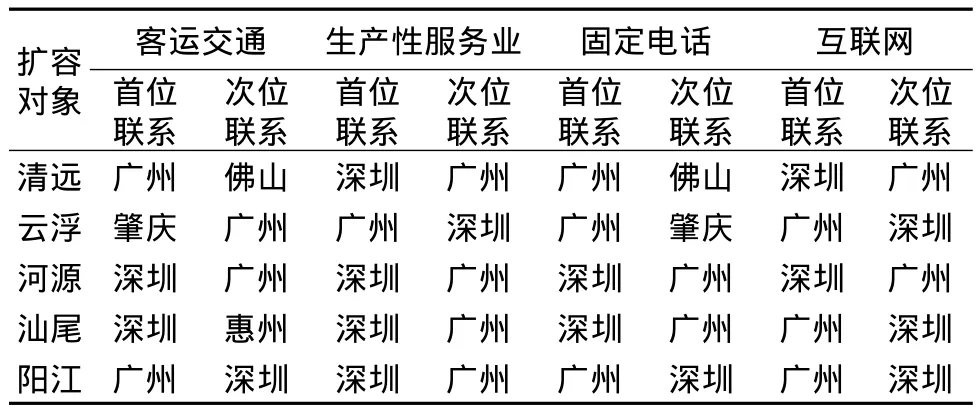
表2 潜在扩容城市的首位/次位指向城市Tab.2 First and second related city of the five potential expansive cities
3.2 扩容对象的相对联系强度
通过图形的直观比较分析潜在扩容城市与珠三角/非珠三角区域的联系分布(ri),可以观察到4类指向珠三角扇面的联系都非常突出,客运交通、互联网博客联系的2个扇面差异比较明显,生产性服务业的指向差异相对较弱(图4)。
将5个扩容对象与珠三角、非珠三角城市的联系进行独立样本的t检验,以p值 <0.05为联系指向的判别标准,通过显著性的项数分析可以发现,4类功能联系中,河源对珠三角城市的指向均有明显的显著性,清远、云浮、阳江各有3类联系具有显著性的珠三角指向,汕尾的显著性指向仅有1项(表3)。
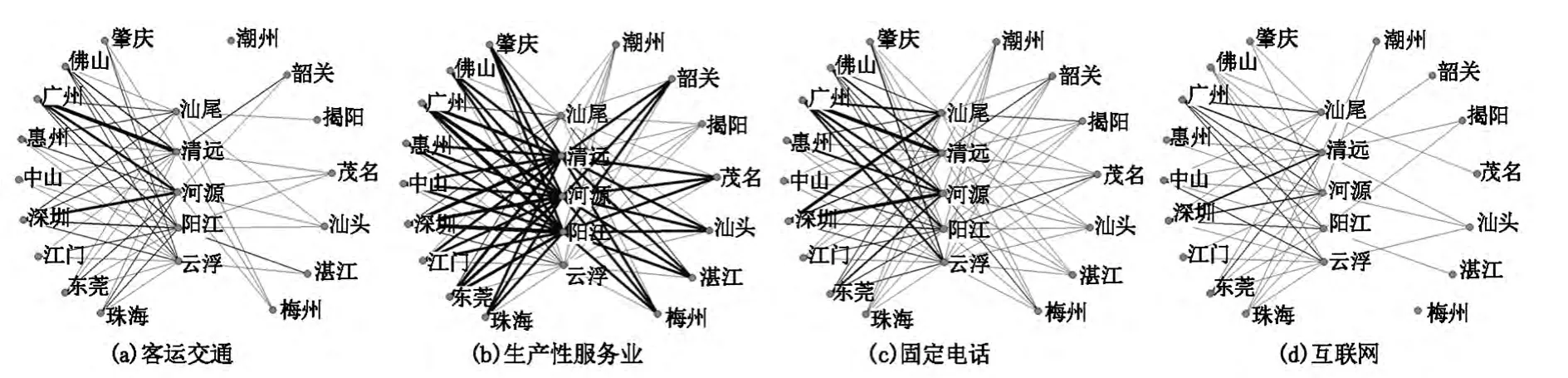
图4 5个扩容对象与广东各地级以上城市客运交通、生产性服务业、固定电话、互联网的绝对联系Fig.4 Real linkage of passenger transport,productive service,fixed-line telephone and internet between the five potential expansive cities and other cities in Guangdong Province

表3 5个扩容对象独立性检验及相对联系强度指标Tab.3 Independent samples test and relative linkage of the five potential expansive cities
进一步计算珠三角区域在各个扩容对象外部联系中的重要程度。相比于绝对联系强度,扩容对象的相对联系强度的差异性都不大,除去生产性服务业的相对联系强度在0.60上下波动以外,其余3项功能联系指向珠三角的比重都在0.85以上,这说明了5个扩容对象强烈地依附于珠三角城市群的影响。
在分项的相对联系强度方面,云浮、河源指向珠三角的客运联系比重较大,汕尾的生产性服务业、互联网联系指向珠三角的比重高于其他城市,但优势并不明显。相对联系强度的区分度不明显主要与这5个城市分别环绕珠三角东、西、北的地理格局有关,也是城市空间邻近的区域形态属性所导致的一种必然结果。
3.3 扩容对象的群集性
4类功能联系的群集性(图5)表明,在客运交通方面河源的该项数值最高(0.059),且显著高于其余4个扩容对象城市。清远、阳江的客运交通融入珠三角的群集性相对较低,甚至低于粤东的汕尾,主要是因为清远在指向珠三角的联系过程中主要与广州发生联系,阳江仅仅指向广州和深圳,而汕尾与广州、深圳、惠州均有相对紧密的联系。在生产性服务业方面,清远、河源、阳江的群集性相对比较接近(分别为 0.070,0.070,0.072),反映了这3个城市在吸引生产性服务业分支机构方面的区位相似性,而另2个城市相对较弱。若以生产性服务业区位作为珠三角建设世界级城市群扩容的衡量基准,显然清远、河源、阳江的优势相对突出。
固定电话联系的群集性相对较为均衡,5个潜在的扩容对象之间的差异性并不大,其中河源较高(0.027),清远、汕尾相对接近。与固定电话类似,互联网联系的群集性总体较低,最高的清远也仅为0.016,且各城市之间的差异性更小。
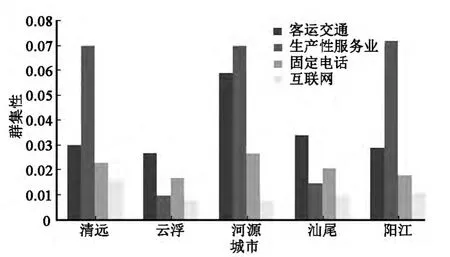
图5 5个扩容对象各项群集性指标比较Fig.5 Passenger transport,productive service,fixed-line telephone and internet comparisons among the five potential expansion cities
3.4 扩容对象的优先度
在上述分项剖析的基础上,以百分制计算各项初始变量的标准化值,并分析不同类型功能联系的分项优先度,再计算出综合联系的优先度,进而结合空间邻近性得到扩容对象的综合优先度(表4)。
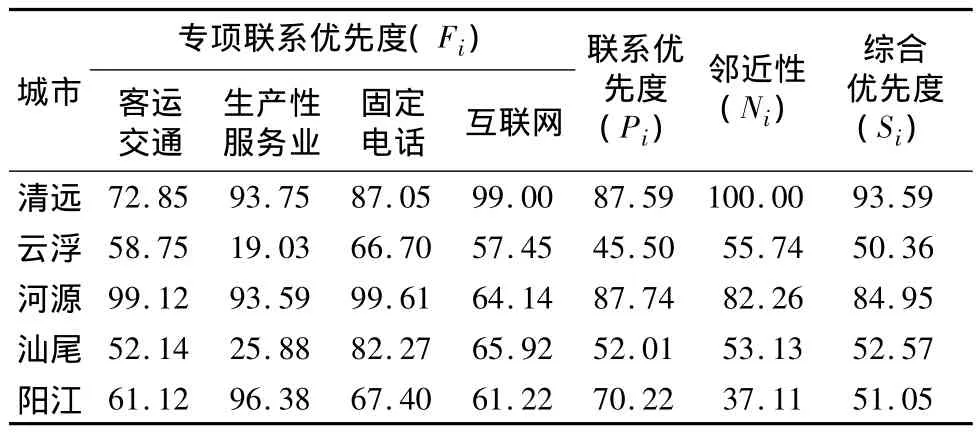
表4 5个扩容对象优先度指标比较Tab.4 Comparison of priority among the five potential expansive cities
首先,考察城市群潜在扩容对象的分项优先度。在客运交通联系方面,河源具有最高的扩容优先度得分,且第2位城市清远与其相差较大,阳江在交通方面的扩容优先度位居第3位;生产性服务业联系方面,清远、河源、阳江的得分较高,而云浮、汕尾则明显偏低;固定电话联系方面,河源较高,清远、汕尾次之,阳江和云浮较低;互联网联系方面,清远得分最高,汕尾、河源、阳江等城市远低于清远,但三者得分差距不大。
其次,比较潜在扩容对象的联系优先度。明显地,清远、河源优先度得分十分接近,分别为87.59,87.74,阳江的优先度得分也较高,为70.22,而云浮、汕尾的联系优先度得分较低。
最后,加入邻近性指标后计算扩容综合优先度。可以看出,清远因为距离珠三角城市群最近而综合优先度最高(93.59),河源略有下降(84.95)但仍处于高位。加入邻近性指标后的综合优先度下降最多的是阳江,尽管该城市的联系优先度非常突出,但是空间距离制约了最终的综合优先度得分,汕尾、云浮变化不大。显然,珠三角周围的5个城市中,清远、河源的扩容条件较为成熟。
4 规划建议与展望
珠三角周围5个城市的扩容条件差异较大,其中粤北的清远和粤东北的河源是目前扩容的首选城市,近期应重点建设这2个条件相对成熟的城市,并将其塑造为带动区域发展的桥头堡。由于清远北部的连南、连山等少数民族山区属于北江流域上游,河源东北部的部分山区县同样环境容量有限,在广东省的主体功能区规划中,清远的连山县、连南县、连州市、阳山县、清新县5个县(市)以及河源的龙川县、连平县、和平县被列入省级重点生态功能区,河源的东源县、紫金县被划入国家级农产品主产区。环保需求和发展腹地受限将是清远和河源纳入扩容区域的主要制约因素。但是清远的清城区、佛冈县和河源的源城区是省级重点开发区域,承担着珠三角及国内外产业转移和形成北部山区服务中心与增长极的职能。因此,珠三角的扩容范围可以依照肇庆的惯例将相对成熟的县(区)划入,即清远的清城区和佛冈县,河源的源城区、紫金县和东源县,其余地区仍旧以生态保育、旅游休闲为主。
展望远期的城市群扩容范围,现状的数据分析不可避免地会遇到趋势外推的制约。但是,从城市群的发育规律来看,珠三角远景的区域范围并不一定要遵循空间邻近的原则同时向周边5个城市摊开,考察这一拓展模式(图6)可以发现,这种模式只不过强化了广东省地区的核心-外围结构。虽然区域基础设施建设相对节省,但是越往外城市发展的动力越弱,这种向心式的发展格局并不利于多中心的培育。而根据本研究,舍弃珠三角向周边五市均匀摊开的扩容思路,依照广东省主体功能区的规划,仅仅纳入清远、河源的主城区,这也体现了区域精明增长的发展理念。
5 结语
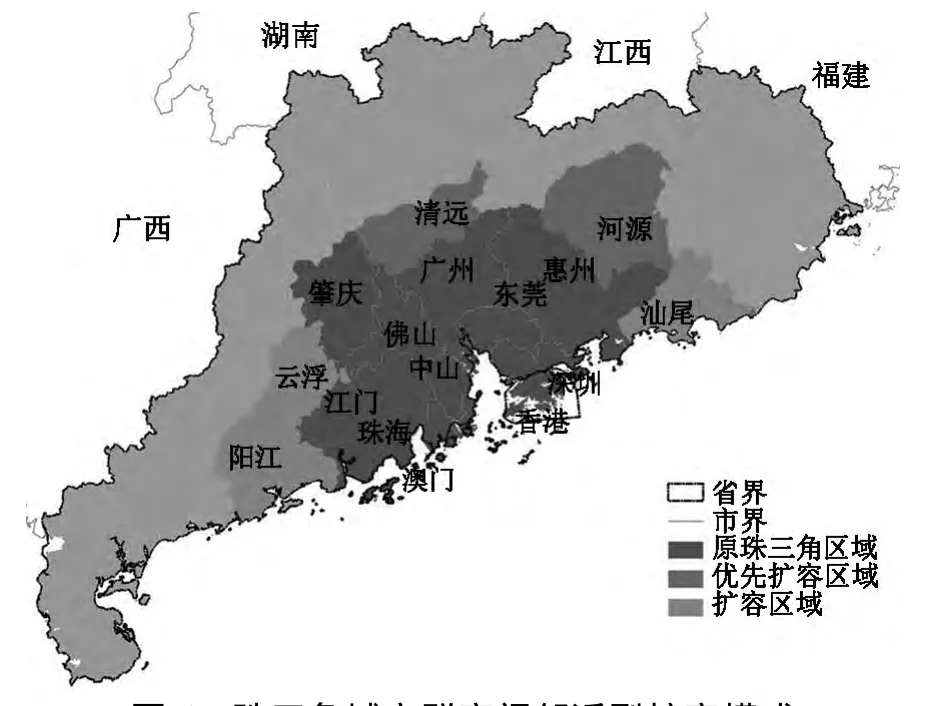
图6 珠三角城市群空间邻近型扩容模式Fig.6 Expansion mode of Pear River Delta region based on spatial proximity
清远和河源与珠三角的紧密联系是客观地理现象,这是由地理邻近效应与城市发展的自身规律所造成的。而扩容的规划便是对这种现象的控制和引导。把条件成熟的县(市,区)划入珠三角区域将延续城市发展规律,但却面临着环保的制约。一方面可以采取财政转移支付的方式,将区域发展的外部性问题内部化,确保粤东北地区的区域生态安全格局;另一方面若清远、河源等中心城区的人口吸纳能力得到提升,强化珠三角经济区外围的反磁力中心建设,对实现多核心网络区域结构有推动作用。若将联系较弱的汕尾或者阳江纳入珠三角区域范围,离珠三角核心区域的广州和东莞的距离增大,区域的发展动力缺乏,有可能造成进一步的资源浪费。
当然,城市群的扩容除要考虑与周边城市功能联系外,还要根据规划的目的和任务对扩容范围进行相应的调整。城市和区域规划作为公共政策本身就具有平衡和妥协的特点,因此,本研究也仅可作为政府决策的依据之一。
[1] Scott A.Global City-Regions:Trends,Theory,Policy[M].New York:Oxford University Press,2001.
[2] Scott A,Storper M.Regions,Globalization,Development[J].Regional Studies,2003,37(6/7):579-593.
[3] Gottmann J.Megalopolis:Or the Urbanization of the Northeastern Seaboard[J].Economic Geography,1957,33(3):189-120.
[4] Burger M,Meijers E.Form Follows Function?Linking Morphological and Functional Polycentricity[J].Urban Studies,2012,49(5):1127-1149.
[5] Hall P,Pain K.The Polycentric Metropolis:Learning from Mega-City Regions in Europe[M].London:Earthscan,2006.
[6] 江曼琦.对城市群及其相关概念的重新认识[J].城市发展研究,2013,20(5):30-35.
[7] 姚士谋,陈振光,朱英明,等.中国城市群[M].合肥:中国科学技术大学出版社,2001.
[8] 顾朝林.城市群研究进展与展望[J].地理研究,2011,30(5):771-784.
[9] 唐子来,赵渺希.经济全球化视角下长三角区域的城市体系演化:关联网络和价值区段的分析方法[J].城市规划学刊,2010(1):29-34.
[10] 罗震东,朱查松.解读多中心:形态、功能与治理[J].国际城市规划,2008,23(1):85-88.
[11] Green H L.Hinterland Boundaries of New York and Boston in Southern New England[J].Economic Geography,1955,31(3):283-300.
[12] 王德,赵锦华.城镇势力圈划分计算机系统HAP的开发研究与应用——兼论势力圈的空间结构特征[J].城市规划,2000,24(12):37-41.
[13] 王德,郭洁.沪宁杭地区城市影响腹地的划分及其动态变化研究[J].城市规划汇刊,2003(6):6-11.
[14] 赵渺希,唐子来.基于企业网络关联的长三角区域腹地划分[J].经济地理,2010,30(3):371-376.
[15] Limtanakool N,Schwanen T,Dijst M.Developments in the Dutch Urban Systems on the Basis of Flows[J].Regional Studies,2009,43(2):179-196.
[16] Meijers E J,Burger M J.Spatial Structure and Productivity in USMetropolitan Areas[J].Environment and Planning A,2010,42(6):1383-1402.
[17] Meijers EJ.Measuring Polycentricity and Its Premises European Planning Studies[J].European Planning Studies,2008,16(9):1313-1323.
[18] Parr JB.The Location of Economic Activity:Central Place Theory and the Wider Urban System[M]//McCann P.Industrial Location Economic.Cheltenham:Edward Elgar Publishing Ltd,2002:32-82.
[19] Batten D F.Network Cities:Creative Urban Agglomerations for the 21st Century[J].Urban Studies,1995,32(2):313-327.
[20] Green N.Functional Polycentricity:A Formal Definition in Terms of Social Network Analysis[J].Urban Studies,2007,44(11):2077-2103.
[21] Taylor P.Specification of the World City Network[J].Geographical Analysis,2001,33(2):181-194.
[22] Neal Z.Structural Determinism in the Interlocking World City Network[J].Geographical Analysis,2012,44(2):162-170.
[23] Liu X,Derudder B.Two-mode Networks and the Interlocking World City Network Model:A Reply to Neal[J].Geographical Analysis,2012,44(2):171-173.
[24] Taylor PJ,Ni P,Derudder B,et al.Global Urban Analysis:A Survey of Cities in Globalization[M].London:Earthscan,2011.
[25] Derudder B,Taylor P J,Hoyler M,et al.Measurement and Interpretation of the Connectivity of Chinese Cities in the World City Network,2010[J].Chinese Geographical Science,2013,23(3):261-273.
[26] Watts D J,Strogatz S H.Collective Dynamics of‘Small-World’Networks[J].Nature,1998,393(6684):440-442.
[27] Onnela J P,Saramaki J,Kertész J,et al.Intensity and Coherence of Motifs in Weighted Complex Networks[J].Physical Review E,2005,71(6):531-536.

