霍金温度的修正对半全息宇宙学模型的影响
郭若毅,陈驰一
(杭州师范大学理学院,浙江 杭州310036)
1933年,弗里茨·兹威基首次发现大星系团中的星系具有极高的运行速度,而要束缚住这些星系,星系团的实际质量应该是通过电磁信号观测到的恒星总质量的100多倍[1].因此,这种无法通过测量其亮度或者电磁效应探测到、和其他普通物质的相互作用也非常微弱的未知物质称为暗物质.星系NGC3198的转动曲线则为暗物质的存在提供了直接的证据[2].之后,Riess等分别利用Ia型超新星作标准烛光,精确测量了距离-红移关系,发现宇宙在加速膨胀[3-5].这一结论的得出是基于标准宇宙学度规,而对其的分析是根据爱因斯坦标准宇宙动力学模型,暗示必须存在一种排斥能(即要求ρ+3p<0),但目前实验室探测到的已知相互作用都不满足这个判据,因此这种能量被命名为暗能量.
暗能量和暗物质是新世纪最重要的两个发现.大多数物理学家都将暗物质和暗能量问题看作是彼此独立的两个问题.对于暗能量问题,物理学家曾试图构建很多物理模型予以解释,如宇宙学常数、Quintessence、phantom、k-essence等[6],然而暗能量的本质是什么却一直没有统一的答案.暗物质问题同样如此.由于这两者发现的时间相距较远,很少有模型提出两者可能存在一定关联性.但是将两者联系在一起考虑也未尝不可,因为暗能量和暗物质问题都是出现在宇观的大尺度上,而在此尺度上起主导作用的相互作用只有引力.况且,暗能量和暗物质还存在所谓巧合性问题(coincidence problem).因此,从自然性的角度分析,暗能量和暗物质问题很可能在物理的深层次本质上是相联系的.
半全息宇宙学模型主要通过熵将暗物质和暗能量联系在一起来研究两者的性质.本文将进一步改进和完善当前关于半全息宇宙学的讨论.Zhang等[7]给出的霍金温度T采用了标度因子变化的平坦性近似,在当前已经发现宇宙存在明显加速膨胀的前提下,这种近似是应该得到修正的.Cai等[8]则给出了明确的修正,得到了霍金温度更准确的表达式.本文正是考虑霍金温度的物理修正以后,重新考察了暗能量和暗物质通过熵结合的半全息宇宙学模型,着重处理了巧合性问题,并根据得到的吸引子解来分析讨论宇宙减速因子以及暗物质、暗能量的等效压强密度比.
1 霍金温度T 的修正
为了使半全息宇宙学模型应用更为严谨准确,本文考虑采用霍金温度T的一般表达式来求解半全息宇宙学模型的参数.在这里标准模型的基本假设(宇宙学原理)依然成立,即每一时刻的宇宙物质分布在大尺度下是均匀且各向同性的.根据宇宙学原理,已知n+1维的FRW 宇宙学度规为:
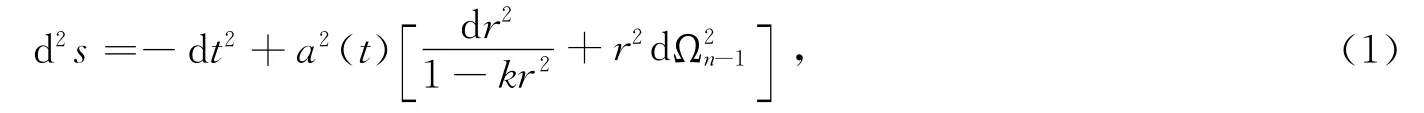
其中a(t)为标度因子,k为空间曲率.上式同样可以等价地表示为:

对于三维的宇宙来说,在其膨胀时期不存在事件视界,但其表观视界却一直存在,所以本文选取表观视界作为暗能量的全息面,根据视界的概念要求:

其中
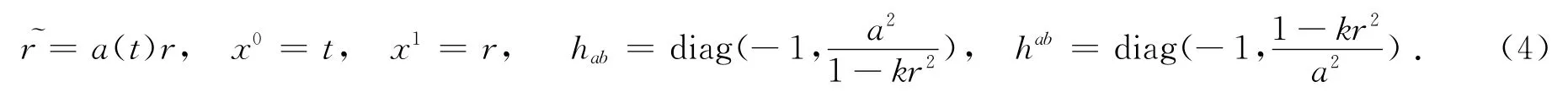
而式(3)可以按具体指标展开为:

结合式(4)即可得表观视界半径为:

其中表示a对时间求一阶导数,下面类似符号也作同样规定.定义表观视界面的表面引力[8]为:



而H对标度因子a求一阶导数为:

其中H′表示H对于lna求偏导数,下面类似符号也作同样规定.所以根据式(2)至(10)以及的条件,表观视界面的引力可以表述为:

在一般情况下,视界因霍金辐射而产生的霍金温度的一般形式[8]为,根据式(11),则在表观视界下的温度T具体表示为根据观测的最佳拟合结果,本文同样研究平坦的宇宙,即k=0,此时,所以有
相比于未修正的霍金温度项,在考虑了标度因子a的二阶导数项的动力学效应后,得到的新的霍金温度项T多出了一个H的一阶导数项.其影响主要表现在暗能量和暗物质的能量密度的演化方程以及吸引子解的结果,可以通过宇宙减速因子及暗能量和暗物质的等效压强密度比加以验证.
2 吸引子解
根据宇宙的演化规律,暗物质和暗能量的密度在当前阶段处在同一量级,但通常情况下,两者随宇宙标度因子的演化规律会呈指数的不同,而宇宙的标度因子在宇宙的整个演化历史中膨胀了很多倍,因此,宇宙早期暗能量与暗物质的能量密度相差极大.为了在宇宙演化的当前时期得到两者处于相当的结果,需要在接近宇宙诞生的时候就对各种物质的比例做非常细致的调整,这种调整的机制以及暗能量本身的性质都让人非常困惑,这也是巧合性问题的由来.对于巧合性问题,如果要得到机制性的解决,则可以采用让暗能量和暗物质的能量密度满足吸引子解的方案来缓解,因为此时暗能量和暗物质的比例只与其状态参数有关.半全息宇宙学模型正是这样一个可以解决巧合性问题的模型,其稳定点处的暗能量和暗物质的比例也正好只与状态参数成比例.它主要通过熵将暗能量和暗物质联系起来,对其进行动力学分析得到哈勃参数的演变方程.在热力学分析的过程中,可以将暗能量和暗物质组成的系统看作是一个封闭的系统,假定其不与外界发生物质交换,应用热力学第一定律讨论暗能量和暗物质的内能变化,得到暗能量或暗物质的能量密度的演化方程.对其求吸引子解,并给出吸引子解的限制条件.
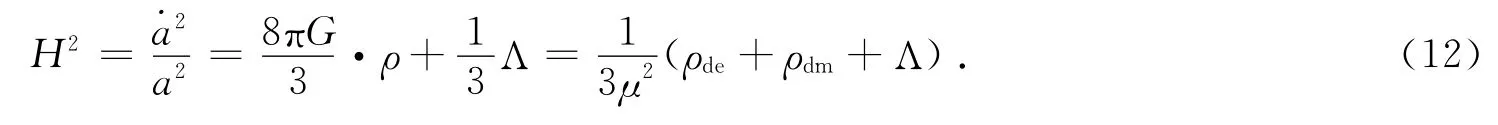
上式两边都对标度因子a求导数,并化简得综合上述两式得H′2=
对暗能量和暗物质分别应用热力学第一定律,得到

应用能-动量张量的守恒律,计算得到暗能量和暗物质的能量密度的演化方程分别为:

同时,式(15)和(16)又称为宇宙动力学方程.为了使暗物质和暗能量的能量密度演化方程形式更简洁,可以定义新变量则式(15)、(16)改写为:
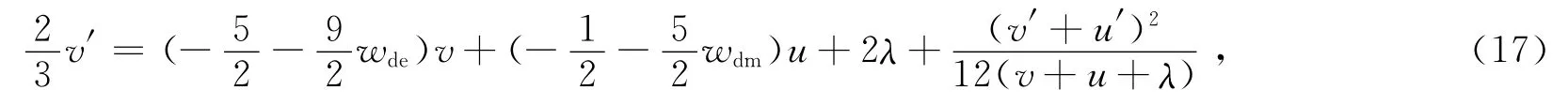

所谓吸引子解,必须是不动点,且要求其具有稳定性.而对于巧合性问题,最简单的情况就是宇宙学参数u、v都满足吸引子解.令u′c=0,v′c=0,代入式(17)和(18),解得临界点为:
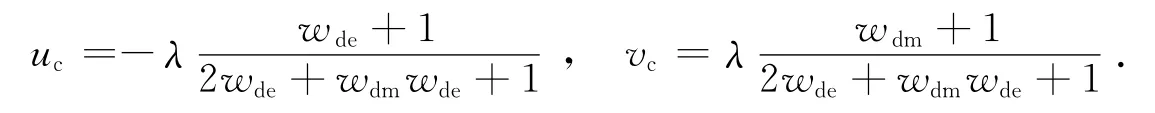
如果宇宙学常数λ≠0,则最终暗物质和暗能量的比例为该式说明临界点处暗物质和暗能量的能量密度的比例只与状态参数有关,这很自然地解释了两者比例的巧合性问题.而对于临界点稳定性问题的研究,可以通过考察宇宙动力学方程相对临界点的偏离度的演化情况来实现.改写u和v为:

那么含有偏离度的暗物质和暗能量的演化方程为:

根据临界点的条件,化简得到偏离度所满足的方程为:
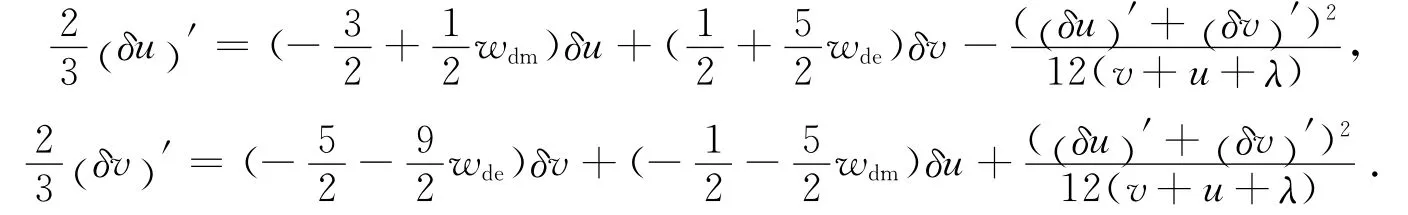
假定暗能量和暗物质的能量密度参数在吸引子解附近都为常数,可以把偏离度作傅里叶展开,即δρ∝ela,则暗能量和暗物质密度参数的偏离度展开式中,最主要的项为一阶偏导数,满足(δρ)′=lδρ.而偏离度作为一阶小量,其平方项可以忽略,那么偏离度的演化方程可以写作矩阵方程组:


如果临界点为稳定的不动点,则要求根必须小于零.只有这时得到的临界点才是吸引子解,即要求1+wdewdm+2wde>0,且实际观测中暗物质和暗能量的状态参数满足,所以得到吸引子解的限制条件为根据这一限制条件,本文选取wde=-0.62,wdm=-0.42.下文通过宇宙减速因子以及暗能量和暗物质的等效压强密度比来检验这一模型修正前后的变化.
3 应用
3.1 宇宙减速因子
宇宙减速因子是宇宙观测最重要的参数,用来描述宇宙膨胀的加速度情况.其定义式为当q>0时,宇宙在减速膨胀;反之,宇宙在加速膨胀.根据H的变换形式,减速因子可以化简为
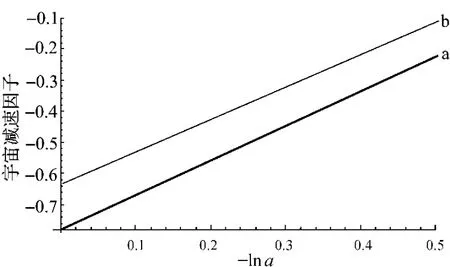
图1 半全息宇宙学模型和宇宙学常数模型中宇宙减速因子q的演化曲线Fig.1 The evolutions of qin semi-holographic universe andΛCDM
根据半全息宇宙学模型[7],本文选取横轴为-lna来研究宇宙减速因子q随宇宙红移的变化规律,并取现今宇宙的参数初值为u0=0.25,v0=0.01,λ=0.74.q随-lna的变化如图1所示.可见两曲线的变化趋势基本一致,q在图中所示的区段内取负值,意味着宇宙此时处于加速膨胀;而在当前时刻q的取值是不同的,对于半全息宇宙学模型,对应值约为-0.74.
3.2 等效压强密度比
当考虑暗能量或暗物质对宇宙演化的影响时,压强必须为等效压强,其定义式为0.它是由能量密度随宇宙膨胀的演化行为所决定的,可化简为等效密度压强比为所以,求得暗物质和暗能量的等效压强密度比的解析表达式分别为:

根据式(19)和(20),图2描绘出了暗能量和暗物质的等效压强密度比随-lna的变化情况(选取的参数初值和讨论减速因子时相同).相比半全息宇宙学模型给出的演化图,在图2中可以发现类似的规律:当宇宙处于较大红移时,暗物质的等效压强密度比逐渐趋近于零,这意味着此时暗物质转变为重子物质;对于暗能量,随着红移逐渐增大,其等效压强密度比经历着从phantom 模型到宇宙学常数模型的变化,最后接近-1,刚好就是宇宙学常数模型的结果.但标度因子a的二阶导数产生的动力学效应使得图2具体的变化趋势与前者有所不同:暗物质在红移小于原先位置时就转变为了重子物质;暗能量的等效压强密度比取最大值时的位置和大小较霍金温度修正前发生了变化.
4 结束语
霍金温度T是在求解吸引子问题中比较重要的一个参数项,考虑到标度因子a的二阶导数存在缓慢变化的动力学效应,本文对霍金温度T进行了修正,并将修正后的霍金温度T重新应用于半全息宇宙学模型的讨论.文章在熵守恒的前提下重点讨论了暗能量和暗物质的巧合性问题,发现满足吸引子解时暗能量和暗物质的比例只与它们的状态参数有关,由此解释了巧合性问题,同时也给出了吸引子解的限制条件.依据得到的吸引子解,讨论了宇宙学观测的两项重要指标宇宙减速因子和等效压强密度比.结果发现修正后的半全息宇宙学模型中宇宙减速因子随-lna的变化规律与ΛCDM 模型接近,且减速因子取负值也很好符合了宇宙在加速膨胀这一事实,但是其在当前时刻对于减速因子给出了不同的预测值;相比之前的半全息宇宙学模型,当宇宙处于较大红移处时,暗物质的等效压强密度比逐渐趋向于零,反之重子物质则随着宇宙演化向暗物质转变;随着宇宙红移逐渐增大,暗能量经历着由Phantom 模型向宇宙学常数模型的转变,直至最后其等效压强密度比趋向于-1,此时正是宇宙学常数对应的状态参数值.标度因子的二阶导数产生的动力学效应使得暗物质在红移小于原先位置时就转变为了重子物质,而暗能量的等效压强密度比与修正之前的差别主要在于最高点处的数值和位置不同.
[1]Zwicky F.Die Rotverschiebung von extragalaktischen Nebeln[J].Helvetica Physica Acta,1933,6:110-127.
[2]Begeman K G,Broeils A H,Sanders R H.Extended rotation curves of spiral galaxies:dark haloes and modified dynamics[J].Monthly Notices of the Royal Astronomical Society,1991,249(3):523-537.
[3]Riess A G,Filippenko A V,Challis P,etal.Observational evidence from supernovae for an accelerating universe and a cosmological constant[J].The Astronomical Journal,1998,116(3):1009-1038.
[4]Perlmutter S,Aldering G,Goldhaber G,etal.Measurements ofΩandΛfrom 42high-redshift supernovae[J].The Astrophysical Journal,1999,517(2):565-586.
[5]Hinshaw G,Larson D,Komatsu E,etal.Nine-year wilkinson microwave anisotropy probe(WMAP)observations:cosmological parameter results[J].The Astrophysical Journal Supplement Series,2013,208(2):19-43.
[6]Bamba K,Capozziello S,Nojiri S,etal.Dark energy cosmology:the equivalent description via different theoretical models and cosmography tests[J].Astrophysics and Space Science,2012,342(1):155-228.
[7]Zhang H S,Li X Z,Noh H.Semi-holographic universe[J].Physics Letters B,2010,694(3):177-180.
[8]Cai R G,Kim S P.First law of thermodynamics and Friedmann equations of Friedmann-Robertson-Walker universe[J].Journal of High Energy Physics,2005(2):1-14.

