排土机排料臂频率分析
孙 刚, 李爱峰
(太原重型机械集团,山西 太原 030024)
排土机是露天矿用半连续开采或连续开采成套装备之一,通过与破碎站配合作用,完成物料的排弃。排土机的排料臂因工艺要求,结构采用钢丝绳悬挂结构,排料臂上设置有一条带式输送机,两侧有走台,长度一般50~60m之间,其结构示意图见图1。
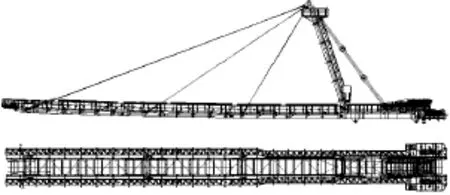
图1 排料皮带机结构简图
对于这种结构的带式输送机,为防止物料因震动引起的抛洒,有必要对其结构进行频率分析,防止产生共振。第一、需要考虑托辊和输送带是否有较大的震动,第二、需考虑作为激励源的输送机,是否会引起钢结构的较大震动。
1 托辊和输送带的频率分析
1.1 托辊振动判断
正常的直线段托辊间距简称托辊间距,影响托辊间距的主要因素:输送带在托辊间的垂度和带速、辊子轴承和辊子轴的承载能力,避开托辊的振动频率与输送带的固有频率接近而产生共振。
在两组托辊支撑之间由于输送带和物料重力的作用输送带要发生下垂,假设输送带是挠性体,并认为载荷均匀分布。如图2所示输送带在A,B两处支撑下输送带的挠曲曲线为AKB。

图2 输送机挠度简图
设输送带的张力在AB区段不变,取AK段为隔离体,A点输送带的张力TA分解为T和TV,由于输送带在任意截面上不受弯矩,作用在K截面上的力矩等于0。即:

所以可以求出最大悬垂度:
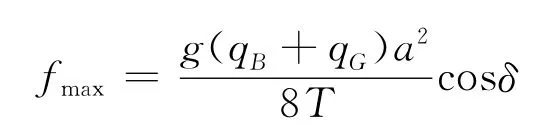
式中,T为输送带张力;a为托辊间距;qB为单位长度输送带质量;qq为单位长度物料的质量;δ为托辊与水平线夹角。
避免共振的问题是托辊作为振动的振源提供强迫振动,其振动频率取决于托辊的转速,在托辊支撑之间,输送带作上下横向振动的固有频率应避免接近强迫共振的频率。横向振动的固有频率可以将输送带简化成弦,设横向振动的位移为u,忽略输送带和物料的重力作用,考虑一个微单元如图3所示。

图3 微单元的受力图
微单元上的受力在u方向上平衡,可以受力平衡得:
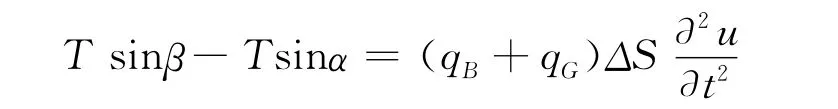
而ΔS→0,即

可以得到

此方程为一阶波动方程,得到

式中:d为个托辊半径。
带式输送机的最大张力T=20t=200 000N.
在7 000~9 000t/h运量下,可能发生共振的托辊间距如表1,太原重型机械集团设计的产品托辊间距为1m。因此,不会发生共振。

表1 发生共振的托辊间距
1.2 输送带振动判断
钢丝绳芯输送带的带芯是钢丝绳,钢丝绳的直径与输送带的厚度相比较小,需计入橡胶的影响。

式中,橡胶的弹性模量Er=7.8×106Pa;橡胶的泊松比υ=0.47;钢丝绳的弹性模量Ea=1011Pa;钢丝绳对中轴的惯性矩J=10 523 d4ε;钢丝绳的直径dε=6×10-3m;钢丝绳的间距t0=12×10-3m;输送带芯的厚度h′=6×10-3m。
如图4所示,假设槽形带的各平面的交线(图中虚线)在横截面上不运动,因而可以将此线看成两个平板的固定边界(C);输送带的边缘没有约束,是自由边界(F);托辊支撑处没有位移,不受弯矩的作用,可以看成是铰接边界(S)。这样,将槽形输送带的边界条件归结为SCSC的边界条件。

图4 槽形输送带的边界条件

式中:a为托辊间距;b托辊长度。故,输送带应力:

两边固定的边界条件可以得到方程

所一阶固有频率,即m=1,带入相应的数值得到方程:

在求解δ,σ时需要采用数值求解方程的方法进行,采用最小二乘法解决此非线性方程组,最后收敛于σ=2.38,δ=0。
可以得到无量纲的中间值

最终带入振动的固有频率为

针对不同的输送量可以得到不同的振动频率如表2。

表2 输送机的输送量与振动频率
2 主钢结构的震动分析
2.1 模型简化
根据排土机工作状况及臂架结构特点,臂架结构有限元模型主要由梁单元与实体单元组成。臂架液压缸处施加固定约束,限制三个方向的自由度。输送带、辊子及其上物料、走台以均布载荷的形式施加于梁单元的节点上。钢丝绳由等效刚度的弹簧接头代替。
2.2 有限元模型处理
梁单元与实体单元采用刚性连接方法,考虑臂架连接处转动,采用销轴连接。
2.3 结果分析(见图5和表3)

图5 第一~第五阶振型图

表3 第一~第五阶自振频率
3 结论
1)参照托辊的振动计算,可以知道,输送机正常运行时,托辊不会发生共振。
2)作为激励源的输送机,其不同的输送量条件下,其振动频率分别为7.44Hz、6.95Hz和6.67Hz。由有限元计算结果可知,臂架系统的基频为1.356Hz,远低于激励源的频率,因此,结构不会发生共振。
综上所述,排料臂架不会发生共振。
[1] 宋伟刚,邓永胜,刘兴文.带式输送机避免共振设计的研究.东北大学学报(自然科学版).2002,23(3):281-284.
[2] 胡吉全,赵章焰.起重机臂架结构模态分析.中国机械工程学报.2004,10,2(4):441-443.

