混凝土弹塑性损伤本构模型参数及其工程应用

齐 虎，李云贵，吕西林

（1.中国建筑股份有限公司技术中心，北京101320；2.同济大学 结构工程与防灾研究所，上海200092）

弹塑性损伤本构模型能够准确地模拟混凝土非线性本构行为［1-4］.目前，学者们提出了多个理论完备、计算准确度高的混凝土弹塑性本构模型［5-7］，但是多数模型的数值处理复杂，计算过程涉及多次迭代，计算效率较低、数值稳定性不好，且模型中涉及的参数较多，参数的标定是一项繁琐的工作，因此这些模型较难应用于实际工程.齐虎等［8］提出了一个计算效率高、数值稳定性好的实用弹塑性损伤本构模型，但仍然存在参数较多，实际应用困难的问题.本文对弹塑性损伤本构模型［8］中各参数取值进行系统研究，并研究各个参数对模型计算本构曲线的影响.通过比较计算结果与试验结果，给出模型参数与混凝土材料单轴抗拉强度、抗压强度和弹性模量的函数关系.从而在使用中只须给定材料抗拉强度、抗压强度和弹性模量就能方便地确定模型的参数取值，提高模型的实用性.

将齐虎等［8］开发的弹塑性损伤本构模型在ABAQUS中进行二次开发，并采用本文提出的方法确定模型参数取值，对上海浦东香格里拉酒店进行数值模拟.上海浦东香格里拉酒店是由一栋41层、总高度为152.8 m的塔楼和4层裙房组成的超高层框架——剪力墙结构，结构高度超限且平面布置不规则.同济大学土木工程防灾国家重点实验室振动台试验室对其进行了震振动台试验研究，将模型分析结果与振动台试验结果进行了比较，以验证本文提出的本构模型、参数确定方法及选用分析模型的有效性和合理性.由于ABAQUS建模工作较为复杂，本文首先在PKPM中建模，然后借助PKPM-ABAQUS转化程序［9］将模型导入到ABAQUS中进行计算.

1 弹塑性损伤本构模型参数的确定

1.1 控制损伤演化参数取值的确定

由文献［8］可知本构模型拉、压损伤变量计算公式如下：

式中：a±和b±均为控制损伤发展参数（上标“+”表示受拉参数，“-”表示受压参数）；Y±为损伤能量释放率；Y±0为损伤能量释放率阈值，可通过混凝土单轴试验确定.

如果没有一个实用的方法来确定上述6个参数的取值，则模型较难应用于实际工程中.

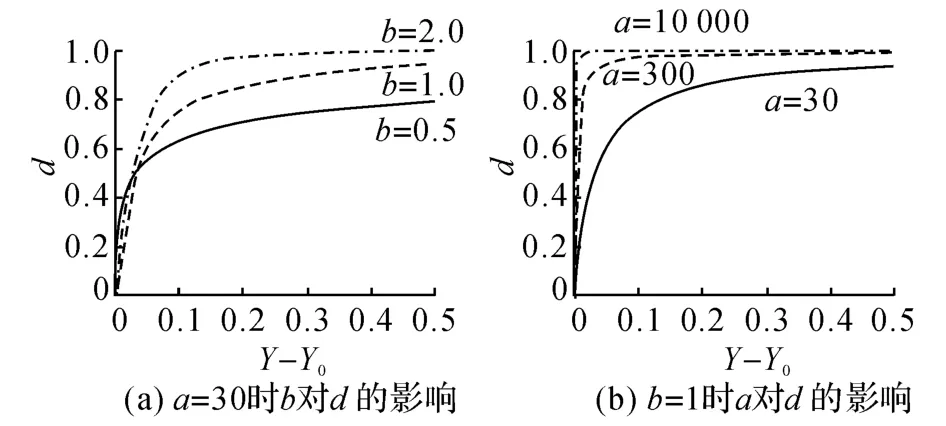
图1 a和b对损伤的影响Fig.1 Effect of a and b

图2给出了参数和的变化对混凝土单轴受压应力-应变骨架曲线的影响.从图2可以看出，参数对模型极限受压应力影响较大，越小模型计算极限应力越小；参数主要影响曲线下降段的斜率，越小计算曲线下降段斜率越小.

通过计算可得：当初始弹性模量一定（=31000 MPa）时，与混凝土强度存在指数关系，如图3和式（2）所示；当一定（fc=31.14 MPa）时，与（混凝土结构设计规范（GB50010-2010）（后文简称规范）表4.5.1范围内）［10］存在线性关系如图3和式（3）所示.

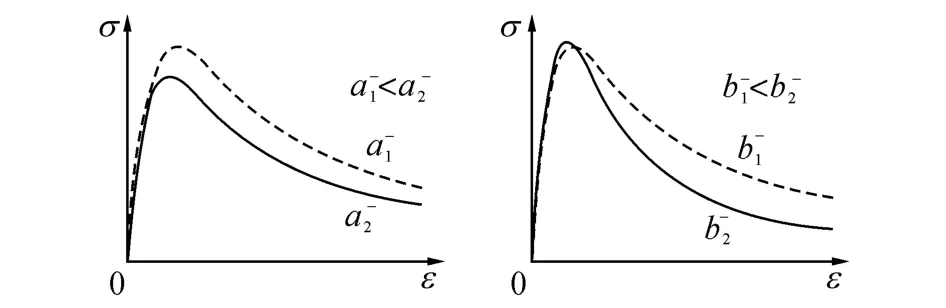
图2 参数、对模型应力-应变曲线的影响Fig.2 Effect of a-and b-on model behavior

图3 a-与f c、E 0 关系Fig.3 Relationship of，fc and E0

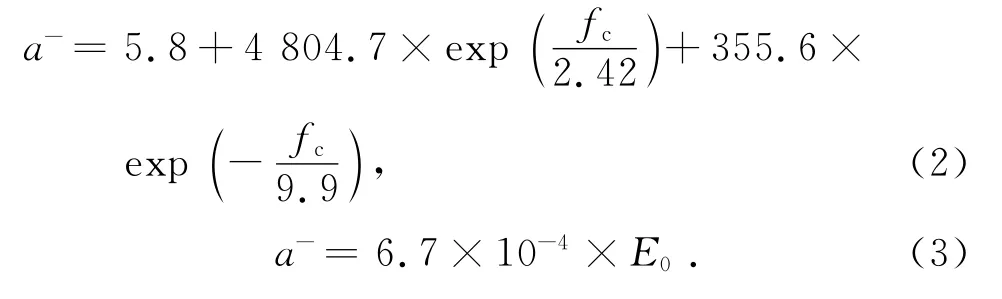
综合式（2）、（3），得出a-与混凝土抗压强度fc和初始弹性模量E0之间的关系如下：

通过以上研究可知，已知fc和E0就可以由式（4）确定a-值.采用式（4）确定a-值，对规范中各强度混凝土材料进行模拟，计算结果与混凝土强度设计值比较如表1.

表1 模型计算强度与规范设计值比较Tab.1 Comparison of calculation results and code___

从表1可以看出，对于规范规定各强度等级混凝土材料给定材料强度设计值和弹性模量，通过式（4）确定a-取值，则模型计算混凝土强度与混凝土规范值符合很好.

对于b-在单轴、双轴加载下，取=0.98［1］，本文建议对于单双轴加载取为1.对于三轴受压加载，由于侧向约束作用，主轴应力-应变曲线与单、双轴加载情况下相比，曲线的下降段更平缓［3］，如图4所示，由图2可知，此时的取值应小于单、双轴加载情况.在实际工程中，模型主要用来模拟混凝土材料的单轴、双轴加载情况，现阶段本文只给出单、双轴加载取值.

图4 双轴、三轴加载主轴应力-应变曲线Fig.4 Principal stress-strain curves under 2D，3D loading

a+、b+控制受拉损伤演化，它们影响受拉加载曲线的下降段，如图5所示，本文参照文献［1］取a+=7 000，b+=1.1.

为初始损伤阈值，当拉、压损伤能量释放率小于时材料处于受拉、受压弹性阶段，当损伤能量释放率超过后材料开始产生拉、压损伤.

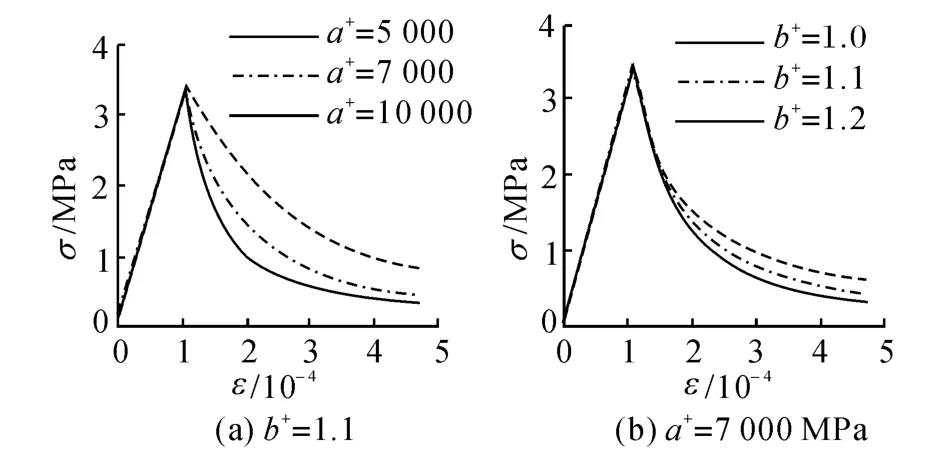
图5 a+和b+对模型受拉曲线的影响Fig.5 Effect of a+and b+on tensile curve of model

对材料单轴受拉应力-应变曲线以及受拉损伤演化的影响如图6（a）、（b）所示.对材料单轴受压应力-应变曲线以及受压损伤演化的影响如图6（c）、（d）所示.

由图6可知，决定混凝土材料的抗拉强度，对材料受压加载应力-应变曲线存在一定的影响.可由单轴加载试验确定.对于受拉，材料在加载到极限抗拉强度前为弹性，应将取为材料单轴受拉加载到抗拉强度时的损伤能量释放率；对于受压，材料在加载到0.25倍抗压强度前为弹性，应将取为材料单轴受压加载到0.25倍抗压强度时的损伤能量释放率.和的计算公式如下：

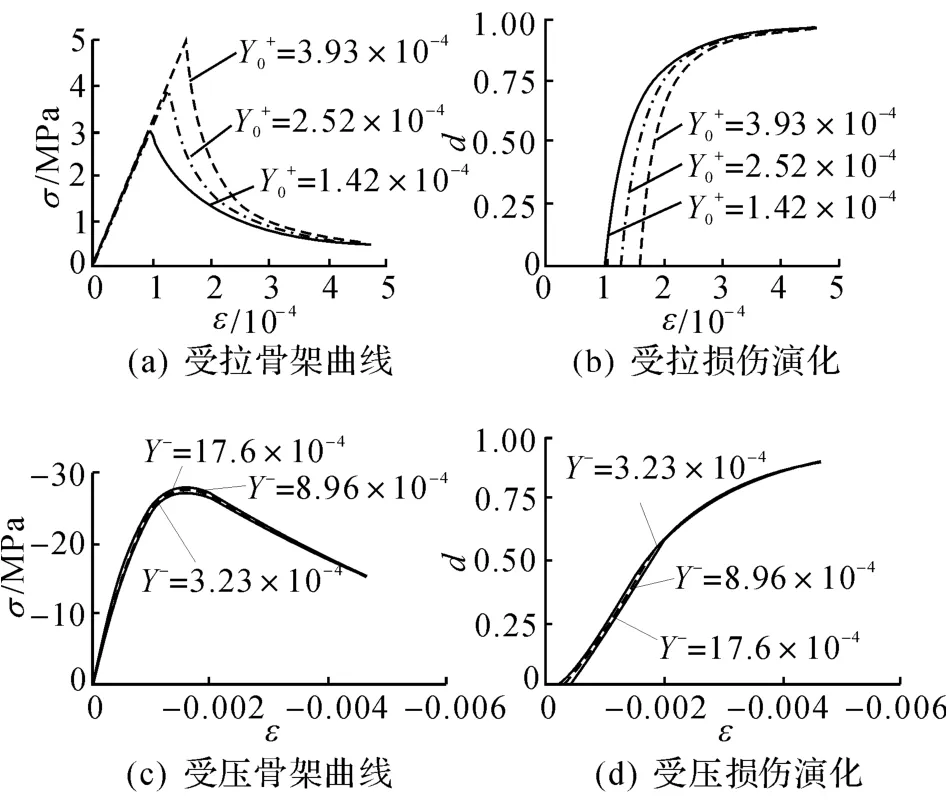
图6 和对模型的影响Fig.6 Effect of and on model

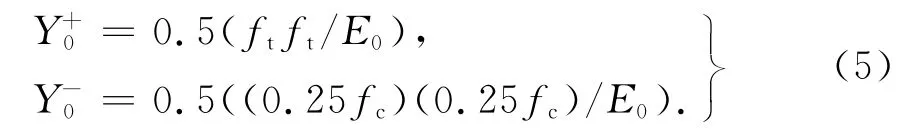
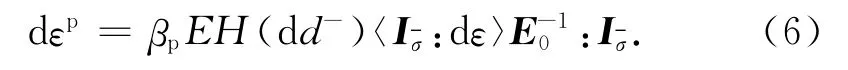
式中：dε表示对ε取微分；E表示材料弹性模量；为单位有效应力张量；参数βp为控制塑性应变大小的参数，如图7所示，对于βp各学者给出了不同的取值［3，11］，本文通过研究发现βp与加载状态有关：双轴、三轴受压加载材料塑性变形比单轴受压加载大.本文建议对于单轴受压加载本文建议取βp=0.1，对于双轴受压加载βp计算如下：

1.2 控制塑性应变参数βp取值确定

文献［8］给出的塑性应变计算公式为

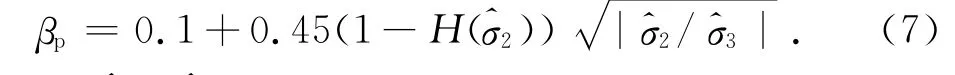
式中：分别表示应力的第2、第3主应力（在双轴受压加载时第一主应力=0）.当＞0时，βp与之间的关系如图8所示.

图7 βp对塑性应变的影响Fig.7 Relationship ofβp on plastic strain

图8 βp 与ˆσ2/ˆσ3之间的关系Fig.8 Relationship betweenβp andˆσ2／ˆσ3

2 试验数值分析

2.1 单、双轴加载试验数值模拟

分别采用本文提出的模型对Kupfer等［12-13］所做的试验进行模拟，并将计算结果与文献中的试验结果进行比较（如图9～11所示，其中图10表示在双轴加载的情况下主次方向不同比例加载时，主加载方向的应力／应变曲线）.文献［12-13］中的试验模拟参数取值：E=31 000 MPa；v=0.2，fc=27.6 MPa；ft=3.5 MPa、a±、b±及的取值按照本文提出的方法确定，分别为a-=28，a+=7 000 MPa-1，b-=1，b+=1.1，βp=0.1+0.45=2.0×10-4，=7.7×10-4.Gopalaratnam试验参数取值：E=31 800 MPa，v=0.2.ft=3.4 MPa，a+=7 000 MPa-1，b+=1.1=1.8×10-4.

从图9～11可以看出，本文提出的本构模型及参数取值方法能较好地描述混凝土材料的各种非线性本构行为.

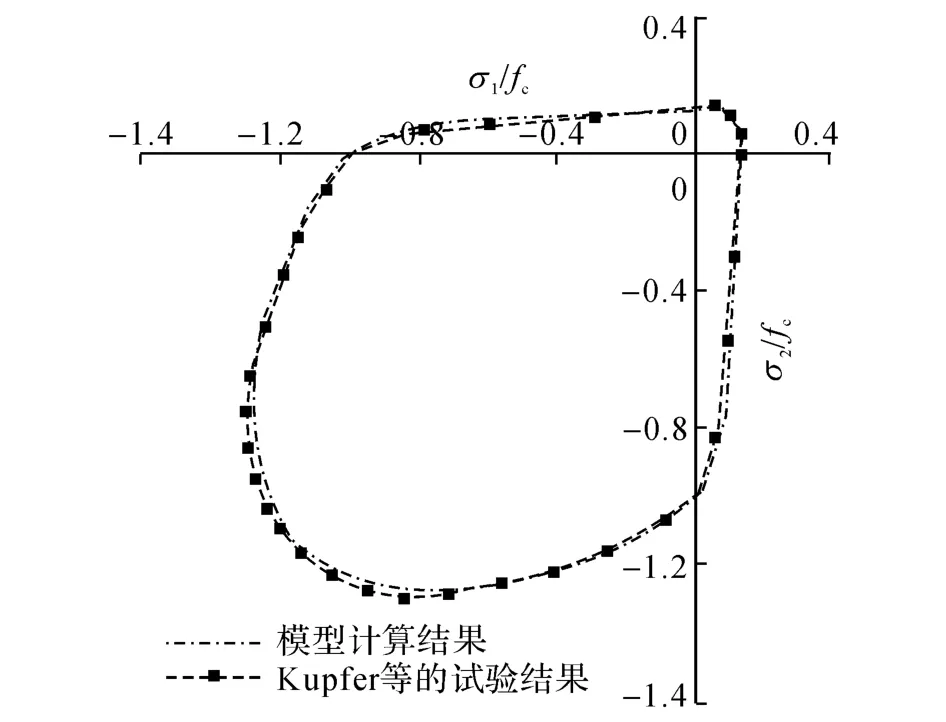
图9 双轴应力作用下的强度包络Fig.9 Biaxial strength envelope under action of biaxial stress

图10 双轴受压加载Fig.10 2D compressive test

图11 单轴受拉反复加载Fig.11 1D cyclic tensile test

2.2 香格里拉酒店数值模拟

上海浦东香格里拉酒店扩建工程位于上海市浦东陆家嘴经济开发区，是由一栋总高度为152.8 m的41层塔楼和一幢4层裙房组成的超高层框架——剪力墙结构.本工程设有地下室2层，地面以上37层，另加避难楼层2层（分别位于10～11层和24～25层）.其中，地下一层、二层的层高分别为3.00和4.55 m；地面以上第1～6层的层高分别为6.05、5.00、5.00、6.00、5.00、5.00 m；第7～35层的层高为3.40 m；第36层的层高为5.40 m，第37层的层高为5.00 m；上下避难楼层的层高为4.50 m，工程总建筑面积为36 200 m2，结构高宽比为4.52.该工程结构的1～4层结构平面如图12（a）所示，塔楼第5层（转换层）结构平面如图12（b）所示，塔楼5层以上的楼层结构平面如图12（c）所示.

本工程塔楼部分总高度为152.8 m，顶部钢桁架局部高度为180 m，结构高度超过了上海市框架——剪力墙结构体系的上限值（140 m）.另外，塔楼结构下部开有宽25.6 m、高23 m的孔洞，结构平面布置不规则.

图12 香格里拉酒店典型楼层平面图Fig.12 Typical floor of Shangri-La Hotel

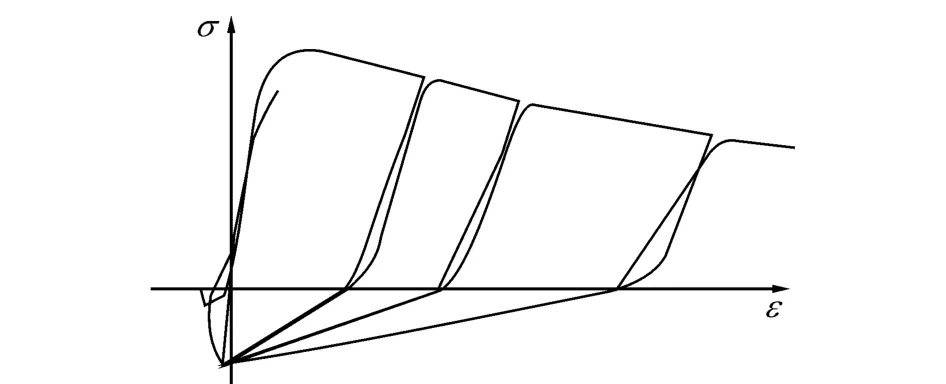
图13 单轴本构模型滞回加载曲线Fig.13 Uniaxial concrete model proposed by authors

香格里拉酒店在PKPM中所建模型如图14（a）所示，然后用PKPM-ABAQUS转换程序［9］将PKPM中模型转换生成ABAQUS模型，如图14（b）所示，在ABAQUS中梁柱构件采用纤维模梁单元模拟，剪力墙构件采用4节点减缩积分壳元模拟，一维本构模型采用笔者提出的非线性弹性本构模型［14］，如图13所示；二维本构模型采用作者建议的弹塑性损伤本构模型［8］，参数取值按本文提出的方法确定.采用显式积分算法求解，在本构材料中考虑了刚度阻尼力，材料阻尼取其第一振型临界阻尼的3%［15］，在材料中加入阻尼力的算法如下［15］：

只考虑刚度阻尼，无损材料阻尼力表达式为¯σvis=βk E0∶˙ε，其中βk为刚度组合系数，˙ε为ε随时间的变化率.

Cauchy黏滞阻尼应力σvis可表示为

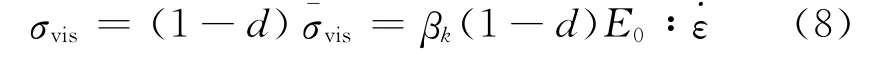
弹塑性损伤本构关系为

则总应力可表示为

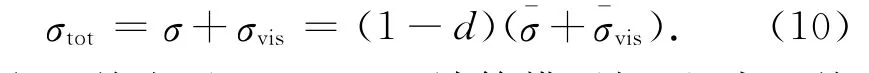
图15给出了ABAQUS计算模型振型，表2给出了PKPM和ABAQUS的计算模型振动周期T与振动台试验结果的比较.

图14 结构数值模型Fig.14 Numerical model of structure

图15 香格里拉酒店振型图Fig.15 Vibration model of Shangri-La Hotel

表2 结构振动周期比较Tab.2 Comparison of vibration period of structure s

从表2可以看出，PKPM计算模型前4个振型周期与试验结果符合较好，说明PKPM数值模型的准确性较好；ABAQUS计算模型前4个振型周期与PKPM计算结果符合较好，证明转换程序能准确有效地将PKPM模型转换为ABAQUS模型.

为了验证本构模型在分析实际复杂工程结构时的有效性，本文对上述工程进行非线性时程反应分析.输入地震波为上海人工波SHW2，如图16所示.地震波从χ方向（见图14）输入，结构顶层位移时程计算结果与振动台试验结果比较如图17所示.

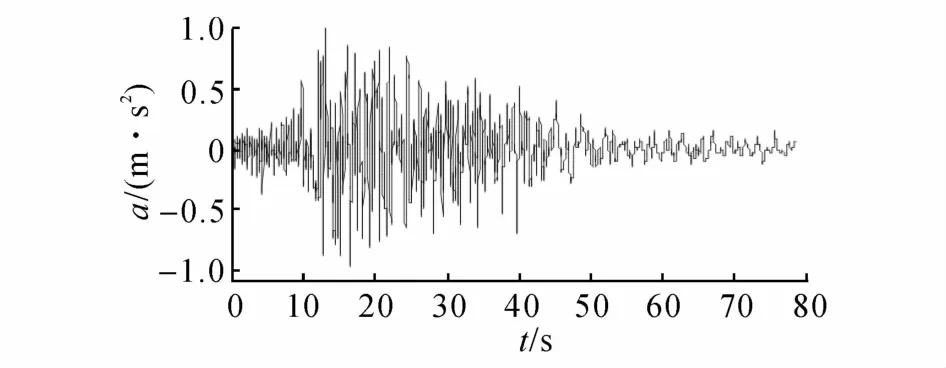
图16 上海人工波SHW2时程Fig.16 Shanghai artificial wave SHW2

图17 顶层x方向位移时程比较Fig.17 Comparison of roof displacement time history inχdirection

从图17可以看出顶层位移时程计算结果与试验结果总体符合较好，位移峰值出现在14 s左右，且试验峰值与计算峰值十分接近，最大峰值过后试验位移迅速衰减，此后2个位移时程峰值试验结果均小于数值分析结果.图18为典型楼层位移时程曲线.图19为楼层位移包络图计算结果与试验结果的比较.

从图19中可以看出，楼层最大位移包络图计算结果与试验结果符合较好，计算结果比试验值略大，结构楼层位移在第3层出现明显拐点表明结构在第3层较为薄弱.图20为最大层间位移计算结果与试验结果的比较.

图18 主要楼层计算位移时程Fig.18 Displacement-time history of main floors

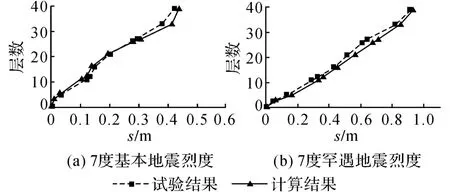
图19 楼层位移包络图Fig.19 Displacement envelope of floors

为了研究结构的破坏形态，下面分别给出罕遇地震作用下，结构剪力墙构件在不同时刻的应力云图、受拉损伤云图及受压损伤云图.结构剪力墙构件关键时刻应力变化云图如图21所示.从图21可以看出，结构在地震波加载到12.4 s、16.0 s时顶层位移为正，结构向右偏移，结构右侧应力大于左侧应力；结构在14.0 s和35.6 s的顶层位移为负，结构向左偏移，结构左侧应力大于右侧应力.以上分析结果与结构实际受力情况一致.

图20 层间位移Fig.20 Story drift

图21 剪力墙结构应力分布图Fig.21 Stress distributions of shear wall

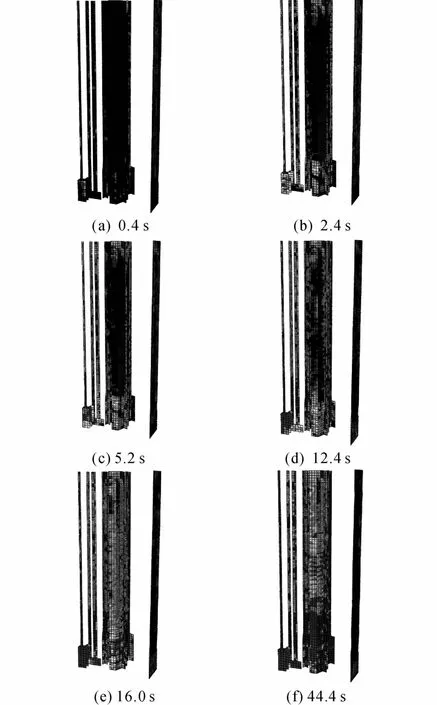
图22 某剪力墙结构受拉损伤分布图Fig.22 Tnsile damage distributions of shear wall

结构剪力墙构件受拉损伤云图如图22所示.从图22中可以看出，结构受拉损伤发展很快，结构在0.4 s产生明显受拉损伤，此后损伤迅速发展.受拉损伤最初集中在裙房、裙房与塔楼结合楼层以及结构右侧剪力墙构件，之后逐步蔓延至整个结构.同时受拉损伤在地震波加载前期主要在左右两侧剪力墙结构上发展，之后逐步蔓延至中间部位，在地震波作用后期，除上部少数楼层，其他部分均存在较大的受拉损伤.

结构剪力墙构件受压损伤云图如图23所示.从图23可以看出，结构剪力墙构件在5.2 s时裙房和塔楼结合产生明显受压损伤，此后受压损伤迅速发展，到34.8 s结构产生较大受压损伤.同时结构在下部裙房以及裙房和塔楼结合处受压损伤较大.结构在34.8 s和44.4 s受压损伤云图比较接近，可见到34.8 s结构大部分受压损伤发展完成，此后受压损伤发展缓慢.

图23 剪力墙结构受压损伤分布图Fig.23 Compressive damage distribu t ion of shear wall

3 结 论

（1）使用本文提出的参数确定方法，实际使用中只须给定材料抗拉、抗压强度和弹性模量就能方便地确定全部参数的取值，便于在实际建筑结构的分析中使用.

（2）分析结果与振动台试验结果在结构自振频率、振型形态、最大楼层位移及顶层位移时程等匹配较好，说明本文提出的本构模型及选用的构件分析模型和分析方法是有效的，适合实际复杂高层建筑结构的非线性分析.

（3）在实际建筑结构的分析中，弹塑性损伤本构模型不但可以得到结构在外力作用下的应力和位移响应，而且可以同时得到不同状态下结构的损伤分布.这种损伤过程被实时地反映在结构的非线性分析过程中，便于分析者直观地把握结构的破坏形态.

（

）:

［1］VOYIADJIS G Z，TAQIEDDIN Z N.Elastic plastic and damage model for concrete materials：Part I-theoretical formulation［J］.International Journal of Structural Changes in Solids-Mechanics and Applications，2009，1（1）：31- 59.

［2］WU J Y，LIJ，FARIA R.An energy release rate-based plastic damage model for concrete［J］.International Journal of Solids and Structures，2006，43（3／4）：583- 612.

［3］FARIA R，OLIVER J，CERVERA M.A strain-based plastic viscous-damage model for massive concrete structures［J］.International Journal of Solids and Structures，1998，35（14）：1533- 1558.

［4］LEE，Jand FENVES，G L.A plastic-damage model for cyclic loading of concrete structures［J］.Journal of Engineering Mechanics，1998，124：892- 900.

［5］JU，J W.On energy-based coupled elasto-plastic damage theories：constitutive modeling and computational aspects［J］.International Journal of Solids and Structures，1989，25（7）：803- 833.

［6］OLLER S，ONATE E，OLIVER J，et al.Finite element nonlinear analysis of concrete structures using a plastic damage model［J］.Engineering Fracture Mechanics，1990，35：219- 231.

［7］SHEN X，YANG L，ZHU F.A plasticity-based damage model for concrete［J］，Advances in Structural Engineering，2004，7（5）：461- 467.

［8］齐虎，李云贵，吕西林.基于能量的弹塑性损伤实用本构模型［J］.工程力学，2013，30（5）：172- 180.QI Hu，LI Yun-gui，LV Xi-lin.A practical elastic plastic damage constitutive model based on energy ［J］.Engineering Mechanics，2013，30（5）：172- 180.

［9］刘慧鹏，李云贵，周新炜.PKPM与ABAQUS结构模型数据接口开发研究及应用［C］∥第二届工程建设计算机应用创新论坛论文集.上海：［s.n.］，2009：487- 494.LIU Hui-peng，LI Yun-gui，ZHOU Xin-wei.The development and application of PKPM and ABAQUS structure model data interface［C］∥The Second Sonstruction Engineering Computer Application Innovation Forum Proceedings.Shanghai：［s.n.］，2009：487- 494.

［10］GB 50010-2010混凝土结构设计规范［M］.北京：中国建筑工业出版社，2010：19- 20.

［11］吴建营，李杰.考虑应变率效应的混凝土动力弹塑性损伤本构模型［J］.同济大学学报，2006，34（11）：1427- 1430.WU Jian-ying，LI Jie.Elastoplastic damage constitutive model for concrete considering strain rate effect under dynamic loading［J］.Journal of Tongji University：Natural Science Edition，2006，34（11）：1427- 1430.

［12］KUPFER H B，HILDORF H K，RUSCH H.Behavior of concrete under biaxial stresses［J］.Journal of the Engineering Mechanics Division，1969，6（8）：656- 666.

［13］GOPALARATNAM V S，SHAH S P.Softening response of plain concretein direct tension［J］.Journal of the American Concrete Institute，1985，82（3）：310- 323.

［14］齐虎，李云贵，吕西林.箍筋约束混凝土单轴滞回本构实用模型［J］.工程力学，2009，28（9）：95- 102.QI Hu，LI Yun-gui，LV Xi-lin.A practical confined concrete constitutive model under uniaxial hysteresis load［J］.Engineering Mechanics，2011，28（9）：95- 102.

［15］LEE J，FANVES G L.A plastic-damage concrete model for earthquake analysis of dams［J］.Earthquake Engineenng and Structural Dynamics，1998，27（9）：937- 956.