基于遗传算法的机翼壁板扫描路径优化

艾小祥，俞慈君，方 强，陈 磊，方 伟，沈立恒

（1.浙江大学 机械工程学系，浙江 杭州310027；2.中国商飞上海飞机制造有限公司，上海200436）

在现代制造工业中，特别是在模具制造、武器装备、航空航天等领域，复杂自由曲面的广泛应用导致高精度曲面测量的需要越来越多，传统的人工测量方式已无法满足现代化精密测量的要求，如何快速、准确地完成产品曲面的精确测量成为研究热点.

近年来，集光、机、电技术于一体的三维激光扫描技术发展迅速.该技术采用非接触式的主动测量，可以进行大面积、高密度的空间三维数据采集，具有点位测量精度高、采集空间点密度大、速度快以及可以测量柔软和易变形物体等特点，相比于三坐标测量机（coordinate measuring machine，CMM）优势明显［1］.

为提高激光扫描测量的质量和效率，对扫描路径的规划显得尤为重要.Lee等［2］根据CAD模型估计初始扫描路径，再根据各样点的宽度、景深以及角度等参数更新路径，此方法仅从扫描的可行性上考虑，没有对扫描的路径进行优化.Zhao等［3］将三坐标测量机和激光扫描测量结合起来，从CAD模型中获取几何信息，考虑2个样点间的可能路径，该方法测出的样点比较准确，但是没有完全实现路径的自动化生成.李剑［4］提出了一种曲面零件的多模分段自适应测量规划方法和矩形自适应测量规划方法，此方法主要从安全角度考虑，使测点分布更加合理，避免碰撞.李雄兵等［5］在超声检测中对路径进行2次规划，先对测量点人工进行规划，根据已测点的三维坐标分析曲面曲率，再根据曲率实现测量点的自动规划，此方法步骤比较繁琐.

在飞机机翼壁板数字化装配过程中，需要快速扫描机翼壁板的蒙皮外形，用于指导装配过程和评价装配质量.利用机床或机器人携带扫描仪，实现自动化扫描测量和评价是飞机壁板装配的必然趋势.传统的扫描路径规划方法扫描路径长、效率低，而且扫描点的质量无法保证.本文分析激光扫描仪扫描样点时的倾角、距离及扫描宽度等约束条件，并使用遗传算法对扫描路径进行优化以减小扫描路程和扫描过程中机器人的姿态变换次数，从而提高扫描效率.相比于传统的方法，本研究运用DELMIA软件平台进行扫描仿真，扫描仪满足约束条件，从而验证优化路径的可行性.

1 手持式激光扫描仪的扫描约束

本研究所采用的手持式激光扫描仪（T-Scan）以三角形原理为基础测量被测表面到激光出射口的距离，再通过扫描仪相对于激光跟踪仪的空间位姿合成得到扫描点的空间坐标［6］，图1为手持式激光扫描仪实物图.

图1 手持式激光扫描仪Fig.1 Leica T-Scan

为了顺利扫描曲面上的点，扫描仪需满足几个约束条件，如图2所示.Pi和Ni分别表示曲面上被扫描第i个点和它的单位法向量，点O表示激光扫描仪位置，Bi表示两激光边界扫描线的平分线，扫描仪约束条件包括倾角（θ）、景宽（field of view，FOV）、景深（depth of view，DOV）等约束.

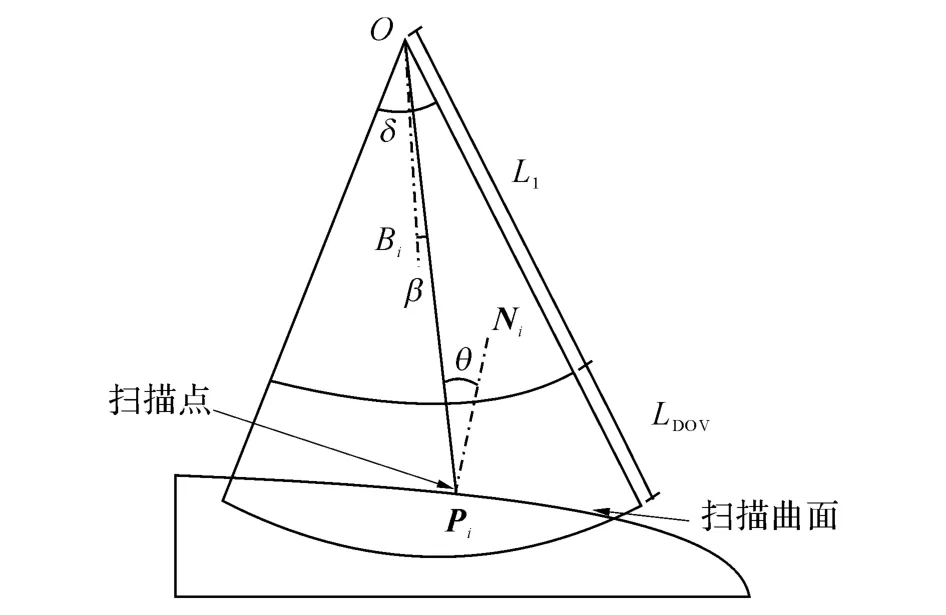
图2 扫描仪扫描约束Fig.2 Scanning constraints of T-scan

1）扫描仪倾角：扫描点到扫描头的连线和扫描点法向量的夹角（设为θ）应小于约束角γ.

式中：-di为单位向量，

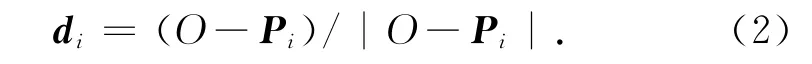
2）景宽 （FOV）：扫描点应在对应某条激光条纹长度范围内，设（-di）与Bi之间的夹角为β.

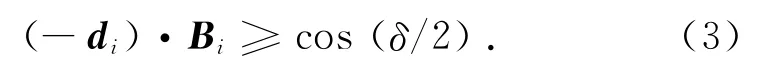
式中：δ为景宽角，为激光扫描仪的固定参数.

3）景深（DOV）：被测点必须在一个偏离激光源的指定范围内：

4）其他约束：入射光不被扫描物体挡住以及扫描仪运动时不发生碰撞.

Hageniers［7］的研究表明：除了上述因素，影响扫描精度的因素还有很多，如：被测表面的颜色、材料以及粗糙度等，本文对这些因素不予考虑.

2 路径扫描的传统方法分析

在工程项目实际应用时，扫描测量系统通过机器人固定激光扫描仪，并利用机器人控制激光扫描仪在测量区域移动进行扫描测量.当扫描仪没有姿态调整时，扫描仪前端面位于同一平面上.决定扫描效率的2个关键因素为扫描路径的总长度和扫描仪的调姿次数.当扫描仪沿着一个平面运动时，处于同一个姿态，无需调姿.故这2个因素也可以表示为扫描仪所走路径总长度和总平面数，以这2个指标评价各方法的优劣.

利用二维平面可以实现曲线的自动跟踪测量，常见的方法包括阶梯式跟踪法、直线式跟踪法［8］.

1）阶梯式跟踪法：原理如图3所示，连续判断曲线上被扫描点到跟踪平行面的距离是否在景深范围之内，当距离超出范围时，向上或向下调整扫描平面.此方法的优点是计算简单，缺点是平面调整频繁，平面数多，且由一个平面换到另一个平面时产生较大的空行程.

将此方法应用于扫描仪的三维扫描，由于扫描为同一姿态，即只考虑了景深这一约束条件，当曲面上被扫描点法矢变化较大时，扫描仪倾角约束无法保证，即无法完成扫描.此方法适用平坦性很好的曲面，应用范围受限.

2）直线式跟踪法：原理如图4所示，由开始几个测量点拟合出一个平面，然后平面进行延伸，不停地判断被扫描点和扫描仪之间是否满足约束条件，当被扫描点不满足约束条件时，拟合下一个平面.

将此方法应用于扫描仪的三维扫描，扫描路径随曲面而变化，扫描质量较好，但路径总体形状接近弧形，路径长度较长，跟踪面数较多.

图3 阶梯式跟踪法Fig.3 Stairs-shaped tracing method

图4 直线式跟踪法Fig.4 Linear tracing method

综合以上2种方法的优缺点可知，为提高扫描效率，应使平面数尽量少，即同一个平面扫描的样点数尽量多；在样点数一定的情况下，应使扫描路径尽量短.基于这2种原则，拟采用图5所示的跟踪方法，相比于前2种方法，大大减少了跟踪面数量，在扫描路径间增加了快速调姿路径以防止漏扫描.虽然该方法增加了总路径，但是所增加路径较少，总体效率较高.本文对各平面段进行三维空间的调姿优化，在满足约束的条件下，通过减小各段的扫描长度来减小总长度.

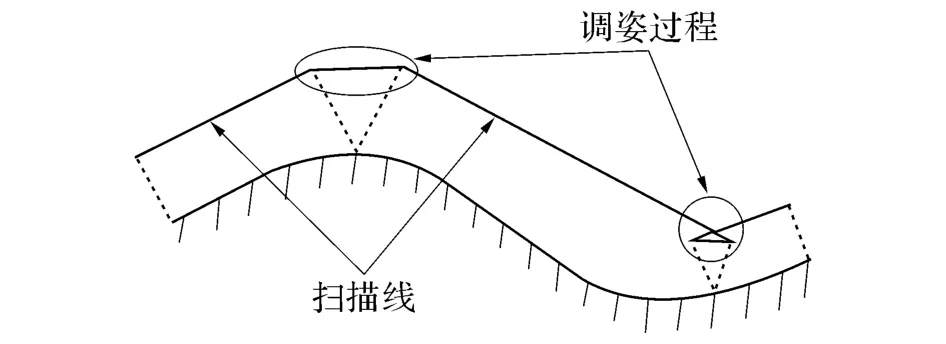
图5 本研究所采用的跟踪法Fig.5 Tracing method used in our research

3 扫描路径规划

3.1 扫描路径规划的总体策略

扫描对象为机翼壁板蒙皮，总体形状接近三角形，边界由十多段线段组成，二维投影示意图如图6所示.

图6 机翼壁板蒙皮Fig.6 Skin of airplane wing

行切法是数控机床加工中常见的刀具走刀方式［9］.受此启发，扫描仪扫描机翼壁板蒙皮时可以采用此方法.壁板为大尺寸件，离散样点多，行切法求取路径边界点简单、方便；壁板中间没有凸台，行切法不存在类似于数控加工中的抬刀动作，有利于充分利用机床的进给速度，扫描效率高，所用时间少.

对于行切法扫描，当型腔轮廓比较复杂时，行切方向的选择是一个比较复杂而重要的问题.研究表明［10］：采用边界轮廓中边长最长的直线边的角度作为行切角度时（如图7所示），路径较短.本文采用此方法.

针对机翼壁板这种自由曲面，为保持曲面重构和CAD建模方式的一致性，采用“曲面-曲线-样点集”的递归分解方法对连续曲面进行数字化离散.由一组平行平面和曲面相交得到一组曲线，再对这组曲线进行等弧长离散，得到蒙皮样点，并将这些样点投影至一个已知X-Y平面，得到如图8所示的样点.

图7 平行于最长边的行切法Fig.7 Direction-parallel path based on the longest edge

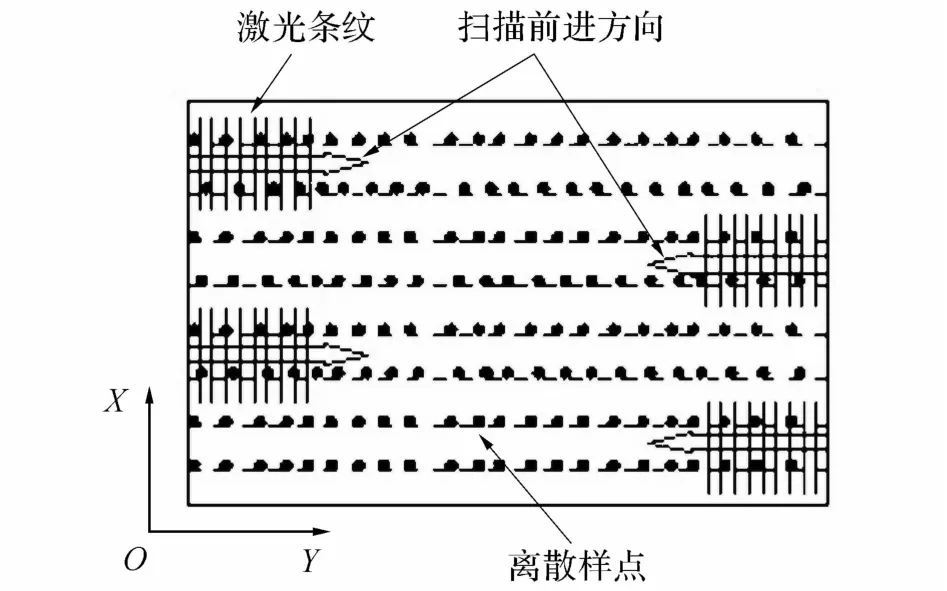
图8 蒙皮离散的样点集及扫描方向Fig.8 Sampled points and scanning directions

3.2 基于最小二乘法的扫描路径生成

在得到机翼壁板蒙皮上样点的理论三维坐标及法矢信息后，为实现样点的扫描，可采用曲面的自动跟踪测量法.扫描仪一次可以扫描多条曲线上的点（如图8所示），且扫描仪的前进方向和激光出射平面垂直.根据扫描仪的平均扫描宽度，可确定一次扫描的曲线条数，将这些曲线上的点作为一个整体（设为Point Array）考虑，按前进方向（Y轴）的坐标值排序.

以最小二乘法为基础，对初始点集Point Array进行分组的流程图见图9.

图9 点集分组过程Fig.9 Grouping of sample points

最小二乘法拟合平面的基本原理是：所求系数a、b、c应使偏离的平方和E为最小，设所求平面方程为

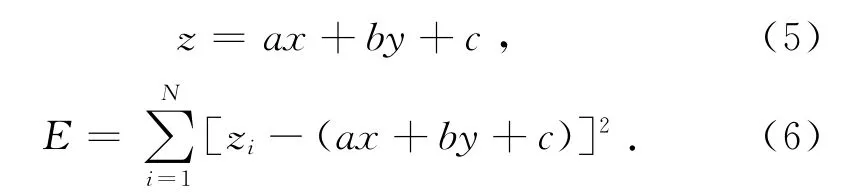
式中：N表示点的数量.

将一个前进方向上的点集Point Array分组之后，得到各个点组对应的最小二乘拟合平面方程，此最小二乘平面与壁板相交.扫描仪扫描时，为避免与壁板碰撞，应使所有样点位于平面一侧，因此必须对所得平面进行平移.扫描完一个点组后，在开始扫描下一个点组之前，扫描仪须进行空间的三维调姿，其过程示意图如图10所示.

4 基于遗传算法的总体扫描路径优化

由前文分析可知，整个扫描过程分为扫描阶段和调姿阶段，当点集分组完成后，扫描过程总时间由调姿次数及扫描总路径长度决定，为了提高扫描效率，本文以扫描总时间作为目标函数进行优化.

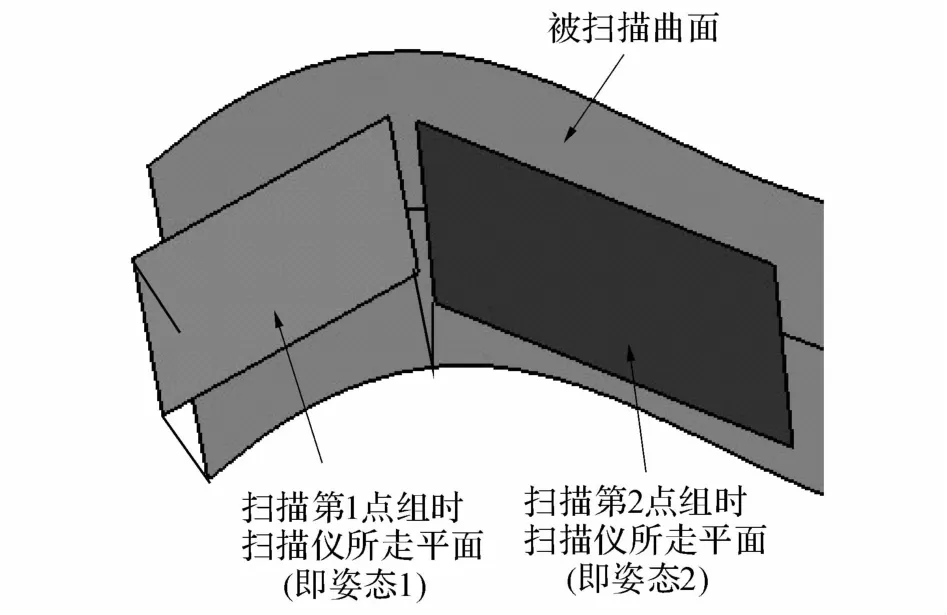
图10 扫描姿态三维图Fig.10 Graphic model of scanning pose

设整个过程总时间为tsum，总平动时间为ts，总调姿时间为tt，有

4.1 总体扫描路径优化函数的建立

对点集进行分组之后，取第一组作为示例进行分析，不妨设此组样点总数为n，第一点为d，最后一点为g，如图11所示.此组点最小二乘拟合得到的平面P0方程为

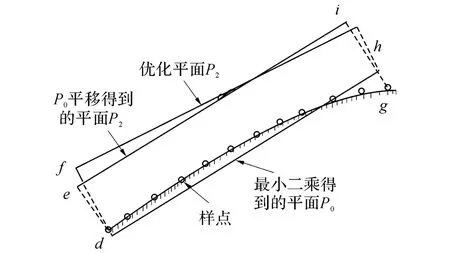
图11 最小二乘平面及优化平面Fig.11 Least squares plane and optimized plane

若扫描仪按平面P1运动，扫描仪所走过的路径长度为‖e-i‖，本文优化目标为在扫描样点确定的情况下，找出一个服从于总体最优运动平面P2，设P2

方程为

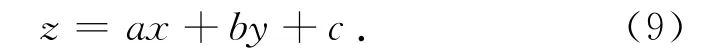
式中：a、b、c为需要优化的参数.设此时扫描仪所走总长度为

式中：f表示扫描第一点时的扫描仪位置，h表示扫描最后一点时的扫描仪位置，且向量都垂直于平面P2.第1点d和最后一点g的三维坐标已知，D1为关于a、b、c的函数.

扫描仪完成此段路径的平均扫描速度为v，故第1段扫描所用时间t1为

扫描仪开始第二组扫描前，需由第一组最后一个位置h换到下一组第一个位置（类似于第一组的点f），设下一组第一个位置为f′，扫描仪可以在点h运动至点f′的同时完成调姿，调姿过程平均移动速度可设为v′，故调姿过程所用时间t′为

整个过程包括扫描及调姿，故完成第一组点所用总时间为

同理可得其他各组扫描所用时间，故总时间为

为了使得扫描仪在实现扫描可行性的情况下，所用总时间最短，令X= ［a，b，c］T，即求时间函数F（X）的最小值.可得优化模型函数为

约束条件为

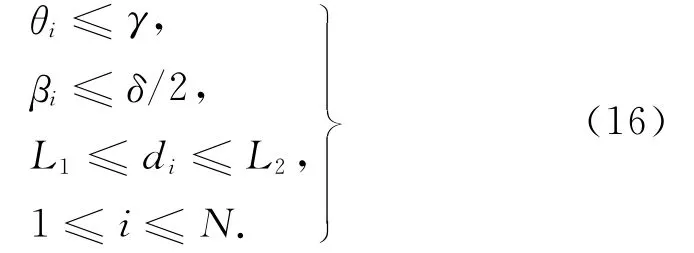
式中：θi为扫描仪倾角，βi为扫描仪到扫描点连线与景宽角平分线的夹角，d i为扫描仪与扫描点间的距离，且θi，βi及d i都为关于X的函数.γ、δ、L1及L2都为扫描仪的内部参数，γ表示最大倾角约束，δ表示景宽角约束，L1为最小景深值，L2为最大景深值，N为点的个数，这几个参数都为固定值，含义见图2中的标准.此时问题转化为单目标多元函数在既定约束条件下最优解的数学问题.

4.2 遗传算法求最优值

遗传算法是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法，不依赖于梯度信息，对于求解非线性约束与无显式数学表达式问题非常有效［11-12］.遗传算法寻优的主要过程包括设计染色体（编码与解码）、计算适应度、选择、交叉及变异等，详细过程如下：

1）设计染色体（编码与解码）.通过一定长度的二进制符号来表达染色体的值，其等位基因由二值｛0，1｝组成.假设染色体X的取值范围为［P1，P2］，若用长度为k的二进制来编码，则可以产生2k种个体.此编码精度为

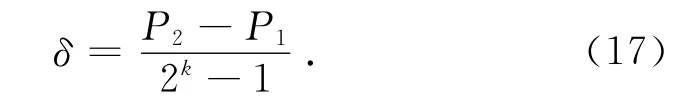
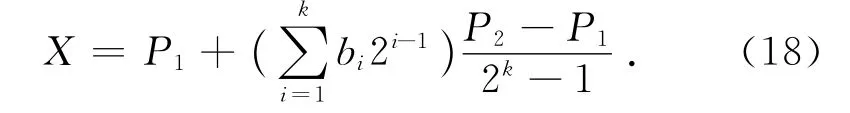
取染色体长度为k=15，如X=100 011 010 100 111表示一个染色体.由于最小二乘法产生的个体是较优值，为了加快算法的效率，只须在a、b、c值的附近寻优.设每个变量的正负20%为其寻优范围，如a的取值范围为［0.8a，1.2a］.为了加快优化速度，应使a、b、c的值为初始个体之一，故在初始化群体中，都存在着X=100 000 000 000 000的染色体.

2）约束条件的处理.遗传算法中对于约束条件的处理，显得尤为重要，即如何在满足约束的条件下，使目标函数最优化.目前主要采用的方法为罚函数法，罚函数法的基本思想是对在解空间中无对应可行解的个体计算其适应度时，处一个罚函数，降低该个体的适应度，使个体被遗传到下一代群体中的概率减小［13］.根据扫描仪的倾角、景宽以及景深约束构造如下罚函数.

扫描仪倾角约束罚函数H1（X）为

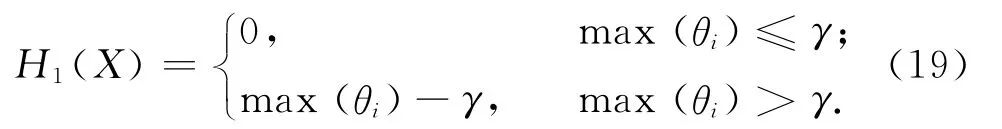
景宽角约束罚函数H2（X）为

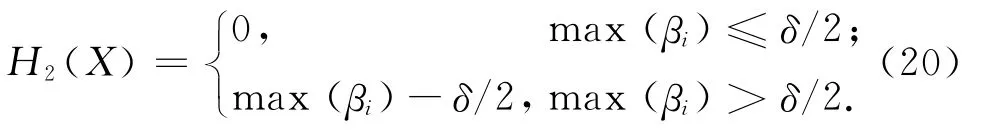
最小景深约束罚函数H3（X）为

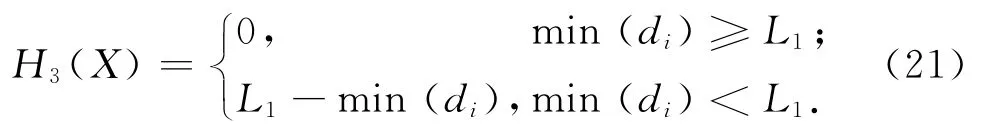
最大景深约束罚函数H4（X）为

令总罚函数为

引入二次罚函数后，目标函数可以表示为

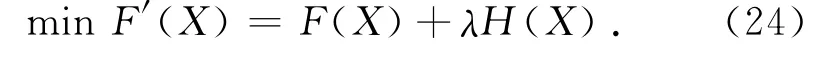
式中：λ为罚因子，一般取较大的正数，本研究取1 000.

3）计算适应度（个体评价）.适应度表示个体遗传至下一代的概率，应满足通用性强、计算量小、合理、单值以及非负等条件，本文所求目标函数为最小值问题，对目标函数做如下变换可得适应度函数

为了确保每一个体均有按相对适应度遗传到下一代的机会，应计算个体相对于整个种群的相对适应度，即

式中：M为种群大小，F‴（χ）为个体最终被遗传进入下一代的概率.

4）选择.采用轮盘赌与最优个体保存相结合的选择方法，既能保障算法的收敛，又能避免过快陷入局部最优.轮盘赌法选择是指根据个体在群体中的相对适应度来确定其被选择至下一代的概率，让高适应度的个体以较大的概率生存.最优保存策略是指选出群体中最优良的个体不进行后续交叉和变异操作，然后用其替换本代群体中经相关运算操作后适应度最低的个体.

5）交叉和变异.以交叉概率Pc=0.9对个体间的某些位段基因进行交叉运算，以变异概率Pm=0.06对个体的某位基因进行变异操作.

5 优化结果及仿真分析

5.1 优化结果

选用CATIA这一适用于复杂曲面造型设计的CAD软件，以VB对其进行二次开发，可得样点批量化处理的软件.在已知机翼壁板CAD模型的情况下，选取需要扫描的蒙皮，得到蒙皮上大量样点的三维坐标信息及单位法向量.利用本文所述的3种方法计算扫描路径，阶梯式和直线式扫描路径生成规则如下.

1）阶梯式扫描路径生成.由于蒙皮总体形状与平面基本平行，可以令姿态平面与X-Y平面平行.扫描仪的平均扫描距离为86 mm，本文取初始扫描距离为90 mm，即姿态平面与各组点集的第一个点的距离为90 mm，并判断姿态平面上扫描仪位姿与后续点的约束情况，当不满足约束条件时，向上或向下调整平面.

2）直线式扫描路径生成.由不在同一曲线上的前3个样点确定某个平面，平移此平面至各约束条件都满足的最远位置，判断此姿态平面上扫描仪位姿与后续点的约束情况，当不满足约束条件时，生成下一个点集组，产生新的姿态平面.

最终扫描路径示意图如图12所示，为验证本文方法的可行性，从机翼壁板蒙皮扫描路径中选取6条路径，对这6组点集进行自动化分组并优化，并将本文方法的结果与直线式跟踪法、阶梯式跟踪法进行对比.

图12 壁板蒙皮扫描示意图Fig.12 Scanning paths of skin

蒙皮尺寸大，翼展达几米，扫描仪平均扫描宽度为90 mm，需要几十次巡回完成所有扫描，单个图无法表现出所有扫描路径.为了清楚展现最终扫描路径，暂取第1组作为实例，3种方法最终的扫描路径及扫描仪姿态如图13～15所示.

图13 阶梯式扫描路径图Fig.13 Scanning paths of stairs-shaped method

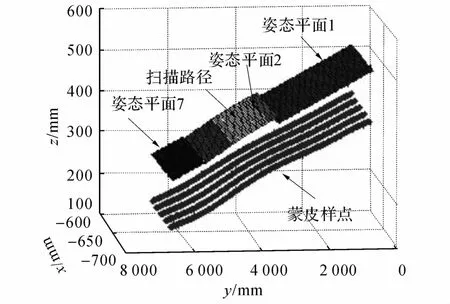
图14 直线式扫描路径图Fig.14 Scanning paths of linear method

以上6组路径扫描总长度D如表1所示.对应于表1，各组别的扫描面数n如表2所示.每段扫描线中有加速、减速过程，加速、减速时间为

由前文可知整个过程的总时间为

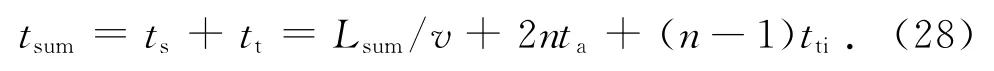
式中：tti为单次调姿时间，v为平均运行速度.搭载扫描仪运动拟采用KUKA机器人.根据激光扫描仪的参数，考虑运行的平稳性及安全性，确定扫描运行速度为v=0.12 m／s，加速度为a=0.5 m／s2，各姿态间调姿距离及角度小且接近，可以令每次调姿时间为tti=1.5 s.依此参数求得扫描仪的加速、减速时间，根据扫描平面数求得各调姿时间，得到每组所需的总时间如表3所示.

图15 本文方法扫描路径图Fig.15 Scanning paths in our research

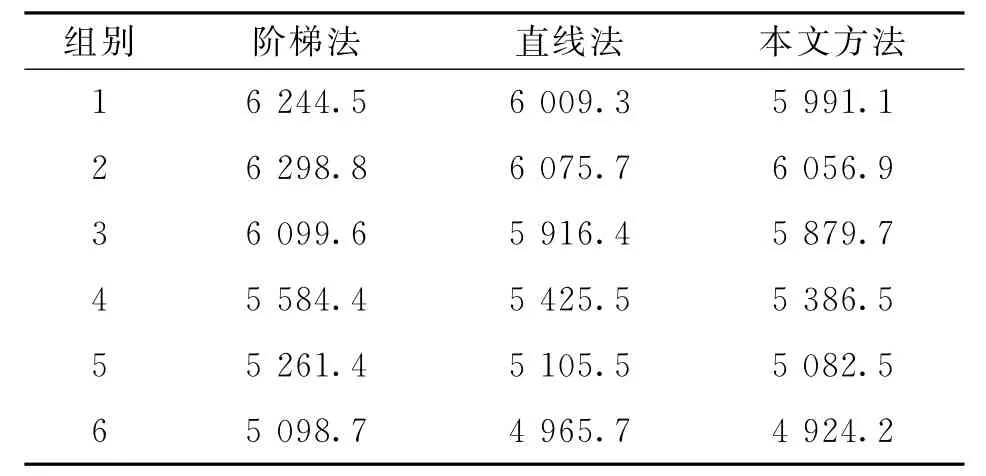
表1 扫描路径长度Tab.1 Scanning length of different groups_ mm

表2 扫描所需面个数Tab.2 Scanning planes of different groups

表3 扫描总时间Tab.3 Scanning time of different groups s__

将表3中各组所用时间制成图如图16所示.

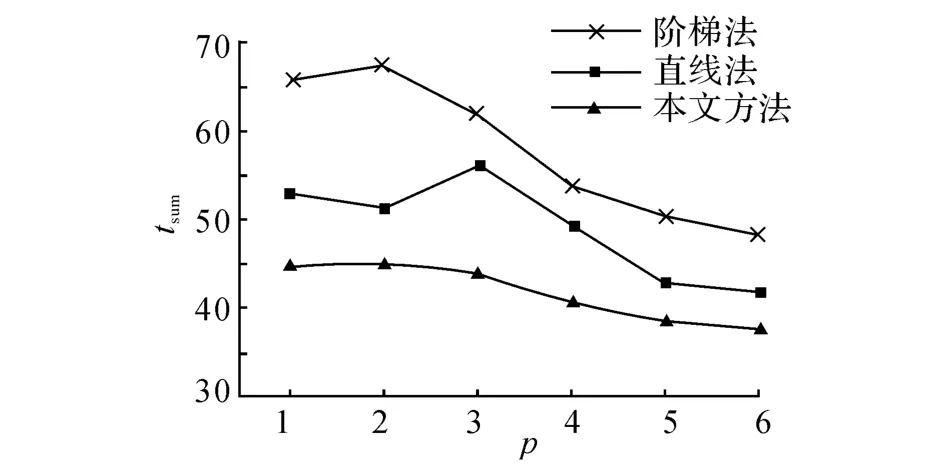
图16 各组点集p在不同扫描方式下的扫描时间Fig.16 Scanning time of different groups

5.2 仿真分析

为了验证优化结果的正确性，即扫描仪沿本文优化的路径运动，可以在符合扫描约束的条件下完成所有样点的扫描.选用DELMIA软件进行扫描过程仿真，通过KUKA机器人及本实验室自主设计的末端执行器搭载激光扫描仪.

为了检测扫描过程中的约束条件，本文利用激光实线法进行检测，即用厚度和宽度值很小的直线实体代替扫描仪出射激光.如图17所示，三角形区域表示扫描有效区域，当扫描点落在此区域时能被扫描，并判断样点法矢和激光线之间的夹角值.

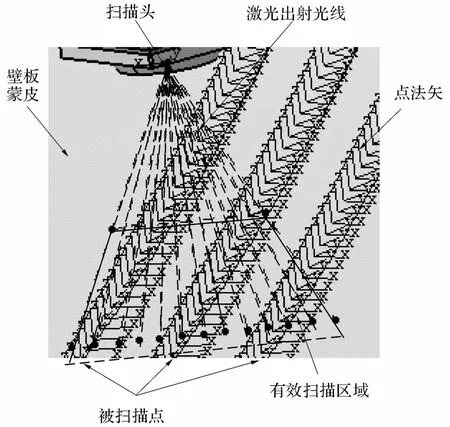
图17 扫描部分局部放大图Fig.17 Drawing of partial enlargement during scaning

为了计算扫描过程时间，将机器人直线运动速度设为0.12 m／s，每次调姿时间为1.5 s，扫描仿真时间如表4所示.由此可得，与传统方法相比，本方法的效率平均提高14.4%.

表4 优化路径扫描仿真时间Tab.4 Scanning time of simulation along optimized path

经仿真分析可知，机器人及末端执行器与壁板不存在碰撞干涉现象，样点全部位于有效扫描区域，且角度符合约束条件，优化出的路径均能够有效地完成蒙皮扫描.

6 结 论

（1）本文提出一种基于遗传算法的扫描路径优化方法，用于机翼壁板扫描时，可减少扫描调姿次数，提高扫描效率.

（2）使用DELMIA软件对优化的扫描路径进行运动仿真.结果表明：经过本文方法优化的路径驱动机器人运动，可以满足扫描约束的要求，扫描效率比传统方法平均提高14.4%.

（

）:

［1］马素文.三维激光扫描在测量中的应用现状［J］.山西建筑，2011，37（9）：207- 208.MA Su-wen.Application status of 3D laser scanner in the measurement ［J］.Shanxi Architecture，2011，37（9）：207- 208.

［2］LEE K H，PARK H.Automated inspection planning of free-form shape parts by laser scanning ［J］.Robotics and Computer Integrated Manufacturing.2000，16（4）：201- 210.

［3］ZHAO H B，KRUTH J，VEN GESTEL N，et al.Automated dimensional inspection planning using the combination of laser scanner and tactile probe［J］.Measurement.2012，45（5）：1057- 1066.

［4］李剑.基于激光测量的自由曲面数字制造基础技术研究［D］.杭州：浙江大学，2001：15- 93.LI Jian.Fundamental research of digital manufacturing of freeform surface based on laser measurement［D］.Hangzhou：Zhejiang University，2001：15- 93.

［5］李雄兵，杨岳，胡宏伟，等.面向超声检测的曲面自动测量［J］，中南大学学报，2010，41（1）：194- 199.LI Xiong-bing，YANG Yue，HU Hong-wei，et al.Complex surface automatic measurement for ultrasonic inspection ［J］.Journal of Central South University，2010，41（1）：194- 199.

［6］海克斯康测量技术（青岛）有限公司.实用坐标测量技术［M］.北京：化学工业出版社，2007：99- 106.

［7］HAGENIERS O L.Recent advances in laser triangulation-based measurement of airfoil surfaces［C］∥Industrial Optical Sensors for Metrology and Inspection.Canada：［s.n.］，1995：2- 22.

［8］宋开臣.三坐标测量机激光扫描测量系统的研究［D］.天津：天津大学，1997：32- 34.SONG Kai-chen.Research of CMM and system of laser measurement ［D］.Tianjing： Tianjing University.1997：32- 34.

［9］程志刚，王巧生.模具高速加工中的走刀路径策略［J］.模具制造技术，2006，8（2）：61- 63.CHENG Zhi-gang，WANG Qiao-sheng.Cutting route strategy in mold high-speed milling［J］.Mold Manufacturing Technology，2006，8（2）：61- 63.

［10］吴光琳，李从心，阮雪榆.型腔加工中的行切方向的优化方法［J］.模具技术，1999，（2）：1- 7.WU Guang-lin，LI Cong-xin，RUAN Xue-yu.Optimization of the direction of direction-parallel cutting in pocket machining ［J］.Die and Mould Technology，1999，（2）：1- 7.

［11］丛明煜，王丽萍.智能化遗传算法［J］.高技术通讯，2003，13（4）：43- 48.CONG Ming-yu，WANG Li-ping.Intelligent genetic algorithm ［J］.High Technology Letters，2003，13（4）：43- 48.

［12］吴沧浦.最优控制的理论与方法［M］.北京：国防工业出版社，2000：108- 226.

［13］雷英杰，张善文，李续武，等.MATLAB遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社.2005：34- 43.