双组分颗粒振动体系中的能量传递与耗散

2015-03-19 01:57张富翁刘传平

浙江大学学报（工学版） 2015年3期

张富翁，王立，刘传平

（1.北京科技大学机械工程学院，北京100083；2.北京科技大学北京高校节能与环保工程研究中心，北京100083；3.攀枝花市经济和信息化委员会综合处，四川攀枝花617000）

颗粒物质广泛存在于自然界中，与人们的生产生活密切相关.作为原材料或催化剂，颗粒物质被广泛应用于化工、冶金和材料生产行业中，诸如矿物分选、气力输送以及材料处理等［1-3］.目前，颗粒物质已成为力学、凝聚态物理和软物质等学科的研究热点.颗粒物质的生产、加工及储运约消耗地球当年所用能量的10%，因此，对颗粒物质的深入研究可起到节能降耗的作用［4］.

面对冶金化工领域日益严苛的工艺要求，如何对生产过程中颗粒材料的运动，特别是组分颗粒的分布进行精准控制已成为目前亟待解决的问题.一些围绕气固两相流（流化床或振动流化床）中颗粒运动的研究成果［5-8］为能够有效预测颗粒的运动和分布奠定了一定的基础.然而，在振动作用下，颗粒物质却表现出许多不同于传统流体或固体的特殊行为，诸如颗粒对流［9］、成拱［10］、表面波［11］及分离［12］等.对双组分颗粒而言，在振动激励下颗粒体系将发生小颗粒在下大颗粒在上的“巴西果”分离［13-14］或大颗粒在下小颗粒在上的“反巴西果”分离［15］.分离形式不仅取决于颗粒物性，同时也与振动参数有关.近年来，研究者从颗粒的受力、几何结构以及表观现象等方面进行了不懈的探索［16-19］.然而，由于颗粒系统复杂的非线性特性，有关分离本质机理的解释仍存在分歧.

离散单元（discrete element method，DEM）法［20-22］能够准确得到振动床内单个颗粒的受力与运动，为分析能量在床层中的传递和耗散规律提供了足够信息.本文采用离散元模拟，从床层底部输入振动能量，分析颗粒床层内能量的传递和耗散规律，并讨论振动参数对颗粒系统能量分布的影响规律.床层采用双组分颗粒混合物，进一步研究了双组分颗粒的分布对能量传递与耗散及系统能量分布的影响，从能量的角度去认识并讨论颗粒的振动分离行为.

1 数学模型

式中：m为颗粒质量；，其中vg为颗粒的速度，¯vg为颗粒平均速度.而颗粒床层内的能量传递则采用傅里叶定律表示：

式中：k为导热系数.k与床层颗粒数量N成指数方关系，k～N y，其中y为指数系数，表征床层内颗粒处于不同的状态（有序或无序），y的取值范围为0～0.5［24-25］.根据床层耗散特性建立床层能量平衡方程

类比于气体，将颗粒的平均脉动动能定义为颗粒温度（T）［23］.基于这一拟气体假设，可以得到如下颗粒温度的表达式：

式中：颗粒碰撞所引起的床层能量耗散γ与颗粒粒径dm、弹性恢复系数e以及颗粒自身温度T等参数相关.

模型计算的物理区域为长方体，长、宽、高为80、80、1 000 mm.计算区域底部为振动床底，作振幅为A和频率为f的正弦振动，床体的位移为s=Asin（2πft），t为运动时间.无量纲振动强度（Γ）的表达式为

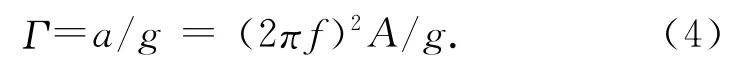
式中：a为振动加速度，g为重力加速度.床底振动前，将一定数量的颗粒随机初始化于计算区域内.计算区域四周为周期边界，颗粒离开侧面边界后会立刻从对面边界以相同的速度进入.

床体振动过程中，床层内颗粒随之发生运动，床内颗粒碰撞时的运动方程为

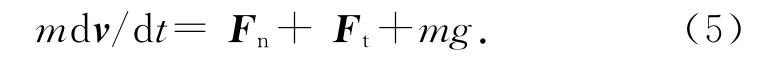
式中：m为颗粒质量，Fn和Ft分别为颗粒碰撞时受到的法向作用力和切向作用力.颗粒与床底之间、颗粒与颗粒之间均为弹性碰撞，碰撞过程中的碰撞力采用Hertz-Mindlin无滑移接触模型［26］获得，计算的时间步长取1×10-6s，碰撞示意图如图1所示.法向力和切向力分别表示为

式中：α为法向重叠量，vij是颗粒i相对于颗粒j的速度，n为从颗粒i球心指向颗粒j球心的单位矢量，kn和cn分别为颗粒i的法向弹性系数和法向阻力系数；δ是接触点切向位移，vct是接触点的滑移速度，kt和ct分别为切向弹性系数和切向阻尼系数.当时，颗粒i发生滑动，切向力为

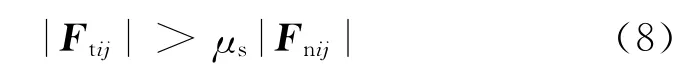
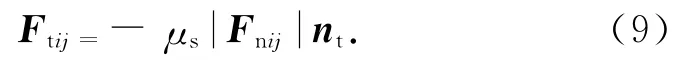
式中：μs为摩擦因数.弹性系数kn和cn的计算公式为

图1 颗粒间碰撞模型Fig.1 Collision model between grains

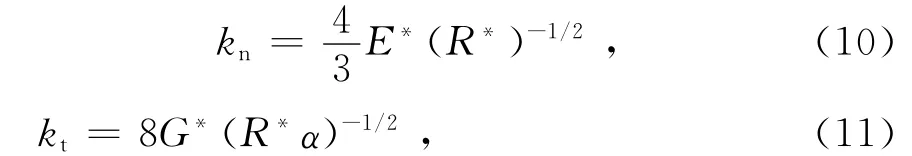
下标分别表示碰撞颗粒；E为弹性模量；G为剪切模量；e为弹性恢复系数.以上碰撞模型中，当i或j代表壁面（i，j=w）时，Rw趋于无穷大，R*=1，m*=1.颗粒与壁面的碰撞为完全弹性碰撞，egw=0且μgw=0.颗粒材料的物性参数为：泊松比γ=0.25，弹性模量E=108，剪切模量G=108，颗粒弹性恢复系数e=0.25，颗粒间摩擦系数μgg=0.9.

2 结果与讨论

2.1 单组分颗粒体系

将1 440个直径为12 mm，密度为1 000 kg／m3的圆形颗粒随机填充于计算区域内.对床底施加振动后，床内的颗粒将随之运动.振动一段时间至颗粒运动达到稳定状态，对颗粒的运动、动能分布以及能量耗散规律进行分析.高频振动时可能会产生湍流，如高频时会出现振动波和倍周期分叉现象.这些现象可能由间隙空气引起，但是具体机理目前还不明确.由于采用的颗粒直径较大（粒径为12 mm），空气曳力远小于颗粒惯性力，本研究忽略间隙空气的影响.

图2～5分别展示了振幅A为0.003 m，振动频率f为10 Hz和100 Hz时处于床内不同高度处内颗粒的运动.其中，v z（空心点曲线）和vχ（实心点曲线）分别为颗粒竖直方向和水平方向上的运动速度.在较低频率区，当f=10 Hz时，在竖直方向床层颗粒随着床底振动将周期性地上抛和下落，如图2和图3所示，vχ＜v z，床层整体仍然处于“有序”运动状态.而在高频区，当振动频率f=100 Hz时，如图4和图5所示，颗粒的运动规律性变差，vχ与v z大致相同.此外，沿床高方向上，低频和高频振动情况下颗粒的运动剧烈程度也存在明显差异.

图2 f=10 Hz且A=0.003 m时床内颗粒竖直方向的运动Fig.2 Vertical motion of grains in vibrated bed where vibration frequency is 10 Hz and amplitude is 0.003 m

图3 f=10 Hz且A=0.003 m时床内颗粒水平方向的运动Fig.3 Horizontal motion of grains in vibrated bed where vibration frequency is 10 Hz and amplitude is 0.003 m

由图可知，在低频率（f=10 Hz）区，床层上部颗粒运动幅度最大，颗粒运动的剧烈程度随着颗粒所处高度的增加而增加；而在高频（f=100 Hz）区，位于床底处颗粒的运动幅度大、运动最剧烈，沿着床层高度增大的方向颗粒的运动幅度逐渐减小.

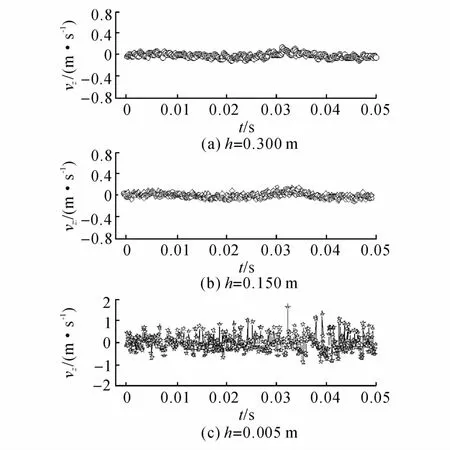
图4 f=100 Hz且A=0.003 m时床内颗粒竖直方向的运动Fig.4 Vertical motion of grains in vibrated bed where vibration frequency is 100 Hz and amplitude is 0.003 m

图5 f=100 Hz且A=0.003 m时床内颗粒水平方向的运动Fig.5 Horizontal motion of grains in vibrated bed where vibration frequency is 100 Hz and amplitude is 0.003 m

当床层稳定后，统计一定时间（6 s）内颗粒的平均动能（Ek），即可得到床内颗粒的动能分布情况.图6为不同振动条件下颗粒在振动床内的动能分布规律.当f=10 Hz时，如图6（a）所示，在振幅较小的情况下，颗粒动能（Ek）随着床内高度（h）的增加而增加；而随着振幅的进一步增大，颗粒动能随着高度不再是单调变化，即在床底和床层上部颗粒的动能较高，而在床层中部颗粒的动能相对较低.当f=100 Hz时，如图6（b）所示，在不同的振幅条件下，颗粒动能呈现出相同的变化趋势.颗粒动能随着高度的增加而单调减小，且随着振幅的增加，颗粒动能越来越大.

图6 不同振动参数下振动床内颗粒动能的分布规律Fig.6 Kinetic energy distribution in vibrated bed with different vibration parameters

颗粒间的弹性恢复系数e是影响床层能量分布规律的重要因素.图7为f=10 Hz且A=0.010 m时不同弹性恢复系数下颗粒床层的动能分布.随着e的增大，颗粒体系的总动能逐渐增大.当e＜0.75时，颗粒体系动能沿着床高（h）方向有着几乎一致的分布规律：颗粒动能在床层中部较低，而在床底和床层上部较高.当e=0.95时，颗粒体系动能分布有所改变，沿着床高增大的方向颗粒动能逐渐增大.

当床层振动时，颗粒之间产生频繁的相互碰撞，颗粒碰撞前后存在动能差这一动能差即为每次碰撞引起的动能耗散.将单位时间单位体积内床层颗粒碰撞的总能量耗散定义为床层的能量耗散速率，即.图8为不同振动参数下颗粒的能量耗散分布规律，其中γ*=γ／γav，γav为整个床层的平均能量耗散速率.

图7 不同弹性恢复系数下振动床内颗粒动能的分布规律Fig.7 Kinetic energy distribution in vibrated bed with different coefficients of restitution

当Γ＜1时，振动过程中床内颗粒未完全脱离床底，即颗粒与床底一起作上下运动，床层内各个高度动能耗散基本一致，如图8中实心圆点所示；而当无量纲振动强度增加（频率增加或振幅增加）后，系统中能量耗散梯度呈负梯度，即床底能量耗散远多于床层上部.高频率和大振幅床层中能量耗散均沿着床高的增加而减小，然而在量值上却存在差异.高频率时床底与床层上部能量耗散差异大，而高振幅时差异小.当为大振幅振动时，由于单位时间内的碰撞次数较高频振动时少，整个床层由于碰撞引起的能量耗散差异不大；而振动为高频率时，床底颗粒剧烈运动、床层上部颗粒运动幅度相对较小，床底能量耗散速率远大于上部床层.

如图8所示，随着f或A的增加，颗粒体系的平均能量耗散速率（γav）亦随之增加.这与文献［27］中的模拟和文献［28］中的实验研究结果有着一致的变化趋势：当无量纲振动强度一定，在f＜100 Hz时，随着f的增大，床层的平均能量耗散功率（耗散能量）逐渐增大.彭政等［28］根据能量守恒，将颗粒系统的平均能量耗散功率视作振动台向颗粒床进行能量传递的平均功率W（忽略空气的影响）.当振幅一定而频率增大时，振动变得更加剧烈，床底向床层输入的总能量增加.相应地，床层内颗粒间的非弹性碰撞次数增加，体系的能量耗散随之增大.

2.2 双组分颗粒体系

将2种密度相同尺寸不同的颗粒（大颗粒：直径为12 mm，密度为1 000 kg／m3，数量为720颗；小颗粒：直径为8 mm，密度为1 000 kg／m3，数量为2 430颗，大小颗粒总体积之比1：1）先后初始化于床层中，得到2种不同的分布形式.“巴西果”分布（BN distribution），床层下部为小颗粒、上部为大颗粒；“反巴西果”分布（RBN distribution），床层下部为大颗粒，上部为小颗粒.对颗粒床层施加竖直方向振动，在不同的振动条件下，统计一定时间（6 s）内颗粒的平均动能Ek.在统计时间段内，颗粒体系基本保持初始分布，统计过程中并不涉及颗粒分布状态的改变.图9为双组分颗粒处于不同分布时的动能分布规律.通过比较，可以得到以下结论.

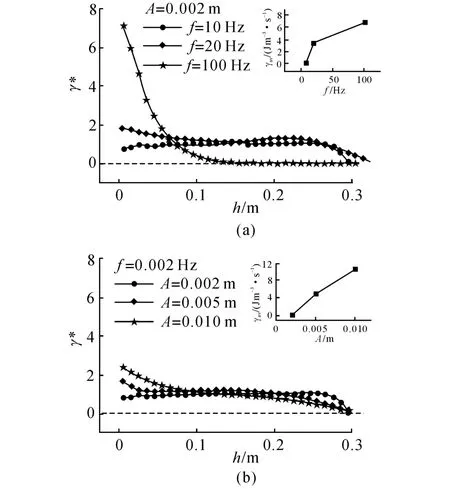
图8 床层内能量耗散速率分布Fig.8 Distribution of energy dissipation rate in granular bed

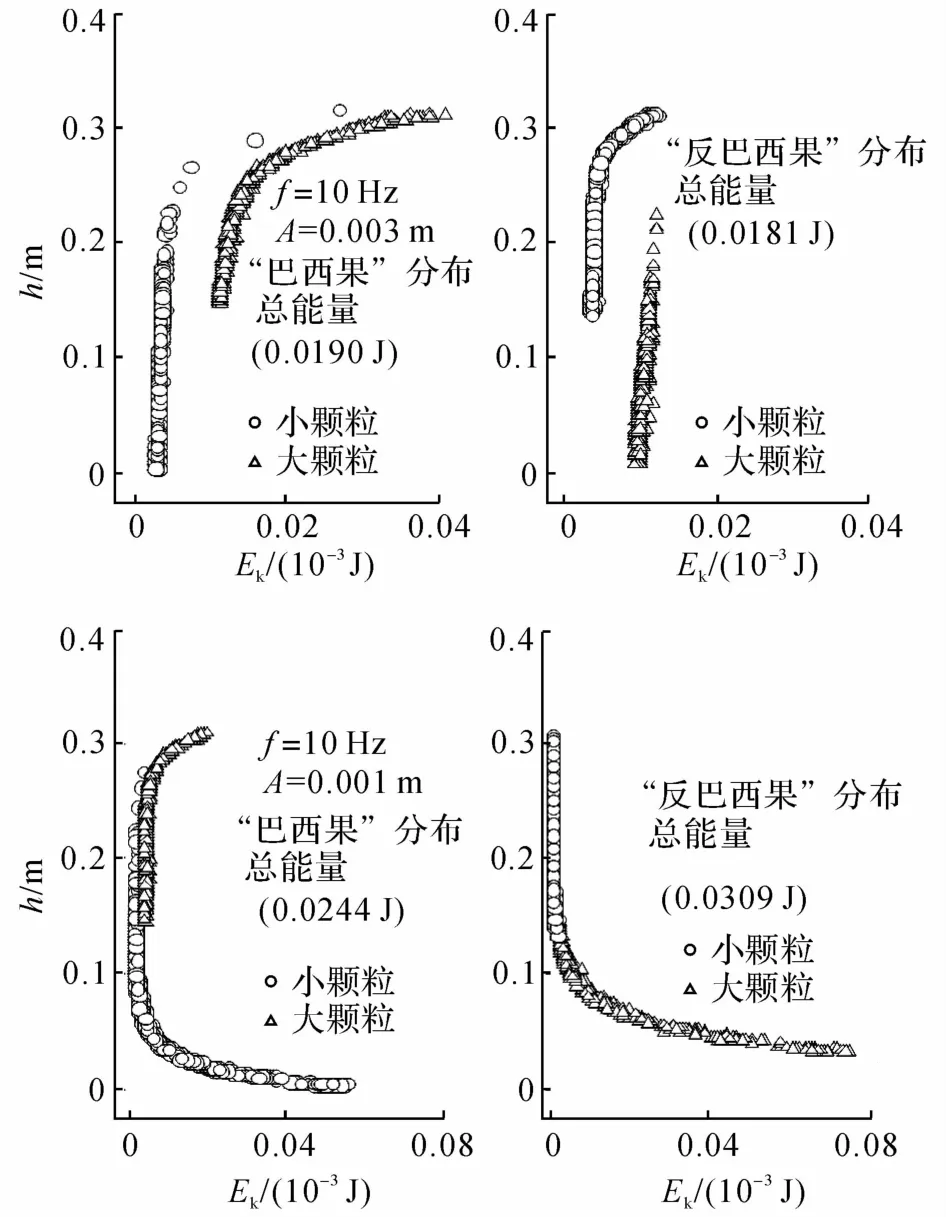
图9 双组分颗粒振动床内动能分布Fig.9 Kinetic energy distribution in binary granular mixture

1）相同位置大颗粒动能大于小颗粒动能；

2）当为低频率（f=10 Hz）振动时，同一组分颗粒动能沿床高方向上为正梯度分布，即颗粒动能随高度的增加而增加.当振动为高频率（f=100 Hz）时，同一组分颗粒动能沿床高方向上为负梯度，即颗粒动能随高度的增加而降低.

3）双组分颗粒分布不同时，床层内颗粒的动能分布形式存在显著差异，床层颗粒总动能也不相同.当低频振动时，“反巴西果”分布时床层颗粒总动能更低；当高频振动时，“巴西果”分布时床层颗粒总动能更低.

改变振幅与频率，比较“巴西果”和“反巴西果”2种不同分布时系统的动能（分别为BN分布总能量EBN和RBN分布总能量ERBN），可得到图10所示的相图.在A区域，Γ＜1，颗粒运动不会离开床层，在B区域（低频率、小振幅），当颗粒处于反巴西果分布时，颗粒床层的动能更低，ERBN＜EBN；在C区域（高频率、大振幅），当颗粒处于巴西果分布时床层动能更低，EBN＜ERBN.模拟得到2种分布情况下的系统总能量，总能量越低其分布越稳定，按照模拟结果进行分区.A区和B区的划分条件为Γ=1，因此，A区和B区分界线（见图10中虚线）的数学表达式即为A=g／（4π2f2）.通过非线性多项式拟合，可以得到B区和C区的分界线（见图8中实线）的表达式为

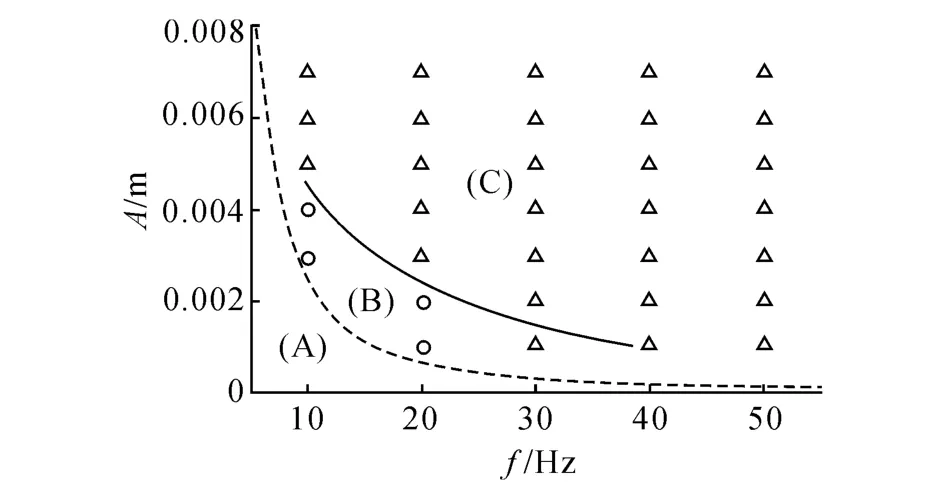
图10 颗粒分布对床层动能的影响Fig.10 Effect of grain size distribution on kinetic energy

颗粒直径越小，单位体积内颗粒数量越多，相同条件下碰撞次数越多，因此，相比于大颗粒床层而言，小颗粒床层对外部输入能量具有更强的耗散能力.沿床层床高方向颗粒动能分布不同，存在颗粒动能相对更大的“高动能区”.当耗散能量强的小颗粒处于床层“高动能区”时，整个床层对外界输入能量具有更强的耗散能力，使得整个床层自身动能更低.

对于低频率及低振幅振动，床层“高动能区”处于床层上部，因此双组分颗粒处于“反巴西果”分布时床层总动能更低；而对于高频率振动，床层“高动能区”处于床底，双组分颗粒处于“巴西果”分布时床层总动能更低.

3 结论

（1）作为颗粒体系微观结构研究的有效工具，离散单元法可以有效地用于颗粒体系的能量传递与耗散的模拟研究中.结果表明：当振动参数（振幅和频率）发生改变时，沿着床层的高度方向颗粒的能量分布、传递与耗散随之发生改变.低频振动时，碰撞引起的能量耗散沿床高方向逐渐增加；高频振动时，沿床高方向颗粒运动引起的能量耗散迅速减小.

（2）双组分颗粒放入振动床层中，系统的总动能随着振动频率及振幅的增加而增大.同时，双组分颗粒在床内的分布也会影响床层总动能：在低振幅、低频率时，“反巴西果”分布时床层总动能较低，反之则“巴西果”分布时床层总动能较低.

（3）颗粒系统为自身动能分布满足某一条件极值（例如：总能量最低），而调整床层内双组分颗粒的分布，最终处于稳定的分离状态.“巴西果”分布和“反巴西果”分布时床层具有的总动能差异是否为颗粒分离的原始驱动力，或与颗粒分离的驱动力之间存在何种联系，有待进一步研究.

（

）:

［1］JAEGER H M，NAGEL S R，BEHRINGER R P.Granular solids，liquids，and gases［J］.Reviews of Modern Physics，1996，68：1259- 1273.

［2］KUANG S B，YU A B，ZOU Z S.Computational study of flow regimes in vertical pneumatic conveying［J］.Industrial and Engineering Chemistry Research，2009，48：6846- 6858.

［3］鲍德松，张训生.颗粒物质与颗粒流［J］.浙江大学学报：理学版，2003，30（5）：514- 517.BAO De-song，ZHANG Xun-sheng.Granular matter and granular flow［J］.Journal of Zhejiang University：Science Edition，2003，30（5）：514- 517.

［4］陆坤权，刘寄星.颗粒物质［J］.物理，2004，33（9）：629- 635.LU Kun-quan，LIU Ji-xing.Granular matter［J］.Physics，2004，33（9）：629- 635.

［5］刘伟伟，卢春喜，范怡平，等.气固流化床中双组分混合颗粒的流态化特性［J］.化工学报，2008，59（8）：1971- 1978.LIU Wei-wei，LU Chun-xi，FAN Yi-ping，et al.Flow behavior of binary mixture particles in gas-solid fluidized beds［J］.Journal of Chemical Industry and Engineering，2008，59（8）：1971- 1978.

［6］张树青，卢春喜，时铭显，等.气固流化床中大差异双组份颗粒分级特性的实验研究［J］.高校化学工程学报，2004，55（10）：1581- 1592.ZHANG Shu-qing，LU Chun-xi，SHI Ming-xian，et al.Segregation of binary particle with significant size difference in gas-solid fluidized beds［J］.Journal of Chemical Engineering of Chinese Universities，2004，55（10）：1581- 1592.

［7］江茂强，赵永志，郑津洋.非等密度颗粒气固流化床的微观尺度模拟与分析［J］.浙江大学学报：工学版，2009，43（9）：1703- 1708.JIANG Mao-qiang，ZHAO Yong-zhi，ZHENG Jinyang.Micro-scale simulation and analysis of gas-solid fluidized bed with multi-density distribution of particles［J］.Journal of Zhejiang University：Engineering Science，2009，43（9）：1703- 1708.

［8］DEEN N G，WILLEM G，SANDER G，et al.Numerical analysis of solids mixing in pressurized fluidized beds［J］.Industrial and Engineering Chemistry Research，2010，49：5246- 5253.

［9］KHAIN E，MEERSON B.Onset of thermal convection in a horizontal layer of granular gas［J］.Physical Review E，2003，67：021306.

［10］HSIAU S S，WU M H，CHEN C H.Arching phenomena in a vibrated granular bed ［J］.Powder Technology，1998，99：185- 193.

［11］AOKI K M，AKIYAMA T.Spontaneous wave pattern formation in vibrated granular materials［J］.Physical Review Letters，1996，77：4166- 4419.

［12］YUAN X，ZHENG N，SHI Q，et al.Segregation in mixtures of granular chains and spherical grains under vertical vibration［J］.Physical Review E，2013，87：042203.

［13］ROSATO A D，STRANDBURG K J，PRINZ F，et al.Why the Brazil nuts are on top：Size segregation of particulate matter by shaking ［J］.Physical Review Letters，1987，58：1038- 1040.

［14］HSIAU SS，CHEN W.Density effect of binary mixtures on the segregation process in a vertical shaker［J］.Advanced Powder Technology，2002，13：301- 315.

［15］SHINBORT T，MUZZIO F J.Reverse buoyancy in shaken granular beds［J］.Physical Review Letters，1998，81：4365- 4368.

［16］LIU C P，WANG L，WU P，et al.Effects of gas flow on granular size separation ［J］.Physical Review Letters，2010，104：188001.

［17］ROSATO A D，BLACKMORE D L，ZHANG N，et al.A perspective on vibration-induced size segregation of granular materials ［J］.Chemical Engineering Science，2002，57：265- 275.

［18］LIU C P，WANG L，WU P，et al.Size distribution in gas vibration bed and its application on grain drying［J］.Powder Technology，2012，221：192- 198.

［19］林建忠，游振江，石兴.混合层中柱状粒子运动的研究［J］.工程热物理学报，2003，24（6）：972- 975.LIN Jian-zhong，YOU Zhen-jiang，SHI Xing.Research on the motion of cylindrical particle in mixing layer［J］.Journal of Engineering Thermophysics，2003，24（6）：972- 975.

［20］张国华，孙其诚，黄芳芳，等.摩擦颗粒体系各向同性压缩过程中的堵塞行为［J］.物理学报，2011，60（12）：124502.Zh ANG Guo-hua，SUN Qi-cheng，HUANG Fangfang，et al.Jamming phenomena of a two-dimensional frictional granular system under isotropic confining［J］.Acta Physica Sinica，2011，60（12）：124502.

［21］吴锦坤，罗坤，胡桂林，等.鼓泡流化床流动特性的直接数值模拟［J］.浙江大学学报：工学版，2007，41（3）：504- 508.WU Jin-kun，LUO Kun，HU Gui-lin，et al.Direct particle simulation of flow characteristics in bubbling fluidized bed［J］.Journal of Zhejiang University：Engineering Science，2007，41（3）：504- 508.

［22］赵永志，程易，金涌.提升管与下行床颗粒团聚行为的离散颗粒模拟［J］.化工学报，2007，58（1）：44- 53.ZHAO Yong-zhi，CHENG Yi，JIN Yong.CFD-DEM simulation of clustering phenomena in riser and downer［J］.Journal of Chemical Industry and Engineering，2007，58（1）：44- 53.

［23］WILDMAN R D，HUNTLEY J M.Scaling exponents for energy transport and dissipation in binary vibro-fluidized granular beds［J］.Physics of Fluids，2003，15：3090- 3098.

［24］NARAYAN O，RAMASWAMY S.Anomalous heat conduction in one-dimensional momentum-conserving systems［J］.Physical Review Letters，2002，89：200601.

［25］DHAR A，SAITO K.Heat conduction in the disordered Fermi-Pasta-Ulam chain［J］.Physical Review E，2008，78：061136.

［26］MINDLIN R D.Compliance of elastic bodies in contact［J］.Journal of applied mechanics，1949，16：259- 268.

［27］YANAGIDA T，MATCHETT A J，COULTHARD J M.Dissipation energy of powder beds subject to vibration［J］.Chemical Engineering Research and Design，2001，79：655- 662.