量子密钥分配系统中非线性偏振耦合的研究
董颖娣,彭进业
(1.西北工业大学电子信息学院,西安710072;2.西安建筑科技大学信息与控制工程学院,西安710055)
引 言
自1984年量子密钥分发协议的提出及1992年量子密钥分发演示实验成功[1-2]以来,量子密钥分发系统已经从实验研究发展到商业应用[3]阶段,其相关的技术也相继成熟,但相位补偿技术和偏振控制技术[4]仍然是影响密钥分发系统性能的关键。
在量子密钥系统中,量子态以两个垂直的线偏振模的形式在光纤中传输,光纤传输性能影响系统的稳定性和安全性[5-7]。1986 年,WINFUL[8]指出了由于非线性耦合,将导致连续光偏振不稳定。MARCUSE等人研究了具有随机双折射的非线性偏振模色散,并将非线性耦合薛定谔方程转换为马尔科夫偏振模色散方程[9-10]。量子密钥系统中两偏振模耦合率下降即非线性偏振旋转会引起量子态偏振度随机抖动[11],从而使稳定的量子密钥分发变得困难,限制了偏振编码方案在量子保密通信中的应用和发展,以非线性耦合薛定谔方程分析两偏振模耦合率问题,并没有开展研究和讨论。本文中分析了非线性偏振耦合对连续变量量子密钥分发(quantum key distribution,QKD)系统的影响,并提出了以非线性偏振耦合反馈控制技术改善系统性能,并给出了实验方案。
作者以非线性薛定谔方程阐述了光纤非线性偏振耦合;在非线性偏振耦合条件下分析连续变量量子密钥分配系统中的性能;采用香农信息论分析了合法通信双方之间的互信息;给出了非线性偏振耦合反馈的控制理论算法和实验方案。
1 原理和模型
近年来,量子密钥分配系统向高速化、实用化方向发展,对于速率在100Gbit/s以上的量子密钥分配实用系统,偏振复用[12]是系统关键。由于非线性偏振耦合使两个偏振方向独立的调制信号偏振复用后抖动增加,非线性偏振耦合过程采用光纤的非线性薛定谔方程[13]描述:
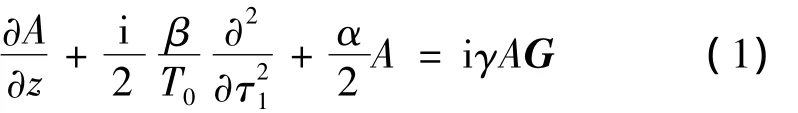
式中,A为复振幅,z为传输距离,β为传输常数,T0为脉冲宽度,τ1为传输时间,α为光纤损耗系数,γ为光纤非线性系数,G为2×2耦合矩阵,其决定光纤内的非线性旋转,计算公式如下所示:

式中,Ax,Ay分别为量子信号和本振信号的复振幅,Δφ为两者相位差。在量子密钥分配系统中,两路参与信号是不断变化的,当本振信号与量子信号由于非线性偏振旋转发生变化时,即造成偏振复用信号抖动增加,从而影响使密钥分发系统的传输性能下降。
1.1 量子密钥系统的非线性偏振旋转分析
量子密钥分发系统偏振复用过程如图1所示。量子密钥系统的两路信号,量子信号和本振信号,在进入光纤前进行偏振复用,形成偏振态垂直的复用信号,在普通低双折射的单模光纤中,只考虑非线性偏振效应而忽略本征色散影响(假定本征色散已经被补偿)时,光纤中的圆偏振态将保持不变,仅产生相移。

Fig.1 Principle scheme of polarization multiplexing in a quantum key distribution system(LD:laser device;PBS:polarization beam splitter;BS:beam splitter;PD:pilot detector)
在偏振分束器PBS1处,相互垂直的线偏振光与圆偏振态之间的关系为:
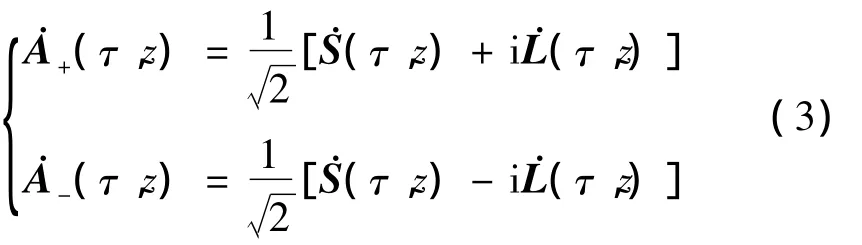
式中,˙A+(τ,z),˙A-(τ,z)分别表示两个圆偏振光的复振幅向量,˙S(τ,z),˙L(τ,z)分别表示量子密钥分配系统的线偏振态的信号光和本振光。圆偏振态传输距离至PBS2处,其偏振态保持不变,其非线性偏振旋转产生复振幅相位与光纤非线性之间关系[14]可用下式来描述:
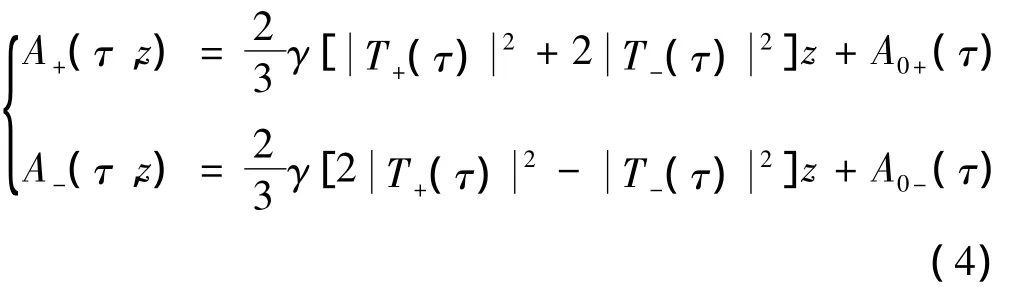
(2)细煤泥系统处理能力不足。煤质较好时,压滤机一个压滤循环周期需11 min,5台压滤机处理能力105 t/h;煤质差时,泥化现象严重,小于320目粒级物料高达67.25%,煤泥沉降极慢,压滤机一个压滤循环周期需23 min以上,6台压滤机处理能力只有60 t/h,而且滤饼水分较高。按年入洗500万t原煤计算,每小时需处理的细煤泥量为109 t,所以压滤机处理能力明显不足,这是洗水浓度居高不下的主要原因。
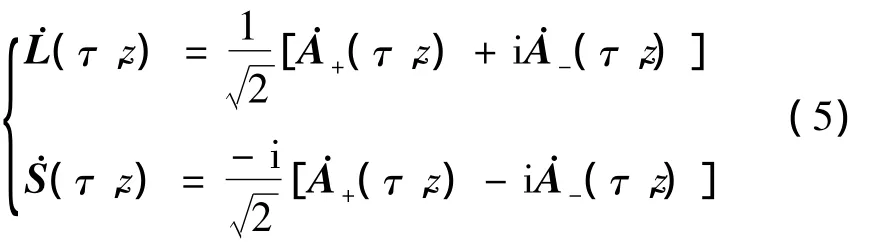
经过推导后,在PBS2信号与PBS1处信号之间的关系用偏振矩阵描述,如下式所示:
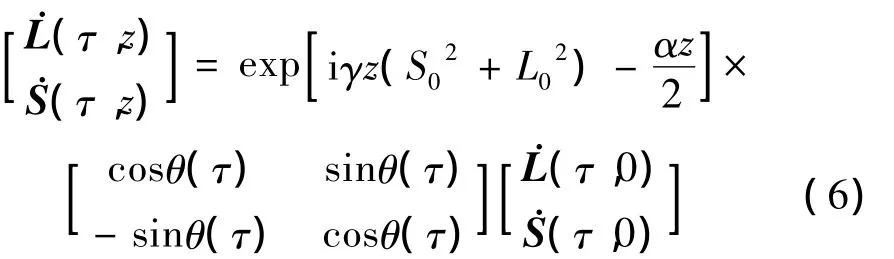
1.2 量子密钥系统的非线性偏振旋转分析
量子密钥分配系统偏振复用信号经过光纤长距离传输后,因光纤非线性作用,其偏振方向与分束器的偏振方向发生分离,如图2所示。
由于光纤的非线性效应影响,本振光偏振态与水平轴产生了角度为θ(τ)的偏转。根据马吕斯定律,通过偏振分束器后,本振光在水平方向的强度分量为ILO×cos2θ(τ),信号光在垂直方向的偏振分量为 IQSsin2θ(τ)。根据偏振失配原理,本振光在垂直方向的分量大小即为引起系统误比特率的附加噪声。当信源符号为X、输出Y为高斯分布时,通信双方之间互信息量可用香农定理描述。在此定义带宽 B=1Mbit,σx2/n0
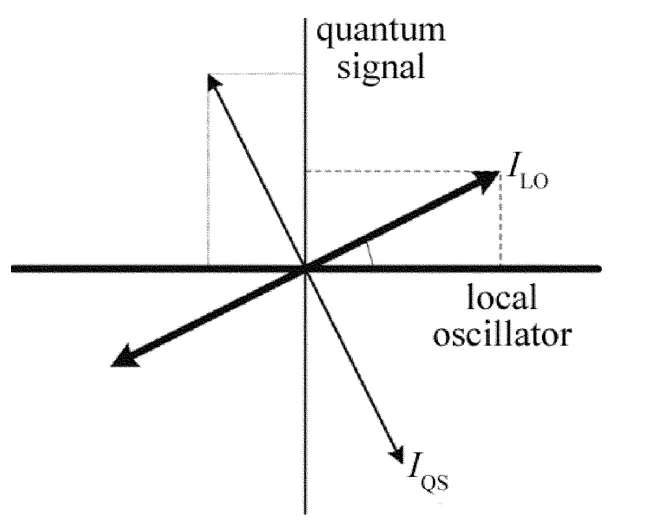
Fig.2 Sketch diagram of nonlinear polarization after rotating(ILO:optical field of local oscillator;IQS:optical field of quantum signal)
2为量子信号的信噪比和分别量子信号及高斯噪声的概率密度分布函数方差。当非线性偏振旋转角为θ(τ)时,信源分布函数为 X-N(0,σx2cos2θ(τ)),噪声分布函数为 Y-N(0,n02(1+sin2θ(τ))),由此可知传输系统的非线性偏振旋转后密钥分配系统信息容量为:

由于非线性偏转旋转角θ(τ)使系统互信息量下降程度如图3所示。
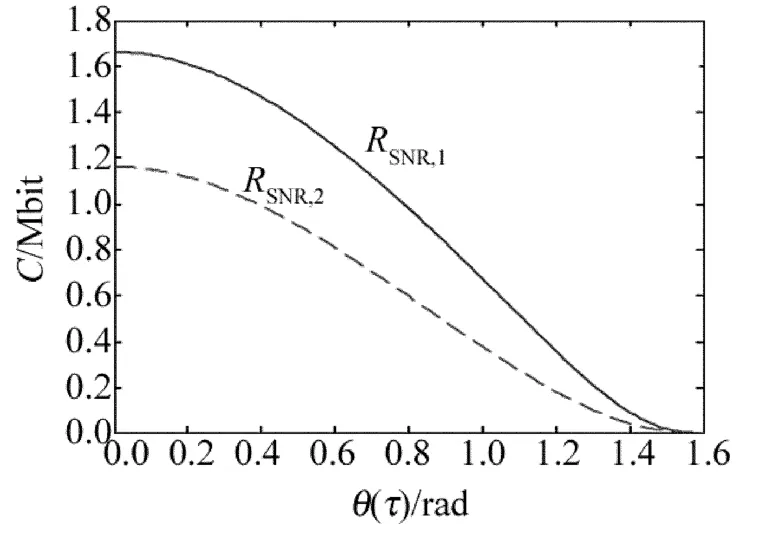
Fig.3 Relationship between nonlinear polarization rotating angle θ(τ)and transmission capacity C
在此设计传输光纤长度为20km条件下,光纤非线性系数为2.2/km、损耗系数为0.2dB/km时,本振光与信号光的初始相位差π/2、本振光与信号光比值为9∶1、信号服从均值为0、方差为20的高斯分布,量子密钥分配系统的信道传输率与非线性偏振旋转角之间关系如图3所示,信噪比1(RSRN,1)设置为9,信噪比2(RSRN,2)设置为4,由图3可知,随着非线性偏振旋转角θ(τ)逐渐增加,传输信道的信息容量C下降,当非线性偏振旋转角增至1.58左右时,传输容量下降为0。
由此可见,在量子密钥分配系统由于非线性偏振旋转角增加了信道的偏振抖动程度,从而引起量子密钥系统信息容量下降;抖动越剧烈,系统传输效率越低,这一问题成为制约量子密钥系统稳定工作的瓶颈。
2 非线性偏振耦合反馈控制技术方案
2.1 非线性偏振耦合反馈控制的理论分析
以最大似然估计法计算非线性偏振耦合的均值〈θ(τ)〉:
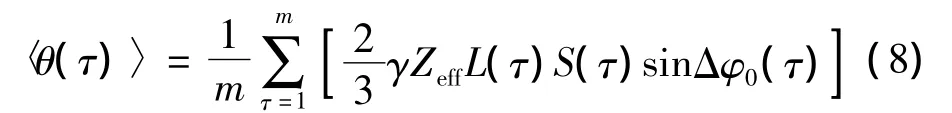
其补偿角大小Δθ(τ)为:
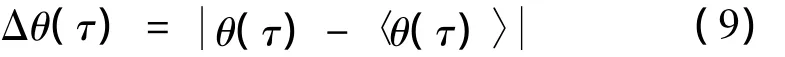
式中,m采样时间的极值,τ为系统采样时间内采样参量。经过反馈补偿后系统接收端偏振控制器的传输矩阵可以描述为:
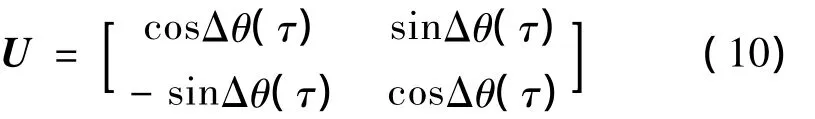
接收端量子偏振态为:
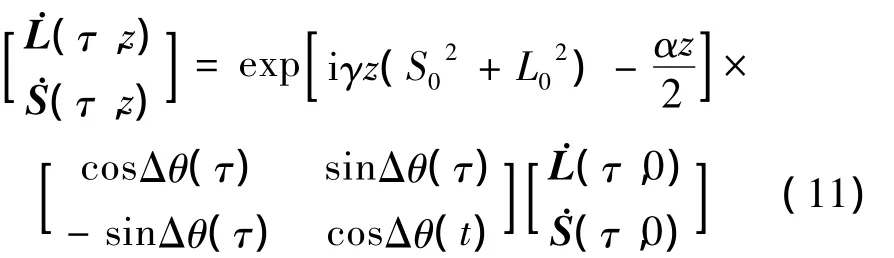
由(9)式可知,通过反馈补偿后量子密钥分配系统的信息容量为:
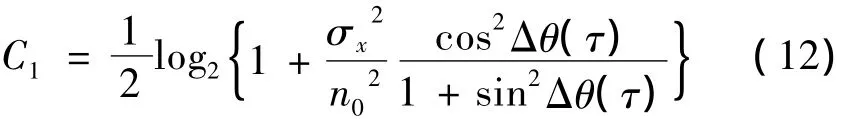
与图3相同条件下,仿真结果如图4所示,经过反馈补偿后,非线性偏振耦合值变化范围逐渐缩小至0~0.8,说明量子密钥分配系统中量子态的抖动幅值下降,信道传输容量变化量逐渐变小,以信噪比1为例,经过非线性偏振反馈补偿后,随着修正后的非线性偏振旋转角Δθ(τ)增加,传输容量C1由1.62下降至1.00,下降的抖动程度小于没有补偿的系统的传输性能,且系统的传输容量比没有进行反馈补偿条件下提高了61%。

Fig.4 Relationship between nonlinear polarization rotating angle Δθ(τ)and transmission capacity C1after amendment
2.2 非线性偏振反馈矫正的实验方案分析
量子密钥系统非线性偏振反馈控制如图5所示,其中反馈控制部分用分束器将本振光按照50∶50比例分束,经检测器转化为电流,计算得到其幅值大小为(幅值通过计算的机采样获取),计算采样点的均值,将计算均值作为矫正依据,对系统的非线性偏振耦合偏振角进行及时矫正,以改善系统的稳定性。
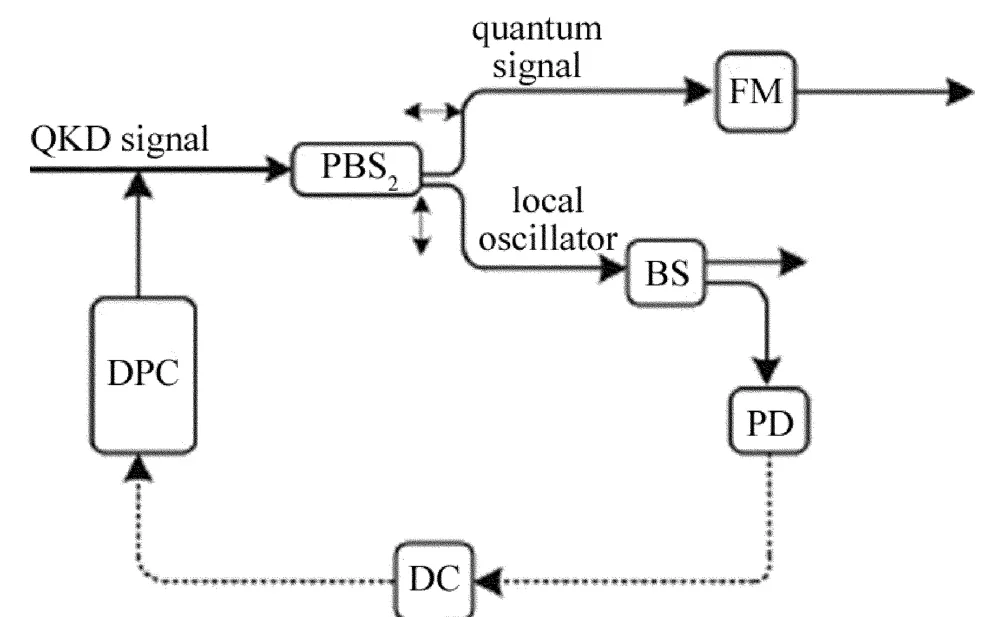
Fig.5 Sketch diagram of feedback control of nonlinear polarization in quantum key distribution(FM:Faraday mirror;DC:dynamic controller;DPC:dynamic polarization controler)
反馈控制的具体实施过程通过以下两个阶段完成。
2.2.1 分光检测阶段 量子密钥分发的接收方将量子信号通过偏振分束器,根据光的偏振理论及偏振耦合器的性质,如果偏振无漂移,那么本振光将会和信号光完全分开。在存在偏振漂移的情况下,本振光会泄露一部分光到信号光端,使得本振光自身的能量降低,通过分出一部分本振光来进行检测,可以得知偏振漂移程度。在偏振匹配的情况下,本振光的强度达到最大。此时即为无偏振的状态。在此电流检测之前需要直流转换器将其转化为直流信号,并将其放大,以保证检测准确性。
2.2.2 非线性偏振矫正阶段 反馈控制电路将输出的直流电压反馈给接收方的动态偏振控制器内的单片机,单片机对反馈电压进行采样,并通过下述反馈控制算法来持续调节动态控制器,使得直流反馈电压最大。动态控制器[15]通过改变其内部的4个光纤挤压器上的电压 V1,V2,V3,V4对偏振复用信号的偏振态进行控制,电压调节范围从-12V到+12V之间。光的偏振态用邦加球上的点来描述,斯托克斯参量S1,S2,S3对应着邦加球相应的坐标轴。倘若改变电压V1或V3,则偏振态会在邦加球上以S1为中心转动;改变电压V2或V4,则偏振态会在邦加球上以S2为中心转动。基于以上讨论,偏振反馈算法的具体流程如下:(1)动态偏振控制器的单片机对直流反馈电压采样并记录数据;(2)4个控制电压都置为0V,选择第1个控制电压;(3)根据均值电流大小增加电压,此时偏振态会在邦加球上绕着对的矢量轴做顺时针转动,采集直流反馈电压,如果电压已经达到了+12V,进入步骤(7);(4)根据均值电流大小增加电压,此时偏振态会在邦加球上绕着对应的量轴做顺时针转动,采集直流反馈电压,如果电压已经达到了+12V,进入步骤(7);(5)根据均值电流大小减小电压,此时偏振态会在邦加球上绕着对应矢量轴做逆时针转动,采集直流反馈电压,如果电压已经达到了-12V,进入步骤(7);(6)如果直流反馈电压增大,那么继续步骤(5)否则,进入步骤(7);(7)选择下一个电压控制器,继续步骤(3)。
可以将直流反馈电压一直保持在一个最大值的状态。根据以上分析,这时对应的本振光的强度最强,本振光没有发生泄漏,偏振复用信号与偏振分束器之间没有偏振旋转,信号光与本振光之间的非线性偏振效应可以得到相应的改善。
3 结论
偏振编码方案在量子保密通信中有着广泛的应用,非线性偏振耦合将引起偏振复用信号的偏振抖动增加,从而降低了量子密钥分配系统的安全性和稳定性。量子密钥系统非线性偏振耦合导致偏振复用信道抖动增加,将偏振控制的思想运用于量子密钥分发系统的非线性偏振耦合,通过对非线性偏振偏移量监测提供反馈电压,补偿了由于偏振随机抖动引起的偏振漂移。数值仿真表明,系统经过反馈后,量子态偏振抖动度下降,量子密钥分配系统的传输效率增强,系统稳定性得以改善,从而实现了基于偏振编码的长距离高稳定性的量子密钥分发实验。
[1] BENNETT C H,BRASSARD G.Quantum cryptography:public key distribution and coin tossing[C]//Computer Systems and Signal Processing,Proceedings of IEEE International Conference and Signal Processing.New York,USA:IEEE,1984:175-179.
[2] EKERT A K.Quantum cryptography based on bell’s theorem[J].Physical Review Letters,1991,67(6):661-663.
[3] JOUGUET P,KUNZ-JACQUES S,LEVERRIER A,et al.Experimental demonstration of long distance continuous-variable quantum key distribution[J].Nature Photonics,2013,7(5):378-381.
[4] CHEN J,LI Y,WU G,et al.Stable quantum key distribution with polarization control[J].Physica Sinica,2007,56(9):5243-5246(in Chinese).
[5] JOUGUET P,KUNZ-JACQUES S,DIAMANTI E.Preventing calibration attacks on the local oscillator in continuous-variable quantum key distribution[J].Physical Review,2013,A87(9):2313-2317.
[6] LEVERRIER A,GRANGIER P.Long distance quantum key distribution with continuous variables[M].Madrid,Spain:Theory of Quantum Computation,Communication,and Cryptography,2014:143-152.
[7] HAN B B,PEI Ch X,CHEN N,et al.Analysis of the effect of polarization mode dispersion on QKD[J].Journal of Xidian University,2008,35(5):830-833(in Chinese).
[8] WINFUL H G.Polarization instabilities in birefringent nonlinear media:application to fiber-optic devices[J].Optics Letters,1986,11(1):33-35.
[9] MARCUSE D,MANYUK C R,WAI P K A.Application of the Manakov-PMD equation to studies of signal propagation in optical fibers with randomly varying birefringence [J].IEEE Journal of Lightwave Technology,1997,15(9):1735-1746.
[10] MARCUSE D.Derivation of analytical expressions for the bit-error probability in lightwave systems with optical amplifiers[J].IEEE Journal of Lightwave Technology,1990,8(12):1816-1823.
[11] WANG J,MIAO H L.Compensation of polarization mode dispersion by in-line synchronous modulation [J].Laser Technology,2002,26(3):211-213(in Chinese).
[12] FOURSA D,CAI Y,CAI J X,et al.Coherent 40Gbit/s transmission with high spectral efficiency over transpacific distance[C]//OSA Library Resource Center.Los Angeles,USA:OSA Library Resouke Center,2011:657-672.
[13] AGRAWAL G.Applications on nonlinear fiber optics[M].2rd ed.Pittsburgh,USA:Academic Press,2013:468-470.
[14] LIU L L,WU Ch Q.Investigation on decreasing of DOP in PM systems caused by nonlinear polarization coupling in fibers[J].Journal of Beijing Jiaotong University,2013,37(6):118-201(in Chinese).
[15] FANG J.Continuous-variable quantum key distribution:optical system design and improved schemes[D].Shanghai:Shanghai Jiaotong University,2014:48-50(in Chinese).

