Ag线栅能带结构的有限时域差分法计算

张　青,赵小童,米佳佳,查射曦,石建平

Ag线栅能带结构的有限时域差分法计算

张青,赵小童,米佳佳,查射曦,石建平

摘要:Ag线栅具有超强的透射特性，色散能带结构的精确计算有助于分析理解亚波长结构中的电磁特性。利用有限时域差分法FDTD计算了亚波长Ag线栅能带结构，并根据该方法计算了周期为500nm的Ag光栅在不同厚度情况下的能带结构图。结果表明从该方法计算出来的能带结构中可以分析得到Wood异常、波导模式、SPP模式以及透射共振波长红移等多种电磁现象，与现有文献的理论分析一致。

关键词:亚波长Ag线栅; 能带结构;表面等离激元SPP；有限时域差分法FDTD

1引言

亚波长金属线栅是指光栅周期远小于波长的一维金属光栅。这种光栅具有超强的透射特性，在光场局域、微腔量子电动力学、高密度数据存储、近场光学等领域具有巨大的应用潜力。然而，对于亚波长金属线栅的电磁特性的解释目前还没有定论，主要有两种观点。一种观点认为是金属膜表面等离子体激元的共振激发和耦合导致了这种透射增强效应，称为SP模式[1,2]；另一种观点认为类Fabry- Perot( F -P) 腔的作用才是产生这种现象的原因[3,4]。但这两种观点都不能完美解释光栅透射峰的红移现象，以及介质基底对光栅透射峰的影响，这给器件设计带来了一定的困扰。

因此近年来人们开始从色散曲线和能带结构来直接解释亚波长结构中的电磁现象。根据色散曲线和能带结构可以计算得到很多非常重要的电磁特性参数，比如SP波长、传播距离、透射光谱、透射强度等等，为器件设计提供了理论指导。为了获得一维Ag薄膜光栅的能带色散图，Porto[5]等人使用简化模型来计算能带结构图。假定狭缝的垂直表面为完美金属并仅考虑电磁场的基态，通过改变入射角计算得到光子能带结构图ω(kx)。不过，这种简化模型得到的能带图尚不能完全准确的给出透射峰位置。本文提出采用FDTD算法来计算一维亚波长光栅能带结构的方法，不采用近似条件，可以准确的得到能带结构图。

2能带结构关系的计算方案

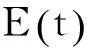
为保证偶极子源能够激发所有的电磁模式，偶极子的位置需要随机分布。偶极子位相偏移与位置和波矢有关:

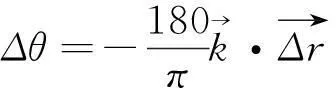
(1)

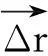
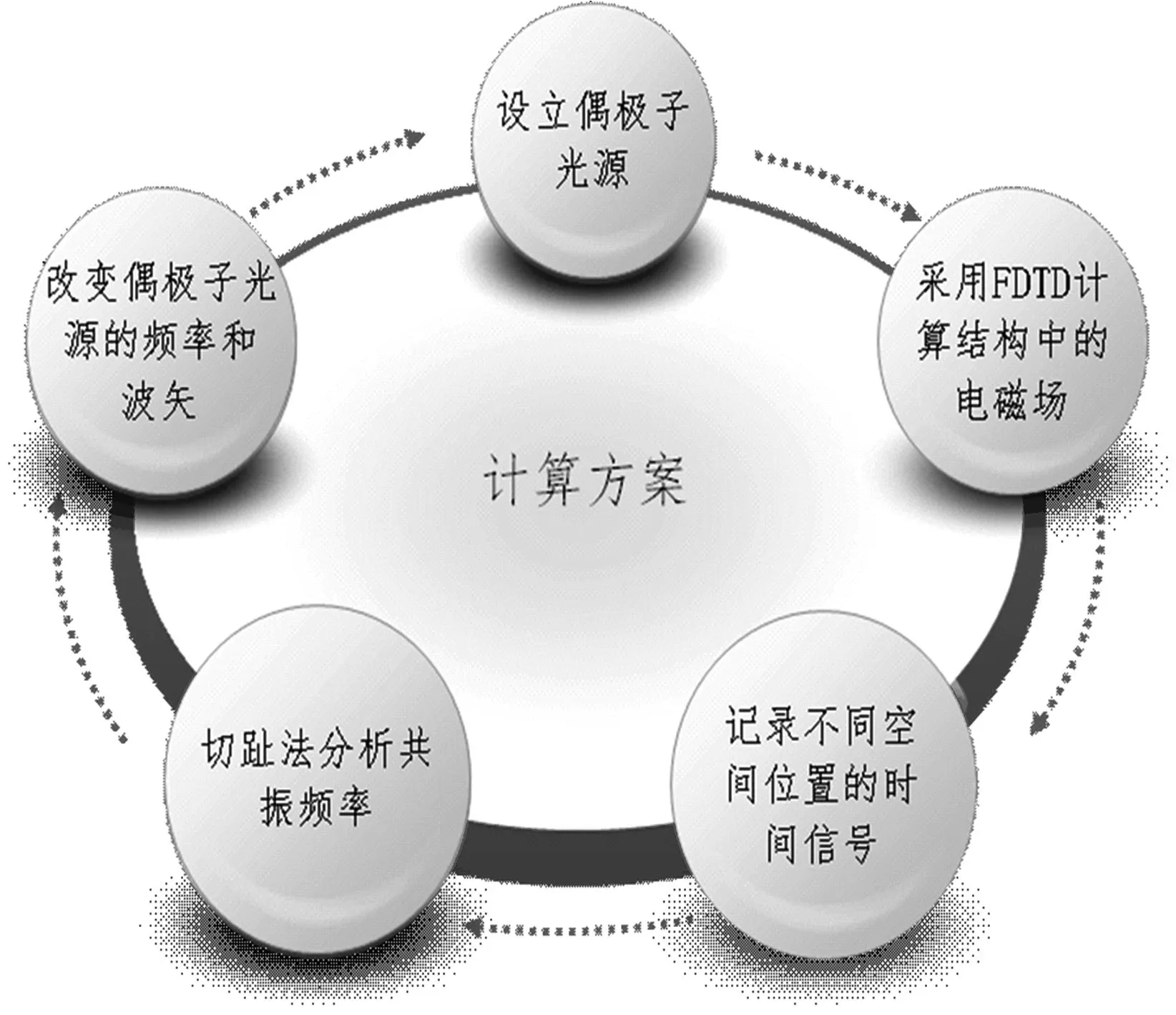
图1　计算方案

电磁场计算采用时域有限差分法FDTD[6]来完成，仿真模型如图2所示。在计算区域上下边界采用完美匹配层PML作为吸收边界，在光栅周期方向采用Bloch边界条件。计算区域的网格内每个光栅周期结构包含了30个网格。

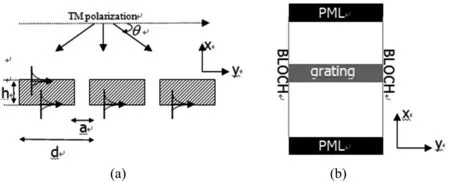
图2　(a)亚波长光栅结构示意图，(b)时域有限差分方法计算区域

3Ag薄膜一维光栅色散能带计算与分析

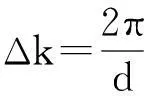
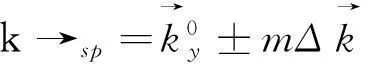
(2)

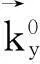
采用上述计算方案，计算了周期500nm、占空比1:9的光栅厚度不同的能带色散图。入射光源TM极化，频率为0～900THZ(最小入射波长为333.33nm),光栅厚度分别为50nm、300nm、600nm和800nm。光栅材料选择Ag，可以更加明显的观察到透射增强效应，方便与现有文献的相关结论对比验证。

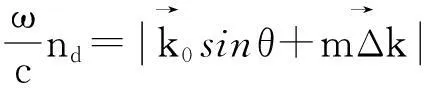
光栅厚度增加为300nm时计算的能带色散图,如图3(b)所示。在厚度较小时spp能带色散曲线紧贴着Rayleigh异常能带，厚度增加后出现了明显的带隙[5], 相对能量较小的能带，能量较大能带位置变化很小。垂直入射时的共振频率变为597THZ、510THZ，分别对应图中交点A和B; 在厚度增加到600nm的光栅能带色散图，如图2(c)中,随着光栅厚度的增加，交点B向低频波段移动，即共振波长向长波段移动(红移)，同时入射共振频率增多，出现了平坦波导模式的能带；厚度增加至800nm时光栅的能带，如图2(d)中，A和B两交点的高度差更大了，两个共振频率差值增大，共振波长的红移量随着厚度的增加而增加,出现了更多的平坦能带，垂直入射的共振频率点增多。

图3　周期500nm, 占空比1:9，厚度不同的 Ag光栅色散能带图(a)厚度50nm,(b)厚度300nm,(c)厚度600nm,(d)厚度800nm

通过以上分析发现厚光栅的能带色散图中除了spp共振模式还包含了波导模式，可以由式2Φ+k2h=m@π[10]来分析这些模式,h是光栅的厚度，k是模式的波矢，Φ是光栅的相位变化，m取整数。当金属光栅厚度h较小时，如图3所示，共振模式称为spp模式，且spp共振模式对入射角的变化很敏感。入射角改变为10°时，两个不同的频率都可以激发spp模式，如图4，透射光谱验证了这一特性。垂直入射时，如图4(a)，光栅透射光谱在共振频率值593THZ处出现了尖锐的峰。斜入射时，如图4(b)，透射光谱出现了两个明显的透射峰，对应的共振频率分别为509THZ和637THZ；当厚度h的继续增加，m与Φ保持不变，对应的K减小，spp较小的共振波长发生红移。TM波垂直入射到光栅上零级透射曲线如图5(a)所示，验证了透射峰与入射平面光频率的关系，厚度增加到100nm后，出现了一个波长略大于周期500nm的明显透射峰。这个透射峰随着光栅厚度的增加移动至低频区域，共振频率向低频段移动，共振波长红移，同时透射峰的半高宽度也增大了；当厚度h达到一定值后，已有的m值不能满足公式。因此m值增大，出现更多的共振波长，能带图中包含了spp模式能带和波导模式能带。如图5(b)所示，当光栅厚度增加为300nm时，透射光谱中出现了第三个峰，在0～900THZ频率段上包含了spp模式和波导模式的共振峰。

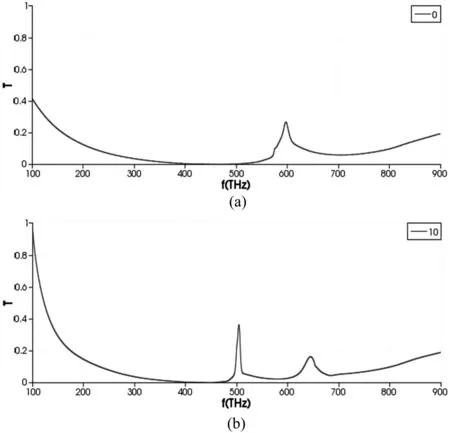
图4　周期500nm,厚度50nm,入射角度不同时光栅的透射光谱。(a)入射角0°,(b)入射角10°

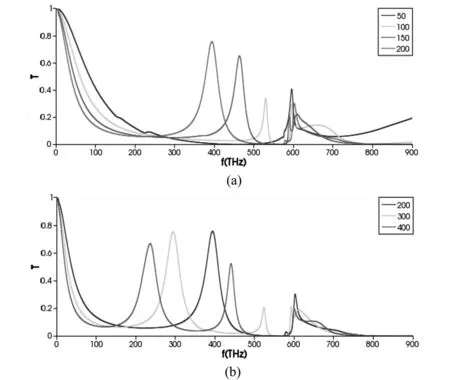
图5 周期500nm，占空比1:9，厚度不同时Ag光栅的透射光谱(a)光栅厚度50nm～200nm，(b)光栅厚度200nm～400nm

4结论

本文讨论了利用FDTD计算亚波长结构色散能带结构的方法，采用偶极子云来作为激发光源，能得到各个方向波矢的电磁特性，有助于准确理解亚波长光栅或者其他结构的超常透射情况。对Ag线栅的计算分析获得了与现有文献一致的结论，表明了该方法的正确性。

[参考文献]

[1]Ebbesen T W，Lezec H J，Ghaemi H F. Extraordinary optical transmission through sub-wavelength hole arrays[J]. Nature，1998(391): 667-669.

[2]Zayats A V, Smolyaninov II, Maradudin A A. Nano optics of surface Plasmon polaritons[J]. Physics Reports, 2005(408): 131-314.

[3]谈春雷，易永祥，汪国平.一维金属光栅的透射光学特性[J].物理学报，2002，51(05):1063-1067.

[4]王亚伟,刘明礼,刘仁杰,雷海娜,田相龙.Fabry-Perot 腔谐振对横电磁波激励下亚波长一维金属光栅的异常透射性的作用[J].物理学报，2011，60:024217 1-5.

[5]J.A. Porto, F. J. Garcia-Vidal, and J. B.Pendry, Phys.Transmission Resonances on Metallic Gratings with Very Narrow Slits[J].Rev.Lett.1999(83):2845-2848.

[6]高本庆.时域有限差分法[M].北京:国防工业出版社,1995:5-21.

[7]王钥，王暄，贺训军.太赫兹波段表面等离子光子学研究进展[C].物理学报，2012.61,137301:1-11.

[8]黄昆.固体物理学[M].北京：高等教育出版社.1998.

[9]S. Collin, F. Pardo,* R. Teissier, and J.-L. Pelouard. Strong discontinuities in the complex photonic band structure of transmission metallic gratings[J]. PHYSICAL REVIEW B, VOLUME 63,033107:1-4.

[10]F.J. Garcia-Vidal, and L. Martin-Moreno. Transmission and focusing of light in one-dimensional periodically nanostructured metals[J]. PHYSICAL REVIEW B, 2002,155412:1-10.

[11]Heinz Raether. Surface Plasmons on Smooth and Rough Surfaces and on Gratings[M]. Berlin, Springer-Verlag, 1988:1-140.

[12]Yanxia Cui, Guohui Li, Kin Hung Fung, Yuying Hao, Sailing He, Nicholas X. Fang. Plasmonic Sensors Based on Rayleigh Anomaly[R].Nov 7-10, Shenzhen, China: Asia Communication and Photonics 2012.

[13]H. Gao, J. M. McMahon, M. H. Lee, J. Henzie, S. K. Gray, G. C. Schatz, and T. W. Odom. Rayleigh anomaly-surface plasmon polariton rexsonances in palladium and gold subwavelength hole arrays[J]. OPTICS EXPRESS,2009,17:2334-2340.

责任编辑：刘海涛

收稿日期：2014-07-18

作者简介：张青，张颖，赵小童，米佳佳，查射曦，安徽师范大学物理与电子信息学院硕士研究生；通信作者：石建平，安徽师范大学物理与电子信息学院教授，博士(安徽 芜湖 241000)。

中图分类号:O472

文献标识码：A

文章编号：1673-1794(2015)02-0050-04