基于分数阶傅里叶变换的聚束SAR成像算法

尹　曼，陈　兵，孟庆华

(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)

基于分数阶傅里叶变换的聚束SAR成像算法

尹曼，陈兵，孟庆华

(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)

摘要针对聚束式合成孔径雷达(SAR)高分辨率成像的问题，在分析聚束SAR回波信号特点和阐述分数阶傅里叶变换(FRFT)原理及性质的基础上，提出了一种基于分数阶傅里叶变换的聚束SAR成像算法，利用分数阶傅里叶变换对线性调频信号良好的能量聚集性，对聚束SAR回波信号进行方位向处理以提高方位聚焦性能，通过理论推导和仿真数据分析了FRFT方位向处理的算法成像性能，并通过实测数据成像，验证了算法的可行性和有效性。

关键词聚束SAR；分数阶傅里叶变换；成像算法

A Spotlight SAR Imaging Method Based on Fractional Fourier Transform

YIN Man，CHEN Bing，MENG Qing-hua

(The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)

AbstractThe paper focuses on high azimuth resolution imaging of a spotlight SAR.An imaging method for spotlight SAR based on fractional Fourier transform (FRFT) is proposed in this paper with the characteristic analysis of the spotlight SAR echo signals and the principles of FRFT.The method improves azimuth focusing performance by using FRFT to process spotlight SAR azimuth signals because of the FRFT’s excellent energy focusing ability to chirp signals.Theoretical derivation and simulation are carried out to analyze the imaging performance of FRFT azimuth processing,and finally the image formed by real data illustrates feasibility and effectiveness of the spotlight SAR imaging method.

Key wordsspotlight SAR;fractional Fourier transform;imaging algorithm

0引言

聚束式合成孔径雷达(Spotlight SAR)是一种高分辨力成像雷达，数据接收时天线波束始终指向同一目标区域，增加了回波的相干积累时间，能获得比条带式SAR更高的方位分辨力，常用于目标精细成像。

由于聚束SAR始终对同一区域成像，其方位向回波信号与条带SAR[1-3]不同，处理方式也不同，常用聚束SAR成像算法有极坐标格式算法(PFA)、距离徙动算法(RMA)[4]和频率变标算法(FSA)[5]等，但PFA和RMA算法都需要插值处理，计算量大，而FSA算法必须在方位向进行尺度变换(Scaling)和去斜(Deramp)处理后才能成像，而且算法都是单纯从时域或频域的角度进行成像处理。本文对聚束SAR方位向回波信号特点进行了详细分析，针对其信号特点提出一种新的聚束SAR成像方法，从时频分析的角度利用线性调频信号在分数阶变换域上良好的能量聚集性和降噪性能，采用分数阶傅里叶变换[6-8](FRFT)对聚束SAR方位向回波信号进行处理，有效提高了图像的信噪比和旁瓣抑制比[6]，使得方位向更好的聚焦，实现了方位向的高分辨率成像。

1算法原理

1.1　分数阶Fourier变换原理及性质

分数阶傅里叶变换是一个线性积分运算[6]，p阶分数阶傅里叶变换的基本定义为：

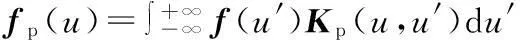
(1)

式中，Kp(u,u′)为分数阶傅里叶变换的核函数。式(1)可以进一步写为：

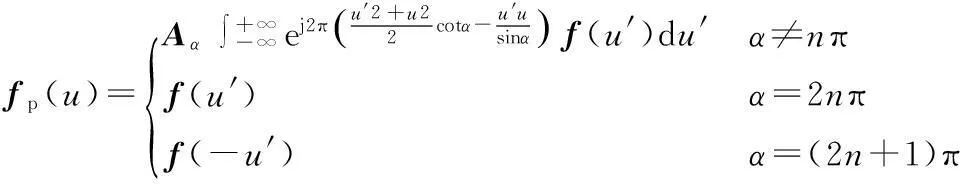
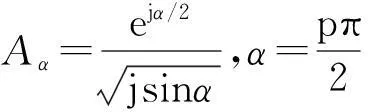
分数阶傅里叶变换可以理解为传统傅里叶变换的推广。若把傅里叶变换看作是将信号从时间轴逆时针旋转π/2到频率轴，即频域，则分数阶傅里叶变换就是将信号从时间轴逆时针旋转任意角度α到u轴，又称为p阶分数阶傅里叶变换。在信号无限长情况下，线性调频信号(LFM信号)在适当的分数阶傅里叶变换域中表现为一个冲激函数，在信号有限长情况下，其幅度表现为极大值，即在某个分数阶傅里叶变换域中，LFM信号具有很好的能量聚集性，因此可以利用分数阶傅里叶变换域对多个LFM信号进行区分。

分数阶傅里叶变换具有线性和旋转可加性等基本性质，是一种很好的时频分析工具，有多种数值计算方法，其中H.M.Ozaktas等[9]提出的分数阶傅里叶变换快速算法运算量为O(Nlog2N)，与FFT的运算量相当，具有实时处理能力。

1.2　聚束SAR方位向回波特点

聚束SAR由于其高分辨力特性，发射信号带宽往往很大，在接收回波信号时常采用去调频处理，以减小信号带宽，降低距离向采样速率的要求。经过去调频处理的聚束SAR点目标回波信号可以表示为[5](基于正侧视模型且以固定距离为参考信号去调频)。

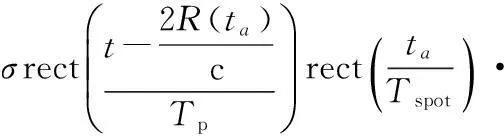
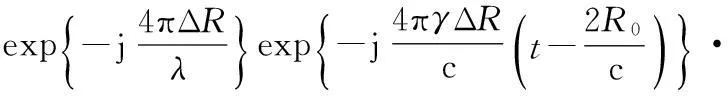
(2)

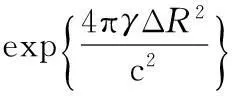
式中，σ为目标散射系数；t和ta分别为距离向时间和方位向时间；Tp为脉冲宽度；γ为调频斜率；λ为发射信号波长；R0为雷达航迹与测绘带中心线的距离；Tspot为合成孔径时间；ta包含在距离差ΔR中。

式(2)第一个相位项反映了回波信号的方位特性，随着ΔR的变化，方位向回波信号将产生多普勒频移。回波信号方位向相位为：

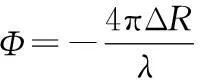
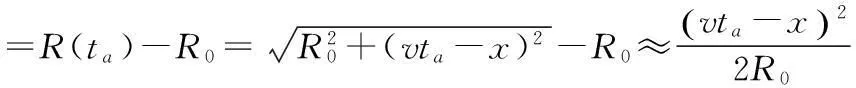
式中,v为平台速度，经过求导处理，方位向多普勒频率为：

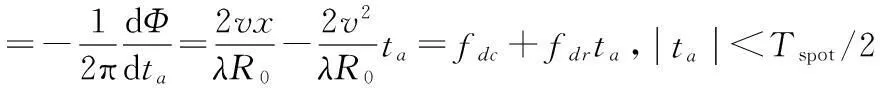
从上面可知，聚束SAR点目标方位向回波近似为线性调频信号，多普勒调频斜率为常数，多普勒质心值是点目标方位向位置x的函数，反映了信号的位置信息。若聚束SAR回波信号未经过去调频处理，通过类似推导，仍可得到相同的结论。

由以上推导可知，位于同一距离，不同方位处的聚束SAR点目标回波是一组时间相同、调频斜率一致的线性调频信号，如图1所示。

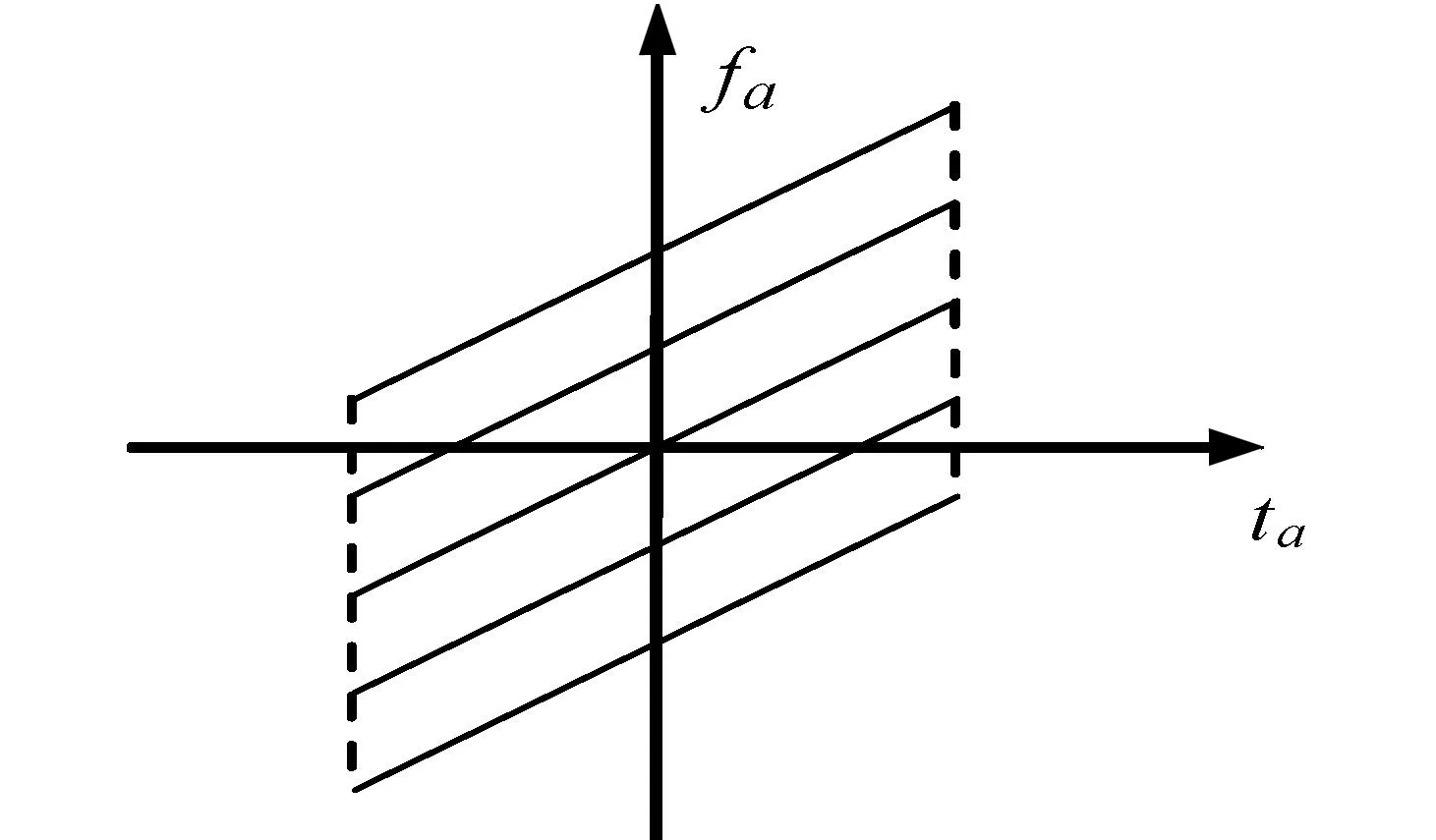
图1　方位向信号多普勒历程

1.3　基于分数阶傅里叶变换的成像算法

合成孔径雷达成像的本质是二维高分辨特性。传统的Deramp处理将聚束SAR方位向回波信号与一个具有相反调频斜率的参考函数相卷[10]，使各方位向信号对应到不同的频率，通过谱分析将各目标点区分。本文从时频分析的角度，利用分数阶傅里叶变换将方位回波信号加以区分，推导如下。

位于x处的聚束SAR点目标方位向回波信号为(忽略幅度影响)：

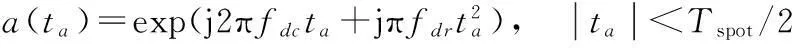
式中，

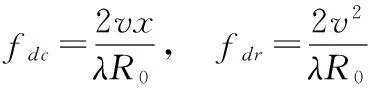
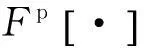
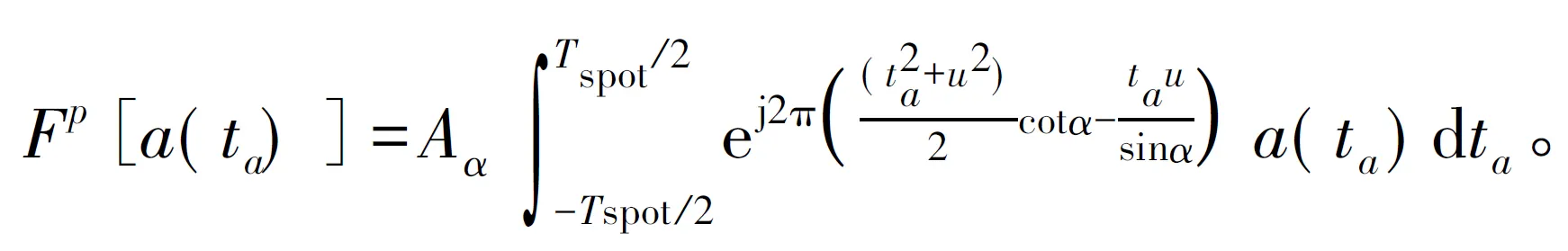
取fdr=-cotα，得到

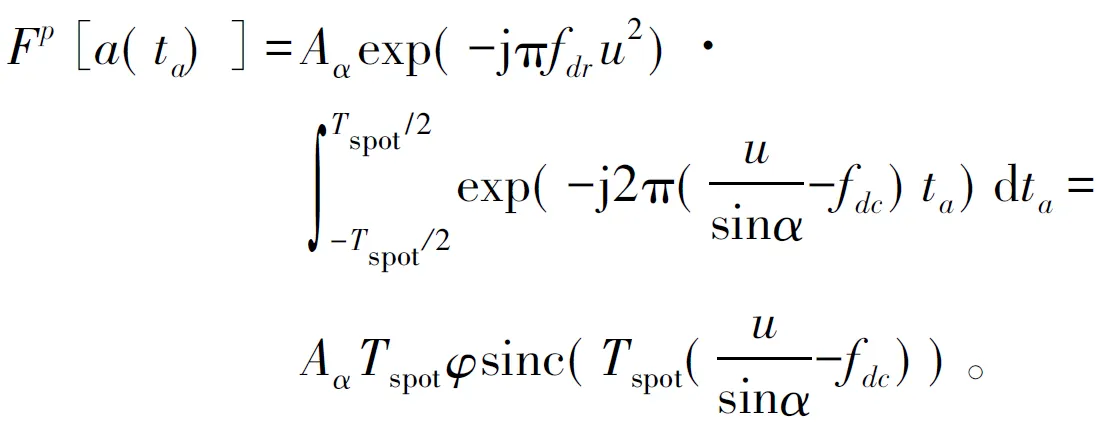
式中，

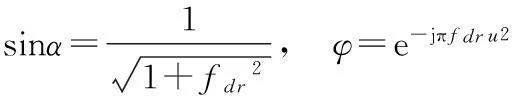
经过分数阶傅里叶变换的信号为辛格函数形式，峰值位置为：

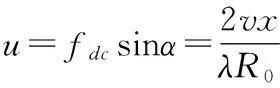
由推导可知，若p=-2arctan(1/fdr)/π，通过p阶分数阶傅里叶变换处理，信号在p阶域表现为辛格函数形式，且峰值位置与点目标方位向位置x有关，不同方位的点目标位于u轴的不同位置，且每个点目标的能量都达到最好聚集，即可以通过分数阶傅里叶变换将各目标点加以区分，达到成像目的。

基于分数阶傅里叶变换的成像算法步骤可归纳为：对于去调频后的原始回波数据，距离向采用频率尺度变换(Frequency Scaling)处理，对于未经过去调频处理的原始回波数据，采用调频尺度变换(Chirp Scaling)处理[4]，消除距离徙动的空变性，然后通过距离徙动校正和二次距离压缩完成距离向聚焦；方位向采用分数阶傅里叶变换达到方位聚焦，最后通过量化处理输出成像结果，整个成像算法流程如图2所示。

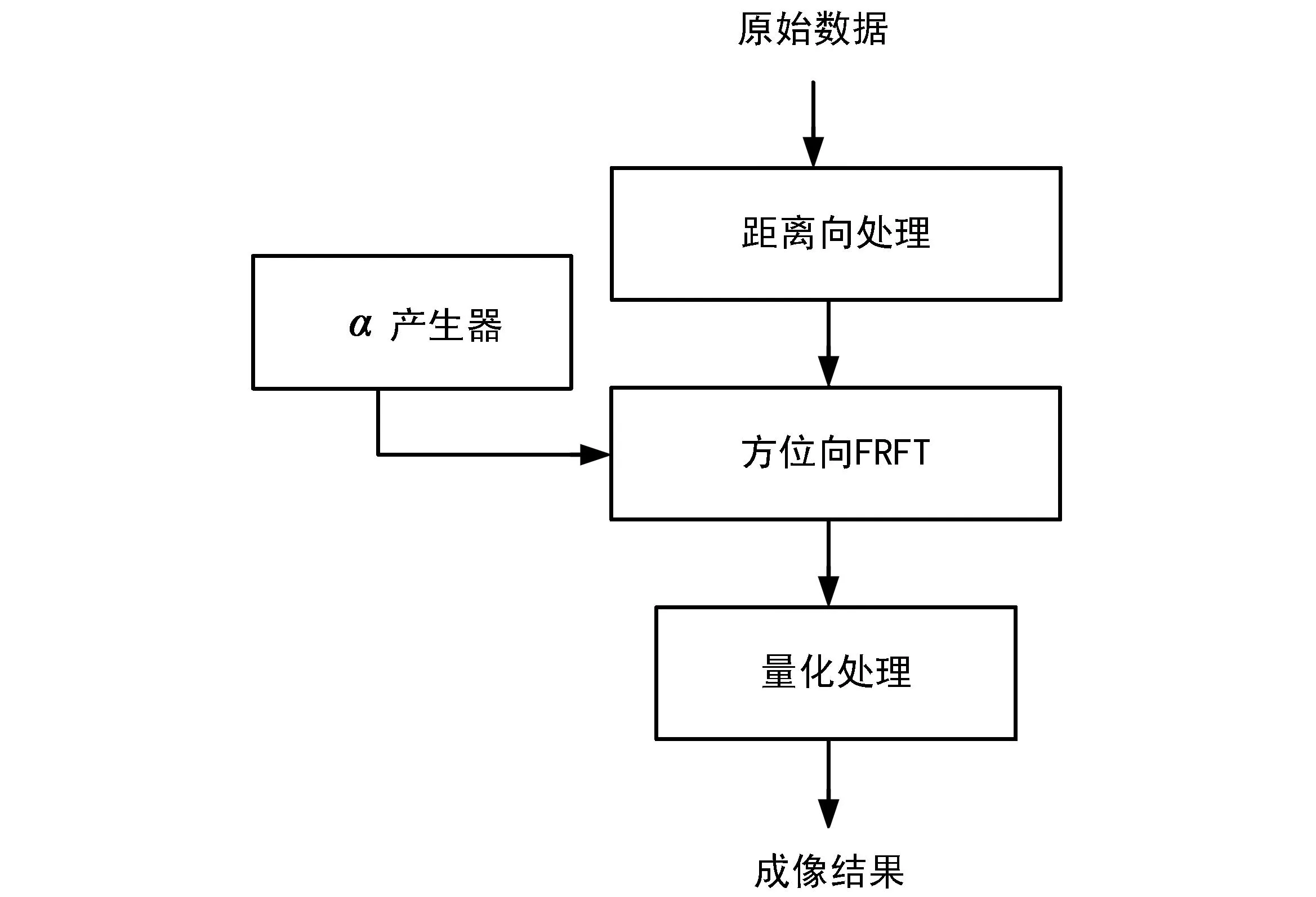
图2　算法流程

2仿真分析

2.1　能量聚集性能分析

考察分数阶傅里叶变换对线性调频信号的能量聚集性能。图3是对同一线性调频信号分别进行Deramp和FRFT处理的结果如图3所示。仿真结果显示，FRFT处理的主瓣更窄，对线性调频信号具有更好的能量聚集性能。

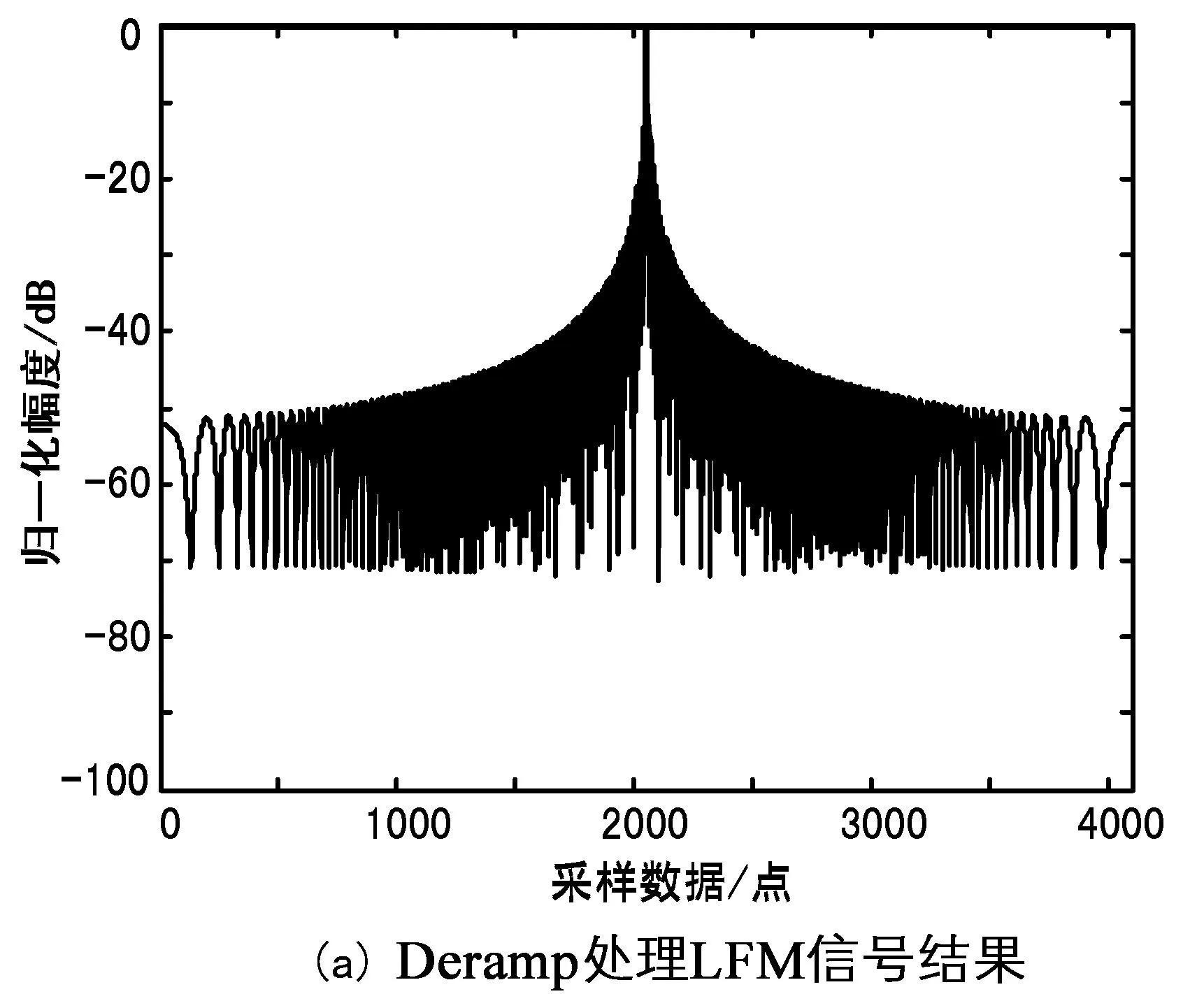
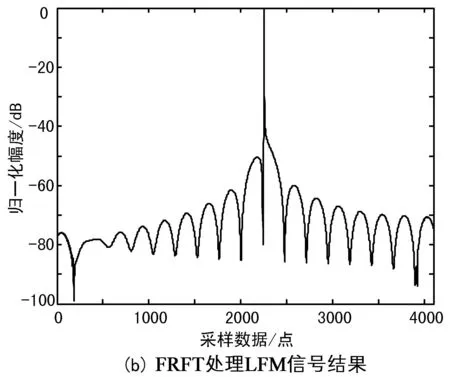
图3　能量聚集性能对比图

2.2　单点仿真数据成像算法验证

仿真参数如下，脉冲宽度：1 μs，信号带宽：133.5 MHz，采样频率：185 MHz，载频：1.22 GHz，脉冲重复频率：250 Hz，合成孔径时间：2.2 s，载机速度：100 m/s。

实验采用的原始数据为去调频后的点目标回波数据，成像处理时距离向采用Frequency Scaling处理，消除距离徙动的空变性并对其进行精确校正，方位向分别采用Deramp和FRFT进行处理，点目标成像效果对比如图4所示。

图4(a)为利用Deramp方式得到的点目标方位向能量分布图，图4(c)为利用FRFT方式得到的点目标方位向能量分布图，利用FRFT方式得到的点目标方位向响应曲线主瓣变窄，能量更加汇聚；图4(b)为利用Deramp方式得到的点目标成像结果图，图4(d)为利用FRFT方式得到的点目标成像结果图，利用FRFT方式得到的点目标成像结果更加汇聚，分辨率明显提高，成像效果更好。

仿真结果表明，利用FRFT进行方位向处理可以成像，而且效果更好。表1的成像性能分析表明，FRFT处理具有更好的峰值旁瓣比和积分旁瓣比。

表1　点目标成像分析

2.3　实测数据成像算法验证

系统参数如下，脉冲宽度：40 μs，带宽：80 MHz，采样频率：100 MHz，波长：0.019 5 m，脉冲重复频率：2 000 Hz，载机速度：118 m/s。

实测数据为去调频后的回波数据，成像处理时距离向仍采用Frequency Scaling处理，方位向采用分数阶Fourier变换处理。实测数据成像结果如图5所示。成像结果显示，利用分数阶Fourier变换可以实现聚束SAR方位向聚焦，验证了算法的有效性。

图5　实测数据成像结果

3结束语

通过对分数阶傅里叶变换和聚束SAR回波信号特点进行讨论，利用分数阶傅里叶变换对线性调频信号的能量聚集性，从时频分析的角度提出了一种基于分数阶傅里叶变换的聚束SAR成像算法，理论分析和仿真试验表明，新算法能够获得更好的峰值旁瓣比和积分旁瓣比，提高了聚束SAR成像的分辨率。

参考文献

[1]张刚,杨立波,祝明波,等.弹载SAR大斜视SPECAN成像算法[J].无线电工程，2012,42(11):10-13.

[2]高跃清,杨晓亮,王磊.调频连续波SAR距离-多普勒成像算法研究[J].无线电工程，2012,42(9):19-22.

[3]张强,梁甸农,董臻.一种弹载条带式SAR成像方法 [J].无线电工程，2006,36(5):39-49.

[4]CARRARA W G.,GOODMAN R S,MAJEWSKI R M.Spotlight Synthetic Aperture Radar Signal Processing Algorithms[M].Boston:Artech House,1995.

[5]MITTERMAYER J,MOREIRA A.Spotlight SAR Data Processing Using the Frequency Scaling Algorithm[J].IEEE Trans.Geoscience and Remote Sensing,1999,37(5):2 198 -2 214.

[6]陶然,齐林,王越.分数阶Fourier变换的原理与应用[M].北京：清华大学出版社，2004.

[7]AMEIN A S,SORAGHAN J J.A New Chirp Scaling Algorithm Bases on the Fractional Fourier Transform[J].IEEE Trans on Signal Processing,Letters,2005,12(10):705-708.

[8]AMEIN A S,SORAGHAN,J J.Azimuth Fractional Transform of the Fractional Chirp Scaling Algorithm.IEEE[J] transactions on geoscience and remote sensing,2006,44(10):2 871-2 879.

[9]OZAKTAS H M,ARIKAN O,KUTAY M A,et al.Digital Computation of the Fractional Fourier Transform.IEEE[J] Trans on Signal Processing,1996,44(9):2 141-2 149.

[10]LANARI R,TESAURO M,SANSOSTI E,et al.Spotlight SAR Data Focusing Based On a Two-Step Processing Approach[J].IEEE Trans on Geoscience Remote Sensing,2001,39(9):1 993-2 004.

尹曼女，(1982—)，工程师。主要研究方向：信号处理及应用。

陈兵男，(1982—)，工程师。主要研究方向：信号处理及应用。

作者简介

基金项目：国家部委基金资助项目。

收稿日期：2015-05-13

中图分类号TN957

文献标识码A

文章编号1003-3106(2015)08-0019-04

doi:10.3969/j.issn.1003-3106.2015.08.06

引用格式：尹曼，陈兵，孟庆华.基于分数阶傅里叶变换的聚束SAR成像算法[J].无线电工程，2015，45(8)：19-22.