基于双重优化的连续手势识别方法

高 畅， 蒋 浩， 毛天露， 王兆其

(1. 中国科学院计算技术研究所移动计算与新型终端北京市重点实验室，北京 100190；2. 四川大学软件学院，四川 成都 610225)

基于双重优化的连续手势识别方法

高 畅1,2， 蒋 浩1， 毛天露1， 王兆其1

(1. 中国科学院计算技术研究所移动计算与新型终端北京市重点实验室，北京 100190；2. 四川大学软件学院，四川 成都 610225)

基于计算机视觉的连续手势识别因为其自然性和便捷性在大型互动娱乐、互动教育等方面得到了广泛应用。在连续手势识别过程中，解决手势分割问题的已有方案多存在计算量大效率低的缺点；解决独立手势识别问题的已有方案多存在训练参数设定过程复杂的缺点。针对这两个问题做出两点优化：其一，提出一种基于隐状态模式归一化的方法对连续手势进行分割，提高了手势分割的效率；其二，提出一种基于参数自反馈调节的独立手势训练和识别方法，降低了独立手势训练的难度，并提高了识别的精度。实验证明，提出的基于双重优化的连续手势识别方法与原有方法相比在精度和效率上都有较大提升。

人机交互；连续手势识别；手势分割；独立手势识别

近年来，人机交互技术快速发展，如何与计算 机进行自然的交互已成为了研究的热点。以往基于键盘和鼠标的交互方式已经十分成熟，出现了越来越多新颖的交互方式[1-3]如语音交互，脑机交互，手势交互，这些新颖的交互方式更加自然、直观，给人们带来了更加良好地交互体验。其中，手势交互技术因为其快捷性和直观性得到了巨大发展，也已经在诸如大型互动娱乐、互动教育等方面得到了成功应用。

手势从运动特点出发，可以分为静态与动态手势。静态手势是仅依靠手的外部形状与轮廓传递信息的方式，被视为动态手势的特例；动态手势是指手的形状与位置都随时间发生变化的手势，可表达更加丰富和准确的信息，也是人们日常生活中最为常用的交流方式之一[4]。其中，用户在三维空间不断挥动手臂，画出图形，计算机得到手的三维空间轨迹数据，从连续数据中自动剔除冗余数据，实时发现并识别出手势种类是一个重要问题，此问题被称作连续手势识别，是本文的研究对象(本文中所涉方法解决无手性变化只考虑手的空间轨迹的问题)。

一般情况下，用户在空间做连续手势时，并不会明确手势的起点和终点，在做不同手势的间隙也存在一些冗余手势。在连续手势识别问题中首先需要识别器剔除冗余数据，明确目标手势的开始和结束位置，被称为手势分割。在手势分割后，识别器对分割好的手势数据进行识别，发出对应指令，这个问题被称为独立手势识别。这两个问题，是连续手势识别过程中存在的主要问题。以往的研究人员已经对这两个问题进行了一些研究，也提出了一些解决策略。

在手势分割过程中，由于数据是实时更新的，所以识别器需要循环对数据流进行检测，不断判断已接收到数据流中是否存在已定义的手势，假如检测到存在已定义的手势，则对手势进行识别并发出指令。以往研究人员主要的思路是为已定义的独立手势和冗余数据分别建立模型，通过把当前数据分别带入这些模型，求出当前数据与这些模型的相似度，通过比较相似度来判断待识别的数据属于冗余数据还是已定义的手势。以往的研究提出了基于隐马尔可夫模型(hidden Markov model，HMM)和阈值模型的手势识别方法[5-8]，这种方案在解决手势分割问题有一定效果，但由于系统实际运行过程中待识别数据往往由冗余手势和已定义手势连接组成，此方法在处理这种情况时往往不能达到良好的效果。

在连续手势被分割之后，需要对分割完成的独立手势进行识别，在独立手势识别过程中，经常会出现训练过程中不能对 HMM参数进行合适的设置，造成识别不准的问题。

针对研究过程中存在的两个问题，本文在原有基础上做出了双重优化：

(1) 针对连续手势识别过程中存在的问题，提出了基于隐状态模式归一化的连续手势识别方法，是指在使用HMM进行手势的训练和连续识别的过程中，均对手势数据进行时序上的逆序处理。经处理后，连续手势中的冗余数据对整体手势的影响都被推后至末端的隐状态，从而在识别过程中隐状态模式归一化为逆序手势连接逆序冗余数据的模式。

(2) 针对独立手势进行识别过程中存在的问题，本文提出了一种基于参数自反馈调节的独立手势训练和识别方法，即在训练过程时，系统会根据样本数据进行自反馈，不断调节训练参数使其达到最佳，自动训练出识别率最高的HMM。

1 相关工作

基于计算机视觉的连续动态手势识别主要分为人手运动轨迹数据收集，手势分割，独立手势识别三个阶段。一般人手运动轨迹数据收集方法主要是通过识别人手特征(手型，肤色)定位手的空间位置和通过识别手持标志物定位手的空间位置两种方法，在以往的研究过程中，通过这两种方法均可以得到人手精确的轨迹数据[1]。本文中假定人手运动轨迹数据收集过程已经完成，重点研究对象在于手势分割和独立手势识别。有关手势分割和手势识别分割，前人主要提出了以下四种方案。

(1) 基于HMM的方法：HMM的基本理论最初提出于20世纪60年代末，它是一个双重随机过程，即状态转移随机过程与观测随机过程。模型的状态不可见，只能通过观察序列观测到，状态转移随机过程决定了隐含状态转移的过程，观测随机过程决定了从隐含状态到观察序列输出间的对应关系。基于HMM曾有人提出了一系列连续手势识别的解决方案[5-8]。在最初的研究过程中，相关研究人员曾试图建立冗余手势的HMM，使用模型就可以判断当前识别的数据是已定义的手势还是冗余手势，但冗余手势种类繁多，此方案虽然可以达到一定效果但整体识别率不佳。Lee和 Kim[8]在此基础上提出了基于HMM和阈值模型的解决方案，通过对比待识别数据在已定义手势对应的HMM和阈值模型的相似度关系来确定当前待识别数据是否是已定义手势。该方案在以往方案的基础上获得了显著提升，但同样存在效率不高，有时还是需要人为进行停顿来分割手势的缺点。

(2) 基于条件随机场的方法：条件随机场(conditional random fields，CRF)是Lafferty于2001年提出的一种判别式概率无向图模型，主要用于标注和切分有序数据。CRF作为一种分类方法，用于动态手势识别时，能很好地描述手势序列间的依赖关系，是进行连续手势识别的一种有效方案。前人在此理论基础上提出了一系列基于 CRF和阈值模型的方法[9-15]，有效地解决了手语识别中的手语分割问题。手语分割与连续手势识别属于同类问题，但基于CRF的方法大多存在训练过程较为复杂，训练比较耗时的缺点。

(3) 基于动态时间规整的方法：动态时间规整(dynamic time warping，DTW)是Sakoe提出的。由于手势在运动速度上存在较大差异，导致手势的采样点不同，DTW 通过在时间轴上调整手势序列以消除这种速度差异。运用该方法调整输入手势的时间轴，使之非线性地映射到模板手势的时间轴上，使得二者之间距离最小，然后再进行模板匹配得到最终识别结果。Alon等[16]提出了基于DTW的连续手势分割和识别框架，在连续手势识别的问题上取得了很大进展。但原始的基于DTW的方法大多存在识别过程比较耗时的缺点。

(4) 基于混合模型的解决方案：在研究过程中，一些学者发现使用混合模型比使用单一模型可以达到更好的效果。如王西颖等[4]提出了一种基于HMM-FNN模型的复杂动态手势识别方法。这种方案整合了HMM对时序数据的建模能力与模糊神经网络的模糊规则的构建与推理能力，将其运用到复杂手势的识别中，取得了良好地识别效果，但使用混合模型同样存在训练过程复杂，识别过程计算量大的缺点。

在大型互动娱乐，互动教育产品应用过程中，多存在多人参与、多人互动的情况，多人参与过程中仍然要求系统具备较高实时性和识别精度。而且为了达到更好的用户体验，系统的训练学习过程应做到简单高效。针对此情况，选用基于HMM和阈值模型的方案，在前人研究基础上做出双重优化，提出了一种高效和高识别精度的识别方法。

2 本文方法

2.1 方法概况

为了达到高效连续手势识别的目的，本文在基于HMM和阈值模型思想的基础上，对训练样本和待识别数据进行隐状态模式归一化处理，显著提高了识别效率。为了在保证识别精度的同时降低模型训练的难度，本文采用了参数自反馈的模型训练方法。图1为本文方法整体流程图。

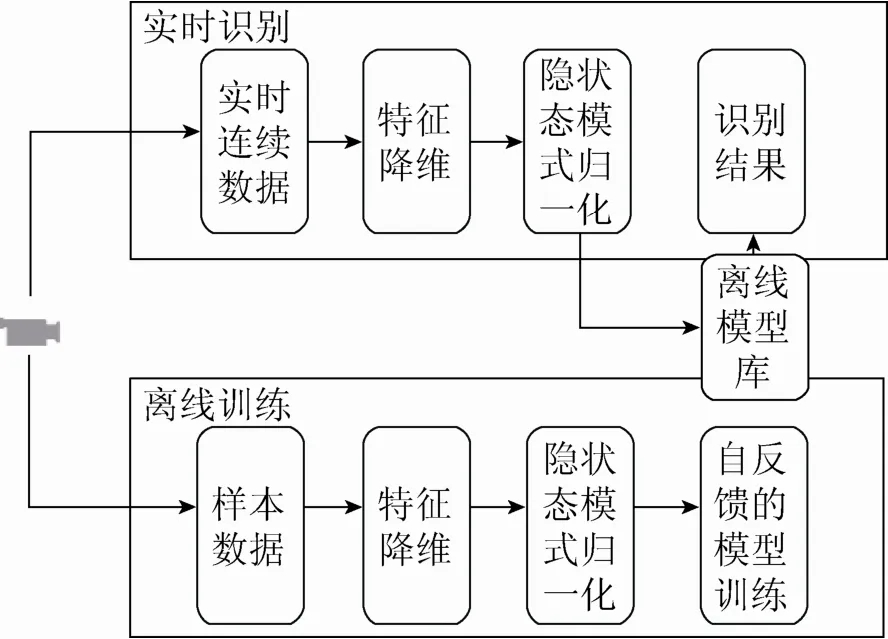
图1 算法框架图

基于隐状态模式归一化的方法主要分为离线训练和在线识别两个模块。这两个模块的理论基础都是HMM。

在离线训练部分中，首先进行的是训练样本收集的过程，然后进行特征提取，最后再使用合适的参数对HMM进行训练，在训练过程中，可采用的是隐状态模式归一化后的HMM。

在实时识别过程中，在收集到实时连续数据之后，要对数据进行相同方法的特征提取，再对隐状态模式归一化处理，最后代入离线模型库得到识别结果，判断此刻的数据是否为已定义的手势。假如识别出已定义手势，则给出识别结果，发出对应指令。

自反馈的模型训练方法是基于一种自动调节并设定训练参数的训练方法，此方法降低了模型训练过程的难度，同时相对于使用先验法人工设定参数的方法，具有更高地识别精度。

2.2 特征降维

当接收到此数据后，首先需要对此数据进行降维处理，将三维空间轨迹投影到可以有效表征手势的二维平面，经处理后原数据降维为（x1, y1）,（x2,y2）,… ,（xt, yt）形式，但此类数据对位置、大小敏感，会对数据的有效识别造成影响，采用经典的求取相邻点间角度正切值的方法，如图2所示，一般选取d种角度(d一般取值为16)原数据可被转换成Ot= (o1),(o2),… ,(ot)(1 ≤on≤d )，经过预处理后的数据排除了手势在空间位置和大小上的影响。

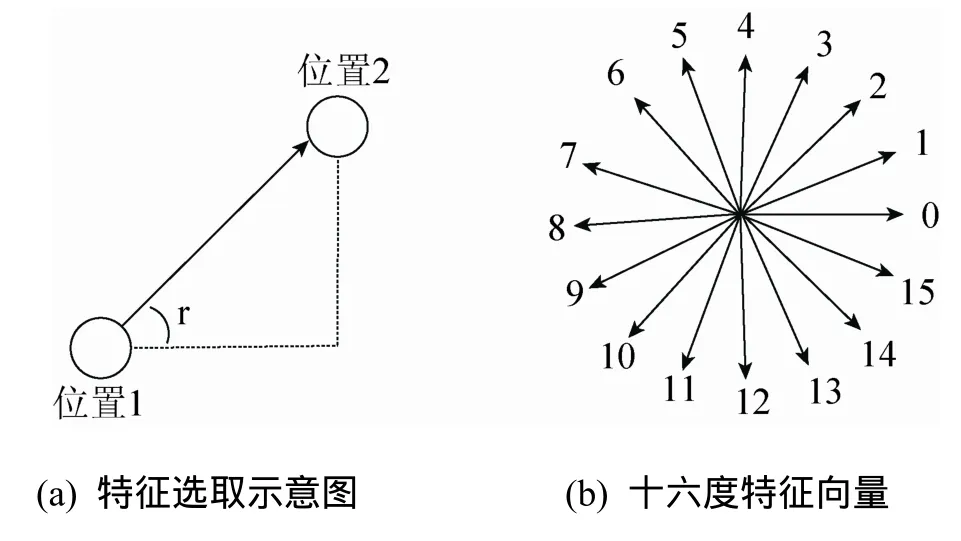
图2 十六度特征向量图

2.3 自反馈的手势训练方法

2.3.1 实际问题描述

想要完成独立手势的识别，就必须先训练出每个手势对应的HMM，在识别过程中，将待识别数据代入各个模型中，然后通过比较此段数据与各个模型的相似度来判断手势类别。想要达到最佳的识别效果，必须正确设置训练时各个参数，在以往的研究中，经常使用人工设置参数的方法进行训练，该方法存在过程复杂且最终结果无法达到最佳的问题，为解决这一问题本文提出了自反馈的手势训练方法。

2.3.2 模型基础

在独立手势识别过程中使用的HMM为左右结构，如图3所示，这种结构的HMM符合手势数据具有时序性的特点。

图3 左右结构的隐马尔可夫模型示意图

本文中假设独立手势有 G种，使用g= 1,2,3,… ,G作为独立手势的序号。第g种手势对应的HMM为λg。

每个λg由 {Ng,Mg,Ag,Bg,πg}组成，其中：

Ng为隐状态集合的隐状态数，在此定义λg中对应的隐状态集合用表示；

Mg为HMM观测值的个数，观测值取值范围用集合 {v1, v2, v3,… ,vd}表示；

A= {ag}(1 ≤i≤ N ,1 ≤j≤N)为N × N的状gij态转移概率分布矩阵，因为本文选用的HMM为左右结构，所以模型的状态转移概率分布应为如下形式。为N × M的观察概率分布矩阵，其中表示t时刻状态为条件下出现观测值 vk的概率。

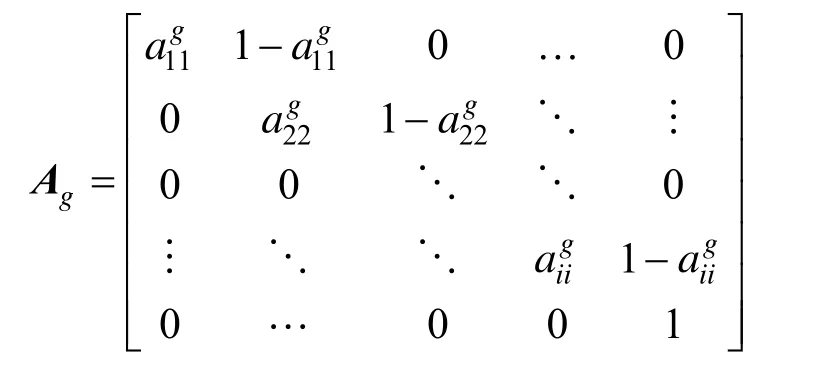
π ={πg,πg,πg,… ,πg}为初始状态分布。

g123N

2.3.3 参数自反馈调节过程

当假设第g种手势的训练样本有 Sg个，那么表示第 g种手势的第 s个样本的轨迹序列(1,2,3,… ,Sg)，则手势g对应的训练样本集合可以使用表示。

若使用Baum-Welch算法对训练数据Tg进行训练，最终得到第g种手势对应的HMM为λg。前边已经提到λg由{Ng,Mg,Ag,Bg,πg}五个组件构成。在训练之前，需要对这5个组件赋初值，即：

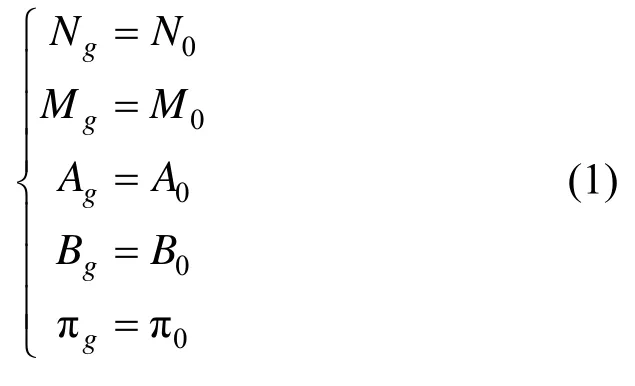
训练结果λg会与初始值和Tg有一定的函数对应关系，在此使用：

表示这种对应关系，这个问题对应的是HMM中的参数学习问题，其经典解法是Baum-Welch算法，需要特别注意的是，λg中的组件 N, M ,π在初始化后不会因训练过程而发生改变。

初始参数设定完毕后进行训练即可得到其对应HMM λg。将一个训练样本重新带入模型λg可以求得此训练样本对于此模型相似度δ(,λ)s ggt ，这个概率的求解过程对应HMM中的解码问题，这个问题是指在给定模型参数λ和观测序列O时，寻找最有可能产生观测序列 O的最佳隐状态序列的过程，此处的概率是指对应的最佳隐状态序列产生观测序列的概率，此概率通常使用Viterbi算法求解，使用此概率表征一个训练样本与模型的相似度，并使用样本集所有样本对应概率的平均值表征此模型的整体相似度。在此定义为：

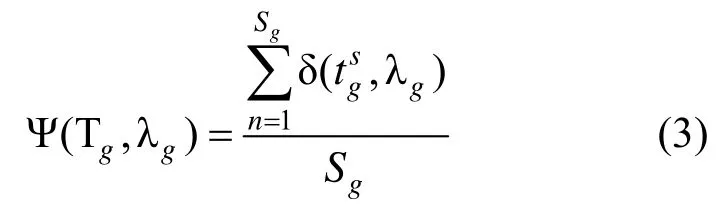
为使用训练样本Tg训练出的模型与训练样本的相似度。

将式(2)带入式(3)可以得到式(4)：

这个问题可以归纳为一个优化问题，在初始化时，如下参数(初始参数均根据先验知识得出)可以使取值达到最佳效果：其中，GESTURE LENGTH为Tg中所有元素长度的平均值；

d为特征值的种类数，d=16

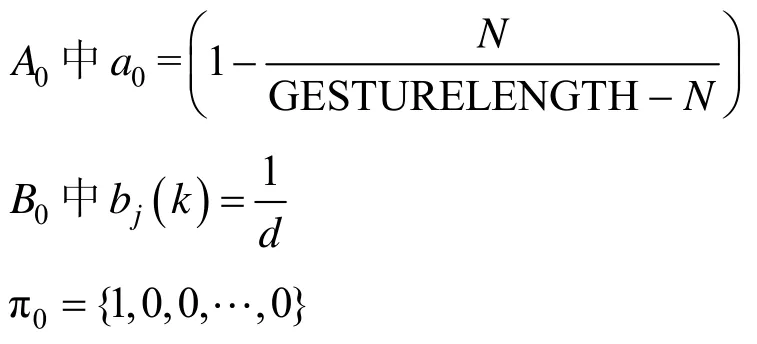
此问题可以使用随机优化算法求得近似最优解，在下降过程中，保持M和π的值不变，通过自反馈调节改变A和B，N的值使问题达到满足的最优解。

2.4 隐状态模式归一化连续手势训练/识别方法

2.4.1 实际问题描述

图4中所绘制的问题为连续手势识别过程中存在的核心问题，即在包含冗余数据流中分割出已定义手势并对其进行识别。

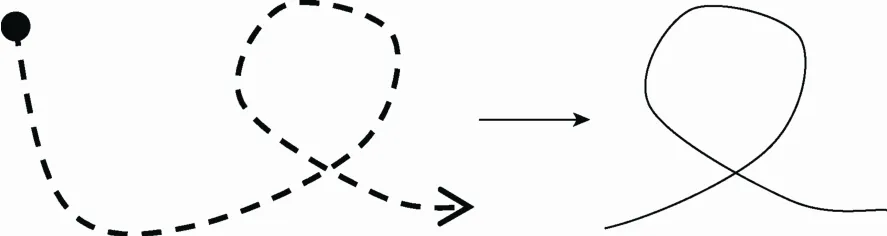
图4 连续手势识别示意图

因为连续手势的绘制和识别过程均具有实时更新性，且当用户完成一个手势的绘制时，用户所绘制手势一定处于数据流末尾，所以连续手势识别问题可以转换为前端带有冗余手势的独立手势识别问题。

2.4.2 数学问题转化

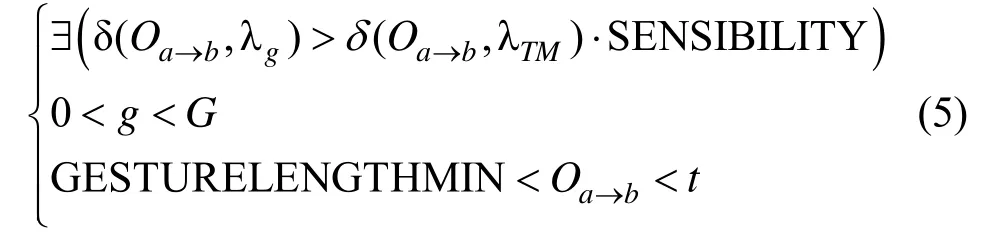
2.4.3 问题解决方法

本文中使用Viterbi算法求解δ(Oa→b,λg)的值。Viterbi算法解决的是解码问题，即在给定模型参数和观测序列，寻找最有可能产生此观察序列的隐状态序列的过程。使用 Viterbi算法求解出δ(Oa→b,λg)，还会得到与此对应的隐状态序列

因为手势序列具有时序性且本文中采用的是左右结构的HMM。所以当 Oa→b为一个独立手势时(如图 5(a)所示)，此种情况下 qT*具有一定的均匀性，这种情况下δ(Oa→b,λg)处于正常前端的冗余手势会对隐状态进行匹配，从而打乱后端独立手势与相应隐状态的正确匹配，这种情况下 s( Oa→b_λg)会非常低，无法满足式(5)。而在连续手势数据中，经常会出现如图5(b)或者更为复杂的连有冗余手势的独立手势，由此可见，使用滑动窗口进行多次匹配才能切分出正确的独立手势并完成识别，此类方案的实现方法及分析如下。

图5 隐状态序列与轨迹序列关系图

方法1(原始方案). 通过滑动窗口暴力求解的方法

训练过程：

在训练过程中，使用自反馈的手势训练方法构造每个手势对应的λg，再使用相应阈值模型的构造方法构造阈值模型λTM。

识别过程：

连续手势识别的过程是实时的，所以理论上需要在每次数据更新时进行识别。又因为识别过程是实时检测的，所以连续手势数据有以下特性：

特性1：当用户完成一个手势的绘制时，用户所绘制手势一定处于数据流末尾。即在连续手势数据流Ot= (o1),(o2),… ,(ot)中满足式(5)的理想Oa→b一定满足b = t。

根据特性1，只需在数据更新时检测所有可能的 Oa→t并计算其是否满足式(5)即可，a可能的取值范 围 为 [t-GESTURE LENGTH MIN，t-GESTURE LENGTH MAX ](此处出现的GESTURE LENGTH MAX代表在样本集中最长的样本平均长度)。因为在实际情况中 Oa→t，Oa+1→t,…,Oa+step→t这些相邻数据差异性较小，所以对这些相邻类似数据进行一次检测即可，这种情况下算法运行的总时间：

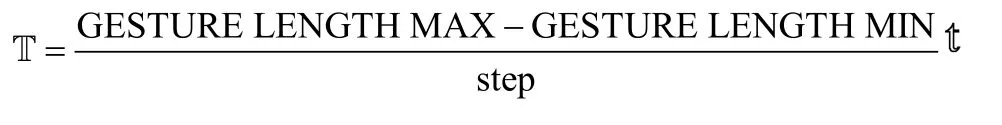
实验中发现一般情况下想要达到良好的识别效果一般 T ≥10，此种方法的计算量较大。

方法2. 隐状态模式归一化连续手势训练/识别方法

针对此情况，所提出的使用隐状态归一化的训练/识别方法，可以显著提高识别的效率，减小计算代价。

训练过程：

在训练过程中，在带入每个手势所对应的HMM λg进行训练之前，先要对数据进行时序上的逆序处理，即使用Tg构造其逆序向量使的逆序，再将 Qg分别带入每个λg中求得 AgBg的值。在每个手势对应的λg训练完成后，再使用相应阈值模型的构造方法构造阈值模型λTM。

识别过程：

在隐状态模式归一化的识别过程中，需先对数据进行时序上的逆序处理，即使用 Ot构造其逆序向量Rt，使 Rt=(ot),(ot-1),… ,(o1) =(r1),(r2),… ,(rt)。在 Rt中寻找子序列 Ra→b使子序列满足式(5) (其中Oa→b替换为 Ra→b)，由特性1可知，当用户完成一个手势时，所绘制手势一定处于数据流末尾，因此处连续手势数据进行了逆序处理，所以即在连续手势数据流 Rt中满足式(5)的理想 Ra→b一定满足a=1;在本方法的检测过程中恒定设定 b为GESTURE LENGTH MAX。

用户绘制的待识别的手势有以下几种情况。①手势为已定义手势中的最长手势，此时 R1→b是此手势的逆序，必然满足式(5)即可识别出此手势。②当手势为短手势时， R1→b为此手势的逆序连接一小段冗余数据的逆序。在此情况下将 R1→b带入各个HMM使用Viterbi算法计算 s( R1→b_λg)时，会匹配到其对应正确的隐状态序列，而冗余数据的影响会集中到最后的隐状态上，从而使冗余数据对整体的影响降到最低。这种情况下每次数据更新只需进行一次检测，算法运行的总时间：

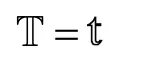
由此可见，改进后的方法比原方法效率提高10倍以上。

3 实验与算法性能比较

为了验证本文中所提出的算法的预测精度及在实际连续手势识别中对冗余手势处理的性能，本节将在实际手势数据集上对算法进行测试和性能比较试验。

3.1 实验数据源及实验环境

本文共邀10位用户(年龄20～30岁，男、女各5位)参与连续手势的训练和识别过程，其识别对象为图6中四种手势。训练数据由用户使用鼠标在2D空间进行绘制，每种手势收集 40组样本数据进行训练。在识别测试过程中，用户在3D空间挥动手掌，计算机得到实时的轨迹数据进行识别。本实验用计算机处理器为 AMD Athlon(tm) || P320 Dual-Core CPU，内存4.0 GB，操作系统为Windows 8。

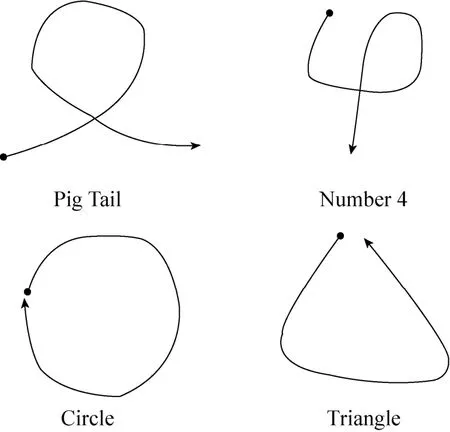
图6 手势种类图

3.2 自反馈的训练方法相关实验

实验证明，训练HMM时所选取的参数N和A，会对模型的相似度Ψ(Tg,λg)造成影响。

表1为隐状态数N对模型精度影响表(识别手势为Number 4，HMM中的其他几个参数设置相同)。

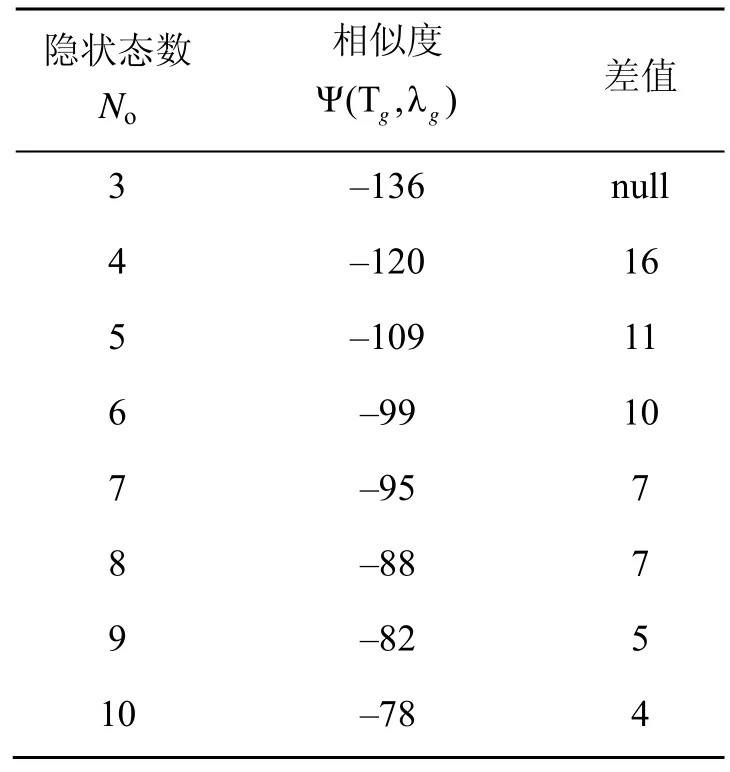
表1 隐状态数N对模型精度影响表

由表1可知，当隐状态数目增多时，模型的相似度会相应升高，但识别时间也会相应增加使用自反馈的参数调节方法，系统会选择7作为此手势的隐状态数，这种选择为满足的具有最高识别精度的解。

图7为对训练参数A对模型相似度影响表。(识别手势为Number 4，HMM中的其他几个参数设置相同)。

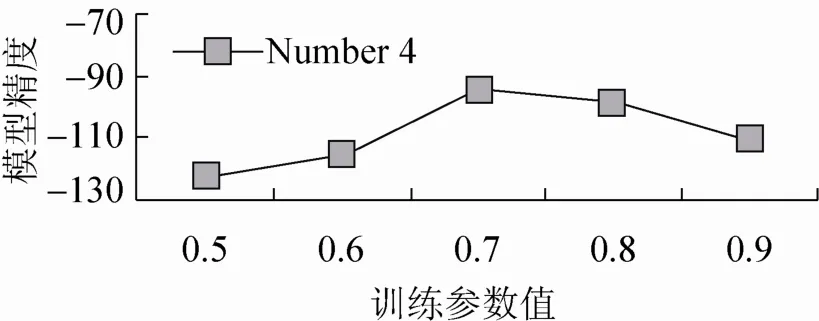
图7 训练参数A对模型相似度影响图

通过以上两实验可以得知，训练时初始化参数中的N和A会对模型精度有较大影响，通过自反馈的训练方法，可以找到满足 〈max使模型精度Ψ(Tg,λg)为最大的训练参数值。

使用自反馈的模型训练方法，最终找到的模型训练参数如表2中所示。

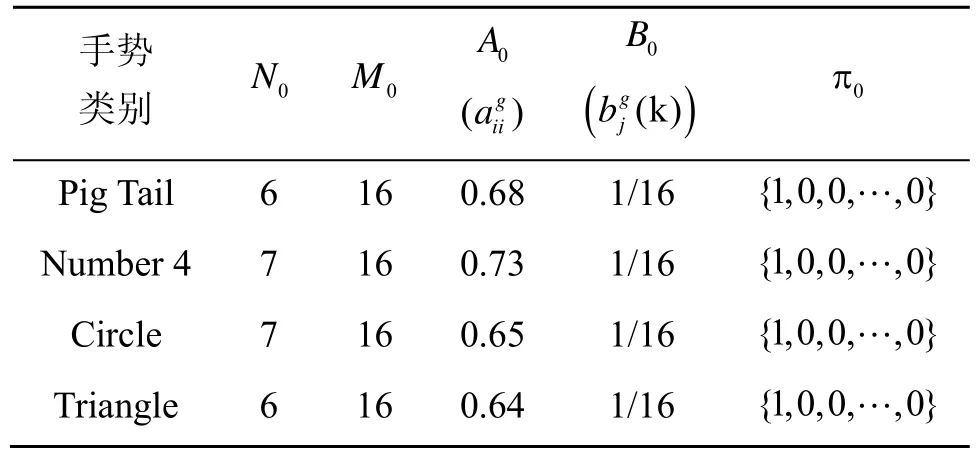
表2 模型训练参数表

为了证明本文中自反馈调节设定参数的方法比以往使用先验法设定参数的方法具有提高识别精度的效果。在此进行了对比实验，首先，统计了使用自反馈调节的方法进行训练的模型识别率，然后统计了直接使用先验法设定参数训练的模型识别率。本文方法与原有方法识别率对比如表3所示。

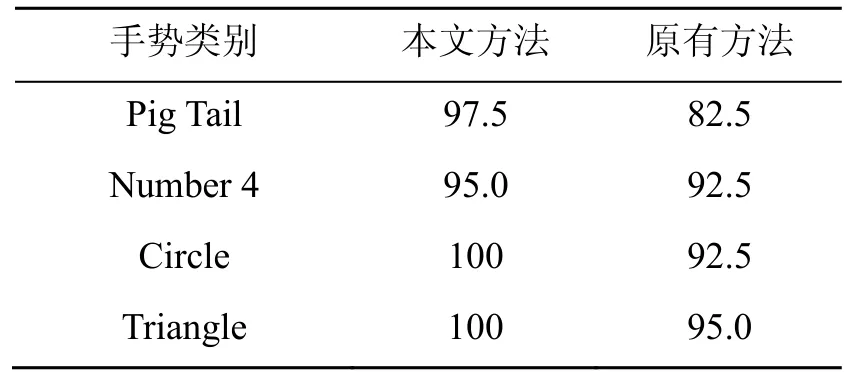
表3 识别率对比表(%)

由表3可见，通过本文自反馈调节方法训练得出的模型识别率比原方法在识别率上有所提升。

3.3 隐状态模式归一化的训练/识别方法相关实验

2.4 节讨论发现使用隐状态模式归一化的训练/识别方法可以比原方法的速度快 10倍左右。设置对比试验为检验此结论的正确性，收集每种手势40组含有冗余数据和已定义手势的连续数据。分别计算两种方法每次数据更新需要的算法执行时间T。

图8为使用原始方法的算法执行时间图，图9为使用隐状态模式归一化的训练/识别方法的算法执行时间图。此两图中横轴为手势类别，纵轴为算法运行时间，图中最大值指在一次实验中所有测试结果(算法运行执行时间)中的最大值，最小值指在一次实验中所有执行时间测试结果(算法运行执行时间)中的最小值，平均值即为所有结果的平均值。

由图8数据可知，使用原始方法的算法的执行时间基本在500～600 ms之间；由图9可知，使用隐状态模式归一化的训练/识别方法的算法执行时间基本在40～60 ms之间，由于硬件和系统实际运行环境的不同，实际测量中的函数测量时间可能不同，但整体上使用隐状态模式归一化的训练/识别方法的算法运行时间为原始方法算法的执行时间的十分之一左右，由此可见系统执行效率得到了较大提升。

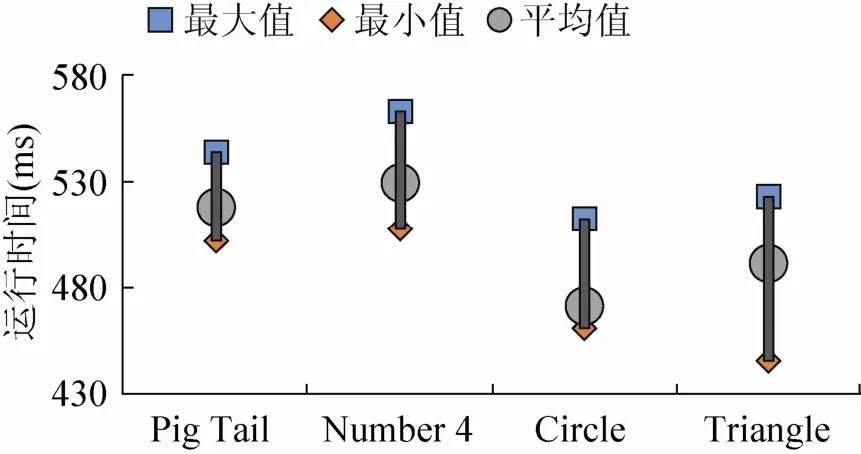
图8 使用原始方法的算法执行时间图

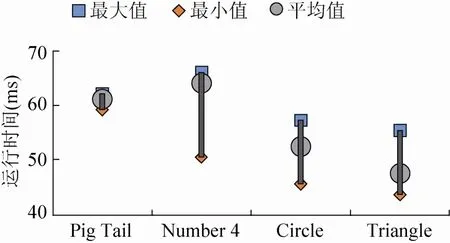
图9 使用隐状态模式归一化的训练/识别方法的算法执行时间图

4 结 束 语

本文主要有两点贡献，其一，提出了一种基于隐状态模式归一化的方法对手势进行分割，提高了手势分割的效率和精确度；其二，提出了一种基于参数自反馈调节的独立手势训练和识别方法，降低了独立手势训练的难度，并提高了识别的精度。实验证明，本文提出的基于双重优化的连续手势识别方法与原有方法相比在精度和效率上都有较大提升。

由于HMM中参数众多，选择不同的状态值，可使整个模型架构发生变化，所有相关参数均需重新计算，因此，自反馈参数调节过程可能需要一定时间，本文虽为调节时间设置了一个上限值，但在此上限值内的寻优很有可能陷入局部最优而不是全局最优解的情况，此问题的解决还需要在以后的研究过程中再继续进行探讨。

由于在实际情况下可能会出现多个人同时做出手势的情况，本文下一步将对多人连续手势识别进行研究。

[1]LaViola Jr J J. 3D gestural interaction： the state of the field [J/OL]. ISRN Artificial Intelligence, 2013-[2014-06-11]. http：//dx.doi.org/10.1155/2013/514641.

[2]Mistry P, Maes P. SixthSense： a wearable gestural interface [C]//ACM SIGGRAPH ASIA 2009 Sketches, 2009：11.

[3]Dipietro L, Sabatini A M, Dario P. A survey of glove-based systems and their applications [J]. Systems, Man, and Cybernetics, Part C： Applications and Reviews, IEEE Transactions on, 2008, 38(4)： 461-482.

[4]王西颖, 戴国忠, 张习文, 等. 基于 HMM-FNN 模型的复杂动态手势识别[J]. 软件学报, 2008, 19(9)：2302-2312.

[5]Pang Haibo, Ding Youdong. Dynamic hand gesture recognition using kinematic features based on hidden markov model [C]//Proceedings of the 2nd International Conference on Green Communications and Networks 2012 (GCN 2012), 2013： 255-262.

[6]Wan Jun, Ruan Qiuqi, An Gaoyun, et al. Gesture recognition based on hidden markov model from sparse representative observations [C]//Signal Processing (ICSP), 2012 IEEE 11th International Conference on, 2012： 1180-1183.

[7]Bilal S, Akmeliawati R, Shafie A A, et al. Hidden Markov model for human to computer interaction： a study on human hand gesture recognition [J]. Artificial Intelligence Review, 2013, 40： 495-516.

[8]Lee H K, Kim J H. An HMM-based threshold model approach for gesture recognition [J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1999, 21(10)： 961-973.

[9]Chung H, Yang H D. Conditional random field-based gesture recognition with depth information [J]. Optical Engineering, 2013, 52(1)： 017201.

[10]de Souza C R, Pizzolato E B, dos Santos Anjo M. Fingerspelling recognition with support vector machines and hidden conditional random fields [C]//Advances in Artificial Intelligence-IBERAMIA 2012, ed： Springer, 2012： 561-570.

[11]Liu Techeng, Wang K C, Tsai A, et al. Hand posture recognition using hidden conditional random fields [C]// Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM '09), 2009：1828-1833.

[12]Wang S B, Quattoni A, Morency L, et al. Hidden conditional random fields for gesture recognition [C]// Computer Vision and Pattern Recognition, 2006 IEEE Computer Society Conference on, 2006： 1521-1527.

[13]Liu Fawng, Jia Yunde. Human action recognition using manifold learning and hidden conditional random fields [C]// Young Computer Scientists, 2008. ICYCS 2008. The 9th International Conference for, 2008： 693-698.

[14]Song Yale, Demirdjian D, Davis R. Multi-signal gesture recognition using temporal smoothing hidden conditional random fields [C]//Automatic Face & Gesture Recognition and Workshops (FG 2011), 2011 IEEE International Conference on, 2011： 388-393.

[15]Yang H D, Sclaroff S, Lee S W. Sign language spotting with a threshold model based on conditional random fields [J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2009, 31(7)： 1264-1277.

[16]Alon J, Athitsos V, Yuan Quan, et al. A unified framework for gesture recognition and spatiotemporal gesture segmentation [J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2009, 31(9)：1685-1699.

A Double-Optimization Approach for Continuous Gesture Recognition

Gao Chang1,2, Jiang Hao1, Mao Tianlu1, Wang Zhaoqi1
(1. Beijing Key Laboratory of Mobile Computing and Pervasive Device, Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100190, China; 2. College of Software Engineering, Sichuan University, Chengdu Sichuan 610225, China)

The continuous gesture recognition based on computer vision has been successfully applied in the field of large interactive entertainment and large interactive education. During the process of continuous gesture recognition, the first key problem is gesture segmentation, the existing solutions of this problem mostly have the disadvantage of low efficiency; the second problem is independent gesture recognition, the existing solutions of this problem mostly have the disadvantage of complicated training problem. A double-optimization approach for these problems is proposed. Firstly, in order to improve the efficiency of hand gesture segmentation, a hidden state mode normalization method is given for continuous gesture segmentation. Secondly, to reduce the complexity of independent gesture training and improve recognition accuracy, a training method is presented based on parameter self-feedback regulation for independent gesture recognition. Experiments have shown that our methods greatly enhance accuracy and efficiency.

human computer interaction; continuous gesture recognition; gesture spotting; single gesture recognition

TP 181

A

2095-302X(2015)01-0102-09

2014-08-11；定稿日期：2014-08-20

国家“863”高技术研究发展计划基金资助项目(2013AA013902)

高 畅(1993-)，男，河北保定人，本科。主要研究方向为人机交互、模式识别。E-mail：gaochang@ict.ac.cn

蒋 浩(1982-)，男，湖南株洲人，助理研究员，博士。主要研究方向为虚拟现实、智能人机交互。E-mail：jianghao@ict.ac.cn