温度变化对振动信号传输的影响简述

马建瑞

（重庆机场集团有限公司，重庆401120）

随着经济的迅速发展，对各种仪表设备的性能提出了更高的要求。为了提高和改善仪表设备的性能，需对仪表设备进行测试。仪表设备运行时，其内部的损耗大部分以热量的形式转换，使温度变化对仪表设备振动信号的传输产生极大的影响，故在仪表设备工程中，对信号传送设备也提出了更高的要求。因此，了解不同温度环境下振动信号的传输情况来指导仪表设备的运作具有重要意义。

1 振动信号传输的模型建立

由于传输导线具有对称性，取四分之一的导线模型进行研究分析，如图1所示，振动信号通过导体导线进行传送，而外界环境的对流只作用于导体的表面。

整个热量传递的过程是导体向环境吸收热量同时不断地向环境释放热量的循环过程，且该过程具有一定的热电耦特性。

图1中：k为导体的导热系数；h为对流给热系数；r1和r0分别为导体的外、内半径；Ta为导体周围环境温度；R和I分别是导体的电阻和通过导体内部的电流。

基于热传导基本方程及麦克斯韦方程，电场中的静电分布可表示为：

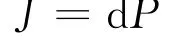
式中，ρ表示材料的电阻率；E表示所处电场的电场强度；J表示通过导体的电流密度；P表示电势向量。

图1 传输线模型

假设传输线材料具有均匀分布性，且导体外部绝缘层与周围环境形成稳定对流，热量在绝缘层与导体内部之间以热传导的方式传递，那么，热量传递方程可表示为：

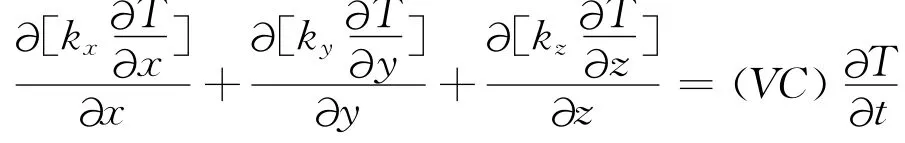
式中，C为导体材料的比热；V为材料密度；k为材料导热系数；T表示导体本身的温度，并且V、C、k都随温度的变化而改变。当导体中有电流通过时，便会产生焦耳热（qjoule），则建立热电耦合有限元矩阵方程有：

式中，T表示温度矩阵；V为电势矩阵；CV为介电常数矩阵；CT为比热系数矩阵；KT为热传导矩阵；KV为点传导矩阵；I为输入导体的电流；Q为导体热量。

在只考虑外部对流的情况下，可得出热平衡方程

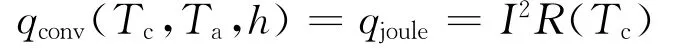
式中，qconv为对流传热量；Tc、Ta分别为环境温度和导体温度。从热平衡关系中可看出焦耳热与输入电流密度有直接的关系，所以输入电信号大小的变化必然会引起热量传递的变化，从而导致传送导体温度的变化［1］。

2 信号传送过程的模仿计算与结果分析

若采用有限元分析软件建立图1所示的导线模型，模型的网格划分用3D热电传导单元，其中r0＝0.175 mm，r1＝1.8 mm，在20℃下，k与C的取值分别为3 95.35 W／（m·℃）、380.58 J／（g·℃）。

在常温下，信号通过传输线传送时是基本保持不变的，本文主要对不同温度下信号传送变化进行分析。在一定频率范围内，存在I0＝Imax／，其中，I0为电流有效值，Imax为输入信号的最大值［2］。

2.1 常温下的信号传送过程

假设振动测试信号经转化后通过导体的有效电流值I0为1 A，环境温度为20℃，根据输入信号与输出信号的变化曲线，可得出输出信号有所降低，即导体内部温度提升到高于导体表面温度分布，随着时间的积累最终导致输入与输出信号发生变化。

当环境保持恒温20℃时，输入信号与输出信号基本相同。根据电流密度与材料的电阻率可计算出通过截面的电压。初始时，通过导体的截面电压为9.6989 mV，一段时间之后降为9.594 mV，对应导体温度21.6℃，其输出误差为1%；当输入信号在20 mA～1 A时，输出电流信号和输入电流信号基本不变，输出电压的最大值也保持恒定。测试过程中，如果环境温度保持恒定，信号有效幅值不高于某一定值，则信号基本可以稳定传输，即当测试信号一定时，功放的选择有利于提高信号的唯一准确性［3］。

2.2 对流给热系数对信号输出的影响

在对流条件下，由自然对流准则可得传输线表面对流给热系数h＝16.3 W／（m2·℃）。由于h受到多种外部条件的影响，同时实际环境的变化特性，为确保传输信号的稳定，将换热系数设置为5～100 W／（m2·℃），包括导线与空气间受迫对流与自然对流的影响，当对流给热系数达250 W／（m2·℃）时，则换热系数为蒸汽通过导线时的对流换热系数。

假设环境温度100℃，输入电流恒定。那么对流系数的增加导致导体与环境的换热量也增加。导体内部温度随对流系数的减小而减慢，达到一定温度所需的时间增长，最终导体温度维持在100℃左右。

假设输入电流信号为1 A，外界温度为10℃，导线与环境间存在对流换热，则可得到不同对流系数下输出信号的变化规律为：温度升高的时间随着对流系数的不同而不同；对流系数分段式的影响电流输出信号；电信号的输出及灵敏度随着温度的改变而改变［4］。

2.3 输入信号的变化对信号输出的影响

传输导体的发热量主要取决于输入电信号高低的影响，过大的电信号则会导致过高的温升。本文主要分析不同电流幅值下的信号输出。若定义输入信号与输出信号的偏差表示电流信号的偏差，即WC＝（Io－Ii）／Ii，其中，WC为偏差系数，Io、Ii分别表示输出信号和输入信号，由此式可得到偏差曲线。随着导体温度的升高，偏差逐渐增大；当电信号在20 mA～1 A时，偏差曲线大致相同，而当电信号高于1 A时，偏差逐渐增大，由于受到热传导的影响，当导体温度高于100℃时，绝缘层开始失去屏蔽作用。

参照各自的无对流状态，进行对截面的电压幅值分析，若用WV表示误差系数，存在关系WV＝（U0－Ut）／Uo，其中Uo、Ut分别表示无对流时的截面电压幅值和对流作用下不同输入信号的电压幅值。则可得到误差变化曲线如图2所示（以电流幅值为50 mA、500 mA和5 A为例）。

从变化曲线中可看出：当输入电流为50 mA、500 mA时，起初误差不稳定，但随着时间的增加逐趋稳定；当输入电流为5 A时，电压幅值变化极不稳定且波动极大。通过分析无对流条件下，导体温度的升高随着输入电流的增大而增大，且电流越大增大速率越快。当有对流作用存在时，虽然温升的速度降低了，但不能完全阻止升温，因此，信号的传送仍不稳定［5］。

3 结 论

环境温度的变化对振动信号传输的影响较为复杂，本文采用有限元法建立模型，通过计算分析得出如下结论：

（1）传输导线与环境间的对流传热及导体内部热源的存在，导线的温度升高，使导体的材料属性变化，影响信号传输的精确性。

（2）传输导线表面的对流系数受外界温度等因素的影响，对流系数不同，作用时间不同，其对信号的影响程度也不同，维持对流系数的稳定有利于信号的稳定传送。

（3）输入电流不同产生的温升不同，对信号输出的影响也不同。随着输入信号的增大输出信号的偏差越大，过高的输入电流可能会损坏传输线，影响测量的准确性［6］。

［1］ 门秀花，李舜酩，杨 东.温变环境中测试信号传输的仿真及试验［J］.航空动力学报，2011，3（07）：110-111.

［2］ 左泽敏，李舜酩，郑娟丽.相关分析在机械振动信号处理中的应用［J］.机械制造与自动化，2009，6（01）：122-123.

［3］ 李舜酩，雷衍斌.基于负熵的转子混叠振动信号盲识别［J］.中国机械工程，2009，9（04）：133-134.

［4］ 李永建，李舜酩，郝青青，沈 峘.微弱振动信号自适应采集系统设计［J］.现代电子技术，2009，4（05）：156-157.

［5］ 辛江慧，李舜酩，沈 峘.一种新的智能避障转向控制方法［J］.传感器与微系统，2009，7（03）：93-94.

［6］ 门秀花，李舜酩，胡 瑞，鲍庆勇.高温环境对振动测试信号传输参数的影响［J］.航空动力学报，2009，8（08）：79-80.