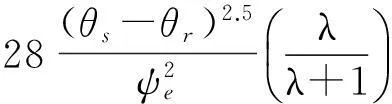Mualem模型中的饱和导水率修正研究
张 昊, 顾强康, 张仁义
(空军工程大学 机场建筑工程系, 陕西 西安 710038)
Mualem模型中的饱和导水率修正研究
张 昊, 顾强康, 张仁义
(空军工程大学 机场建筑工程系, 陕西 西安 710038)
摘要:[目的] 提高Mualem模型计算非饱和导水率的准确性。 [方法] 采用理论推导结合数据统计的方法研究该模型中的饱和导水率kspan修正问题。基于Brooks—Corey土壤水分特征曲线模型,建立修正导水率kspan与土壤水分特征曲线之间的理论关系式;通过回归分析得到kspan与土壤水分特征曲线之间的理论关系式中相关参数。 [结果] 利用原状黄土的非饱和渗透试验数据,对考虑修正导水率kspan的Mualem模型的准确性进行了验证,得到了比较满意的结果。 [结论] 研究成果可用于依据土壤水分特征曲线直接确定非饱和土导水率,对非饱和导水率预测研究具有一定参考价值。
关键词:非饱和土; 非饱和导水率; Mualem模型; 饱和导水率; 修正导水率; 土壤水分特征曲线
非饱和导水率是非饱和土研究中的一项重要内容。由于基质吸力的存在,不能用常规的测定饱和导水率的试验方法来确定非饱和导水率,使得非饱和导水率的确定具有很大的难度[1]。通过土壤水分特征曲线来间接预测导水率的方法已得到广泛认可。
Mualem非饱和导水率模型[2]因形式简洁、适用性良好而被广泛应用于非饱和导水率间接测定。饱和导水率ks是模型的重要参数,Mualem认为在非饱和渗流中,孔隙完全饱和时的导水率等于饱和渗流中的导水率。然而,饱和渗流与非饱和渗流的机理并不完全相同。van Genuchten[3]认为饱和导水率ks主要反映外力引起水在土孔隙中的流动特性,而非饱和渗流主要是由土体内部吸力引起的;Hoffmann—Riem[4]也认为Mualem需要通过修正来提高非饱和导水率的计算准确度;Marcel[4]通过对235组土样分析,认为Mualem模型中饱和导水率ks应替换成修正导水率ko,并且ko比ks小一个数量级。
将饱和导水率ks用导水率ko来修正,可以提高Mualem模型的计算准确性。无法直接测定的修正导水率ko的取值则成为非饱和导水率间接测定研究中的重要问题。本文用理论推导结合数据统计的方法,探讨 Mualem模型中的饱和导水率ks的修正问题,尝试得到一个可以依据土壤水分特征曲线直接计算非饱和土导水率的Mualem修正模型。基于Brooks—Corey土壤水分特征曲线模型,首先建立修正导水率ko与土壤水分特征曲线之间的理论关系式,然后通过回归分析求解相关参数,最后利用原状黄土的非饱和渗透试验数据对研究结果进行验证。
1考虑修正导水率的Mualem模型
1.1修正导水率与土壤水分特征曲线之间关系的理论推导
非饱和导水率模型的计算式可写成如下形式:
k=k0kr
(1)
在Mualem模型中,ko无法直接测量,是一个与孔隙半径有关的参数。Mualem认为k0等于饱和导水率ks,而ks可通过试验直接测定。然而在该模型中,k0是非饱和导水率曲线上的一点,其产生机理与饱和导水率ks并不完全相同。van Genuchten认为k0不等于ks的原因是二者的驱动力不同;Marcel通过数据分析认为ks比k0大一个数量级。所以需要对Mualem模型中的饱和导水率ks加以修正。
土的孔隙是一个互相连通的随机系统,非饱和导水率表征水在孔隙的流动特性,Mualem方程、van Genuchten方程、Childs and Collis—George[5]方程都说明孔隙分布与非饱和导水率存在对应关系。Marshall[6],Toledo[7]和Xu[8]利用土体基于孔隙分形得出了相应的土壤水分特征曲线计算方程,说明土壤水分特征曲线能够间接表征孔隙分布情况。土体孔隙的大小可通过孔隙半径r表征。Mualem通过体积含水量定义孔隙的分布函数f(r):
(2)
则最小孔隙半径为Rmin的土体中,孔隙半径R以下的孔隙水的体积含水量可由f(r)的积分形式来表示,即:
(3)
式中:θr——残余体积含水量(cm3/cm3);Rmin——孔隙半径(m)。
当被水充满的最大孔隙半径等于土体最大孔隙半径Rmax时,土体处于饱和状态,即:
(4)
式中:θs——土体的饱和体积含水量(cm3/cm3)。
Yang—Lapalce在毛管模型中给出的半径r与对应的吸力:
(5)
式中:Ts——水的表面张力(kg/m);α——接触角(°)。
Brooks—Corey土壤水分特征曲线模型为:
(6)
式中:ψ——基质吸力(kPa);ψe——进气值(kPa);λ——孔隙尺寸分布指标。
Mualem认为孔隙在三维空间上的体积分布与二维空间上的面积分布相同,即在面积分布密度函数为体积分布密度函数f(r)。在图1所示的模型的基础上建立了非饱和土导水率理论公式。
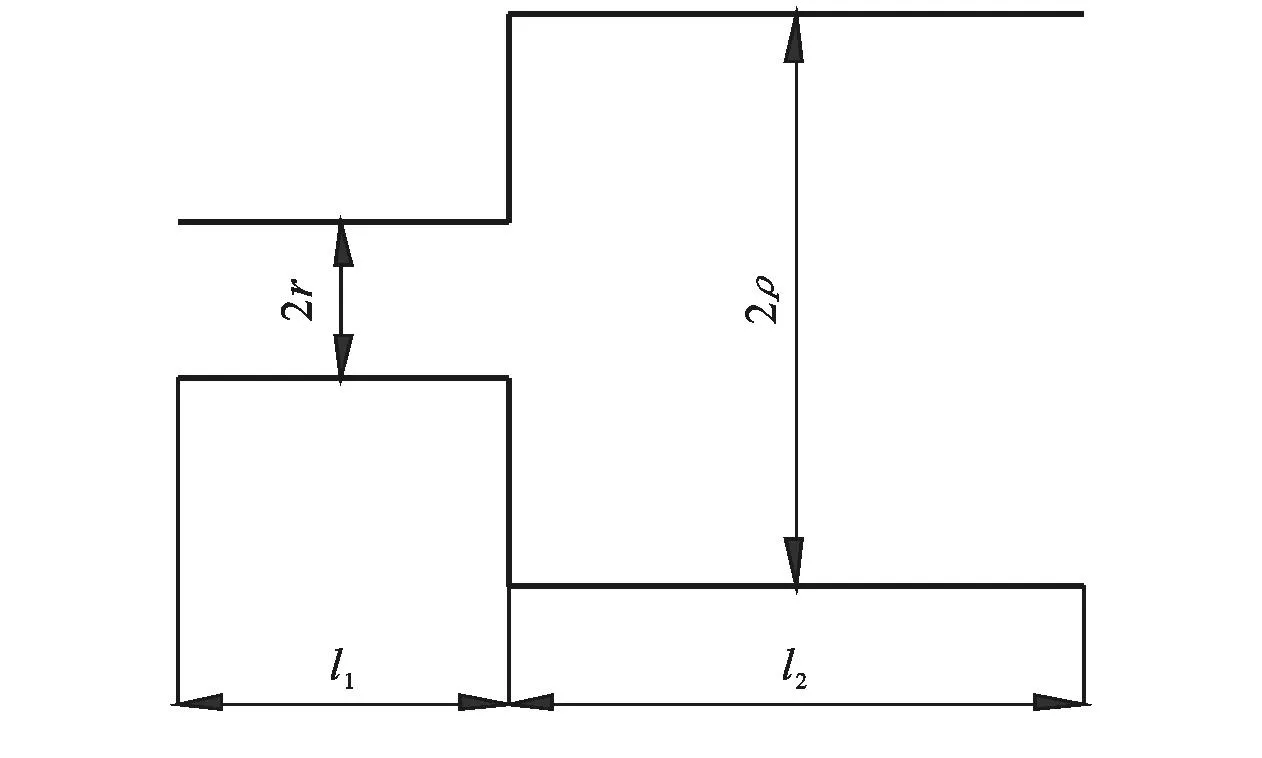
图1 Mualem双管联通模型
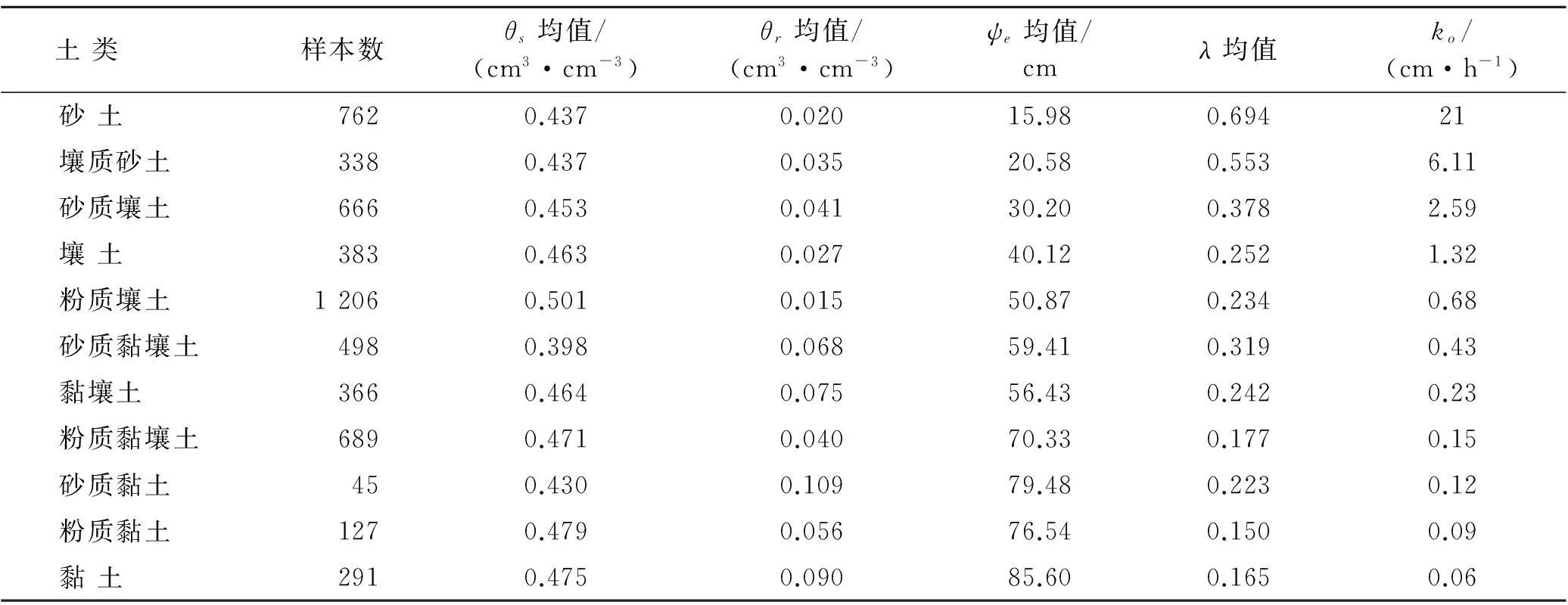
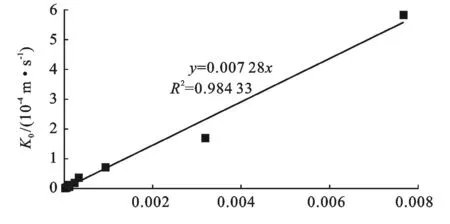
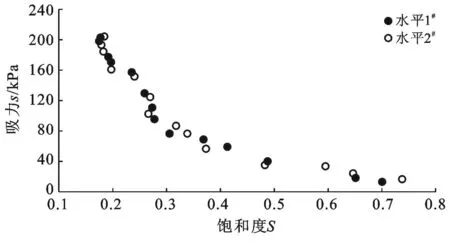
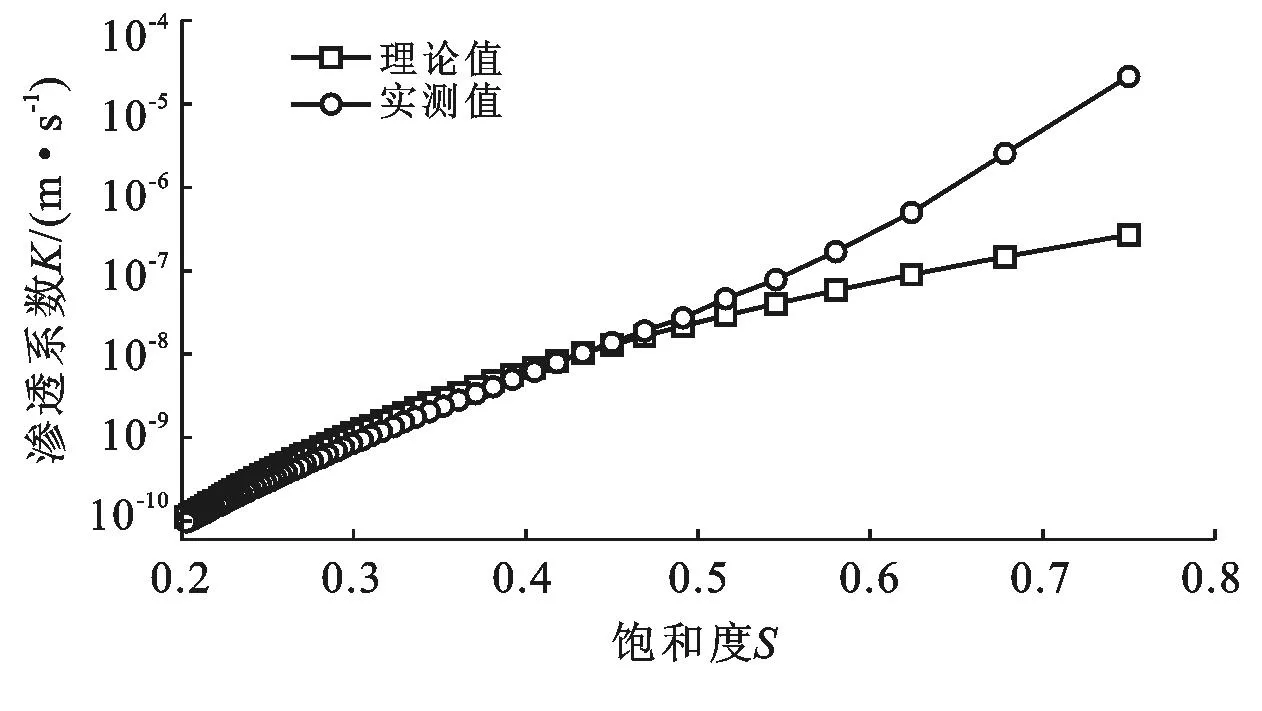
Mualem认为半径r和半径ρ孔隙联通的概率为rρf(r)f(ρ)。因为rρf(r)f(ρ)没有反映出水的渗流具有方向性,引入一个迂曲度因子T(0 (7) 将式(3)、式(5)和式(6)代入式(7),进行换元积分后有: (8) 故修正导水率k0为: (9) 参数M和T反映孔隙的形状,目前还没有有效的测试方法,Childs,Collis—George,Millington和Quirk[9],Burdine[10],Kunze[11]和Mualem都认为M与T的乘积与有效体积含水量呈幂指数关系,即: MT=B(θs-θr)l (10) 式中:B——常数。Childs和Collis—George认为l取0,Millington和Quirk认为l取4/3,Mualem认为l取0.5。将式(10)代入式(9),得: (11) 式中:A——常数,式(11)即为基于Brooks—Corey土壤水分特征曲线得到的修正导水率与土壤水分特征曲线理论关系。 常数A与孔隙形状、重力加速度、水的表面张力、浸润角、水的粘滞性有关。下面通过数据统计的方法对参数A的取值问题进行分析。Rawls依据粒径组成将5 371组土细分成11类[12],统计出了各类土Brooks—Corey土壤水分特征曲线参数平均值,并根据非饱和导水率曲线给出了相应的修正导水率(原文标注为饱和导水率),结果如表1所示。常数A的拟合结果如图2所示。将表1中的相关参数的单位换成常用单位,体积含水量的单位取cm3/cm3,进气值的单位取kPa,导水率的单位取m/s。理论关系式中参数的统计求解结果如图2所示。 表1 Rawls非饱和渗流参数统计结果 图2 Rawls非饱和渗流常数A的拟合 由图2可以看出,数据点分布在拟合直线附近,相关系数达到0.984。11类土的统计结果说明,修正导水率与土壤水分特征曲线参数之间呈现如式(11)所示的理论关系。拟合结果还说明,对不同的土类,式(11)中的参数A可以看成一个常数,其值可取0.007 28(m·kPa2)/s。 Mualem模型的修正导水率与土壤水分特征曲线参数之间的定量关系是: (12) 将Brooks—Corey土壤水分特征曲线模型带入Mualem模型得到的相对导水率kr为: (13) 式中:δ——经验常数,与孔隙尺寸分布指标λ有如下关系: (14) 将式(12)到(14)代入式(1),即得到考虑修正导水率k0的Mualem非饱和导水率模型: (15) 和原始模型比较,Mualem修正模型可以依据土壤水分特征曲线直接确定非饱和土导水率,并考虑了饱和导水率ks的修正。模型形式简洁,参数较少,是一个确定非饱和土导水率的简单方法。 2试验验证 姚志华[13]对兰州和平镇的原状黄土的土壤水分特征曲线和非饱和导水率进行了测定。试验采用2~3m之间的原状黄土,平均干密度1.28g/cm3,平均含水量6.2%,颗粒的相对密度2.71,液限平均值为28.7%,塑限为17.6%(以上指标均为2~3m之间均值)。土壤水分特性曲线的测定结果如图3。用Brooks—Corey模型对土壤水分特性曲线的结果进行拟合,结果如表2所示。本文用姚志华试验得到的非饱和渗流参数试验数据,对本文得出的Mualem修正模型进行检验。 利用式(15)计算得到的理论值与实测结果进行比较,结果示于图4。 原文是通过扩散率与容水率计算得到非饱和导水率,在计算扩散率过程中,对实测体积含水率曲线进行平滑修正[14],导致修正段前后一定范围内的导水率计算值偏离了真实值,修正段换算为饱和度正处于0.55到0.8区间内。图4显示在饱和度为0.8时非饱和导水率为2.10×10-5m/s,而姚志华实测得该土样的饱和导水率为2.76×10-6m/s,前者比后者大一个数量级。从图4可以看出,饱和度小于0.55段内,导水率理论曲线与试验点吻合度高,认为本文对Muale-m模型的修正结果合理。 图3 土壤水分特征曲线测定结果 θs/(cm3·cm-3)θr/(cm3·cm-3)ψe/kPaλR20.528011.470.5780.9943 图4 修正Mualem模型的验证 3结 论 饱和导水率ks影响Mualem模型计算准确性,用理论推导结合数据统计的方法对Mualem模型中的饱和导水率ks进行了修正。主要工作如下: (1) 将Mualem模型中的饱和导水率ks替换成修正导水率ko,基于Brooks—Corey土壤水分特征曲线模型,建立修正导水率ko与土壤水分特征曲线之间的理论关系式,用数据统计的方法求解理论关系式中的相关参数。得到一个可以通过土壤水分特征曲线直接确定非饱和土导水率的Mualem修正模型。 (2) 利用兰州和平镇的原状黄土的非饱和渗流参数试验数据对Mualem修正模型的准确性进行检验,试验值与理论曲线吻合性高,取得很好的检验结果。 (3) 用于对本文得到的Mualem修正模型的检验数据较少,研究成果的普遍适用性还需要进一步的研究。 [参考文献] [1]谢定义,陈正汉.非饱和土力学特性的理论与测试[C]∥土力学及基础工程学会.非饱和土理论与实践学术研讨会文集.北京:北京科技出版社,1992:227-229. [2]Mualem Y. A new model for predicting the hydraulic conductivity of unsaturated porous media[J]. Water Resources Research, 1976,12(3):513-522. [3]van Genuchten M T, Nielsen D R. On describing and predicting the hydraulic properties of unsaturated soils[J]. Ann. Geophys., 1985,3(5):615-628. [4]Schaap M G, Leij F J. Improved prediction of unsaturated hydraulic conductivity with the Mualem—van Genuchten model[J]. Soil Science Society of America Journal,2000,64(3):843-851. [5]Childs E C, Collis—George N. The permeability of porous materials[J]. Proceedings of the Royal Society of London(Series A): Mathematical and Physical Sciences, 1950,201,1066:392-405. [6]Marshall T J. A relation between permeability and size distribution of pores[J]. Journal of Soil Science, 1958,9(1): 1-8. [7]Toledo P G, Novy R A, Davis H T, et al. Hydraulic conductivity of porous media at low water content[J]. Soil Science Society of America Journal, 1990,54(3):673-679. [8]Xu Y. Calculation of unsaturated hydraulic conductivity using a fractal model for the pore-size distribution[J]. Computers and Geotechnics, 2004,31(7):549-557. [9]Millington R J, Quirk J P. Permeability of porous solids[J]. Trans. Faraday Soc., 1961,57:1200-1207. [10]Burdine N T. Relative permeability calculations from pore size distribution data[J]. Journal of Petroleum Technology, 1953,5(3):71-78. [11]Kunze R J, Uehara G, Graham K. Factors important in the calculation of hydraulic conductivity[J]. Soil Science Society of America Journal, 1968,32(6):760-765. [12]Rawls W J, Brakensiek D L. Prediction of soil water properties for hydrologic modeling[C]. ASCE, 1985. [13]姚志华,陈正汉,黄雪峰,等.非饱和原状和重塑Q3黄土渗水特性研究[J].岩土工程学报,2012,34(6):1020-1027. [14]雷志栋,杨诗秀,谢森传.土壤水动力学[M].北京:清华大学出版社,1988:21,92-94. Modification of Saturated Hydraulic Conductivity in Mualem Model ZHANG Hao, GU Qiangkang, ZHANG Renyi (DepartmentofAirportArchitecturalEngineering,AirForceEngineeringUniversity,Xi’an,Shaanxi710038,China) Abstract:[Objective] In order to improve the accuracy of saturated hydraulic conductivity in the Mualem model. [Methods] The modification of the saturated hydraulic conductivitykspanin the Mualem model was studied by theoretical method combined with data statistics. Based on the Brooks—Corey soil-water characteristic curve(SWCC) of unsaturated soil, a theoretical relationship between modified hydraulic conductivity and SWCC was presented, in which the correlation parameter was solved by regression analysis. [Results] Experimental data of undisturbed loess were used to evaluate the prediction outcomes of the Mualem model considering modified hydraulic conductivitykspan, which showed satisfactory result. [Conclusion] This theoretical model can be used to determine unsaturated hydraulic conductivity directly from SWCC, which possesses some references for further research on the prediction of unsaturated hydraulic conductivity. Keywords:unsaturated soils; unsaturated hydraulic conductivity; Mualem model; saturated hydraulic conductivity; modified hydraulic conductivity; soil-water characteristic curve 文献标识码:B 文章编号:1000-288X(2015)03-0168-04 中图分类号:TU43 收稿日期:2014-11-12修回日期:2014-12-02 资助项目:省部级项目“陕西延安机场工程” 第一作者:张昊(1991—),男(汉族),江苏省南京市人,硕士研究生,研究方向为地基处理与边坡稳定。E-mail:fourapril@sina.cn。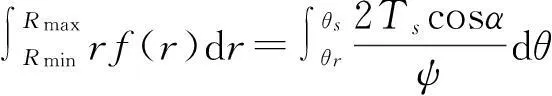
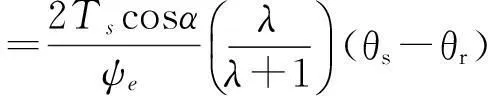
1.2 参数A的统计求解